构造概念格的权值优化改进算法*
朱文君, 王德兴, 袁红春
(上海海洋大学 信息学院,上海 201306)
构造概念格的权值优化改进算法*
朱文君, 王德兴, 袁红春
(上海海洋大学 信息学院,上海 201306)
针对基于信息熵与偏差的加权概念格在合并加权概念子格时,所得多属性内涵集权值较其整体在形式背景中的实际权重偏大,权重取值阈值的设置受主观因素干扰导致合并后的概念格规模过大的问题,提出了一种构造概念格的权值优化改进算法。以多属性内涵集在形式背景中的整体信息熵来设置其权值;采用方差计算各概念结点属性内涵集权值的阈值区间,克服了主观意识对阈值设置的影响;通过剪除不满足阈值区间的冗余概念结点,缩小了构造概念格的整体规模,减少了构造概念格的时间消耗。实验结果表明:对比基于信息熵与偏差的加权概念格减少了9.87 %的冗余结点,构造整体概念格的时间消耗减少了7.36 %,有效提高了加权概念格的构造效率。
形式背景; 概念格; 信息熵; 内涵权值; 阈值区间
0 引 言
数据挖掘和信息融合是数据处理与分析中不可或缺的主要处理过程,二者互相补充为用户提供准确有效的知识信息。文献[1]提出了基于数据挖掘技术建立信息融合模型的原理和算法,为两者相互结合有效地处理复杂数据的数据分析问题打下基础。文献[2]首次将概念格应用于数据融合领域,提出了基于概念格理论的数据融合处理机制。然而,随着形式背景的增长,概念格结点数指数级递增,合并分布存储的多个子背景效率变得越来越低,且极易生成过多冗余的信息,这些信息只会增加概念格内涵的比较次数,同时,影响概念格的构造效率。因此,减少适量冗余信息,提高概念格构造效率尤为重要。文献[3~5]提出了通过对属性的主观加权构造频繁加权概念格,使用户能快速地提取值得关注的知识。文献[6~8]在此基础上对构造主观加权概念格的时间复杂度进行了优化。但由于受到主观因素的影响,在专家经验不足时所赋权值偏差较大。文献[9]率先提出从客观角度采用信息熵对条件属性赋值,提高分类的效率。文献[10,11]对文献[9]进一步拓展,提出了一种基于信息熵与偏差的加权概念格内涵权重赋值方法,采用信息熵计算单属性内涵的权值,以其算数平均值表示多属性内涵集的权值,根据人工设定的偏差阈值删减概念结点。该算法在合并加权概念子格时,多属性内涵集权值较其在整体形式背景中的实际权值偏大,而且主观设置的阈值也导致了过多冗余概念结点的生成,构造概念格的规模过大,构造概念格的时间效率较低。文献[12,13]对概念格冗余属性的约简上做了研究,虽然减少了构造加权概念格的时间消耗,但对原始形式背景中包含的多属性内涵集的整体信息进行了删改,不利于用户提取准确有效的知识信息。
针对多属性内涵集的权值偏大及其阈值设置受主观因素干扰,使合并加权概念格的整体规模过大的问题,本文提出了以概念结点的多属性内涵集在原始形式背景中隐含的信息量的大小来设置其权值,不删改整体形式背景中的属性集,优化了构造概念格的属性内涵集权值。采用由方差计算的阈值区间来约束各概念结点属性内涵集的重要程度,通过删减不符合阈值区间的冗余结点,缩小了合并概念格的整体规模,提高了构造概念格的时间效率。
1 加权概念格
定义1 在形式概念分析中,加权形式背景定义为一个四元组Kω=(G,M,I,W),其中,G为对象集合,M为属性集合,I为G和M间的二元关系,W={w1,w2…wn},wi∈W(0≤wi≤1)为属性的权值[1]。对于一个对象x∈G,属性m∈M,那么xIm就表示对象x具有属性m。
定义2 三元组cω=(A,B,w),其中,A⊆G,B⊆M,w=w(B)∈[0,1],分别定义[1]如下两个映射:f(A)={m∈M|∀x∈A,xIm},g(B)={x∈G|∀m∈B,xIm}若两者之间满足A=g(B),B=f(A),则称三元组cw=(A,B,w)为一个加权概念,A,B分别是概念cw的对象和属性集合,w为权值。形式背景K中所有加权概念及其互相关系组成的集合称为加权概念格。
2 加权概念格的权值获取
2.1 属性内涵的权值获取
定义3 对于任意对象gi∈G,1≤i≤n,任意属性m∈M,则P(m/gi)表示对象为gi时具有属性m的概率,H(m)表示gi提供给属性m的平均信息量,即单属性m的权值wm为
(1)
定义4 若一个形式概念cω=(A,B,ω),且B={m1,m2,…,mn},Wqz(mi)=wi(i∈1,2,…,n),则多属性内涵集B的权值定义如下[8],其含义为多属性内涵集中各单属性权值的平均数,即
(2)
根据文献[10]获取属性内涵权值,一定程度上减少了属性内涵权重设置的主观性,然而,由单属性权值的平均数表示多属性内涵集的权值并未考虑多属性内涵重要性的总体水平,仅反映了各个单属性对多属性内涵集权值的贡献之和,因而,所得权值比多属性内涵集整体在形式背景中的实际权值偏大。
2.2 多属性内涵集权值优化改进
多属性内涵的权值计算方法不仅会影响加权概念格中的结点数目,也会影响其构造效率。当概念格结点内涵由多属性组成时,多属性整体的不确定性即为内涵集权值的不确定性,本文采用了多属性内涵整体的客观概率来量化其权值。而多属性内涵整体信息熵则作为其整体出现概率的度量由形式背景中各对象对多属性内涵集提供信息之和计算,进而以其整体信息熵来表示多属性内涵集的权值,更准确地反映了多属性内涵集的重要程度。
设在加权形式背景Kw=(G,M,I,W)下的一个加权概念cw=(Ai,Bj,w),对象集Aj={a1,a2,…,ai} A⊆G,多属性内涵集Bj={b1,b2,…bj} B⊆M,H(B)表示对象集合G提供给属性集Bj信息总量,多属性内涵集Bj的权值w(Bj)计算公式如下
(3)
(4)
式中 am∈Ai为对象集Ai的一个对象,n为概念结点数。当Ai=∅或Bj=∅,则w(Bj)=1。
2.3 多属性内涵集重要性阈值的优化
根据文献[10]基于信息熵与偏差的权值获取结果会与实际权值产生较大偏差,而人工设定的偏差阈值受主观经验的影响较大,这会导致提取到的信息难以被采纳。因此,本文提出区间阈值对权值设置约束,当计算所获权值不在阈值区间内时,则认为此概念结点是冗余的,从而使得冗余的信息不被用户提取。
本文用区间α=[μ-θδ,μ+θδ]表示内涵重要性的阈值区间,其中,μ为多属性内涵集内各单属性权值的算术平均值,δ为其方差,θ为内涵集权值偏差的约束。θ的取值通过最小化方差和的方法来获取。作为测算数值型数据离散程度的重要方法,方差是各变量值与其均值离差平方的平均数。方差和越大,则形式背景中各个概念结点的权值波动性越大,权值获取存在的偏差越大。方差和的最小化即可获取离散分布的属性权值的合理分布范围,使冗余的概念结点权值不落在阈值区间内,对该结点进行删减进而提高知识提取的准确性。
通过上述分析可以发现,因子表法在形成和应用因子表的过程中并没有考虑方程组元素本身的对称性。如果考虑这种对称性,则求解A(n-1)′阵时所采用的方式、求取A(n-1)′阵中元素的方式、对后续F阵元素的前代方式等,都将是简化因子表法的形成过程以及提高因子表法计算速度的关键。

(5)
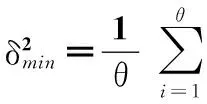
(6)
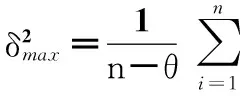
(7)
α=[μ-θδ,μ+θδ]
(8)
该算法无须调整任何参数,通过信息熵的分布生成,因此,具有较好的适应性。
2.4 算法分析
算法根据重要性阈值区间判断概念结点是否会被删除。对于符合阈值约束的结点予以保留并递归遍历其父结点集和子结点集,如此循环直至添加所有数据。对于一个概念结点C(x,k,w),至多存在2k个内涵包含于k的子概念。因此,在概念格的渐进式构造过程中,当所有结点都符合阈值区间,构造一般概念格的Godin算法时间复杂度[5]为O(2k|n|)(|n|为已有的结点个数)。而当加权概念结点被判断为冗余结点需要被删除时,在概念格的构造过程中将不生成该结点,相应的时间复杂度就会降低。由此,可得本算法的时间复杂度小于O(2k|n|),提高了概念格的构造效率。
3 实验和分析
数据来源于《上海海洋大学2009~2013年毕业生就业信息数据库》,对数据集进行预处理后构成形式背景,其M={a,b,c,d,e}属性集分别代表5个属性,应届生、计算机类择业倾向、英语六级、英语四级及中级口译。对象集G={1,2,3,4,5,6}为6位学生。
实验一:本算法与文献[10]算法分别构造加权概念格,比对其删除合并子格时所生成冗余结点的有效性。
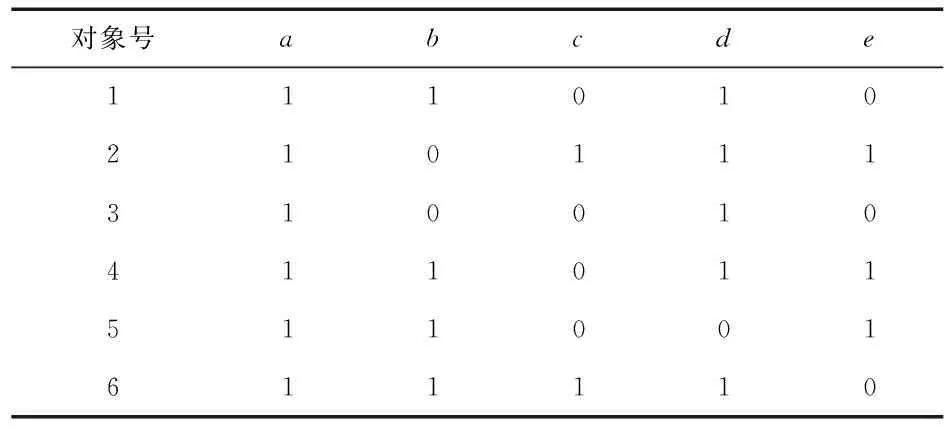
表1 合并形式背景
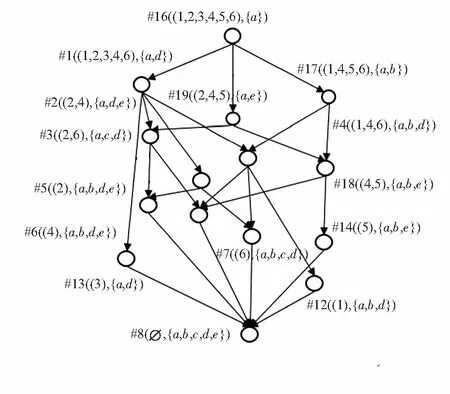
图1 合并概念格
2)表2所示为在未知多属性内涵集M中各单属性内涵重要性的情况下,利用信息熵客观获取单属性的权值,W={0,0.24,0.32,0.13,0.31}。
3)经计算求得θ=4,格结点多属性内涵集权值weight(B)及阈值区间如表3所示。
4)未能落在阈值区间内结点#1,#5,#6,#7,#13,#14,#18将被筛除,获得优化加权概念格如图2所示。
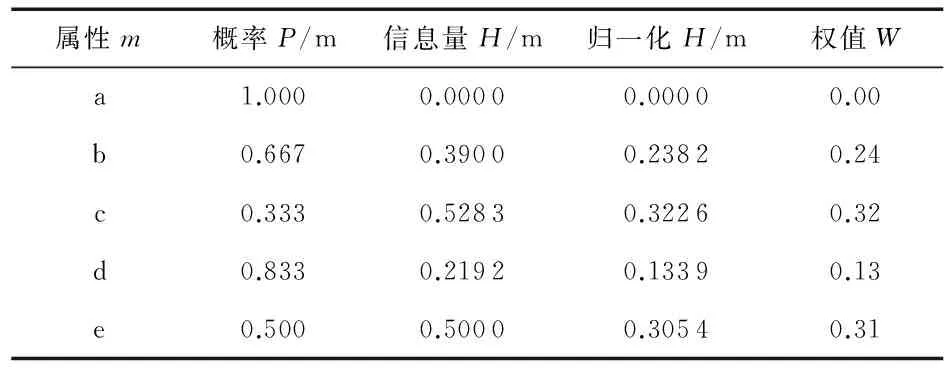
表2 单属性内涵权值

表3 多属性内涵集权值及阈值区间
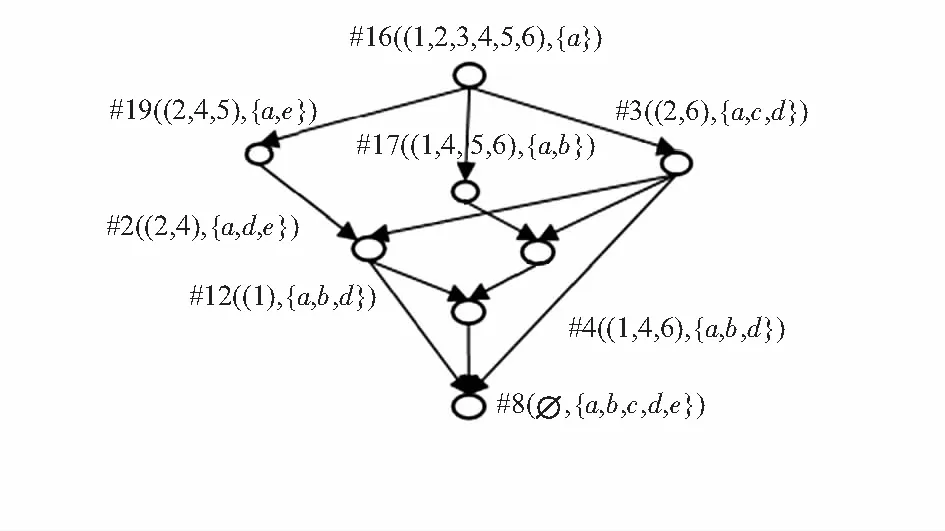
图2 优化加权概念格
对比采用文献[10]中权值获取的方法对多属性内涵集重要性赋值并构造加权概念格。
1)根据文献[10]获取多属性内涵集的权值weight(B)及其标准偏差D(B)如表4所示。

表4 多属性内涵集权值及偏差
2)设定内涵重要性阈值α=0.15,重要性偏差阈值β=0.18,删除冗余结点#1,#13,#19,#17,#2,#4,#12。
图3中删除的结点#1,#13反映了仅通过四级或中级口译认证的应届毕业生的并不是值得关注的人才,这不仅与文献[10]的算法所得结论一致也与现实背景相符。删除结点#5,#6,#7实现了英语水平有重叠的结点删减。对比文献[10]的加权方式,此类信息被冗余在了概念格中。#14,#18结点删除的意义是忽略有计算机类择业倾向的通过中级口译的应届生,作为一门地方培养项目的英语水平认证考试有其地方局限性,其含金量确实不高。对比文献[10]的加权赋值结果,结点#4的删除显然偏差较大,通过最基本的英语四级还是值得关注的。由此可以看出,在形式背景属性集权值并不清晰的情况下,本算法通过信息熵对属性内涵集重要性及其阈值区间做出客观评估可以更有效地提取出值得用户关心的信息。
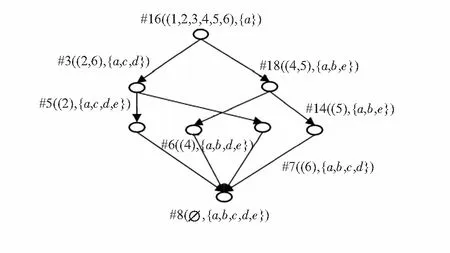
图3 对比加权概念格
实验二:在内存为2GB,操作系统为Windows XP的计算机上,在VC6.0的环境下,用C++语言实现了本文算法、文献[10]算法及 Godin算法[1]。选用2013届信息学院毕业生就业信息数据集进行实验,该数据集共有236条学生记录,38项相关属性,通过预处理后构成整体形式背景,以50条学生记录为单位将其划分为5个子形式背景。
将5个子形式背景依次进行合并,分别采用本算法、文献[10]算法及Godin算法构造合并后的整体概念格,对比其时间效率。三种算法构造概念格的执行效率对比结果如表5。
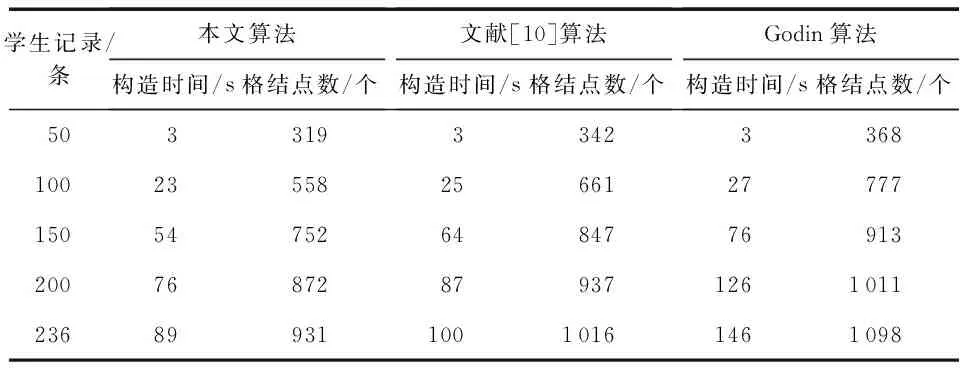
表5 三种算法执行效率对比
由实验结果可知,随着子形式背景依次合并,学生记录数逐渐递增,概念格中的概念结点数随之递增,概念格的构造时间也逐渐递增。由于Godin算法在构造概念格的过程中遍历了所有概念结点,因此其构造时间最长,执行效率最低。而文献[10]算法对部分冗余信息进行了删减,但其构造的概念格规模仍然较为复杂,仅减少了8.71 %冗余结点,构造效率较Godin算法提高程度有限,时间消耗缩短了17.13 %。与前两种算法相比,本算法构造概念格消耗的时间最短,时间消耗较文献[10]算法缩短了7.36 %,较Godin算法缩短了24.49 %,概念格的构造效率得到了显著的提高。此外,本算法较文献[10]算法进一步剪除了过量的冗余概念,构造概念格时生成的格结点个数减少了9.87 %,冗余结点得到了有效的删减,优化了概念格的整体结构,更有利于提取用户关心的知识信息。
4 结束语
本文在多个加权子格合并而专家或用户对新增对象缺乏了解时,首先以形式背景对多属性内涵集整体的信息量作为多属性内涵集的权重取值依据,解决了多属性内涵集权值较实际情况偏大的问题。其次,基于信息熵的分布由方差计算其阈值区间对多属性内涵集权值的最大及最小取值进行合理的约束。最后通过真实数据集验证了构造概念格的权值优化改进算法有效地优化了构造概念格的权值。通过对过量冗余概念结点进行删减,缩小了概念格的整体规模,从而提高了概念格的构造效率。
[1] 付 华,王雨虹.基于数据挖掘的瓦斯灾害信息融合模型的研究[J].传感器与微系统,2008,27(1):52-54.
[2] 吴桂清,胡 弦,张利民,等.捣固车作业系统异质多传感器数据融合的研究[J].传感器与微系统,2012,31(8):76-78.
[3] 张继福,张素兰,郑 链.加权概念格及其渐进式构造[J].计算机学报,2005,18(2):171-176.
[4] 张素兰,张继福,高愫邡.加权概念格的渐进式构造及其关联规则提取[J].计算机工程与应用,2005,41(7):173-175,178.
[5] 孙桂利,张继福.一种基于加权概念格的分类规则提取算法[J].太原科技大学学报,2011,32(5):352-357.
[6] 王欣欣,张继福,张素兰.一种频繁加权概念格的批处理构造算法[J].模式识别与人工智能,2010,23(5):678-685.
[7] 马 洋,张继福,张素兰.基于剪枝的约束概念格的渐进式构造算法[J].计算机应用,2009,29(5):1397-1400.
[8] 翟 悦,郭 杨,王玉姣.一种利用差集的加权频繁项集挖掘算法[J].辽宁工程技术大学学报:自然科学版,2016,35(3):312-317.
[9] 房鹏杰,张素兰,张继福.基于概念格和条件信息熵的分类规则获取方法[J].计算机工程与应用,2010,46(14):148-151,186.
[10] 张继福,张素兰,郑 链.基于信息熵和偏差的加权概念格内涵权值获取[J].北京理工大学学报,2011,31(1):59-63.
[11] Zhang Sulan,Guo Ping,Zhang Jifu,et al.A completeness analysis of frequent weighted concept lattices and their algebraic properties[J].Data & Knowledge Engineering,2012,11(2):246-267.
[12] 谢春丽,刘永阔.概念格理论属性约简算法研究[J].传感器与微系统,2012,31(3):116-118.
[13] 阎红灿,张 奉,王 云,等.基于粒计算的多值属性概念格约简[J].计算机应用,2015(A02):73-76.
Improved optimization algorithm of weighted concept lattice*
ZHU Wen-jun, WANG De-xing, YUAN Hong-chun
(College of Information Technology,Shanghai Ocean University,Shanghai 201306,China)
Since the multiple attribute intent weight values are slightly bigger than the actual weighted values when weighted concept sub-lattices based on information entropy and deviance being combined,thresholds disturbed by subjective factor directly causes the merged concept lattice size to be exaggerated,an improved optimization algorithm of weighted concept lattices is proposed.Multiple attribute intent weight values are decided by the whole entropy of attributes sets in data sets.Threshold interval of each concept node multiple attribute intent weight value is computed by variance to overcome the subjective factors.The size of the weighted concept lattice construction and time-consuming are reduced by removing redundant nodes which does not satisfy the threshold interval. The experimental results indicate that the proposed algorithm is reduced 9.87 % redundant nodes,the time-consuming of whole concept lattice construction is decreased by 7.36 %.The proposed algorithm apparently improves the efficiency of constructing weighted concept lattices.
formal context; concept lattice; information entropy; intent value; threshold interval
10.13873/J.1000—9787(2017)04—0153—03
2016—06—21
上海市科委科技支撑计划资助项目(14391901400)
TP 311
A
1000—9787(2017)04—0153—04
朱文君(1991-),女,通讯作者, 硕士,主要研究方向为数据挖掘,E—mail:zwj0956104@163.com。
袁红春(1971-),男,博士,教授,主要从事人工神经网络、智能计算工作。

