修正的UKF滤波时差定位算法*

刘 恋， 向凤红， 毛剑琳

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

修正的UKF滤波时差定位算法*

刘 恋， 向凤红， 毛剑琳

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

为了降低到达时间差(TDOA)测距在非视距(NLOS)传播环境中的误差，提出了在强跟踪无迹卡尔曼滤波(UKF)基础上改进的算法。在状态发生突变时，给预测协方差矩阵加入次优渐消因子；对NLOS误差进行正负判断，利用整体偏移法修改滤波增益，但估计协方差矩阵不做改进，以免出现不收敛。实验结果表明：该算法不仅能有效地抑制突变带来的影响，也能高效地消除NLOS误差，提高了NLOS传播的到达时间差定位精度。

到达时间差； 无线传感器网络； 非视距传播； 无迹卡尔曼滤波； 滤波增益

0 引 言

随着全球不同地区和用户应用的网络不同，尤其是GSM/GPRS/EDGEUMTS、CDMA2000、PHS、WLAN和WiMAX等无线网络技术互补融合，无线异构网络受到广泛关注[1]。与在同构网络中的定位技术一样，异构无线传感器网络，很多功能的实现都依赖网络定位技术的精度。

到达时间差(time difference of arrival,TDOA)[2]定位技术是无线传感器网络节点定位的一种重要技术，它具有精度高、易组网实现、能对付宽带低谱密度信号等优点。TDOA技术是测量移动台(mobile station,MS)到不同基站(base station,BS)的时间差而进行估计MS的位置。由于无线电信号在实际传输过程中易被障碍物遮挡只能以反射、折射等非视距(non line of sight,NLOS)传播方式进行传播，因此,MS位置估计问题就转化成高度非线性方程组估计问题。

在引入了NLOS误差的TDOA定位中，扩展卡尔曼滤波(extended Kalman filtering,EKF)[3,4]被广泛应用，它对非线性模型进行一阶Taylor展开，缺点是近似线性化在对状态后验分布的估计中引入很大误差。所以，学者们提出了一种确定性样本点计算的滤波算法无迹卡尔曼滤波(unscented Kalman filtering,UKF)[5]，它直接利用真实的系统模型，其后验值和协方差可以精确到三阶Taylor展开，但它的缺点是在模型不准确或状态发生突变的情况下鲁棒性不佳。在文献[6]中,提出先对系统状态进行突变判断，状态发生突变时给预测协方差矩阵加入多重次优渐消因子，以消除状态突变时的影响,虽然这种方法明显优于标准UKF,但它仅改进了异常状态的部分误差，在状态正常时对引入NLOS误差却不能很好地消除。针对这个问题，本文将基于改进的强跟踪UKF算法引入到TDOA抗NLOS的处理中，并对此进行改进，避免原文中的算法对引入NLOS误差可能出现的不收敛问题，提高了系统的自适应能力和鲁棒性。仿真结果验证了所提算法的有效性。

1 时差定位数学模型

假设在二维空间中有M个基站，基于时差定位的空间示意图如图1所示。图中，u=[x,y]T为MS待估计位置坐标；si=[xi,yi]T为第i个BS的实际位置坐标。MS到BSi之间的距离为

(1)

式中 ‖‖为模。

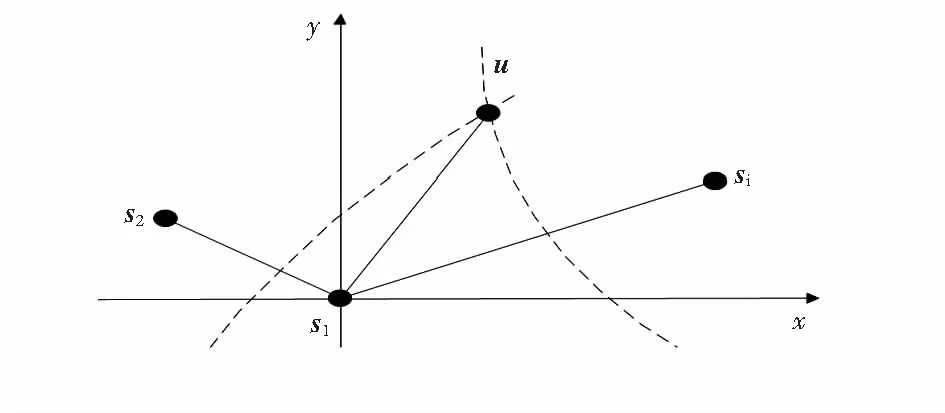
图1 时差定位原理图

ti为电信号从MS到BSi的视距(lineofsight,LOS)传播时间，tei为从MS到BSi的NLOS超量时延，它为一个正值的随机变量，各tei之间相互独立，当电信号从MS到BSi的是LOS传播时,tei=0。不失一般性，选取s1作为参考接收站，可以得到MS到BSi的TDOA定位方程为

i=2,…,M

(2)

i=2,…,M

(3)

r=f(u)+η

(4)

式中r=[r21,…,rM1]T；f(u)=[f21(u),…,fM1(u)]T；η=[η21,…,ηM1]T，为方便起见，认为此噪声η服从均值为零、正定协方差矩阵为Q的高斯分布

Q=E[η-E[η])(η-E[η])T]

(5)

式中 E[]为期望值。根据式(4)可得似然函数[6]为

exp{-(1/2)(r-f(u))TQ-1(r-f(u))}

(6)

式中 Q-1为Q的逆矩阵，Q为对称正定矩阵，其逆存在。

最大似然估计是最大化(6)中u的值，因此,可以转化为最小化二次型目标函数，即

J(u)=(r-f(u))TQ-1(r-f(u))

(7)

根据式(7)可知，求解u必须求J(u)的最小值，但是用解析方法求解高度非线性函数非常困难[8]。因此，本文采用最优估计求解此非线性方程，确定MS的位置坐标值。

2 基于修正UKF的时差定位算法

2.1 标准UKF算法

由于式(3)为高度非线性函数，得到的式(7)的几何结构很不规则，且存在局部极小点[9]。而滤波主要解决以某种最优方式联合求解未知方程和测量方程的问题，因此，先将时差定位问题转化成非线性系统方程，建立状态方程和测量方程

(8)

式中sk和zk分别为第k个时刻的状态向量和测量向量，Fk和Hk分别为状态转移矩阵和测量矩阵,wk和vk分别为第k个时刻的过程噪声向量和测量噪声向量，其统计特性满足

(9)

式中Qk和Rk分别为wk和vk的协方差矩阵，δkj为Kronecker-δ函数。UKF的算法过程如下：

1)滤波初值

(10)

2)样本点计算

(11)

式中a∈R为调节参数，取值为一个小的正值。

3)时间更新

(12)

(13)

(14)

4)量测更新

(15)

(16)

(17)

(18)

式中 Kk为第k个时刻的滤波增益，Rk为vk的协方差矩阵,ek为zk所对应的新息过程。

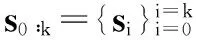
pk=p(s0∶k,z1∶k)

(19)

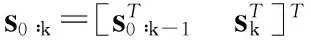
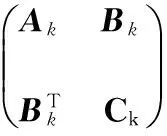
(20)

(21)

(22)

(23)

式中n=1,2,…,nx，sk[n]为状态矢量sk的第n维。

从上述过程式(12)～式(18)可看出，状态的每一次更新都是由前一次状态估计和新的变量测量值得到，而且Kk是估计值随新息过程值变化程度的标志。因此，可通过改变增益Kk的大小来控制估计值。第一，在状态突变时不受上次修正Kk影响的情况下将次优渐消因子引入到预测协方差矩阵P～k中。第二，利用整体偏移法[10]直接修正增益。这样可以实时调整滤波增益Kk，提高系统的鲁棒性。

2.2 修正UKF算法

2.2.1 强跟踪UKF算法

在式(16)中可知滤波器输出的新息序列为ek，衡量滤波性能优良时它应满足

(24)

此式要求不同时刻的新息向量保持正交关系，且具有类似白噪声的性质，表明已将新息序列中的一切有效信息提取出来。

利用新息序列的统计信息，采用假设检验的方法对系统异常进行检测，定义统计量

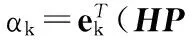
(25)

统计量αk服从自由度为m的χ2分布。判断状态是否突变

(26)

若检测到状态突变，给预测协方差矩阵P～k引入次优渐消因子λk，则

(27)

(28)

令Vj=0，由式(15)与式(28)可得

(29)

令λk=diag(λ1,k,λ2,k,…,λn,k)，对式(27)与式(29)求迹可得解

(30)

(31)

状态突变时，式(15)改变如下

(32)

2.2.2 修正滤波增益

由第1节可知，NLOS传播给TDOA测量引入的误差tei1是两个随机变量之差，其值与MS到BSi的距离有关。而在式(17)中新息ek代表预测值往估计值校正的方向和大小。因此，可以根据ek的大小和引入误差是正还是负，改变式(17)中Kk大小，使偏离的估计值拉回到正确的方向。

增益Kk修正情况如下

(33)

式中 “+”代表正偏时的情况，“-”代表负偏时的情况；θ≥1为可调修正因子，其根据实验统计取值。

式(17)则作出如下修改

(34)

2.2.3 修正UKF算法实现

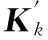
1)采用式(10)进行初始化；

2)利用式(11)进行样点计算；

3)采用式(12),式(13)计算状态预测；

4)采用式(26)的方法对状态突变做出预判，若存在突变, 则用式(27)计算P～k，式(32)代替(15)计算Kk，否则，采用式(13)计算P～k；

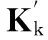
6)完成剩下的时间和量测更新，返回步骤(2)，进行下一次滤波解算。

3 仿真实验与分析

在一片区域内，将4个传感器节点按设定位置部署。设主节点位置s1为(0,0)，3个辅节点位置为s2(100,400),s3(800,400),s4(800,0)。辐射源沿着运动轨迹(见图2)运动：依次以1m/s从A,B,C到D。在B点有一次状态突变，运动曲线AB到BC的斜率由4/3转变为3/4；在C点也发生了一次状态突变，运动曲线BC到CD的斜率由3/4转变为-4/3。从A运动到B，需要100s，共100m；从B运动到C，需要600s，共600m；从C运动到D，需要500s，共500m。

图2 运动轨迹

仿真时，每秒测量一次TDOA值，仿真时间为1 200s，每次实验中共有1 200个TDOA测量值。NLOS传播分3种情况：1)主节点与辐射源是LOS传播，辅节点与辐射源是NLOS传播，仿真时由经验值选取θ=5，E=1μs，TDOA重构误差仿真结果见图3；2)主节点与辐射源是NLOS传播，辅节点与辐射源是LOS传播，仿真时由经验值选取θ=3,E=1μs，TDOA重构误差仿真结果见图4；3)辐射与主节点辅节点间都是NLOS传播，仿真时由经验值选取θ=2,E=1μs，TDOA重构误差仿真结果见图5。

图3 NLOS只影响主节点

图4 NLOS只影响辅节点

图5 主节点和辅节点都受NLOS影响的仿真结果

仿真结果如图3、图4和图5所示，将标准UKF算法、强跟踪改进UKF算法和本文算法进行测量值重构TDOA误差进行仿真。在0s开始时，辐射源从A出发，由于本文算法中先对NLOS误差进行判决，用整体偏移法修正了滤波增益，所以,本文算法在开始时误差就比其他两者小。在0～100s阶段，辐射源从A运动到B，3种算法的TDOA误差都是由大到小，这是因为随着迭代次数逐渐增加误差减小；在100～200s，辐射源从B点出发，在B点有一次突变，所以TDOA误差都有一定的波动；在700～810s时，辐射源从C点出发，在C点有一次突变，这次突变比B点突变对系统影响大，这是因为在此点突变比B点大。在1 000s以后，在C点突变影响结束后，随着迭代次数的增加，TDOA误差趋于稳定。在整个过程中，强跟踪改进UKF算法比UKF误差相对低，是因为强跟踪UKF算法在面对突变时加入了次优渐消因子，在以后的迭代也起了相应的作用，但在图4中出现超调现象，所以，在此基础上本文算法不仅使此次迭代不受上次修正的预测方差矩阵影响，而且修正了滤波增益。因此,在图3、图4和图5中，本文算法比其他2种算法，TDOA误差明显小，而且在面对突变时，本文算法虽有一点波动，但相较于其他2种算法，波动较小。

比较仿真结果图3、图4和图5，会发现主节点和辅节点只有一个受NLOS影响比两者都受影响时，UKF和强跟踪改进UKF算法的TDOA误差更大，这是因为在两者都受影响时，NLOS误差做差抵消了一部分NLOS影响。本文的算法在这3种情况下，TDOA误差都比较小，这是因为在计算过程中根据NLOS误差的正负对增益Kk进行了修正，有效地减少了NLOS误差。

根据式(23)分别对情况一、二、三进行了200次蒙特卡洛实验，并计算得到TDOA估计值的RMSE，其值见表1。

表1 3种情况下TDOA估计值的RMSE

由表1可看出，本文算法比另2种算法明显削弱了NLOS和突变对TDOA定位的影响，显著提高了定位精度。

4 结束语

本文提出了在强跟踪UKF的基础上减小NLOS对系统的影响的算法。利用新息序列判断状态是否突变，若突变则将次优渐消因子引入预测协方差矩阵中，使状态突变对系统的误差减小；判断出NLOS误差正负，对TDOA重构，进行滤波增益的修正。仿真结果表明：经过改进后的算法，在状态突变时，不仅没有增加计算的复杂度，也大大减小了NLOS对定位的影响，提高了定位精度，并且改善了系统不收敛的现象。另外，如何将此方法运用到不同模型中，也是将继续研究的内容。

[1] 杜晓玉,孙力娟,郭 剑,等.异构无线传感器网络覆盖优化算法[J].电子与信息学报,2014(3):696-702.

[2] 高洪元,于雪梅,赵忠凯.基于文化鱼群算法的到达时间差定位技术[J].计算机工程,2011,37(14):137-139.

[3] 罗 磊,田增山,陈俊亚.EKF定位跟踪算法研究[J].重庆邮电大学学报:自然科学版,2009,21(1):50-52.

[4] 李仕云，邓洪权.基于EKF的双站测向/时差联合定位算法[J].无线通信技术，2015，41(1)：38-40.

[5] 姚依翔,谢俊元.基于UKF区域交叉定位的WSNs Sink节点动态跟踪算法[J].传感器与微系统,2015,34(4):123-126.

[6] 胡高歌,刘逸涵,高社生,等.改进的强跟踪UKF算法及其在INS/GPS组合导航中的应用[J].中国惯性技术学报,2014,22(5):634-639.

[7] Torrieri D J. Statistical theory of passive location systems[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(2):183-198.

[8] 朱国辉,冯大政,李 进,等.一种利用修正牛顿迭代的时差定位算法[J].西安电子科技大学学报：自然科学版,2014,41(5):36-41.

[9] Dogancay K,Sakhtsari A H.Target tracking by time of difference of arrival using recursive smoothing[J].Signal Processing,2005,85(4):667-679.

[10] 李 静,刘 琚.用卡尔曼滤波器消除TOA中NLOS误差的三种方法[J].通信学报,2005,26(1):130-135.

[11] 薛 丽,高社生,胡高歌.自适应Sage-Husa粒子滤波及其在组合导航中的应用[J].中国惯性技术学报,2013,21(1):84-88.

Modified UKF filtering time difference localization algorithm*

LIU Lian, XIANG Feng-hong, MAO Jian-lin

(Faculty of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650000，China)

In order to reduce time difference of arrival(TDOA)ranging error in non line of sight(NLOS) environments,two improvements are introduced to enhance unscented Kalman filtering(UKF).When the system states change, suboptimal fading factors are added into the prediction covariance to eliminate the influence of mutational states.Secondly,judging type of NLOS error and using the total-deflection method can modify filtering gain,but estimation covariance matrix is not modified to avoid non-convergence.Experimental result indicates that the proposed method can not only restrain the influence of mutation,but also eliminate NLOS error highly effectively and improve positioning precision greatly.

time difference of arrival(TDOA); wireless sensor networks(WSNs); non line of sight(NLOS)propagation; unscented Kalman filtering(UKF); filtering gain

10.13873/J.1000—9787(2017)04—0138—05

2016—03—25

国家自然科学基金资助项目(61163051,F020809)

TN 923

A

1000—9787(2017)04—0138—05

刘 恋(1991-)，女，硕士研究生，主要研究方向为物联网、无线传感器网络定位。