拉压不同模量矩形板的双向弯曲问题

张良飞,姚文娟

(上海大学土木工程系,上海 200444)

拉压不同模量矩形板的双向弯曲问题

张良飞,姚文娟

(上海大学土木工程系,上海 200444)

拉压不同模量矩形板的双向弯曲的中性轴可以从两个弯曲方向考虑.基于不同模量理论,利用静力平衡方程推导了不同模量矩形板的中性轴位置,再利用Kantorovich变分法求解了不同模量矩形板的挠曲线方程,并将得到的数值解和有限元解进行比较,二者较为吻合.计算结果表明,当拉压不同模量的差异较大时,不同模量弯曲矩形板的挠度不宜采用相同模量经典板壳理论.该方法为分析不同模量矩形板和其他结构形式的板的弯曲问题提供了求解思路,并为其在工程中的应用提供了一定的理论参考.

Kantorovich变分法;不同模量;双向弯曲

工程上广泛应用的许多材料,如混凝土、金属、石墨、塑料、生物材料等都具有拉压不同模量特性,特别是近几年发展起来的复合材料以及聚合材料的不同模量之比高达4,其双模量特性所引发的力学性质差异已经到了不容忽视的程度.因此,由双模量材料制成的结构力学研究备受关注.最初的双模量问题的研究是由美国学者Jone[1]、Bert[2]及前苏联学者Ambartsumyan[3]提出,1986年Ambartsumyan[3]发表了拉压不同模量弹性问题的专著,总结了双模量的基本概念和基本假设,并提出了主应力的正负为拉压判定准则.

早期,对于有限元的研究还主要基于有限元数值的方法.Rafaele等[4]和Patel等[5]基于Bert[2]提出的双模量模型——以纤维的纵向应变的正负为拉压判定准则,分析了双模量层压复合板应力计变形;针对有限元方法迭代速度慢的问题,He等[6]应用了剪切模量法提高了计算速度;Yang等[7-8]用光滑技术处理双模量模型,避免了迭代中应力状态的判断从而简化了计算,并建立了初应力有限元及神经网络预测模型[8].

根据双模量材料特殊的非线性特点,Yao等利用流动坐标系统结合分段积分法推导了双模量弯压柱[9]、横力弯曲梁[10]、挡土墙的中性轴[11]、应力和位移的解析解;何晓婷等[12-13]采用简化等效刚度法对不同模量弯曲梁和柱进行了分析;Qu[14]通过引入Yao的等效弹性模量,推导了双模量土工格室变形表达式.

对于薄板弯曲问题,高潮等[15]基于不同弹性理论,采用有限元数值方法分析了弯曲板;吴晓等[16-17]用变分法研究了不同模量圆板和矩形板的弯曲问题,在研究过程中简化了对于中性轴位置确定的步骤,并假设双向弯曲截面上的中性轴在同一平面.实际上不同模量板双向弯曲时中性层不在同一平面上,且其位置的确定不仅依赖于结构材料,而且还与结构形状、边界条件、外荷载等有关,是诸多因素所致的具有非线性现象的力学问题,至今尚未有学者对此问题进行解析研究.本工作首先基于Ambartsumyan[3]的不同模量理论,利用静力平衡方程推导出不同模量弯曲板的中性轴方程,计算得到中性轴位置的数值解;接着用Kantorovich变分法研究了不同模量弯曲板变形问题;最后分析了拉压不同模量对四边固支矩形板弯曲变形的影响.

1 拉压不同模量弹性理论

1.1 基本概念和初始假设

在绝对值相同的拉应力和压应力的作用下,材料会发生绝对值不同的拉应变和压应变,即材料具有不同的拉伸弹性模量Et和压缩弹性模量Ec.在轴向应力作用下,材料在拉伸和压缩时的应力应变关系是非线性的.

假设所研究的物体是变形连续的固体,物质是均匀的、各向同性的,但由于主应力符号的不同而产生不同的弹性性质,即一维拉伸时所研究材料的任何方向有弹性模量Et,一维压缩时有Ec,材料在任意应力状态下只发生弹性小变形,并服从连续弹性介质的一般规律.经典弹性理论的基本方程和关系式保持不变,不同之处仅反映在物理方程(本构关系)中.

研究对象为薄板,以如下两个计算假定为基础:①垂直于中面方向的正应变εz可以不计;②应力分量τzx,τzy和σz远小于其他3个应力分量,其引起的形变可以不计.

1.2 应力应变关系

根据不同模量弹性理论,假定主应变和主应力分别为{σI}和{εI},在主方向上的本构关系为式中,[a]为柔度矩阵,是由主应力的符号确定;[D]为弹性矩阵,是由主应变的方向确定.且这些矩阵满足如下关系:

由不同模量弹性理论本构关系可知,对于平面问题,[D]和[a]的矩阵单元可以表示如下.

2 中性轴位置的确定

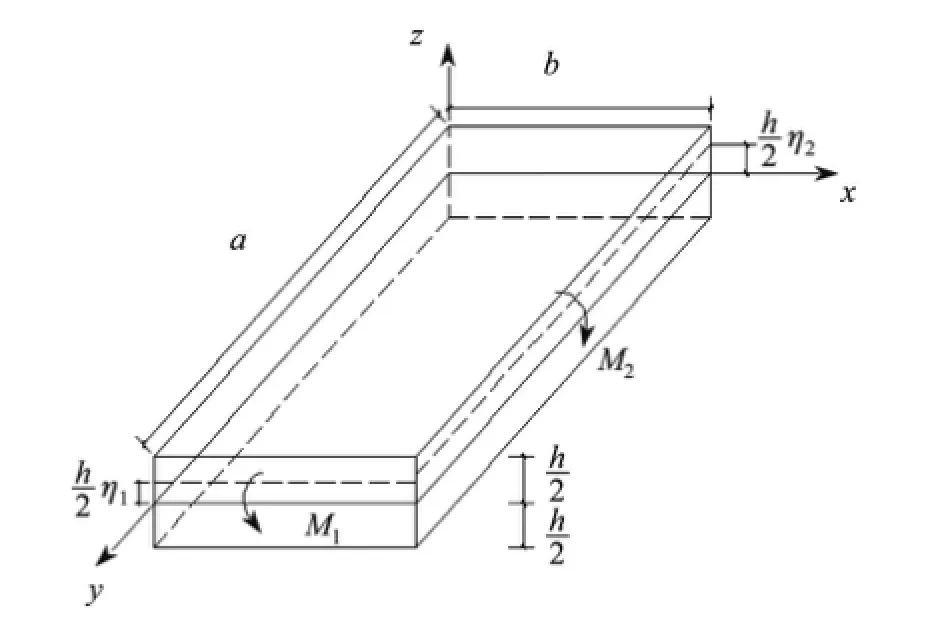
图1 计算模型Fig.1 Calculation model

由方程组(12)可知,不同模量薄板两弯曲截面应力改变符号的位置(由η1,η2决定)与拉压模量比、拉压泊松比、板边弯矩之比有关,方程组(12)是这些参量的非线性函数,为二阶非线性方程组,对其进行求解可以得到中性轴位置的数值解.

3不同模量弯曲薄板的Kantorovich变分解

利用微分符号和变分符号的可交换性,对式(19)分部积分得

4 算例和讨论

4.1 算例与计算结果

薄板尺寸为a=2 000 mm,b=1 000 mm,h=200 mm,受均布荷载q=2 MPa,M1= 20×106N·m,M2=5×106N·m.为了具体分析拉压弹性模量对矩形板弯曲变形的影响,取如下材料弹性模量计算:①保持E=(Ec+Et)/2=4 000 MPa不变,不同模量比Et/Ec在1.5～5.0范围内变化;②保持Ec=1 000 MPa不变,Et/Ec在1.5～5.0范围内变化.

分别采用本工作推求的不同模量薄板挠曲线公式以及不同模量有限元数值解对四边固支矩形薄板进行求解,并用经典板壳理论计算出同模量时板的挠度.有限元数值模拟用Ansys 12.0,采用8节点Solid185单元,利用小位移静力分析进行求解(部分结果见表1).

表1 不同模量矩形板中性轴位置、位移计算结果Table 1 Neutral axis location and displacement of rectangular plates with diferent modulus

4.2分析与讨论

运用本方法所推求的板中心处挠度与不同模量有限元模拟结果吻合较好(见表1及图2),其误差均在5%以内,验证了本方法的可靠性.

计入不同模量后,随着材料压、拉模量比Et/Ec的变化,算例中薄板的板中心挠度呈有规律的变化(见图2).当双模量的平均值E=(Et+Ec)/2保持不变,随着Et/Ec的增大,不同模量板中心挠度呈非线性增大:当Et/Ec从1.5增大到2.5时,相应的板中心挠度增大了4 mm;当Et/Ec从2.5增大到5.0时,板中心挠度增大了22 mm.如果Ec不变,当Et/Ec增大时,则板中心处的挠度呈非线性减小:当Et/Ec从1.5增大到3.5时,相应的板中心挠度减小21 mm;当Et/Ec从3.5增大到5.0时,板中心挠度减小3 mm.这说明当双模量的平均值E=(Et+Ec)/2保持不变时,随着Et的增大,则Ec减小,板整体刚度分配不均匀,导致板中心挠度增大;如果Ec不变,当Et/Ec增大时,板的整体模量增大,则板的挠度减小;但当Et/Ec继续增大时,拉、压模量的离散性在增大,即不均性在增大,因此板中心挠度曲线最终趋于平缓.

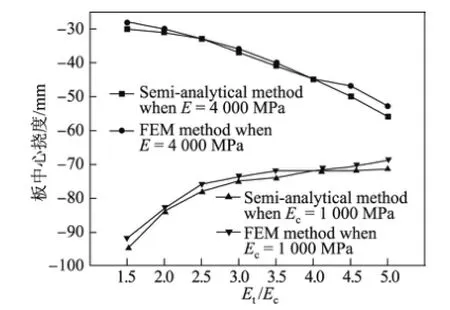
图2 E=4 000 MPa和Ec=1 000 MPa时利用本方法和有限元求解的板中心处挠度Fig.2 Finite element method solution and the proposed solution of displacement at the center of the plate when E=4 000 MPa and Ec=1 000 MPa

运用本方法算得的不同模量板的挠曲线和运用经典板壳理论算得的相同模量板挠曲线如图3和4所示.从图中可以看出,挠曲线沿板长边方向均呈抛物线形状.当E=(Et+Ec)/2不变时,随着Et/Ec增大,不同模量板的挠度均大于相同模量板的挠度,且板挠度呈非线性增大趋势,沿板边向板中心方向板的挠度在增大.当Ec不变时,随着Et/Ec增大,薄板的挠度非线性减小,不同模量板挠度均小于相同模量板的竖向位移,沿板中心向板边方向板的挠度在减小.

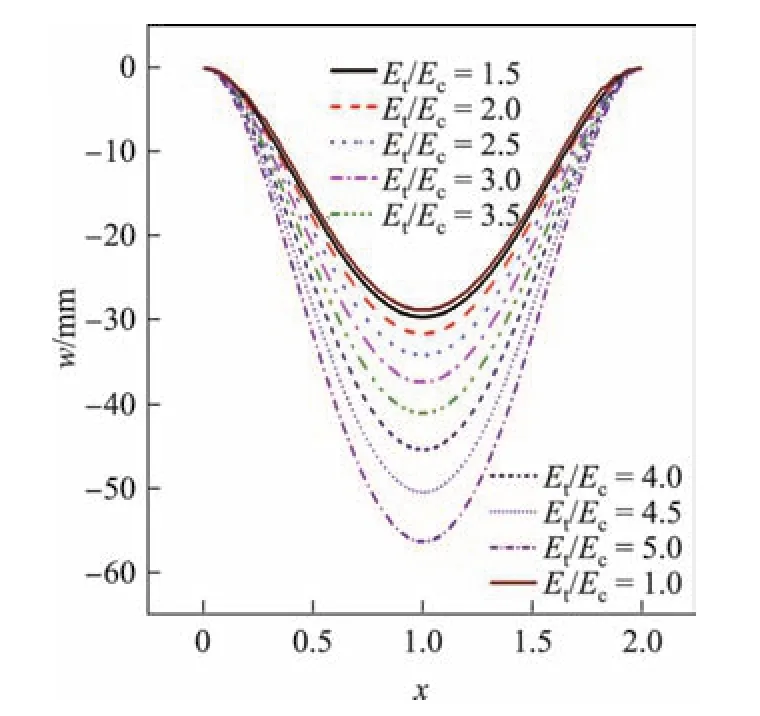
图3 E=4 000 MPa时板挠曲线Fig.3 Displacement curves when E=4 000 MPa

图4 Ec=1 000 MPa时板挠曲线Fig.4 Displacement curves when Ec=1 000 MPa

在本算例中,当Et/Ec=2.5时,保持E不变的不同模量板中心挠度为−34 mm,运用经典板壳理论算得相同模量板的中心挠度为−27.1 mm,二者之间相差达到25.5%,超过20%;当Ec不变,增大Et时亦如此,故此时不宜再按照相同模量经典理论计算.

5 结论

(1)在矩形薄板x和y方向作用有不同的弯矩时,薄板双向弯曲,中性层不在一个平面上.本工作将板沿板厚方向分3层(理论上分层越多,越接近真实受力状态),每一层默认为同一类应力区域,引入不同模量的本构关系,得到不同方向截面上的中性轴,用Kantorovich变分法计算出薄板的挠度曲线表达式.结果表明,这种近似计算的方法和不同模量有限元模拟方法较为吻合,二者误差小于5%.

(2)在保持E=(Et+Ec)/2和Ec不变的两种情况下,随着Et/Ec增大,板的挠度表现出不同的变化趋势,前者呈非线性增大趋势,后者减小后趋于平缓.

(3)在本算例中,当Et/Ec≥2.5时,运用经典板壳理论算得的板位移值和不同模量数值解之间相差超过20%,此时不宜按照相同模量经典理论计算,而应采用不同模量理论.

[1]JONE R M.Stress-strain relations for materials with diferent moduli in tension and compression[J].J AIAA,1977,15:16-23.

[2]BERTCW.Modelsforfbrouscompositeswithdiferentpropertiesintensionand compression[J].J Engg Math Tech(ASME),1977,99:344-349.

[3]AMBARTsuMYAN S A.Elasticity theory of diferent modulus[M].Beijing:China Railway Press, 1986.

[4]RAFFAELE Z,FABRIZIO G.Damage evolution in bimodular laminated composites under cyclic loading[J].Compo Struct,2001,53:381-402.

[5]PATEL B P,LELE A V,GANAPATHI M,et al.Thermo-fexural analysis of thick laminates of bimodulus composites materials[J].Compo Struct,2004,63:11-20.

[6]HE X T,ZHENG Z L,SuN J Y,et al.Convergence analysis of a fnite element method based on diferent moduli in tension and compression[J].Int J Solids Struct,2009,46:3734-3740.

[7]YANG H T,ZHu Y L.Solving elasticity problems with bi-modulus via a smoothing technique[J].Chinese J Comput Mech,2006,23:19-23.

[8]YANG H T,Xu M L.Solving inverse bimodular problems via artifcial neutral network[J]. Inverse Problems Sci Eng,2009,17:999-1017.

[9]YAO W J,YE Z M.Analytical solution of bending-compression column using diferent tensioncompression modulus[J].Applied Mathematics and Mechanics(English Edition),2004,25: 901-909.

[10]YAO M J,YE Z M.Analytical solution for bending beam subject to later for with diferent modulus[J].Applied Mathematics and Mechanics(English Edition),2004,25:1107-1117.

[11]YAO W J,YE Z M.The analytical and numerical solution of retaining wall based on elastic theory of diferent modulus[J].Journal of Shanghai Jiao Tong University,2004,38:1022-1027.

[12]何晓婷,陈山林,孙俊贻.不同模量简支梁均布荷载下的弹性力学解[J].工程力学,2007,24(10): 51-56.

[13]何晓婷,郑周练,陈山林.拉压不同模量弯压柱的近似弹性力学解[J].重庆大学学报,2008,31(3): 339-343.

[14]Qu C Z.Deformation of geocell with diferent tensile and compressive modulus[J].Elec J Geotech Eng,2009,14:1-14.

[15]高潮,刘相斌.用拉压不同模量理论分析弯曲板[J].计算力学学报,1998,15(4):448-455.

[16]吴晓,杨立军,孙晋.双模量圆板弯曲变形的计算分析[J].西安建筑科技大学学报,2009,41(1): 88-92.

[17]吴晓,杨立军,孙晋.双模量圆板弯曲变形的计算分析[J].西安建筑科技大学学报,2009,41(4): 485-488.

Biaxial bending of rectangular plates with diferent modulus

ZHANG Liangfei,YAO Wenjuan
(Department of Civil Engineering,Shanghai University,Shanghai 200444,China)

An eutral axis can be considered from two bending directions to solve the biaxial bending problem of rectangular plates with diferent modulus.Based on the diferent modulus theories,an equation of the neutral axis location is derived using the static equilibrium equation of rectangular plates with diferent modulus.The defection curve equation is solved with the Kantorovich method.Its solution agrees well with the fnite element solution.The result shows that the classical shell theory is not applicable in calculating defection of a rectangular plate when tensile and compressive modulus are quite diferent.The proposed method provides an approach to analyze the bending problem of other structure forms of plate with diferent modulus,and theoretical reference for engineering applications.

Kantorovich variational method;diferent modulus;biaxial bending

TU 36

A

1007-2861(2017)01-0128-10

10.3969/j.issn.1007-2861.2015.02.003

2015-01-03

姚文娟(1957—),女,教授,博士生导师,博士,研究方向为结构工程.E-mail:wenjuan@mail.shu.edu.cn