螺旋型埋管能源桩传热模型的适用性及其试验验证
赵海丰,桂树强,唐荣彬,杜金龙
(1.中国地质大学(武汉) 工程学院,武汉 430074;2.长江勘测规划设计研究院,武汉 430010;3.武汉科技大学 资源与环境工程学院,武汉 430080)
螺旋型埋管能源桩传热模型的适用性及其试验验证
赵海丰1,2,桂树强2,唐荣彬3,杜金龙2
(1.中国地质大学(武汉) 工程学院,武汉 430074;2.长江勘测规划设计研究院,武汉 430010;3.武汉科技大学 资源与环境工程学院,武汉 430080)
传热模型的精确性直接关系到能源桩换热效率的计算精度,进而影响能源桩设计。以螺旋型埋管能源桩为研究对象,在信阳地区开展了一项现场原位试验,实测获得了螺旋型埋管能源桩换热过程中的桩周温度场数据,并分别与圆柱面热源模型和线圈热源模型的计算成果进行了对比分析。研究成果显示:有限长热源模型较无限长热源模型具有更高的计算精度,有限长线圈热源模型较有限长圆柱面热源模型具有更高的计算精度,采用有限长线圈热源模型计算的桩壁温度误差<1.5%,桩周温度场计算误差<2.5%,地埋管进出口水温计算误差<2.2%,故将其推荐为螺旋型埋管能源桩桩周温度场的计算模型。最后,探索了不同传热模型针对螺旋型埋管能源桩的适用性,为指导螺旋型埋管能源桩设计提供了科学依据。
螺旋型埋管能源桩;圆柱面热源模型;线圈热源模型;桩周温度场;试验验证
1 研究背景
能源桩(energy piles)是将地源热泵系统的地埋管在桩基施工过程中埋置于桩基中,通过流体在桩基埋管中循环流动而达到与周边介质换热的效果,地埋管和桩基共同组成了地源热泵的地下换热系统,称之为能源桩,其属于土壤源地源热泵的一种新的应用形式[1]。目前国内外常见的能源桩埋管形式包括单U型、双U型、3U型、双W型和螺旋型等。螺旋型埋管能源桩是能源桩最常用的埋管型式之一,如图1所示。相比钻孔埋管换热器,能源桩取消了钻孔和回填材料的费用而具有更好的经济性;能源桩利用了混凝土结构较高的热储存能力和热传导性能,因而获得了比钻孔埋管换热器更高的换热效率;能源桩利用了桩基结构而节约了地下空间[2]。综上所述,能源桩具有良好的应用前景。

图1 螺旋型埋管能源桩示意图Fig.1 Schematic diagram of energy pile with spiral buried pipe
传统的钻孔埋管换热器与能源桩的主要差异在于换热器直径及长度的差异,能源桩深度一般为10~50 m,直径400~1 500 mm;而钻孔埋管换热器深度一般为80~120 m,直径80~150 mm。由于钻孔结构的长、细特点,在钻孔埋管传热计算时通常以钻孔壁为边界将传热分为钻孔外传热和钻孔内传热2部分。钻孔外的传热可简化为无限长或半无限长的线热源;而对于钻孔内的传热,由于钻孔孔径较小,一般假设其为稳态传热[3]。而对能源桩而言,由于其与钻孔埋管换热器在结构尺寸上的巨大差异,桩基孔壁与周围岩土体的传热不能简单地简化为线热源传热,而且,桩基内的传热要经过很长时间后才能达到稳态,因而也不能将桩基内的传热简化为稳态传热[4-5]。
目前适用于能源桩的传热模型主要有圆柱面热源模型和线圈热源模型,现有的文献主要针对传热模型及其对不同型式能源桩的适用性进行了一定的理论研究,但鲜有试验验证,因而无法检验传热模型的正确性。基于上述问题,本文以螺旋型埋管能源桩为研究对象,开展了一项现场原位试验,实测获得了能源桩的桩周温度场,然后分别采用圆柱面热源模型和线圈热源模型计算了其桩周温度场的解析解,通过解析解和实测成果对比分析验证了不同传热模型针对螺旋型埋管能源桩温度场计算的适用性。
2 试验方案
2.1 项目基本情况简介
本试验所依托的建筑主体为信阳高铁站站前广场,项目地点位于河南省信阳市城区北部,为地下2层建筑物,顶层为信阳高铁站站前广场,地下一层为商业建筑物,地下二层为停车场。该项目占地总面积约30 000 m2,建筑总面积为60 000 m2。本项目地源热泵冷热源系统的总冷负荷为7 200 kW,总热负荷为2 400 kW,选用2台高温地源热泵机组及2台冷水机。
地埋换热器系统采用桩基埋管与钻孔埋管相结合的复合埋管方式,其中地埋管井数量为360口,地埋管换热器采用de25的并联双U型管,竖直钻孔埋管方式,钻孔管径为130 mm,钻孔有效深度为100 m,埋管间距4.2 m×6 m。桩基埋管换热器数量为1 000口,桩基均采用人工挖孔桩,桩径800 mm,桩深12.0 m,桩基埋管采用螺旋型布管,管径25 mm。为了保证水力平衡,对钻孔埋管和桩基埋管分别设置集分水器。
2.2 试验布置
现场选择1根能源桩为测试对象,桩径为800 mm,长为12.0 m,测试桩采用螺旋型埋管,螺距为300 mm,地埋管管径25 mm,测试桩的总埋管量为80 m。
传感器布置详见图2所示。在测试桩的一侧桩壁和中心分别设置1列BGK-3700型温度传感器,定义为Z1和Z2;在测试桩的另外3侧桩壁设置BGK4200型振弦式应变传感器(可同时测试温度),分别定义为Tε1,Tε2和Tε3;在桩外侧的岩土体中布置4列温度传感器,间距425 mm,分别定义为Z3,Z4,Z5和Z6。每列温度传感器和应变传感器沿深度方向布置3组,分别位于桩顶以下1.5,6.0,10.5 m处。位于桩壁的传感器通过焊接的方式固定在钢筋笼上,随钢筋笼埋设在能源桩中;非桩体上的传感器采用钻孔埋设。

图2 测试桩监测仪器布置Fig.2 Layout of monitoring instruments in test pile
2.3 现场试验过程及测试结果
现场热响应测试仪采用中国地质大学(武汉)研制的GP-3岩土热响应测试仪,热响应测试(TRT)的测试时长为168 h。在试验过程中,热响应测试仪数据采集过程中每隔5 min自动采集进水口温度、出水口温度、流量、水泵功率、加热功率等参数,应变及温度采用人工读取数据,每隔20 min采集一次。测试过程中的进出口温度随时间的变化曲线如图3所示。

图3 测试桩进出口温度随时间的变化曲线Fig.3 Variations of temperatures at the inlet and outlet of test piles with time
3 传热模型及地埋管进出口温度计算
解析法是通过建立准确的传热模型,采用数学方法分析能源桩换热过程中的温度场。解析解实用性强,求解过程简单,而在实际工程中应用广泛,解析解的精确性主要取决于传热模型的精确性。
3.1 圆柱面热源模型
圆柱面热源模型是将换热器看成1个圆柱,将土壤看成无限大的传热介质,将柱热源放入初始温度均匀的无限大介质中而组成。圆柱面热源模型又分为空心圆柱面热源模型和实心圆柱面热源模型2种型式。空心圆柱面热源模型将能源桩假定为一空心截面,换热过程中将热量直接赋予到空心截面上而向土壤传递,由于该模型忽略了换热器孔内材料的影响,使得计算误差较大。实心圆柱面热源模型将孔内材料假定为均匀的介质,换热过程中将热量直接赋予实心介质,由于该模型考虑了能源桩内材料的热容量和尺寸,比空心圆柱面热源模型具有更高的精度。因此,本文仅介绍实心圆柱面热源模型。
(1) 无限长圆柱面热源模型。此模型将能源桩假定为一无限长的圆柱面热源,埋设在无限大均匀介质中,单位长度的发热量平均为qL(W/m),其温度响应的表达式为[6-7]
(1)

(2) 有限长圆柱面热源模型。由于能源桩长度有限,且其长径比远小于钻孔埋管换热器,因而有必要考虑能源桩长度对换热性能的影响,即采用有限长圆柱面热源模型。其温度响应的表达式为[8]
(2)
式中:h1为桩顶埋深(m);h2为桩底埋深(m);z为计算点的深度(m);erfc(x)为余补误差函数。
3.2 线圈热源模型
线圈热源模型是将能源桩简化为多个封闭线圈作为热源,线圈之间的间距为b,每个线圈的发热强度为qLb,且均匀发热。由于线圈热源模型与能源桩螺旋埋管换热器较为吻合,因而具有较好的适用性。
(1) 无限长线圈热源模型。无限长线圈热源模型将能源桩假定为一无限长的线圈热源,其温度响应的表达式为[9]
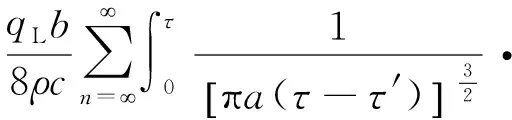
(3)
式中:b为螺距(m);n为线圈数;ρ为密度(kg/m3);c为比热容(J/( kg ·℃))。
(2) 有限长线圈热源模型。考虑到能源桩长度有限,为了更真实地模拟能源桩传热模型的实际状态,方肇洪等[6]、李新[10]提出了有限长线圈热源模型,其温度响应表达式为
(4)
3.3 地埋管进出口温度计算

管壁及管内热阻为
(5)
式中:d1,d2分别为管材的内径、外径;λP为管材的导热系数;h为循环液与管壁的对流换热系数。
埋管外壁面上的温度tb为
tb=θb+t0。
(6)
式中:θb为管壁过余温度;t0为初始地温。
螺旋埋管的长度Lp为
(7)
单位长度螺旋埋管承担的负荷qp为
qp=qL(h2-h1)/Lp。
(8)
管内循环液的平均温度为
(9)
计算进出口温度的表达式为
(10)
式中:t′为管内循环液的进口温度;t″为管内循环液的出口温度;M为循环液的质量流量。
单根能源桩承担的负荷为
Q1=qL(h2-h1)=cpM(t′-t″) 。
(11)
式中cp为循环液定压比热容。
(12)

表1 计算参数取值Table 1 Set values of calculation parameters
4 桩周温度场的解析解及其试验验证
以测试桩6 m深度位置的传感器测试结果为研究对象,分别通过圆柱面热源模型和线圈热源模型计算能源桩的桩周温度和地埋管进出口温度,并与实测值进行对比分析,以验证不同传热模型针对螺旋型埋管能源桩传热计算的适用性。
4.1 计算参数及取值
针对试验现场测试桩混凝土材料和岩土体进行了大量的热物性测试工作,包括现场实测和取样室内试验,同时,结合现场试验布置及测试成果,计算参数取值如表1所示。
4.2 壁面温度及其试验验证
4.2.1 无限长热源模型与有限长热源模型的比较
图4分别采用圆柱面热源模型和线圈热源模型对能源桩的壁面温度进行了计算,并与实测值进行了对比。从图4中可知,无论是圆柱面热源模型还是线圈热源模型,其计算值均低于实测值,且有限长热源模型的计算值更为接近实测值,即有限长热源模型相比无限长热源模型具有更高的计算精度。有限长和无限长热源模型的计算值在初始阶段差距较小,而后随着时间的增加,差距逐渐增加,但有限长热源模型的计算值始终更接近于实测值。

图4 壁面温度解析解与实测值对比Fig.4 Comparison between analytical solution and measured values of tube wall temperature
4.2.2 有限长圆柱面热源模型与有限长线圈热源模型的比较
有限长圆柱面热源模型与有限长线圈热源模型壁面温度计算值与实测值及其相对误差对比见图5。
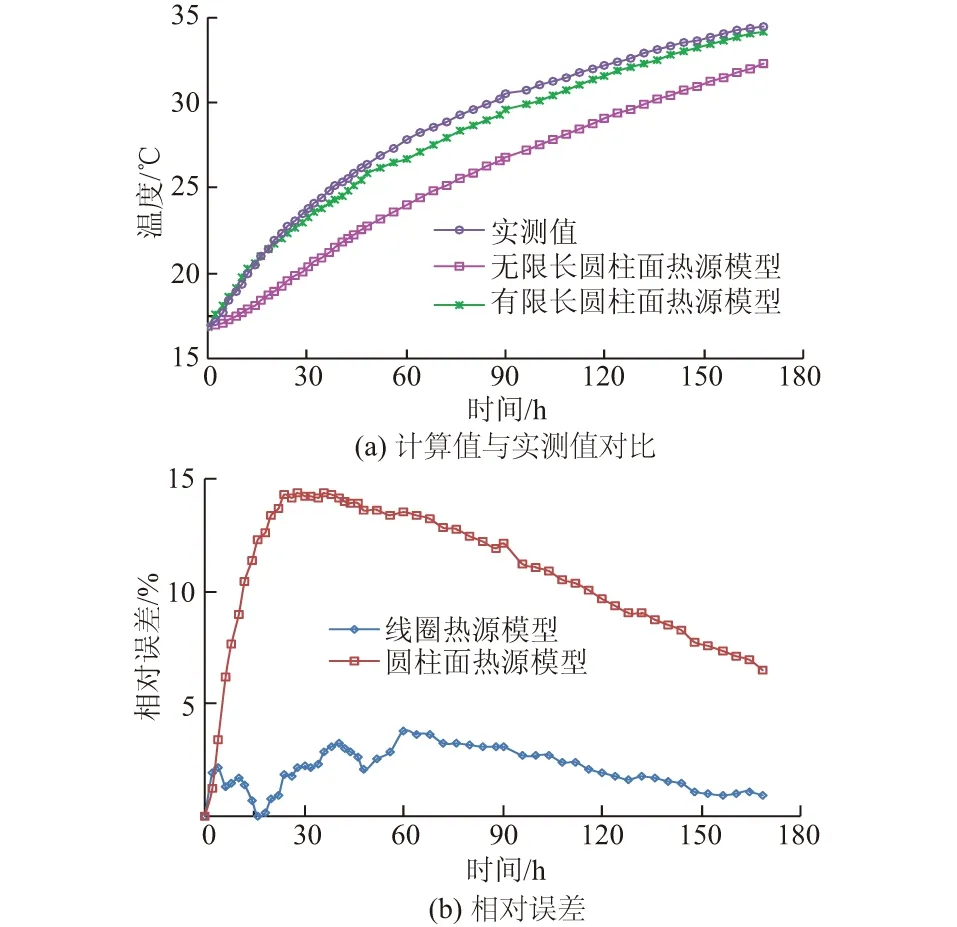
图5 有限长热源模型计算值与实测值及其相对误差对比Fig.5 Comparison between calculated and measured values of tube wall temperature and relative errors in heat source model with finite length
从2个传热模型的计算误差来看,线圈热源模型的相对误差远小于圆柱面热源模型,即线圈热源模型较圆柱面热源模型具有更高的精度。圆柱面热源模型的计算相对误差在初始阶段上升很快,约30 h后达到峰值,误差约15%,而后随着时间的增加,计算误差逐渐下降,最终误差为6.5%,分析主要原因在于圆柱面热源模型将温度一次性施加给整个能源桩,忽视了桩内传热而造成了较大的计算误差,随着时间的增加,桩内温度逐渐升高,传热过程趋于稳定而计算误差逐渐下降。有限长线圈热源模型的相对误差在初始阶段波动值较大,但总体随时间的增加而增大,达到峰值后,而后随着时间的增长缓慢下降,试验结束时的相对误差约为1.5%。
由此可见,线圈热源模型考虑了能源桩螺旋埋管的管径、节距、桩径等因素,其计算结果能较精确地反映能源桩的传热过程。
4.3 桩周温度场及其试验验证
图6为TRT试验结束时,分别采用有限长圆柱面热源模型和有限长线圈热源模型计算获得的桩周温度场与实测值的对比图。

图6 桩周温度场计算值与实测值对比Fig.6 Comparison between calculated and measured values of temperature field around the energy pile
由图6可知,2种传热模型的计算温度值均低于实测值,且有限长线圈热源模型计算的桩周温度更为接近实测值。从计算误差来看,在距离桩壁0.8 m范围内,有限长圆柱面热源模型的平均计算误差约为10%,有限长线圈热源模型的平均计算误差约为2.5%。由此可见,有限长线圈热源模型具有更高的计算精度,更适宜作为螺旋型埋管能源桩周温度场的计算模型。
4.4 地埋管进、出口温度及其试验验证
图7为采用有限长线圈热源模型计算的进出口温度与实测值的对比图。由图7可知,计算值与实测值表现为较好的一致性,两者的进水温度平均计算误差为2.2%,出水温度平均计算误差为6.0%,再次验证了线圈热源模型针对螺旋埋管能源桩的适用性。
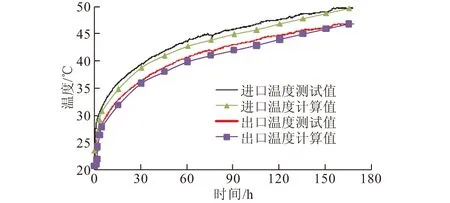
图7 进出口温度计算值与测试值对比Fig.7 Comparison between calculated and measured values of temperature at the inlet and outlet
5 结 论
本文以螺旋型埋管能源桩为研究对象,分别采用圆柱面热源模型和线圈热源模型计算了螺旋型埋管能源桩的桩周温度场和地埋管进出口温度,并进行了试验验证,得到了以下主要结论:
(1) 分别采用有限长热源模型和无限长热源模型对能源桩周边温度场进行了计算并与实测值进行了对比,有限长传热模型较无限长传热模型具有更高的精度,更适用于能源桩的传热计算。
(2) 通过对2种有限长传热模型对能源桩壁面温度的计算成果对比分析,能源桩传热模型的计算精度随着时间的增加逐渐提高,且有限长线圈热源模型的计算精度明显高于有限长圆柱面热源模型,其最终的计算误差<1.5%,适宜作为计算螺旋型埋管能源桩壁面温度的理想模型。
(3) 有限长线圈热源模型对桩周温度场具有更高的计算精度,平均计算误差<2.5%,建议作为螺旋型埋管能源桩桩周温度场的计算模型。
(4) 采用有限长线圈热源模型计算获得的进出口水温与实测值具有一致性,两者的进水温度平均计算误差为2.2%,出水温度平均计算误差为6.0%,可作为计算螺旋型埋管能源桩进出口水温的计算模型。
[1] BRANDL H. Thermo-active Ground-Source Structures for Heating and Cooling[J]. Procedia Engineering, 2013,57(1): 9-18.
[2] 桂树强,程晓辉,张志鹏. 地源热泵桩基与钻孔埋管换热器换热性能比较[J]. 土木建筑与环境工程, 2013,35(3): 151-156.
[3] 方肇洪, 刁乃仁, 曾和义. 地热换热器的传热分析[J]. 工程热物理学报, 2004,25(4): 685-687.
[4] 余乐渊,赵 军,李新国,等.竖埋螺旋管地热换热器理论模型及实验研究[J].太阳能学报,2004,25(5):690-694.
[5] 张文克.桩埋管地热换热器的传热模型研究[D].济南:山东建筑大学,2009.
[6] 刘俊红,张克文,方肇洪.桩埋螺旋管式地热换热器的传热模型[J].山东建筑大学学报,2010,25(2):95-100.
[7] 张克文,刘俊红,黄体士,等.桩埋管地热换热器的传热分析[J].制冷与空调,2009,23(4):105-108.
[8] MAN Y, YANG H X, DIAO N R,etal. A New Model and Analytical Solutions for Borehole and Pile Ground Heat Exchangers[J]. International Journal of Heat and Mass Transfer, 2010, 53(13/14): 2539-2601.
[9] 李 新,方 亮,赵 强,等. 螺旋埋管地热换热器的线圈热源模型及其解析解[J]. 热能动力工程, 2011,26(4): 475-479.
[10]李 新.能量桩的传热研究与工程应用[D]. 济南:山东建筑大学, 2011.
(编辑:占学军)
Applicability of Heat Transfer Model of Energy Pile with BuriedSpiral Pipe and Its Experimental Verification
ZHAO Hai-feng1,2,GUI Shu-qiang2,TANG Rong-bin3,DU Jin-long2
(1.Faculty of Engineering, China University of Geosciences, Wuhan 430074, China; 2.Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430010, China; 3. School of Resource and Environmental Engineering, Wuhan University of Science and Technology, Wuhan 430080,China)
Accuracy of heat transfer model is directly related to the computational accuracy of heat transfer efficiency of energy pile, which influences the design of energy piles. Taken energy pile with buried spiral pipe as the research object, an in-situ test was conducted in Xinyang area, Henan province. Then, measured data such as temperature field around the pile was acquired, and calculation results of the cylindrical heat source model and the coil heat source model are respectively compared with measured data. Research results show that the computational accuracy of heat source model with finite length is higher than that of heat source model with infinite length. Coil heat source model with finite length is more accurate than cylindrical surface heat source model with finite length. The calculation error of tube wall temperature in coil heat source model with finite length is less than 1.5%, the calculation error of temperature field around the pile is less than 2.5%, and the water temperature at inlet and outlet of buried pipe less than 2.2%, respectively. In view of this, coil heat source model with finite length is recommended for calculating temperature field in energy pile with spiral buried tube. The applicability of different heat transfer models for the spiral pipe pile was explored, and can be taken as reference for the design of energy pile with buried spiral tube.
energy pile with buried spiral pipe; cylindrical heat source model; coil heat source model; temperature field around pile; temperature field around the energy pile; experimental verification
2016-01-29;
2016-04-08
国家自然科学基金项目(41502238);中央高校杰出人才培育基金项目(CUGL150819)
赵海丰(1983-),男,湖北武汉人,高级工程师,博士,主要从事浅层地热能开发利用及岩土工程设计、科研工作,(电话) 027-87531540 (电子信箱) zhaohaifeng83@163.com。
唐荣彬(1992-),女,土家族,湖北恩施人,硕士研究生,主要从事土地资源管理及浅层地热能开发利用工作, (电话) 15527286351 (电子信箱) 237664585@qq.com。
10.11988/ckyyb.20160098
2017,34(4):111-116
TU473.1
A
1001-5485(2017)04-0111-06

