数学中的变形技巧研究
蔡晓赛
(广东技术师范学院天河学院,广东广州 510540)
数学知识点比较抽象,知识结构非常松散,如果在脑海中没有形成缜密的数学思维,很有可能会在学习中遇到很多难点问题,再加上数学题目本身的复杂性特点,这些都对于学生的思维能力和计算能力提出了很高的要求。因此学生们在掌握数学基础知识的基础上,还需要同时具备解题技巧,把复杂的数学问题进行简单化处理,应用变形技巧找到问题解答方式,因此变形技巧是数学学习过程中必须要掌握的答题技巧之一。
1 数学变形技巧
目前在数学教材当中,并没有具体的把数学变形内容界定出来,一般在解答题目过程中,经常使用的数学变形技巧有三种方式,逻辑方式、一般方式和特殊方式,在逻辑方式当中又分成了反证法和分析法,而一般方式则是按照数学题目计算的基本原则进行问题解答,特殊方式则是需要在计算过程中应用换元法、公式法等进行问题解答[1]。在数学题目解答过程中,如果题目给出的已知条件并不是很明显,就需要深入的挖掘题目给出的算式之间的关系,在题目解答过程中如果熟练掌握了变形技巧,就能够挖掘出题目中暗藏的隐形条件,有效提升数学问题答题效率。在数学题目解答过程中应用变形技巧,可以把分散的题目元素集中起来,转化问题的形式,能够找到相应的公式和定理,从而找到问题解答的正确思路。只要能够在数学题目解答过程中掌握一定的变形技巧,就能够有效降低题目的复杂程度,帮助提升问题解答效率。
2 数学问题解答中的变形技巧分析
2.1 三角函数等量变换技巧
在计算三角函数类似题目时,需要针对三角函数进行等量变换,把复杂性的三角函数变换成为简单的形式,在数学题目中涉及到使用三角函数进行等量变换的题目有很多种,比如说解三角方程、题目中需要证明出三角几何的关系、针对三角方程进行变形化简等,通常在三角等量代换当中,三角函数等量代换的应用十分广泛。三角函数在变换过程中可以使用的公式也有很多种,主要看题目的需要来选择三角函数等量变换的应用技巧[2]。在题目计算过程中,我们如果熟练地应用各种公式的应用技巧,就能够不管面对什么问题,都能够合理的选择正确的三角恒等变换形式,帮助加深学生们对于公式的学习印象,全面的了解不同的三角公式之间存在的联系性。通过在三角函数中应用变形技巧,还能够发散学生数学学习思维。在学生面对三角函数问题进行等量变换时可以使用三种方法,合理的转换三角函数,找到三角函数当中存在的内在联系,并寻找在三角函数中存在的不同之处。学生如果能够准确的掌握了三角公式的二倍角、差、和的运算方法,就能够准确解答三角问题。学生们首先要学会在题目中创造条件,才能够提升自身转变三角能力,在题目计算过程中熟练地应用各种三角公式,把复杂的问题简单化处理。
2.2 因式分解的变形技巧
必须要掌握完善的代数变形技巧,才能够解决实际的数学问题,而学生们对于变形技巧的掌握能力[3],在一定程度上也代表了学生们的数学问题解答能力。变形技巧的目标就是为了能够简化数学问题的计算流程,能够方便学生进行思考和计算,变形技巧是一种数学问题解答技能,需要同学们经过反复的计算和练习,才能够体会到技巧的真谛。在数学学习过程中代数的学习非常重要,在历届高考数学试卷中也会经常有针对代数知识的考题,因此学生们需要掌握一定的变形技巧,针对代数学习中遇到的指数和对数进行变形,明确出解题思路,在解题中给自己创造条件,之后就可以使用拆分、化简和加减变形的方式来针对公式进行因式分解。在因式分解过程中经常会使用两种方法,分组分解法和提公因式法。例如说有一道课后练习题是因式分解题目,其中有一个多项公式:4x2-12xy+9y2,很多学生第一次看见这道题目,基本上都会选择使用公式法进行因式分解,但是在短时间内却找不到任何能够变形的项目,此时教师可以引导学生使用系数变换,针对因式进行变形转换,从而能够得出 (2x)2-2(2x)(3y)+(3y)2=(2x-3y)2,这样能够准确的把因式从复杂转变成简单。
2.3 一元二次方程变形技巧
在学习一元二次不等式、二次函数时,可以应用变形技巧熟练解答一元二次方程。在解答一元二次方程相关类型题目时,经常会需要使用到变形技巧,学生需要在解答这一类题目过程中反复的阅读已经知道的题目条件,认真的分析一元二次方程的结构特点,寻找出题目中给出的条件和方程式存在的内在联系,最后结合已知条件正确的解答一元二次方程[4]。在实际计算过程中,可以从题目的结论出发进行思考,把已知条件带入到题目当中,结合方程具体特点选择合适的方式进行变形。例如说:已知一元二次方程 x2-x-1=0,a和 b是方程的解,求a4+3b的值。在详细分析这道题目之后我们可以看出,如果先分别把 a和 b的值求取出来,在进行 a4+3b的计算,这个过程非常复杂,会消耗大量的计算时间,并且也无法确保在计算过程中不会出现任何错误,因此就可以使用相应的变形技巧,提升解题效率。由于a是方程x2-x-1=0的解,可以变成a2-a-1=0,得出a2=a+1,因此方程式可以变形成为a4(a+1)2=a2+2a+1=a+1+2a+1=3a+2,a4+3b=3a+2+3b=3(a+b)+2,由于题目中给出了a和b是方程的解,所以a2+b=1,a4+3b=5.
2.4 数列变形应用
数列知识在数学中同样属于非常重要的知识点,数列的主要研究方向就是求和问题,因此针对复杂的数列题目类型,可以采取变形通项的方式进行思考和解答,把复杂的数列能够转换成为熟悉的数列求和问题。在数列变形过程中经常使用的方法时错位相加法、倒序相加法以及分组转化法等。例如说在题目:求数列an=(2n+2= 1/3n)的前n项和Sn。分析该数列的前半部分为等差数列,后半部分为等比数列。通项公式表达为an=bn+cn,bn=(2n=2),cn= .分组求bn、cn。前n项和S1、S2。那么则能够得出结论:
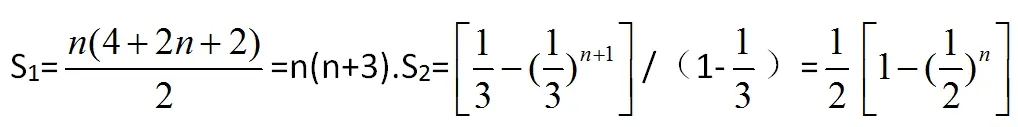
在数列问题解答过程汇总,如果发现了数列同时拥有等差数列和等比数列的特点,可以适当分解类数列,拆解成为等差或者是等比的常见数列,然后再把数列进行求和计算,能够有效化整为零,利用分组相加解答数列问题。
结语
综上所述,在数学教学中引导学生掌握数学变形技巧,能够有效把数学问题从繁化简,通过变形直观的看出数值的变化过程,能够更加方便数学题目的解答。数学变形技巧非常的抽象和集约,因此学生需要在变形过程中深入理解,才能够准确灵活的应用在数学题目解答过程中,提升自身的数学技能,达到提升做题准确率的效果。
[1]冯麟清.探讨数学中的变形技巧[J].智库时代,2017(10):114+118.
[2]邹美婷,孔翠碧.浅谈数学中的变形技巧[J/OL].当代教育实践与教学研究:1-3[2018-01-11].
[3]程鲁,蒋鹏飞.浅谈数学中的变形技巧[J].数学学习与研究,2016(13):123.
[4]陈东磊.浅谈数学中的变形技巧[J].科教文汇(上旬刊),2012(05):108-109.

