上海市PM2.5浓度统计释用综合集成研究

李亚云,束 炯*,沈 愈

(1.华东师范大学,教育部地理信息科学重点实验室,上海 200241；2.上海市气候中心,上海 200030)

上海市PM2.5浓度统计释用综合集成研究

李亚云1,束 炯1*,沈 愈2

(1.华东师范大学,教育部地理信息科学重点实验室,上海 200241；2.上海市气候中心,上海 200030)

在WRF模式输出的基础上,结合卡尔曼滤波(KALMAN)、偏最小二乘回归(PLS)和辨识理论实时迭代统计方法(RTIM)组成3种模式输出统计预报(MOS),并运用这3种MOS模式分别建立多模式平均、递归正权综合和多元线性回归集成模式,对上海市2014年12月2日～31日(PM2.5轻度污染天气过程)以及2015年12月15日～2016年1月13日(PM2.5重污染天气过程)进行了1d、2d和3d的PM2.5日均浓度试预报.结果表明:相比于3种单一的MOS模式,集成模式通过获取更为准确的信息而减少了系统误差,这不仅可以提升对污染天气过程的预报能力,且有可能降低污染过程中决策失败的风险.通过对PM2.5轻度污染天气和重污染天气过程预报的比较分析,多元线性回归集成模式整体预报显示出更高的精度和稳定性.统计释用方法综合集成模式对于PM2.5预报显示出良好的性能,可为业务化预报模型的选择提供可借鉴的参考.

PM2.5；多元线性回归；综合集成；递归正权综合；WR F

近年来,随着经济的快速增长和城市化进程的不断加速,由PM2.5引发的高污染天气在长江三角洲等东部发达区域日益严重[1-3].据《2014中国环境状况公报》显示,长江三角洲区域全年以PM2.5为首要污染物的污染天数最多,其中PM2.5年均浓度超标城市占96%,而PM2.5对人体健康危害极大[4-5].上海作为一个经济发达、人口密集的大城市,冬季频繁发生以PM2.5为首要污染物的低能见度霾天气,这一现象近年来愈演愈烈[6].为了向公众及时、准确、全面地提供空气污染变化的信息,作好PM2.5预报,及时进行防控,对于市民的健康具有重要的意义.

目前,国内外关于空气质量预报的方法主要有数值预报[7-9]、统计预报和模式输出统计预报.数值预报方法在大气动力学模式的基础上耦合了化学模块,是目前最先进的预报模型,但是由于地面排放清单本身的不确定性以及与化学反应方程的匹配等因素,该方法在业务化应用和精度上存在一定的局限性.统计预报方法根据地面、高空气象资料和污染物浓度资料,筛选出与污染物相关较强的气象因子建立定量关系,一般多用多元分析[10-13]、神经网络[13-17]和卡尔曼滤波[18-20]等,在早期污染预报发挥较大的作用.模式输出统计预报(MOS)[21-25]方法结合了数值模式对天气形势预报的准确性以及统计模式对局地污染天气定量化预报的优点,既可以避免物理-化学耦合数值模式对某些局地污染条件的错误估计,又可以与之形成优势互补.由于不同MOS方法对于PM2.5的预报结果不同,存在各自的优缺点.因此如何有效利用不同的MOS方法提高污染预报精度成为目前急需解决的问题.

Krishnamurti等[26-27]1999年将集成(对多个预报模型的预报结果进行合理集成)思想运用到多个数值预报模式中,提出了超级集合预报方法.随后的诸多研究表明[28-33],对于订正气象数据(温度,降水等),超级集合预报模式可减少模式系统性误差,提供的信息比单个集合模式更准确.近年来,集合思想逐渐引入到空气质量预报中,王自发等[34]、唐晓等[35]、黄思等[36]、陈焕盛等[37]分别采用权重集成方法、蒙特卡罗集合预报方法、多元线性回归集成方法集成各空气质量模式,预报北京市PM10和O3浓度以及广州市PM10浓度,结果均表明集成预报模式优于单个预报模式.这些模式多是对基于大气动力学-化学耦合模式的集合预报[34-40],而对于动力[41]-统计的释用预报研究仍不多见.因此本文利用算术平均、多元线性回归[37]和递归正权方法集成WRFKALMAN[6]、WRF-PLS[2]和WRF-RTIM[42-43]3种MOS方法,对上海冬季PM2.5日均浓度进行试预报,并对3种集成模式的预报结果进行非参数检验和参数评估.

1 资料与方法

1.1 资料

上海PM2.5日均浓度(上海市8个国控污染监测点PM2.5数据的平均值)由上海市环境监测中心提供,选自每年污染高发的时节,时间段为2013年1月2日～2016年1月13日的冬季.用于建模的相应历史气象资料来自美国国家海洋和大气局网站(https://gis.ncdc.noaa.gov/maps/clim/cdo/hourly),考虑到地域上更能覆盖国控污染监测点的空间范围,分别选用了靠近市中心和沿海的虹桥和浦东机场观测记录.

本预报是基于WRF模式预报输出要素,作为下一步统计预报模式的备选因子.选取预报因子的标准主要是考虑与污染密切相关的气象要素,其中日均风速反映大气平流输送能力的强弱;日均气压反映所处地气压场的高低;24h变压反映所处地大气中热力和动力因素对气压的影响,以判断天气系统的移动与强度变化趋势,间接反映大气的稳定状况;24h变温反映所处地气压场等天气变化趋势;日最低气温是在稳定天气条件下预示逆温出现与否的重要标志;风向反映了天气系统的移动趋势和污染物质的输送规律;日均相对湿度反映了气溶胶粒子吸湿性凝结增长的条件,并与大气稳定度有关;前一天日均气温和风速可反映天气系统的连续变化过程.由此,相应的历史资料选取包括了日均风速、日均温度、日均风向,日均气压、日均相对湿度、前一天的PM2.5日均浓度、日均气温、前一天日均风速、日最高气温、日最低气温、24h变压和24h变温等因子.

这种动力-统计模式并不涉及气溶胶粒子形成的化学转化机制和微物理性质,但是适当因子的选择却能反映气溶胶物理化学过程变化的统计规律和动力过程提供的外部条件.前一天PM2.5日均浓度与上述模式预报的气象要素综合考量,可以在统计意义上推算未来气溶胶浓度的变化趋势.

用逐步回归方程从历史数据中筛选出预报因子.其基本思路为,在上述2个站气象因子X1～Xn(n=1～23)中,按每个因子Xn对Y(PM2.5)的作用大小(按0.05的显著性检验),从大到小逐个引入回归方程,每一步进行F检验反复筛选,直至回归方程建立.

风向不是个数量化因子,故不能直接参与计算,对风向进行量化处理的方法是:利用每小时浓度的历史资料,求出近地面层16个方位风向对应的PM2.5日均浓度值[44-45].

1.2 综合集成预报方法

1.2.1 WRF模式输出 本文采用了3.6.1版的WRF模式,模拟区域采用Lambert投影,WSM3云物理参数化方案,YSU边界层参数化方案, Kain-Fritsch积云对流参数化方案,Dudhia短波辐射参数化方案,RRTM长波辐射参数化方案以及Noah陆面过程方案.设置四重嵌套,水平格距分别为81,27,9,3km.气象初始场和边界条件使用GFS全球预报场数据,边界条件每6h更新一次.从模式计算输出的诸多因子中,选取与逐步回归方程筛选出的相同因子,作为新的预报自变量,参与统计模式预报.

1.2.2 统计预报模型 (1)卡尔曼滤波(Kalman filtering)

采用状态方程和量测方程组成的线性随机系统的状态空间模型来描述滤波器,并利用状态方程的递推性,按线性无偏最小均方差估计准则,采用递推算法对滤波器的状态变量作最佳估计,从而求得滤掉噪声的有用信号的最佳估计.利用最小二乘法可以得到卡尔曼滤波的递推方程组,据此进行预报[46].

(2)偏最小二乘回归(PLS)

集中了主成分分析、典型相关分析和线性回归分析方法的特点,可以有效解决样本个数少于变量个数等问题.假设有1个因变量y与p个自变量x1,x2,…,xp,观测样本点为n,记为X=(xij)n×p= (x1,x2,…,xp)和Y=(yij)n×1=(y),分别在X和Y中提取第一主成分t1和u1,并且要求t1和u1应尽可能大地携带各自的变量系统中的变异信息,且相关程度达到最大.在第一主成分t1和u1被提取后,偏最小二乘回归方法分别实施X对t1的回归以及Y对u1的回归,如果回归方程已经达到满意的精度,则算法终止;否则进行第二轮成分提取,直到达到一个满意的精度[47].

(3)基于辨识理论的实时迭代统计(RTIM)

系统辨识是根据系统的输入输出来确定描述系统行为的数学模型.由于预报系统是随时间变化的随机系统,为了强调最近样本对预报值的贡献而加入实时迭代功能.在参数估计时,按时间序列赋予输入样本不同的权重,以凸显当前预报值状况的重要性.根据初始样本用最小二乘法确定预报模型,预报次日污染物浓度时,输入值为WRF模式输出的次日气象场预报值和当日污染场数据[42-43].

1.2.3 多元线性回归集成 本文采用多元线性回归方法建立多元线性回归集成模式,将3种MOS模式下对上海PM2.5日均浓度的预测时间序列分为2部分,分别为训练和检验2个阶段.在训练阶段,利用3种MOS模式的预报值与实测值确定3种MOS模式的回归系数,用于检验阶段多元线性回归集成模式的建立.

(2)在训练阶段,对于上海PM2.5日均浓度:

式中:S是训练期的实测值,μg/m3;是训练期的实测值平均,μg/m3; ai是参与集成的第i个MOS模式的权重系数;Fi和分别是第i个MOS模式的预报值和其在训练期的预报平均值.其中权重系数ai有训练期的误差E的最小化获得:

式中:yt和st分别是训练期的实测值和集成模式的预报值,μg/m3.

(3)确定多元线性回归模型的权重系数

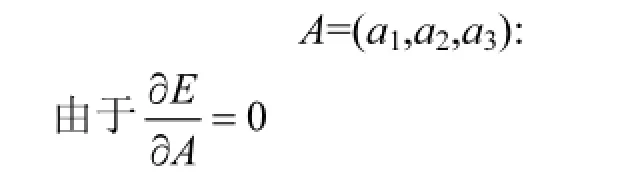
(4)多元线性回归集成模式的建立

1.2.4 平均集成 对3种MOS模式集成成员进行算术平均作为最终的集成预报结果.方程为:

式中:Fi为第i个模式的预报值,μg/m3;n为参与集成的MOS模式总数.

1.2.5 递归正权综合集成 本文采用均方倒数加权法建立递归正权综合集成模式,将3种MOS模式对上海PM2.5日均浓度的预测时间序列分为2部分,分别为训练和检验2个阶段.在训练阶段,计算各种MOS模式的预报值与实测值之间的误差平方和,采用递归正权优化确定各个MOS模式的权重系数,用于预报阶段递归正权综合集成模式的建立.

(1)各集成成员的误差平方和ej:

式中:Ot训练期实测值,μg/m3;Ft(j)训练期各集成成员的预报值,μg/m3;j为集成成员的数量;n为训练期的时间样本数.

(3)定权重系数W:

(4)计算训练期递归正权综合集成模式的预报值:

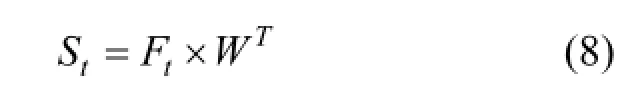
式中:Ft=(Ft1,Ft2,Ft3);t表示训练期的时间样本数;Ft表示训练期各集成成员的预报值.

计算递归正权综合集成模式的误差平方和e:

式中:Ot训练期实测值,μg/m3;St训练期递归正权综合集成模式的预报值,μg/m3.

(5)用e取代max.

(6)重复步骤(2)～步骤(4)直到max-min达到最小为止,得到新的e1,e2,e3,从而得到新的权重系数W.

(7)递归正权综合集成模式的建立:

式中:Ft=(Ft1,Ft2,Ft3),t表示预报期的时间样本数; Ft表示预报各集合成员的预报值.

集成成员包括WRF-KALMAN模式、WRF-PLS模式和WRF-RTIM模式.本文构建2套样本检验模型的预报效果.

轻污染天气过程:PM2.5轻度污染天气过程是指集成模式预报时段(2014年12月2日～31日)发生PM2.5污染过程时,浓度集中在76～150μg/m3之间.研究中所用PM2.5和气象观测资料为2013年1月1日～2014年12月31日的冬季,其中2014年2月15日～12月31日资料没有参与分析和建模,而是用于模型(WRF- KALMAN、WRF-PLS和WRF-RTIM模式)的检验,进行1d、2d和3d试预报.

2015年12月15日～2016年1月13日上海发生了连续的PM2.5重污染天气,为了检验集成模型对PM2.5重污染天气的预报效果,构建重天气污染过程样本:PM2.5重度及以上污染天气过程是指集成模式预报时段(2015年12月15日～2016年1月13日)发生PM2.5污染过程时,峰值浓度多集中高于150μg/m3.研究中所用PM2.5和气象观测资料为2013年2月18日～2015年1月15日和2015年12月12日～2016年1月13日的冬季,其中2015年1月14～15日以及2015年12月12日～2016年1月13日资料没有参与分析和建模,而是用于模型(WRF-KALMAN、WRF-PLS和WRF-RTIM模式)的检验,进行1d、2d和3d试预报.

上述2个样本集的试预报样本前15d(轻污染天气过程:2014年2月14日～2014年12月1日;重污染天气过程:2015年1月4～15日以及2015年12月12日～14日)作为多元线性回归、算术平均以及递归正权综合集成模式的训练期,利用各MOS模式预报值与实测值确定权重系数,后30d(轻污染天气过程:2014年12月2日～31日;重污染天气过程:2015年12月15日～2016年1月13日)则作为上述3种集成模式的预报期,检验预报效果.

本文构建2套样本集的目的是检验集成模式的稳定性,提高集成模式的普适性.

1.2.6 模型预报评价参数 本文选用相关系数(COR)、均方根误差(RMSE)和临界成功指数(CSI) 3种评价参数,分析其预报效果:

式中:Sim表示预报值;Obs表示实测值;Nmodelk代表预报为正类(以《环境空气质量标准》中二级浓度标准[48]作为分类标准,PM2.5日均浓度(单位:μg/m3)超过75μg/m3为正类,否则为负类)且实测确为正类的样本数; Nmodelf代表预报为正类的样本数;NObs代表实际为正类的样本数;N 代表预报总样本数.均方根误差(RMSE)显示预报值和观测值的偏离情况;相关系数(COR)是反映预报值和观测值的相关程度,即预报值和观测值之间变化趋势的吻合程度.临界成功指数(CSI)是预报正确的样本数与预报正确和漏报数之和的比值,去检验集成模式的预报性能.

2 结果分析

2.1 非参数检验

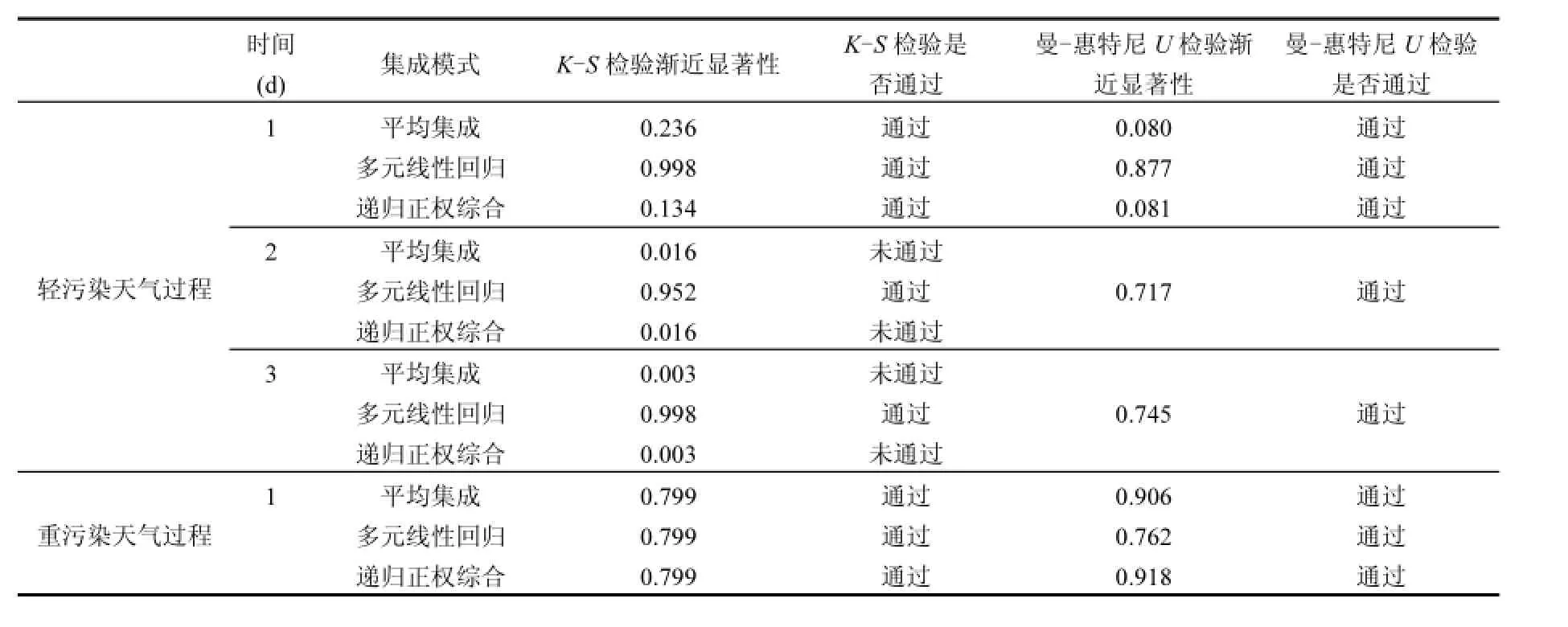
表1 3种集成模式1d、2d和3d的K-S和曼-惠特尼U检验结果分析Table 1 Analysis of K-S and Mann Whitney U test results about three kinds of integration models on one day、two days and three days

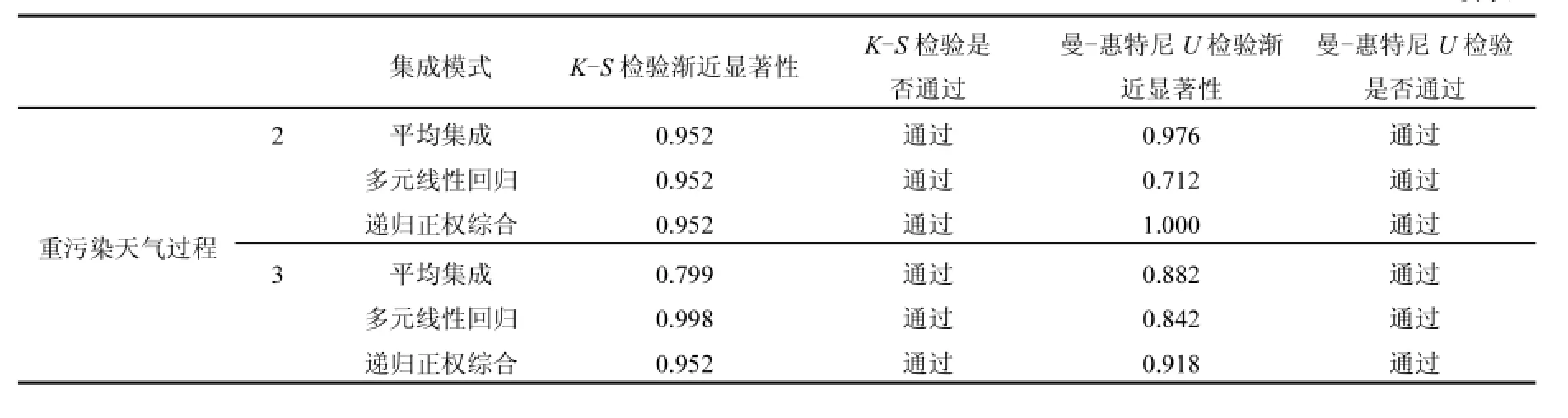
续表1

本文对3种集成模式的预报值与相对应的实测值进行非参数检验,先用K-S检验对3种集成模式的预报值与相对应的实测值的总体分布是否存在显著性差异进行检验,然后再利用曼-惠特尼U检验对3种集成模式的预报值和实测值的均值进行检验.检验结果表1.

在进行2个独立样本K-S检验和曼-惠特尼U检验时,分别假设2个样本的总体分布和均值无显著性差异,且显著性水平为0.05,如果渐近显著性(伴随概率)大于0.05,说明2个样本的总体分布和均值无显著性差异,否则相反.从表1可以看出,3种集成模式的预报值和实测值进行K-S检验时,多元线性回归集成模式任意样本和时长都通过检验, 而多模式平均集成模式对于轻污染天气1d和2d的预报没有通过检验，递归正权综合集成模式对于轻污染天气2d和3d的预报没有通过检验.对3种集成模式通过K-S检验的样本和时效进行曼-惠特尼U检验,都通过检验.说明多元线性回归集成模式任意样本和时长预报值的总体分布和实测值的总体分布是无差异的,且均值也是无差异的;而多模式平均集成模式和递归正权综合集成模式对轻污染天气2d和3d的预报值与实测值总体分布和均值存在差异.表明多元线性回归集成模式的稳定性优于多模式平均集成模式和递归正权综合集成模式.

2.2 结果与参数评价分析

2.2.1 预报结果分析 由图1的预报结果比对和表2的偏差分析可见,无论对于轻污染还是重污染天气,任何时长的预报,平均权重和递归正权综合集成模式的预报值相对实测值多数时段偏高,多元线性回归集成模式的预报值和实测值一致性较好;从轻污染天气预报时段的峰值来说,平均权重和递归正权综合集成模式对12月24日和29日的峰值预报好于多元线性回归集成模式.对于重污染天气任何时长的预报,3种集成模式的预报值相对实测值多数时段偏低;对于重污染天气的峰值预报来说,3种集成模式的预报值普遍偏低;但对于预报时段的低值来说,3种集成模式的预报值和实测值一致性相对来说较好一些.除此之外,平均权重和递归正权综合集成模式的预报值十分一致,主要是因为平均权重是正权综合决策模型的一种,相近的预报结果是可以理解的.结合表2,对于轻污染天气预报,多元线性回归集成模式的最大正偏差高于平均和递归正权综合集成模式,最大负偏差低于平均和递归正权综合集成模式.对于重污染天气预报,3种集成模式的最大正负偏差均大于轻污染天气,预报值普遍存在峰值预报偏低的现象;多元线性回归集成模式的最大正偏差低于平均和递归正权综合集成模式,最大负偏差基本上高于平均和递归正权综合集成模式.

为更直观地分析预报结果,绘制了对数坐标相关分析图.由图2可见,3种集成模式对于任何样本任何时长的预报值主要集中在实测值附近,预报值和实测值较好的一致性说明3种集成模式均能较好地预报上海市PM2.5日均浓度.对于任何时长轻污染和重污染天气的预报,多元线性回归集成模式的预报效果优于平均权重和递归正权综合集成模式3种集成模式对于轻污染天气任何时长的预报结果整体偏高于实测值,且平均权重和递归正权综合集成模式的偏高程度较大;重污染天气下,3种集成模式的预报结果出现低值偏高、高值偏低的现象;3种集成模式预报值和实测值离散度大于轻污染天气的.

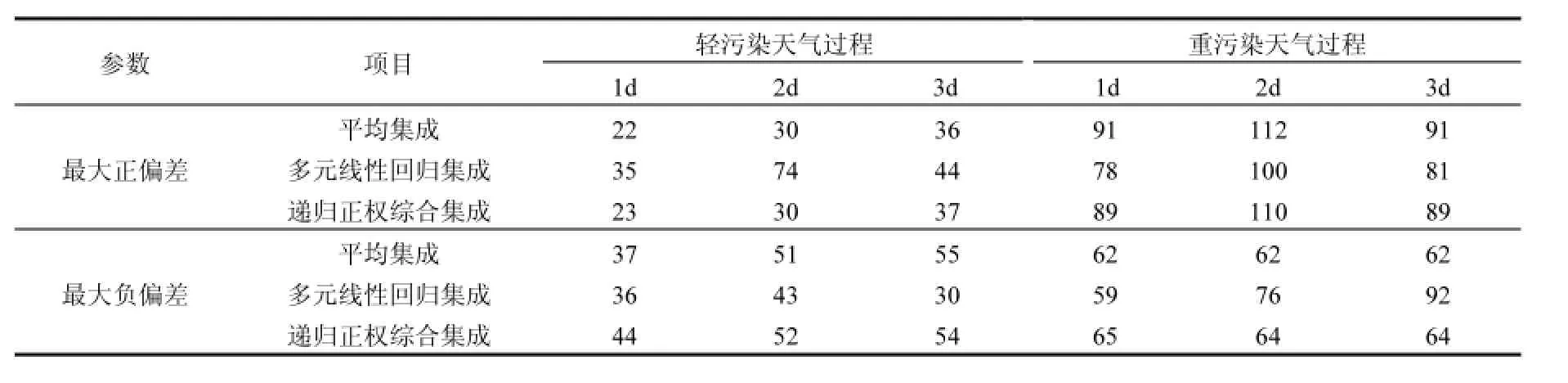
表2 3种集成模式的最大正负偏差(µg/m3)Table 2 Maximumpositive and negative deviation of three kinds of integration models (µg/m3)

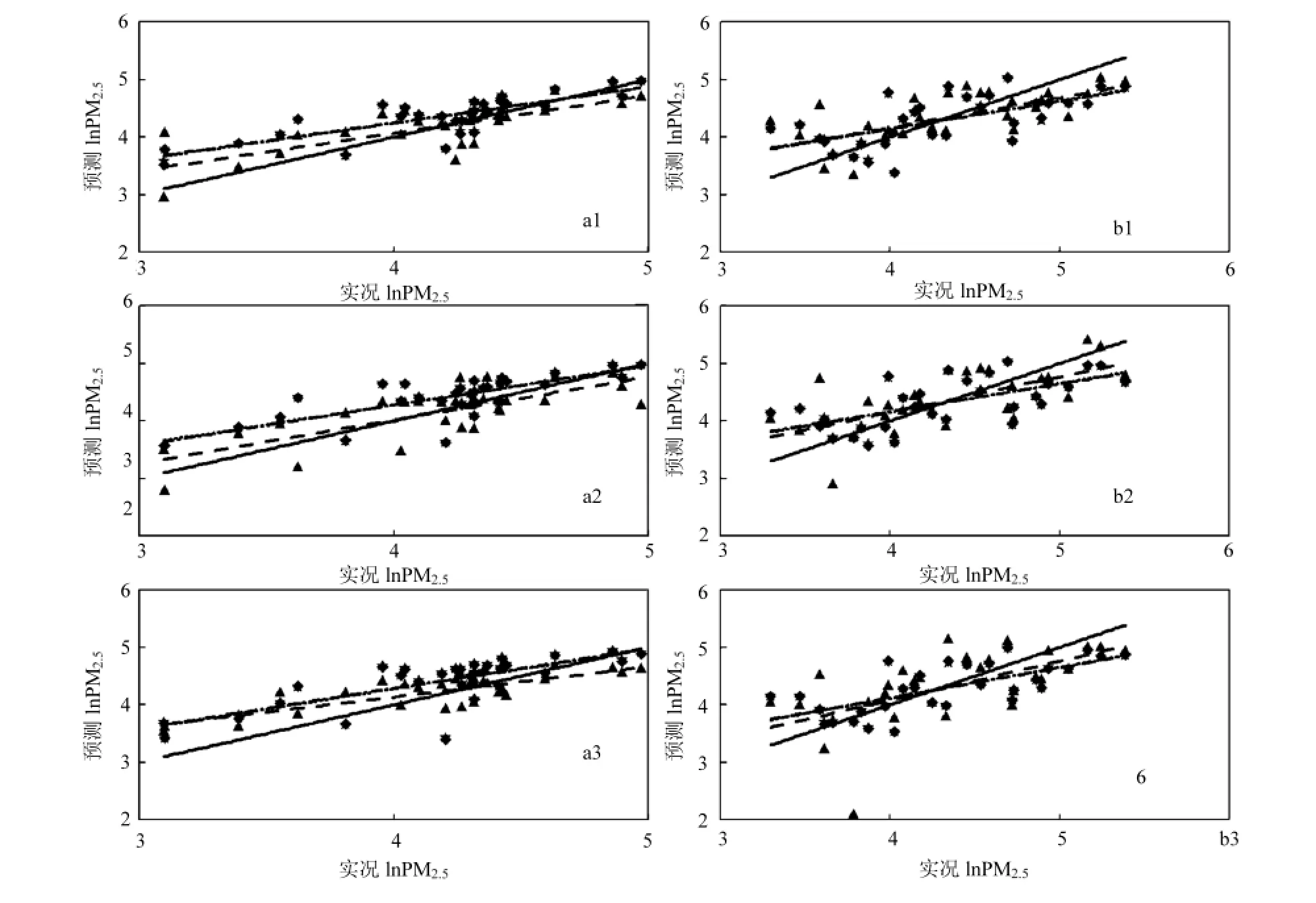
图2 上海市1d、2d和3d PM2.5日均浓度实测值与预报值的相关分析Fig.2 The correlation analysis of predicted values (Pre) and observed values (Obs) of PM2.5daily average concentration of the light pollution weather process based on the three MOS modes for one day (a1), two days (a2) and three days (a3) and the heavy pollution weather process for one day (b1) two days (b2) and three days (b3) in Shanghai

2.2.2 模式参数评价分析 首先本文对3种MOS模式和3种集成模式进行相关系数显著性检验,在0.01显著性水平上都显著相关.为了更好地考察3种集成模式的整体预报效果,本文通过相关系数(COR)、均方根误差(RMSE)和临界成功指数(CSI)评价参数对3种MOS模式和3种集成模式进行分析(表3).

从相关系数(COR)看,3种MOS模式中, WRF-RTIM模式对任意样本和时长的相关系数基本上最高;多模式平均和递归正权综合集成模式对任意样本和时长的相关系数基本上高于WRF-KALMAN和WRF-PLS模式,与WRFRTIM模式基本一致.而多元线性回归集成模式对于轻污染天气的任意时长均低于WRF-RTIM模式,对于重污染天气的任意时长均高于WRF-RTIM模式.总体来看,3种MOS模式对轻污染天气和重污染天气预报的相关系数分别集中在0.70～0.85和0.50～0.65之间,而3种集成模式对轻污染天气和重污染天气预报的相关系数分别集中在0.75～0.85和0.60～0.70之间.因此说明3种集成模式的整体趋势预报效果优于3种MOS模式,且对轻污染天气的趋势预报结果较好.

从均方根误差(RMSE)看,对于任意样本和时长,3种集成模式的均方根误差基本低于3种MOS模式,且多元线性回归集成模式的均方根误差最低.总体来看,3种MOS模式对轻污染天气和重污染天气预报的均方根误差分别集体在23～30μg/m3和39.5～43μg/m3之间,而3种集成模式对轻污染天气和重污染天气预报的均方根误差分别集中在19～24μg/m3和38～40μg/m3之间.因此说明3种集成模式的预报能力均优于3种MOS模式,且3种集成模式对轻污染天气的预报能力较好.

表3 3种MOS和3种集成模式预报值与实测值的统计参数分析Table 3 Analysis of statistic parameter for three kinds of MOS and three kinds of integration models predicted and observed values

从临界成功指数(CSI)看,在3种MOS模式中,WRF-RTIM模式对任意样本和时长的预报成功率都最高,3种集成模式对任何样本和时长的预报成功率均高于WRF-KARMAN和WRFPLS模式.对于轻污染天气和重污染天气1d、2d预报,多元线性回归集成模式的临界成功指数分别为90%、83%、87%和83%,高于WRF-RTIM模式;对于轻污染天气3d预报,3种集成模式的临界成功指数都低于WRF-RTIM模式;对于重污染天气3d预报,3种集成模式的临界成功指数都高于WRF-RTIM模式.总体说明,3种集成模式的整体成功率优于WRF-PLS和WRF-KALMAN模式,多元线性回归集成模式的整体成功率好于与WRF-RTIM模式.

本文不足之处:本文建模时仅考虑了地面气象条件对PM2.5污染物的影响,并未考虑高层气象条件对PM2.5污染物的影响;除此之外,本文将上海市看作一点,仅研究了上海市PM2.5日均浓度时间变化,并未考虑其空间演变特征.

3 结论

3.1 从预报值和实测值偏差看,3种集成模式对轻污染天气的预报多数时段高于实测值,对重污染天气的预报多数时段低于实测值,且多元线性回归集成模式的整体偏差低于另外2种集成模式,K-S和曼-惠特尼U检验也表明,多元线性回归集成模式的稳定性最好.

3.2 从均方根误差和相关系数看,3种集成模式的预报能力和整体趋势预报效果均优于3种MOS模式,其中多元线性回归集成模式的预报能力最优,且对轻污染天气的集成预报最优;说明3种集成模式对任意污染天气过程的预报能力都有所提升,且可有效降低决策风险.除此之外,3种集成模式对轻污染天气的预报能力和趋势预报均优于重污染天气预报,这也说明了重污染天气的预报难度较高.

3.3 多模式平均和递归正权综合集成模式的临界成功指数对任意样本和时长均好于WRFKALMAN和WRF-PLS模式,略差于WRF_ RTIM模式;多元线性回归集成模式的临界成功指数整体略好于3种MOS模式的.多元线性回归集成模式最优.

[1] Chan C K, Yao X. Air pollution in mega cities in China [J]. Atmospheric Environment, 2008,42(1):1-42.

[2] Huang C, Chen C H, Li L, et al. Emission inventory of anthropogenic air pollutants and VOC species in the Yangtze River Delta region, China [J]. Atmospheric Chemistry & Physics, 2011,11(9):4105-4120.

[3] Hu J, Wang Y, Ying Q, et al. Spatial and temporal variability of PM2.5 and PM10 over the North China Plain and the Yangtze River Delta, China [J]. Atmospheric Environment, 2014,95(1):598-609.

[4] Du X, Kong Q, Ge W, et al. Characterization of personal exposure concentration of fine particles for adults and children exposed to high ambient concentrations in Beijing, China [J]. Journal of Environmental Sciences, 2010,22(11):1757-1764.

[5] Qiu H, Yu I T, Wang X, et al. Differential effects of fine and coarse particles on daily emergency cardiovascular hospitalizations in Hong Kong [J]. A tmospheric environment, 2013,64:296-302.

[6] Zhang H, Xie B, Zhao S Y, et al. PM2.5 and tropospheric O3 in China and an analysis of the impact of pollutant emission control[J]. Advances in Climate Change Research, 2014,5(3):136-141.

[7] Pilinis C, Seinfeld J H, Seigneur C. Mathematical modeling of the dynamics of multicomponent atmospheric aerosols [J].Atmospheric Environment (1967), 1987,21(4):943-955.

[8] 房小怡,蒋维楣,吴 涧,等.城市空气质量数值预报模式系统及其应用 [J]. 环境科学学报, 2004,24(1):111-115.

[9] 欧阳琰,蒋维楣,刘红年.城市空气质量数值预报系统对PM2.5的数值模拟研究 [J]. 环境科学学报, 2007,27(5):838-845.

[10] Hubbard MC, Cobourn W G. Development of a regression model to forecast ground-level ozone concentration in Louisville, KY[J]. Atmospheric Environment, 1998,32(14):2637-2647.

[11] 谈建国,陆国良,耿福海,等.上海夏季近地面臭氧浓度及其相关气象因子的分析和预报 [J]. 热带气象学报, 2007,23(5):515-520.

[12] 周瑶瑶,马 嫣,郑 军,等.南京北郊冬季霾天PM2.5水溶性离子的污染特征与消光作用研究 [J]. 环境科学, 2015,30(6):1926-1934.

[13] Comrie A C. Comparing Neural Networks and Regression Models for Ozone Forecasting [J]. Journal of the Air & Waste Management Association, 1997,47(6):653-663.

[14] Lange N, Bishop C M, Ripley B D. Neural Networks for Pattern Recognition. [J]. Agricultural Engineering International the Cigr Journal of Scientific Research & Development Manuscript Pm, 1995,12(5):1235-1242.

[15] Cobourn W G, Dolcine L, French M, et al. A comparison of nonlinear regression and neural network models for ground-level ozone forecasting [J]. Journal of the Air & Waste Management Association, 2000,50(11):1999-2009.

[16] Kolehmainen M, Martikainen H, Ruuskanen J. Neural networks and periodic components used in air quality forecasting [J]. Atmospheric Environment, 2001,35(5):815-825.

[17] Feng X, Li Q, Zhu Y, et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation [J]. Atmospheric Environment,2015,107:118-128.

[18] 刘春霞,周家斌.用卡尔曼滤波预报南海热带气旋路径的试验[J]. 热带气象学报, 1997,13(4):349-356.

[19] 朱 江,汪 萍.集合卡尔曼平滑和集合卡尔曼滤波在污染源反演中的应用 [J]. 大气科学, 2006,30(5):871-882.

[20] D jalalova I, Monache L D, W ilczak J. PM2.5, analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model [J]. Atmospheric Environment, 2015,108:76-87.

[21] 朱红芳,王东勇.合肥市空气质量预报方法 [J]. 气象, 2002, 28(5):40-43.

[22] 许建明,徐祥德,刘 煜,等.CMAQ-MOS区域空气质量统计修正模型预报途径研究 [J]. 中国科学, 2005,35(A 01):131-144.

[23] Bian Lingen.北京城市大气环境污染机理与调控原理 [J]. 应用气象学报, 2006,17(6):815-828.

[24] 程念亮,李云婷,孙 峰,等.北京市空气重污染天气类型分析及预报方法简介 [J]. 环境科学与技术, 2015,38(5):189-194.

[25] Byun D W, Ching J K S, Byun D W, et al. Science A lgorithms of the EPA Models - 3Community Multiscale Air Quality (CMAQ) Modeling System[M]. Environmental Protection Agency Office of Research & Development, 1999.

[26] K rishnamurti T N, Kishtawal C M, LaRowT, et al. Improved Weather and Seasonal Climate Forecasts fromMultimodel Superensemble [J]. Science, 1999,285(5433):1548-1550.

[27] K rishnamurti B T N, K ishtawal C M, LarowT et al. Multi-modelSuperensemble Forecasts for Weather and Seasonal Climate [J]. Science, 2012,285(5433):1548-1550.

[28] Ebert E E. Ability of a Poor Man's Ensemble to Predict the Probability and Distribution of Precipitation [J]. Monthly Weather Review, 2001,129(10):2461.

[29] Mylne K R, Evans R E, Clark R T. Multi-model multi-analysis ensembles in quasi-operational medium-range forecasting [J]. Quarterly Journal of the Royal Meteorological Society, 2002, 128(579):361—384.

[30] Vijaya Kumar T S V, Krishnamurti T N, Fiorino M, et al. Multimodel Superensemble Forecasting of Tropical Cyclones in the Pacific [J]. Monthly Weather Review, 2003,131(3):574.

[31] 马 清,龚建东,李 莉,等.超级集合预报的误差订正与集成研究 [J]. 气象, 2008,34(3):42-48.

[32] 崔慧慧,智协飞.基于TIGGE资料的地面气温延伸期多模式集成预报 [J]. 大气科学学报, 2013,36(2):165-173.

[33] 张涵斌,智协飞,王亚男,等.基于TIGGE资料的西太平洋热带气旋多模式集成预报方法比较 [J]. 气象, 2015(9):1058-1067.

[34] 王自发,吴其重,A lex,等.北京空气质量多模式集成预报系统的建立及初步应用 [J]. 南京信息工程大学学报:自然科学版, 2009,1(1):19-26.

[35] 唐 晓,王自发,朱 江,等.北京地面O3的集合预报试验 [J].气候与环境研究, 2010,15(5):677-684.

[36] 黄 思,唐 晓,徐文帅,等.利用多模式集合和多元线性回归改进北京PM10预报 [J]. 环境科学学报, 2015,35(1):56-64.

[37] 陈焕盛,王自发,吴其重,等.空气质量多模式系统在广州应用及对PM10预报效果评估 [J]. 气候与环境研究, 2013,18(4): 427-435.

[38] 陆成伟,周来东,邓 也,等.基于Models-3的自修正空气质量预报系统及其效果检验 [J]. 中国环境管理, 2016,8(2):102-109.

[39] 徐文帅,李云婷,吴其重,等.AQI标准下北京市空气质量数值预报系统及其在重大活动保障中的应用 [J]. 中国环境监测, 2016,32(2):11-19.

[40] 佚 名.利用多模式集合和多元线性回归改进北京PM预报 [J].环境科学学报, 2015,35(1):56-64.

[41] Monache L D, N ipen T, Deng X, et al. Ozone ensemble forecasts: 2. A Kalman filter predictor bias correction [J]. Journal of Geophysical Research A tmospheres, 2006,111(D5):769-785.

[42] 尤佳红,束 炯,陈亦君,等.基于MOS的杭州秋冬季空气污染预报和霾诊断 [J]. 中国环境科学, 2014,34(7):1660-1666.

[43] 陈亦君,尤佳红,束 炯,等.基于WRF-RTIM的上海地区霾预报MOS方法研究 [J]. 环境科学学报, 2014,34(3):574-581.

[44] Cobourn W G, Dolcine L, French M, et al. A comparison of nonlinear regression and neural network models for ground-level ozone forecasting [J]. Journal of the Air & Waste Management Association, 2000,50(11):1999-2009.

[45] 谈建国,陆国良,耿福海,等.上海夏季近地面臭氧浓度及其相关气象因子的分析和预报 [J]. 热带气象学报, 2007,23(5):515-520.

[46] Einicke G A. Smoothing, Filtering and Prediction: Estimating the Past, Present and Future. Rijeka, Croatia: Intech [R]. ISBN 2012: 978-953-307-752-9.

[47] Forina M, Lanteri S, Kowalski B R. Chemometrics. Mathematics and Statistics in Chemistry [J]. NATO ASI Series, Ser. C, 1984, 138:439-66.

[48] GB 3095-2012 环境空气质量标准 [S].

致谢：李朝颐教授在论文撰写时提出宝贵意见;模式的数值计算在华东师范大学高性能计算机曙光5000上完成.

Comprehensive integration approaches for PM2.5statistical interpretation in shanghai.

LI Ya-yun1, SHU Jiong1*,SHEN Yu2
(1.Key Laboratory of Geographic Information Science, Ministry of Education, East China Normal University, Shanghai 200241, China；2.Shanghai Climate Center, Shanghai 200030, China). China Environmental Science, 2017,37(2)：486～496

The comprehensive integration approaches for statistical interpretation were employed to predict PM2.5concentration in Shanghai. Three kinds of model output statistics (MOS) models were built up by combining WRF model output with kalman filtering (KALMAN), partial least squares regression (PLS) and real-time iterative model (RTIM) respectively. And then three types of integrated model, based on MOS model above Multi-model average integration, recursive positive weight synthesis and multivariate linear regression integration, were separately apply to three days prediction for daily average concentration of PM2.5fromDec. 2 to 31, 2014 (light pollution process) and Dec. 15, 2015 to Jan. 13, 2016 (heavy pollution process). The prediction ability of pollution weather process for these integration models was improved by providing reasonable information and reducing the systematic errors in comparison with a single MOS models, which reduced the risk of decision-making in the process of pollution. The multivariate linear regression integration model presented higher precision and stability by comparative analysis of light and heavy pollution prediction processes. In all, the comprehensive integration approaches for statistical interpretation have great potential to be applied to regional air pollution prediction in operational model.

PM2.5；Multiple Linear Regression；integrated model；recursive positive weight synthesis；WRF

X513

A

1000-6923(2017)02-0486-11

李亚云(1991-),女,河南商丘人,华东师范大学硕士研究生,研究方向为大气污染模拟与控制.

2016-06-18

国家自然科学基金资助项目(41271055);国家社科基金重大项目(13&ZD161)

* 责任作者, 教授, jshu@geo.ecnu.edu.cn