基于试误理论的课堂教学策略

孟凡龙

试误理论是美国著名教育心理学家桑代克提出以解释学习实质与机制的一种方法.试误法又称尝试─错误法，是指消费者通过尝试与错误，从而在一定的情境和一定的反应之间建立起联结。试误理论的基本内涵是消费者在学习过程中，最初总是要经历一些错误的尝试动作，随着动作的不断反复，错误的动作逐渐减少，成功动作逐渐增多，最后完全获得成功。“种群的特征”是苏教版高中生物学教材《必修3·稳态与环境》第三章第一节“生物群落的基本单位—种群”的第一课时内容。本节教学中，笔者应用“以学生为主体，教师为主导”的探究性教学思想，引导学生通過一套教具亲自动手模拟样方法和标志重捕法等活动来学习种群的调查方法。试误理论在本节课中的具体实践主要体现在理解种群概念、学习样方法和标志重捕法时，不提供或提供少量知识背景，使学生在操作过程中出现理解误差和知识冲突。教师引导学生反思和总结，使学生形成比较科学完善的知识体系。

1 创设生活情境，导入新授课题

教师播放描述毛竹、帝王蝶、蜉蝣、旗鱼4种生物的1 min生活影片的微视频。

师：前面我们以个体的形式了解了动植物的调节和稳态的维持，那么很多个体在一起会是怎样的群体呢？这样的群体会有怎样的特征？它们又是如何维持稳态的呢？

师：同学们看到影片中有哪些生物？（请一位学生回答）这些生物是以个体形式还是群体形式生活？（学生齐答）我们给这样的生活在一定区域的同种生物的所有个体的集合起个名字，叫什么呢？（种群）

过渡：通过对种群知识的学习，为森林树木的合理砍伐、池塘鱼类的合理捕捞、草原牛羊的合理放牧的解释提供科学的依据。

2 联系生产实际，把握核心概念

师：首先，根据讨论，我们请一位同学给种群下个定义。（请一位学生回答，教师修正，得出完整的种群的定义）那么，该定义中的关键词是什么？（请一位学生回答，并根据关键词举例）

教师投影图文表述（① 一片草地上所有的草；② 两个池塘中的鲤鱼；③ 一块棉田中由幼蚜、成熟蚜等组成的全部棉蚜；④ 一个蜂窝里全部的雄蜂），请同学判断哪一个是种群，并说明理由。

师（过渡）：看到图中的一个种群中有这么多的个体，我们就想知道，这个种群中到底有多少个体？首先请同学们比较哪个草地的蒲公英数量多？

教师投影：甲草地10 m2有400株蒲公英，乙草地100 m2有3 000株蒲公英。教师引导学生分析数据，得出种群密度的概念，同时以池塘中的鲫鱼为例，进一步完善种群密度的概念。教师指出：种群密度是种群最基本的数量特征。引导学生理解：要得到某种群密度，就先要知道该种群所有个体的数量和该种群所占据的面积或体积。

师：那么种群数量如何调查呢？投影：1 m2草地中的蒲公英数量（图1），请同学们计算该地区蒲公英的种群密度。

有学生得出21株/ m2，也有22株/ m2。教师引导学生比较后得出：差异在于边界上的个体如何计数。有的学生认为是随便取两边计数，有的学生认为是边界上的所有个体都算。根据学生的想法，教师反问：你们觉得哪种计数更加科学合理？引导学生分析：该地区由于蒲公英数量较少，所以可以直接计数，那么边界上的个体我们一般取相邻两边及其夹角上的个体计数，比如我取左边和上边及其夹角的个体计数，就得到了21株/ m2，或者取右边和下边及其夹角的个体计数，就得到了22株/ m2，都是科学有效的。

师：那么，对于分布范围较大、个体较小、数目较多的种群，无法直接计数时，如何调查种群密度呢？（引导学生采用估算的方法）

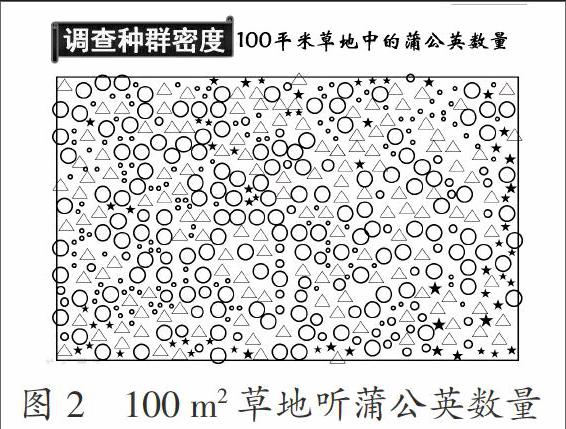
教师简单介绍估算法：估算是一种重要的科学方法，在生产生活中应用很广泛，估算肯定会有误差，如何尽可能地减少误差，使数据更加科学合理有效是估算法的关键。所以调查100 m2草地中的蒲公英种群密度（投影图2）时就要选取有代表性的地方，即样方。

师：首先请同学们带着几个问题讨论交流：① 样方的面积多大更适宜？② 选取多少个样方更合理？③ 在图2中的什么位置选取样方更科学合理？④ 边界上的个体如何计数？

学生讨论交流，请小组代表回答。教师引导学生理解选取样方的重要原则是随机，并逐步展示五点取样法和等距取样法，引导学生选择更加科学合理的随机取样方法：避免偶然性带来的误差。边界上的个体选择相邻两边及其夹角的个体计数，注意每个样方计数的相邻边界应该是相同的，如每个样方都选择左边和上边及其夹角的个体计数。

3 主动参与模拟，探究活动本质

师：那么，我们可以模拟样方法进行随机取样吗？需要提供哪些材料？

学生讨论交流，教师补充，并展示教具：信封1中的若干黄豆、含有25个标号方格的白纸盘（图3）。教师指出实验目的是估算出信封1中的黄豆数量。各小组分组讨论，并实施，同时在导学案的表格中记录每个样方法的黄豆数量。

学生进行模拟活动，有的小组将黄豆随机撒到白纸盘中，有的小组将黄豆倒入白纸盘中后再摇动白纸盘使黄豆分布均匀，有的小组将所有黄豆集中到白纸盘一边的5个方格中。教师要求每个小组将选取的样方中的黄豆数量计算平均值，然后每小组派一位同学将本组的样方平均值输入到图4的“样方平均值”文本框（已经插入了文本框控件，学生可以直接在演示的幻灯片上输入数字）中。

每个小组输入完毕后，教师设问：我们已经知道了各小组的每个样方的黄豆数量平均值，那么各小组的信封1中的黄豆总数如何计算？

学生回答：再乘以25即可。教师点击相应的“种群总数量”文本框[已经设置了相应的代码Private Sub TextBox2_MouseDown（ByVal Button As Integer， ByVal Shift As Integer， ByVal X As Single， ByVal Y As Single）；TextBox2.Text = Val（TextBox1.Text） * 25；End Sub]，得到每个小组的黄豆总数。然后，教师指出最接近真实值的小组（不说出黄豆的真实数量，为后续实验做准备）和最偏离真实值的小组。先请最偏离真实值的小组代表阐述本组的操作流程，然后再请最接近真实值的小组代表阐述，教师及时引导学生分析：每组模拟实验过程中是否严格遵循了随机原则？选取的样方是否具有代表性？是否注意到样方的个数、边界上的个体计算、黄豆的分布情况等造成的实验误差？

师（过渡）：刚才同学们在选取好样方后计算黄豆数量时，要注意什么？

教师要求一位学生回答，引导学生理解：黄豆是圆形的，不能滚动，否则无法计数。因此，样方法适合于调查什么样的生物的种群密度？

教师引导学生分析：样方法可以用来调查植物和活动能力弱、活动范围小的昆虫卵、蚜虫、跳蝻等动物。那么活动能力强、活动范围大的其他动物如何调查呢？并要求学生自主学习教材相关内容。

教师要求一名学生描述标志重捕法的原理，并提出问题标志重捕法在实际野外调查中怎样进行呢？

教师展示例题：在一块面积为2 hm2农田中，放置100个捕鼠笼，一夜間捕获了42只田鼠，将捕获的田鼠经标记后在原地释放。数日后，在同一地点再放置同样数量的捕鼠笼，捕获了37只，其中有上次标记的个体12只。则该农田中田鼠的种群密度为 。

教师要求一名学生板演计算过程，并分析标记技术要求，以引导学生理解：标记物不能影响被标记动物的正常活动，不能导致其生病、感染等；不能过分醒目，影响捕食关系；标记符号能维持一定时间，至少调查期间不能消失。同时请学生分析：如果影响了标记动物的生命活动，其调查得到的种群密度会偏大还是偏小？过分醒目了呢？标记物脱落了呢？

师：那么，我们可以模拟标志重捕法估算动物数量吗？需要提供哪些材料？

学生讨论交流，教师完善，并展示教具：信封1中的若干黄豆、信封2中的若干红豆。教师指出：信封1中的若干黄豆模拟某鱼塘中的鲫鱼，信封2中的若干红豆用来作为标记，实验目的是估算出信封1中的黄豆数量。

各小组分组讨论，并实施，同时在导学案的相应表格中记录M、n、m的值（图5）。

教师请速度最快的四个小组的代表选择一次标志重捕的数据填写到相应小组的文本框中。教师点击相应的文本框[已经设置了相应的代码，如第一小组的第4个文本框代码为Private Sub TextBox4_MouseDown（ByVal Button As Integer， ByVal Shift As Integer， ByVal X As Single， ByVal Y As Single）；TextBox4.Text = Val（TextBox1.Text） * Val（TextBox2.Text） / Val（TextBox3.Text）；End Sub]，得到每个小组的黄豆总数。然后，教师指出最接近真实值的小组（不说出黄豆的真实数量，为后续实验做准备）和最偏离真实值的小组。先请最偏离真实值的小组代表阐述本组的操作流程，再请最接近真实值的小组代表阐述，教师及时引导学生分析如何减少实验误差，如标记的个数、重捕的个数、抓取的次数、搅拌的程度等。同时，提出拓展问题：你还可以用生活中的哪些材料完成该模拟活动？并尽可能地减少实验误差。

教师总结本节课学习的种群密度的调查方法及其注意事项，指出：种群密度是种群最基本的数量特征，种群还有很多的其他特征，课后可以将种群和个体的特征进行比较。

教师布置课后延伸：你能尝试设计，并小组合作调查美丽校园中的一种植物的种群密度吗？

4 教学反思

本节课注重联系现实生活来激发学生的学习兴趣，理解核心概念，教学过程中突出学生的学习主体，在试误理念的引领下让学生通过尝试错误来寻找解决问题的关键点。教师教学中创造性地运用一种模拟材料完成了两种模拟实验的操作，通过学生自主模拟样方法和标志重捕法的活动，引导学生分析，从而生成更加科学合理的模拟实验步骤。在自主探究和自主活动中形成知识冲突，在讨论交流中不断修正自己的知识体系，让每一位学生有展示自己的机会，并设计小组间的竞争机制，充分调动学生的学习热情。