考虑临近空间零控交班的指令修正中制导研究
张浩强, 唐胜景, 郭杰, 刘骁, 徐倩
(1.北京理工大学 宇航学院 飞行器动力学与控制教育部重点实验室, 北京 100081; 2.北京宇航系统工程研究所, 北京 100076)
考虑临近空间零控交班的指令修正中制导研究
张浩强1, 唐胜景1, 郭杰1, 刘骁1, 徐倩2
(1.北京理工大学 宇航学院 飞行器动力学与控制教育部重点实验室, 北京 100081; 2.北京宇航系统工程研究所, 北京 100076)
针对临近空间高超声速目标防御问题,根据目标特性提出了空基巡航段防御方案。在此基础上考虑临近空间防御特点进行中末制导交班问题分析,提出交班点性能指标,并得出连接中末制导阶段的有效零控拦截交班区域(零控交班)。结合模型预测静态规划理论与防御飞行器中制导终端状态约束条件,推导了最优控制问题的解析算法并将其作为防御飞行器的指令修正制导律,针对不同任务情况进行了数值仿真。仿真结果表明,零控交班区域分析结果可满足终端小速度比交会条件。设计的中制导律在显著提高计算效率的同时满足零控交班约束,且经过Monte Carlo仿真表明对初值扰动具有较强的鲁棒性。
兵器科学与技术; 飞行器设计; 零控脱靶量; 交班点; 模型预测静态规划; 中制导
0 引言
临近空间是指传统的航天与航空之间的空白区域,一般认为在20~100 km之间的空间领域。近年来,临近空间特殊的战略价值已经得到广泛重视[1]。随着临近空间飞行器的快速研究与发展,临近空间已成为国家空间战略安全的重要组成部分[2]。因此,对临近空间目标有效防御的研究具有重要的战略意义。本文考虑的高超声速飞行器是在临近空间某高度以较稳定的速度飞行并具有一定滞空时间的巡航型飞行器,这类飞行器主要指近年来发展的吸气式高超声速巡航飞行器[3]。
吸气式高超声速巡航飞行器在其巡航段飞行时间最长,攻击窗口最大,航迹最平稳,最容易被发现和跟踪,因而巡航段防御是一种最有效、最理想的目标交会方式[4]。根据文献[5]提出的空基发射防御方案,本文系统地研究了临近空间防御飞行器中制导框架中存在的问题。
空基防御飞行器是基于成熟的中远程空空导弹改进而成:在预警系统发现并跟踪目标后,载机携带防御飞行器迅速爬升至一定高度。此后防御飞行器发射,爬升至目标高度后对目标进行攻击。对于此类空基防御飞行器,在导引头开机前自身无法锁定目标,所以需要采用复合制导体制来完成目标打击任务。
其交班点作为中制导结束点同时也是末制导启控点,对于防御飞行器的复合制导体制起到了承前启后的关键作用。文献[6-7]从理论上研究了反临近空间高超声速飞行器中末制导交班需用的导引头关键技术及视角选择问题。在针对考虑临近空间防御特点的中末制导交班点分析方面,国内外的相关文献目前较少,并且多集中于对导引头技术的研究,缺乏对最佳交班位置及相关约束条件的详细讨论与分析。
对于中制导体制的选取,本文选用空空导弹普遍采用的捷联惯导+雷达指令修正中制导方案[8-9]。在防御飞行器中制导阶段,针对高超声速目标的时敏性,在线可实时优化的制导段轨迹生成算法已经成为当前研究的热点与难点[10]。针对这一问题,本文考虑采用一种快速可在线实施的制导律作为修正指令,并由火控系统通过数据链实时控制飞行器轨迹。因此对此种修正制导指令进行设计与验证,则成为临近空间防御飞行器中制导框架中的又一个关键问题,亦作为本文的另一个研究重点。
最优控制理论被广泛应用于制导律框架设计,包括针对高速来袭目标的最优指令成形制导律及带多约束条件的时变参数次优中制导律研究等[11-12]。近年来,Padhi等[13]将模型预测控制(MPC)与近似动态规划(ADP)相结合,提出了模型预测静态规划(MPSP)理论。对于最优控制中的典型两点边值问题,该方法只需要静态协态矢量来更新控制量,且协态矢量可以通过使用敏感度矩阵来进行递归计算。目前MPSP理论已经应用到飞行器再入制导[14]、高速目标防御中制导[15]以及带落角约束的末制导[16],具有较好的应用价值和发展前景。
针对上述背景与问题现状,本文考虑采用空基防御方案。在此方案背景下,考虑临近空间高超声速巡航飞行器飞行特点,并基于零化末制导零控脱靶量(ZEM)的设计思想,本文对中末制导零控交班区域进行讨论分析;同时给出了相应的弹道及动力学约束;结合MPSP理论方法,对考虑多终端约束的指令修正中制导律进行了设计研究。
1 中制导模型
1.1 目标巡航段弹道特性分析
针对高超声速目标,如前所述,其在巡航段飞行过程中有非常明显的弹道特性,在此段进行防御拦截最为有效:
1)典型高度飞行。由于低空大气密度大使得阻力较大,而过高的飞行高度又不能给发动机提供足够的空气,采用吸气式超燃冲压发动机的高超声速飞行器,由于飞行攻角的约束限制,较适合于在约30 km高度巡航飞行。
2)临近空间内的飞行时间较长。
3)高超声速巡航飞行。
4)机动力较弱。临近空间气体稀薄,导致可用过载相对较低,尤其是吸气式冲压发动机的进气道设计限制了其大攻角飞行,而巡航段的飞行器也不易实现直接力控制[5]。
1.2 弹目相对非线性运动学
弹目相对非线性运动学多建立在惯性参考坐标系下,如图1所示。图1中:r为导弹与目标之间的相对距离;λ为弹目视线角;v、a、γ、Φ分别表示速度、加速度、弹道倾角以及速度前置角,下标M、T分别表示导弹与目标。其运动方程为
(1)
式中:vr与vλ分别表示弹目相对速度沿弹目视线的切向分量与法向分量。

图1 非线性运动学弹目关系Fig.1 Relationship between missile and target in nonlinear kinematics
1.3 中制导段防御飞行器数学模型
防御飞行器纵向平面的质点动力学模型(不考虑发动机推力)为
(2)
式中:xM、yM为防御飞行器在发射坐标系中的位置;D为气动阻力;ηγ为制导指令;g为重力加速度;m为防御飞行器质量。
2 临近空间防御中末制导交班问题分析
2.1 常规交班点性能指标分析
从制导的最终目的来看,控制终端时刻的脱靶量达到最小是末制导的一个非常重要的指标。而中末制导交班点为中制导与末制导的承接点,既作为中制导的终止点也作为末制导的启控点,因此这一点处的弹道特点以及性能指标显得尤为重要,对整个制导过程来说都起到了承前启后的关键作用。
由于发动机和其他技术水平的限制,为了让导弹具有一定的射程,必须考虑在长时间的中制导过程中使导弹能量消耗尽可能的少。另外,在采用惯性制导方式时,中制导过程中导弹不再获取目标信息,这将使得不可预计的目标机动随时间逐渐累积。在这种情况下,需要把短的飞行时间作为中制导的一个基本性能指标。
2.2 考虑临近空间防御特点的交班点性能指标分析
1)速度约束。定义临近空间防御飞行器在中末制导交班时刻的速度大小为vM,临近空间高超声速飞行器的巡航速度大小为vT,则二者速度比为:η=vM/vT,并且η一定小于1. 将这种情况定义为小速度比攻击。同时,出于对末制导过程中机动能力的考虑,希望在交班点处防御飞行器能拥有较大的终端速度。
2)高度约束。假设在中末交班时刻弹目速度比η一定,即防御飞行器速度大小一定。在这一时刻从能量角度分析,相对于某一水平面,若防御飞行器位置高于高超声速巡航飞行器的位置,那么在弹目终端交汇时刻防御飞行器有一部分势能可以转化为动能,形成俯冲攻击从而可提供更大的可用过载。从另一个角度分析,文献[7]研究得到的结论指出:为提高导引头探测距离,从而增加末制导作用距离,探测视角最好采用自上而下的方式。同样也对交班点高度约束提出了要求。
3)ZEM约束。ZEM的概念最早被应用于防御大气层外处于自由飞行段的弹道导弹[17-19]。ZEM的物理意义是导弹从当前时刻到制导结束不再输出制导指令,而目标仍按此前的机动方式运动,弹目直至终端时刻的脱靶量大小。本文提出零化交班时刻ZEM的思想,将交班点处的ZEM作为中制导的一个终端约束。
根据图1所示的非线性运动关系,定义弹目相对位移矢量为R,相对速度矢量为v,v与R叉乘的模ε为零控脱靶标志量,其中δ为v与R的夹角,零控脱靶标志量的数学推导为
v×R=0,
(3)
ε=|v×R|,
(4)
ε=|v||R|sinδ=vλR.
(5)
2.3 有效零控拦截交班区域
本节主要针对提出的有效零控交班区域给出具体的分析推导过程,并据此给出相关概念的定义。为便于分析推导,作以下假设:
1)对于临近空间高超声速巡航目标,预警探测系统可以探测到目标的航迹点,包括航迹点位置及目标速度;
2)仅考虑防御飞行器与目标在同一纵向平面内的质心动力学情况,同时认为防御飞行器攻角α≈0°;
3)探测到航迹点的时间间隔均匀,探测周期为T;
4)tn时刻探测到的目标信息为Xn=(xn,yn,zn),根据Xn可以预测下一时刻的目标信息Zn+1,并将tn+1作为末制导的启控时刻;
5)如果目标在一个探测周期内发生了机动,那么在tn+1时刻进行重新探测得到该时刻的实际探测值Xn+1,并将该时刻预测的下一时刻目标信息Zn+2作为末制导的启控点;
6)目标速度方向与参考平面平行,即弹目视线角λ与目标前置角ΦT相同。
7)防御飞行器导引头最大探测距离为rmax,导引头视场角为ψ(假设导引头光轴不转动)。
交班时刻的弹目相对位置关系如图2所示。其中,点O1为tn+1时刻预测到的目标航迹点位置,以O1为圆心以rmax为半径作圆O1,圆O1表示在tn+1时刻目标可被捕获的最大范围;O1O2表示目标当前时刻的速度矢量,以目标速度矢量的终点O2为圆心,以防御飞行器速度大小vM为半径做圆O2(则圆O2上任意一点与点O1、点O2构成闭合的弹目速度矢量三角形);O1A和O1B分别为圆O2过点O1的两条切线。

图2 零控交班区域Fig.2 Zero effort handover region
根据文献[20]对零控拦截的定义及本文提出的假设1~假设7,结合图2对零控交班区域展开推导与分析如下:

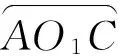
ΦM=arcsin (sinλ/η),
(6)
γM=-(ΦM+λ)=-arcsin (sinλ/η)-λ;
(7)
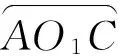
5)根据图2中几何关系可知,在最大零控交班区域范围内,对于不同的中、末制导交班点位置处的速度前置角会随着弹目视线角的减小而逐渐减小。
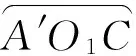
(8)
由(8)式可知,影响有效零控交班区域的主要因素有两点,分别为弹目速度比和导引头视场角的大小。在一定范围内,适当增大弹目速度比或者提高导引头视场范围,可以一定程度上增大有效零控交班区域。
另外,在考虑纵向平面质点模型的条件下,认为导引头视场范围即为视场锥体在参考线上投影的长度lp. 因此有效零控交班区域内不同的点会对应不同的投影长度,考虑以O1为极点的极坐标系,对有效零控交班区域内任意有限点进行曲面拟合,则有
lp=f(r,λ).
(9)
由有效零控交班区域所得的中制导终端约束条件对防御飞行器位置的约束应该是一个点。因此,曲面函数f(r,λ)的极大值点即为最佳交班位置。
3 防御飞行器中制导终端约束
中制导终端约束的确定,首先需要根据第2节的分析计算零控交班区域内不同点作为交班点时的视场投影长度,并选取投影长度极大值为最佳位置,从而以该点的动力学状态作为终端约束,最后将该点的位置和速度信息转换到防御飞行器发射坐标系下即可。
如图3所示,I为末制导交班点,ri和λi分别表示ti时刻的弹目距离和弹目视线角度,hi表示当前时刻防御飞行器相对于目标的高度,li表示防御飞行器视场在这一高度参考线上的投影长度。
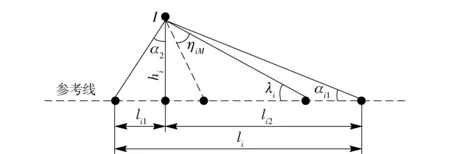
图3 视场投影长度Fig.3 Projected length of field of view
根据图3的几何关系及(8)式可得
li=f(ri,λi),
(10)
li=li1+li2=hitanα1+hi/tanα2,
(11)
式中:
hi=risinλi;
(12)
αi1=ψ/2+λi+ηiM-π/2;
(13)
αi2=λi+ηiM-ψ/2.
(14)
将(12)式~(14)式代入(11)式中整理可得
(15)
通过分析(15)式的极大值点(rd,λd)来确定最佳交班位置:根据(5)式的单调性可知随着λ的逐渐减小,ηM也逐渐减小;弹目视线变化过程中的某一个位置会出现极限情况lp=∞,即防御飞行器视场一条边界与参考线平行;如果弹目视线角继续减小,防御飞行器高度下降但投影长度仍维持无穷大。
综合以上分析并考虑防御飞行器高度约束,弹目视场边界恰好与参考线平行的位置为最佳交班位置,即
(16)
极坐标(rd,λd)转换成发射坐标(xd,yd)有
(17)
式中:(xT,yT)为目标在发射系下的坐标位置。
根据平行原理可得弹道倾角γd=-ψ/2,那么,Xd=[xd,yd,γd]T即为中制导结束时所需满足的终端约束条件。
4 MPSP方法
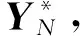
Xk+1=Fk(Xk,Uk),
Yk+1=h(Xk),
(18)
式中:X为状态变量;U为控制变量;Y为控制输出,控制目标满足MPSP理论的基本原理。
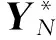
(19)
(20)
式中:HOT为高阶小量。
根据(18)式,第k+1步的状态量误差为
(21)
将(21)式带入(20)式可以得到第N步的输出误差为
(22)
继续按照(21)式中的形式展开(22)式中的dXN-1,得
(23)
以此方式迭代求解得
dYN=AdX1+B1dU1+B2dU2+…+
BN-1dUN-1,
(24)
式中:
(25)
Bk称为敏感度矩阵,由于在第1步迭代时初值已经给定,因此不存在状态误差量,即(24)式中dX1=0,则
(26)
这里需要注意,在推导(26)式的过程中,假设每一步的控制变量都独立于前一步的状态量与控制输入。
由(25)式可知,敏感度矩阵的计算相当繁琐,这将会大大影响MPSP算法的求解效率,但可以注意到,敏感度矩阵可以通过下面的推导进行反向递归求解:
(27)
(28)
根据(26)式及最优控制的ADP方法,文献[11]给出了控制指令更新算法,本文直接给出最终结论:
(29)
(30)
式中:Rk为正定系数矩阵。
5 MPSP指令修正中制导律设计
本文基于零控交班区域分析并根据MPSP理论方法,对空基临近空间防御飞行器进行指令修正中制导律设计。
在对质心动力学模型(2)式的求解中,时间作为独立自变量,因此需要知道中制导全程时间并沿时间正向积分。本文为避免对剩余飞行时间的估计,选取防御飞行器位置坐标x作为动力学模型的独立自变量。
(31)
对模型(31)式采用欧拉法进行离散化处理:
Xk+1=Fk(Xk,Uk),
(32)
式中:
(33)
由x方向终端位置xd可计算离散步长为
(35)
(36)
式中:yf、γf分别为终端时刻的y方向位置和弹道倾角。
根据(27)式~(30)式可计算更新制导指令:
(37)
6 仿真研究
本节通过仿真比较以检验本文所设计的制导律对不同情况的适应性能。采用离散化的非线性动力学模型(32)式进行仿真研究,仿真初始条件及部分参数见表1. 其中,参考坐标系选取与图1中相同,定义防御飞行器初始位置为坐标原点。
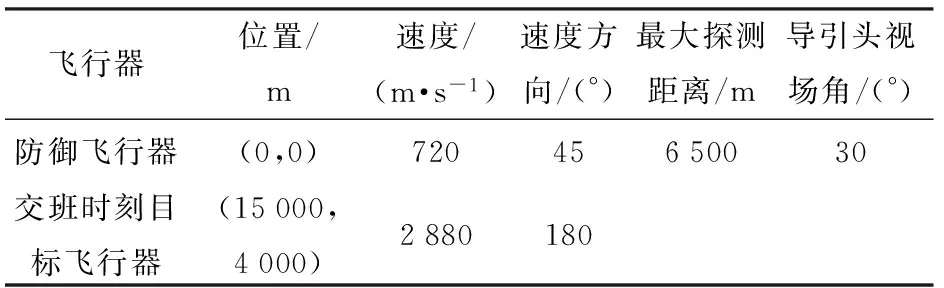
表1 仿真初始参数Tab.1 Initial simulation parameters
根据表1及(16)式和(17)式计算不同末制导弹目速度比下的期望交班位置,计算结果见表2.

表2 不同速度比下的期望交班位置Tab.2 Desired handover locations at different velocity ratios
6.1 制导律性能校验
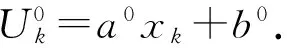
1)a0=-0.2,b0=1,η=1/4;
2)a0=-0.4,b0=1,η=1/4;
3)a0=-0.2,b0=1,η=1/5.
算例的仿真结果分别如图4~图6和表3~表5所示。
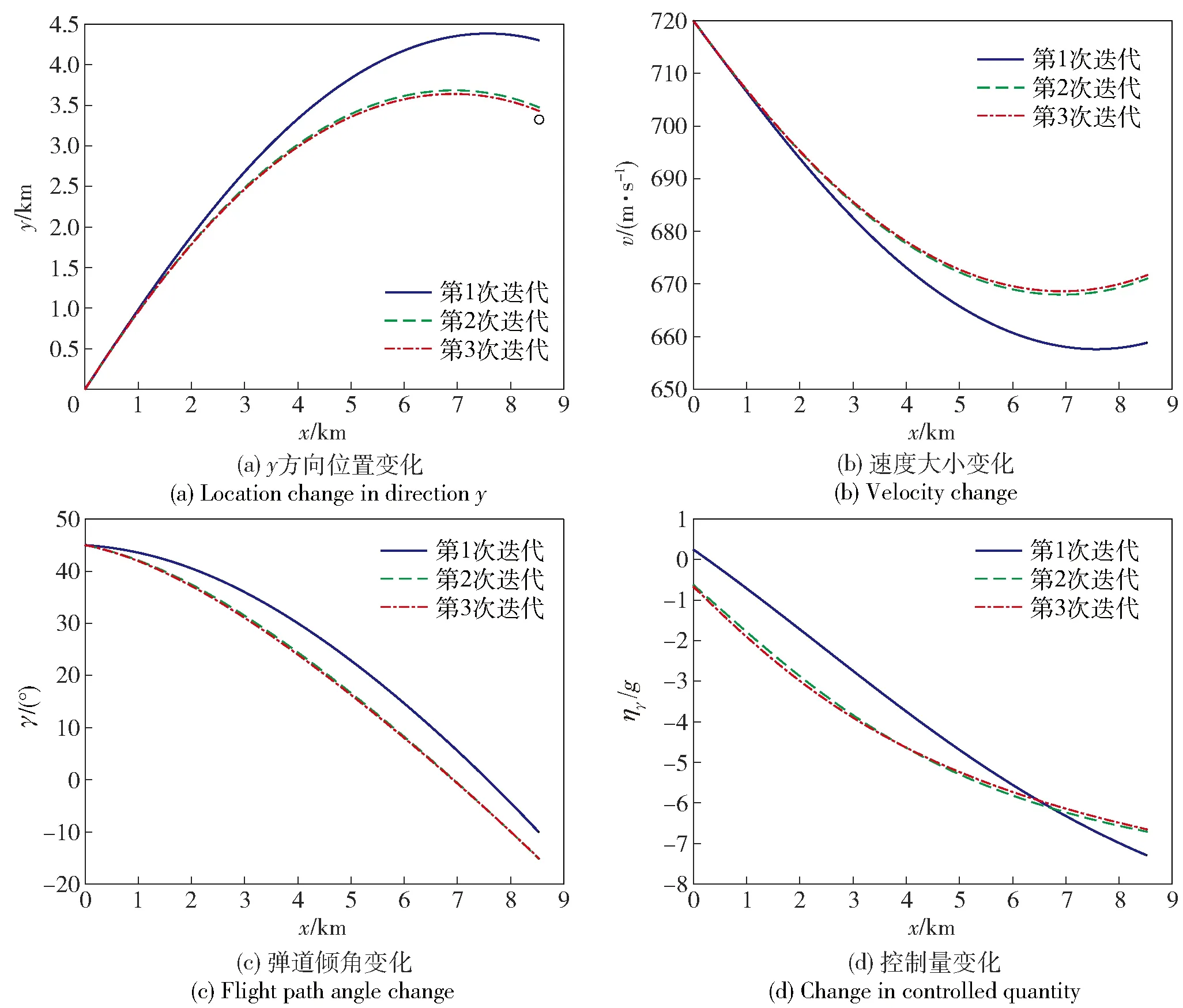
图4 算例1多次迭代后的仿真结果Fig.4 Simulated results of Example 1 after multiple iterations
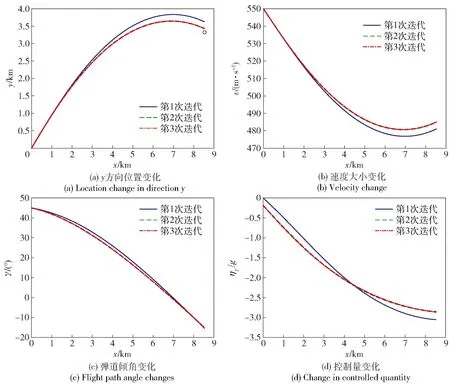
图6 算例3多次迭代后的仿真结果Fig.6 Simulated results of Example 3 after multiple iterations

表3 算例1终端误差Tab.3 Terminal errors of Example 1

表4 算例2终端误差Tab.4 Terminal errors of Example 2

表5 算例3终端误差Tab.5 Terminal errors of Example 3
比较算例1与算例2可知,在弹目速度比一定的前提条件下,本文设计的制导律对控制初值猜测不敏感。对比表3与表4所得仿真数据,可以看出针对相同的期望交班位置,随着制导律逐步迭代,制导终端误差逐渐减小;并且不同的控制指令初值均可使终端误差在3步后基本收敛。
综合比较仿真算例1~算例3,初始控制指令都选用自变量的线性形式,针对不同的弹目速度比及控制指令初值,基于MPSP算法设计的中制导律均可保证导弹最终达到期望的中末制导交班位置,并满足相应的终端角度约束。
6.2 制导律鲁棒性校验
本文通过对初始状态进行扰动来对所设计制导律的鲁棒性进行评估。初始状态偏差的变化范围设定为
(38)
在(38)式所确定的初始扰动变化范围内,采用Monte Carlo方法对制导方法进行效果验证。分别对不同的初始位置偏差及初始弹道倾角偏差进100次仿真计算,这里Monte Carlo仿真初值选择与6.1节算例1相同。
由于本文并未对终端速度进行约束,因此不考虑对速度的初始扰动进行仿真。图7及图8中曲线表示在初始状态存在扰动情况下,本文所采用的制导律依旧可以使扰动弹道有效收敛于预期位置,并满足相应落角约束。
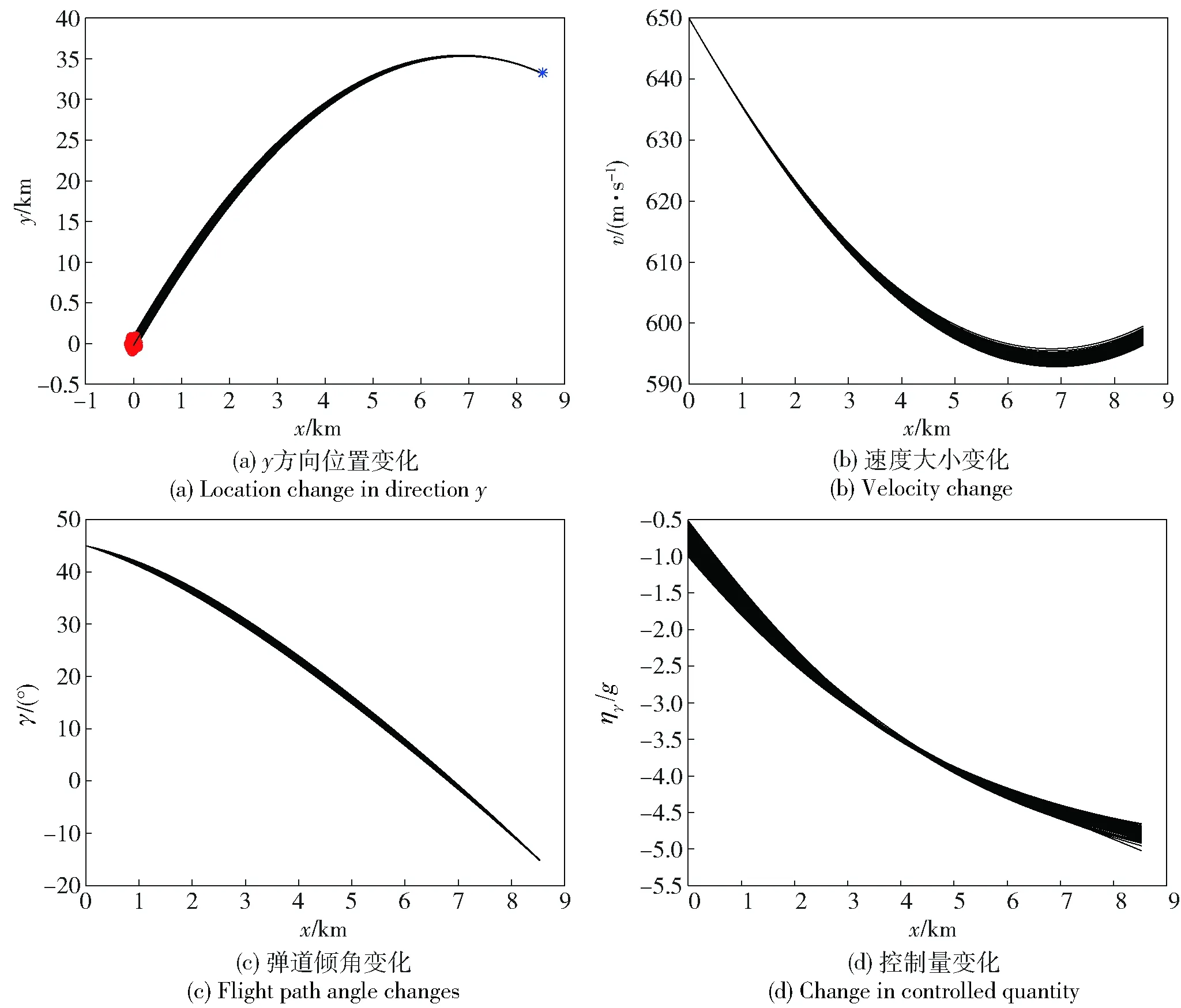
图7 考虑初始位置误差的Monte Carlo仿真结果Fig.7 Monte Carlo simulation results in considering the initial location error
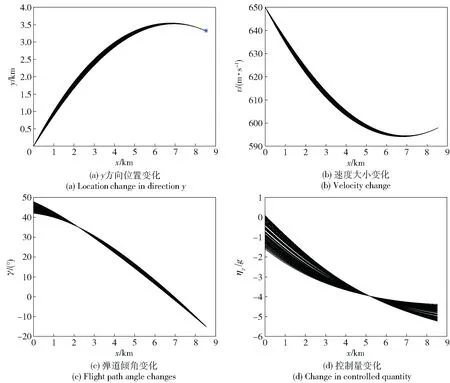
图8 考虑初始角度误差的Monte Carlo仿真结果Fig.8 Monte Carlo simulation results in considering the initial angle error
7 结论
本文利用零化ZEM思想,对中末制导交班区域进行分析,结论得出了临近空间防御飞行器中末制导最佳交班位置。应用MPSP理论对考虑交班区域终端约束的指令修正中制导律进行设计。仿真结果表明设计的制导律可以对交班区域进行精准覆盖,并能满足位置、角度等终端约束,并且制导律对初始猜测控制指令不敏感。同时,在临近空间防御飞行器中制导初始状态受到扰动情况下,设计的中制导律仍旧可以有效完成本文提出的中末制导零控交班任务。
由于制导律控制指令更新为解析形式,并且对于不同仿真情况终端误差在迭代3次后基本收敛,因此将该制导形式作为修正指令,可较为快速准确地应对临近空间目标机动,在一定程度上满足在线制导需求。同时基于MPSP理论的设计方法对在线闭合制导律研究方面同样具有很大的应用前景。
References)
[1] 黄伟, 罗世彬, 王振国. 临近空间高超声速飞行器关键技术及展望[J]. 宇航学报, 2010, 31(5):1259-1265. HUANG Wei, LUO Shi-bin, WANG Zhen-guo. Key techniques and prospect of near-space hypersonic vehicle[J]. Journal of Astronautics, 2010, 31(5):1259-1265.(in Chinese)
[2] 呼卫军, 周军. 临近空间飞行器拦截策略与拦截武器能力分析[J]. 现代防御技术, 2012, 40(1):11-15. HU Wei-jun, ZHOU Jun. Analysis of the interception strategy of the near space vehicle and capability of the interception weapon [J]. Modern Defense Technology, 2012, 40(1):11-15. (in Chinese)
[3] Marcel M J, Baker J. Interdisciplinary design of a near space vehicle[C]∥Proceedings of Southeast Conference. Richmond, VA: IEEE, 2007:421-426.
[4] 王还乡, 李为民, 上官强, 等. 高超声速飞行器巡航段拦截作战需求分析[J]. 战术导弹技术, 2012(2): 36-40. WANG Huan-xiang, LI Wei-min, SHANGGUAN Qiang, et al. Analysis of the battle demand to interception on the cruise phase of hypersonic vehicle[J]. Tactical Missile Technology, 2012(2):36-40.(in Chinese)
[5] 熊俊辉, 唐胜景, 郭杰. 基于空基拦截器的高超声速飞行器防御拦截[J]. 现代防御技术, 2014, 42(1): 14-18. XIONG Jun-hui, TANG Shen-jing, GUO Jie. Defense strategy of hypersonic vehicle based on air launched interceptor [J]. Modern Defense Technology, 2014, 42(1): 14-18. (in Chinese)
[6] 梁海燕. 反临近空间高超声速飞行器导引头及关键技术分析[J]. 飞航导弹, 2013(3): 61-63. LIANG Hai-yan. The key technology of seekers for anti-hypersonic vehicle in the near space[J]. Winged Missiles Journal, 2013(3): 61-63. (in Chinese)
[7] 赵杰, 王君, 张大元,等. 反临近空间高超声速飞行器中末交接视角研究[J]. 飞行力学, 2015, 33(3):253-256. ZHAO Jie, WANG Jun, ZHANG Da-yuan, et al. Visual angle research for midcourse and terminal guidance hand-over of near space hypersonic vehicles[J]. Flight Dynamics, 2015, 33(3):253-256. (in Chinese)
[8] 樊会涛. 复合制导空空导弹截获目标概率研究[J]. 航空学报, 2010, 31(6):1225-1229. FAN Hui-tao. Study on target acquisition probability of air-to-air missiles with combined guidance [J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6):1225-1229. (in Chinese)
[9] 李洪钶, 张斌, 赵雨. 采用双机协同的指令修正惯性中制导方法[J]. 空军工程大学学报:自然科学版, 2016, 17(1):13-18. LI Hong-ke, ZHANG Bin, ZHAO Yu. A study of method of command amendment inertial midcourse guidance based on dual aircraft cooperation[J]. Journal of Air Force Engineering University: Nature Science Edition, 2016, 17(1):13-18.(in Chinese)
[10] 姚郁, 郑天宇, 贺风华,等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报, 2015, 36(8):2696-2716. YAO Yu, ZHENG Tian-yu, HE Feng-hua, et al. Several hot issues and challenges in terminal guidance of flight vehicles [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8):2696-2716. (in Chinese)
[11] Ryu M Y, Lee C H, Tahk M J. Command shaping optimal guidance laws against high-speed incoming targets [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(10): 1-8.
[12] Dou L, Dou J. Design of optimal guidance laws with multi-constraints considering time-varying parameters[J]. Transactions of the Japan Society for Aeronautical & Space Sciences, 2013, 56(6):323-327.
[13] Padhi R, Kothari M. Model predictive static programming: a computationally efficient technique for suboptimal control design[J]. International Journal of Innovative Computing Information and Control, 2009, 5(2):399-411.
[14] Halbe O, Raja R G, Padhi R. Robust reentry guidance of a reusable launch vehicle using model predictive static programming[J]. Journal of Guidance Control & Dynamics, 2014, 37(1):134-148.
[15] Dwivedi P N, Bhattacharya A, Padhi R. Suboptimal midcourse guidance of interceptors for high-speed targets with alignment angle constraint[J]. Journal of Guidance Control & Dynamics, 2011, 34(3):860-877.
[16] Oza H B, Padhi R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J]. Journal of Guidance Control & Dynamics, 2012, 35(1):153-164.
[17] Newman B. Exoatmospheric intercepts using zero effort miss steering for midcourse guidance[C]∥Proceedings of AAS/AIAA Spaceflight Mechanics Meeting. Passadena, CA, US: AIAA, 1993: 415-433.
[18] Newman B. Spacecraft intercept guidance using zero effort miss steering, AIAA 93-3890[R]. Reston, VA, US: AIAA, 1993:1707-1716.
[19] 郑立伟, 荆武兴. 大气层外拦截器近最优中制导律设计[J]. 宇航学报, 2008, 29(1):235-241. ZHENG Li-wei, JING Wu-xing. Design of a near optimal midcourse guidance law for exoatmospheric interceptor [J]. Journal of Astronautics, 2008, 29(1):235-241. (in Chinese)
[20] Zarchan P. Tactical and strategic missile guidance [M]. 6th ed. Reston, VA, US: American Institute of Aeronautics & Astronautics, 1990.
Research on Command Correction Midcourse Guidance Law with Zero Effort Handover in Near Space
ZHANG Hao-qiang1, TANG Sheng-jing1, GUO Jie1, LIU Xiao1, XU Qian2
(1.Key Laboratory of Dynamic and Control of Flight Vehicle of the Ministry of Education, School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Beijing Institute of Aerospace System Engineering, Beijing 100076, China)
A space-based cruise phase defense strategy is proposed for near-space hypersonic vehicles. Considering the properties of near-space defense, a valid zero effort interception handover (ZEH) region and its performance criterions are presented by analyzing the handover region, which connects the midcourse and terminal guidance phases. Based on the model predictive static programming (MPSP) theory and the terminal constraints of midcourse phase, a close-formed solution is derived as the command correction guidance law. The proposed guidance law is used for simulation. The simulated results show that a small velocity-ratio condition for terminal engagement is satisfied by ZEH. The proposed method can improve the computational efficiency significantly, and also meet the requirement of ZEH constraint. A large number of Monte Carlo simulations show the robustness of the guidance law against initial disturbances.
ordnance science and technology; flight vehicle design; zero effort miss distance; handover point; model predictive static programming; midcourse guidance
2016-05-04
国家自然科学基金项目(11572036)
张浩强(1989—),男,博士研究生。E-mail:724158160@qq.com
唐胜景(1959—),男,教授,博士生导师。E-mail:tangsj@bit.edu.cn
TJ765.3+31
A
1000-1093(2017)03-0483-11
10.3969/j.issn.1000-1093.2017.03.010

