两级提拉式单侧弹射装置内弹道建模与优化
姚琳, 马大为, 马吴宁, 任杰, 仲健林, 王泽林
(南京理工大学 机械工程学院, 江苏 南京 210094)
两级提拉式单侧弹射装置内弹道建模与优化
姚琳, 马大为, 马吴宁, 任杰, 仲健林, 王泽林
(南京理工大学 机械工程学院, 江苏 南京 210094)
为延长导弹压缩空气弹射的有效推力行程,提出一种新型两级提拉式单侧冷弹射方案。采用Peng-Robinson真实气体方程,建立了弹射内弹道模型;在Simulink中搭建内弹道求解模块、在ADAMS中建立了冷弹射方案的虚拟样机,以气缸输出力、气缸位移和速度为状态变量,实现联合仿真,获得了内弹道参量的变化规律,并基于小型原理样机试验对仿真结果进行了验证。验证结果表明:第1级低压室压强先升后降;气缸换级过程中,低压室温度、压强与导弹加速度发生突变,但对导弹速度、位移影响较小。以气源容积最小为目标函数,选定约束条件和设计变量,应用遗传算法进行优化设计。优化后的气源容积降低了64.5%,优化结果大大提高了发射装置的机动性。研究结果验证了新型两级提拉式单侧冷弹射方案的可行性。
兵器科学与技术; 导弹冷弹射; 两级提拉式气缸; 单侧弹射装置; 真实气体效应; 优化设计
0 引言
当前,传统火药燃气冷弹射方式存在着发射阵地隐蔽性低、对热防护要求高、二次燃烧对内弹道影响较大、内弹道可控性差和成本昂贵等问题[1-2],新型压缩空气弹射技术能够较好地解决上述问题。压缩空气弹射的优点有:压缩气体瞬间膨胀性大、功率密度高[3-4];弹射压力变化平稳;工质温度低,无需热防护措施;内弹道简单可控;隐蔽无光,有利于提高生存能力、成本低廉等[5]。
目前,在导弹压缩气体弹射领域,已有学者开展了相关研究。白鹏英等[6]为了解决“在结构尺寸一定的情况下如何提高导弹离轨速度且最大过载不超过允许值”的问题,提出了2级3气缸同步提拉式弹射装置,建立了将两级弹射简化为单级弹射、且忽略多缸同步性问题的理想气体内弹道数学模型,对弹射过程的内弹道特性进行了分析。杨风波等[7]基于真实气体状态方程—维里状态方程,将对称式3级提拉弹射气缸简化为单级弹射气缸,建立了真实气体效应下的弹射内弹道模型,研究了弹射器在推弹过程中热力性质参数和内弹道的变化规律。Ren等[8]建立了压缩气体弹射过程中的压缩因子库,并以此为参考,建立了维里状态方程表示的高压气体余焓表达式。刘广等[9]利用多体动力学仿真软件ADAMS建立了单级低压室单侧弹射发射装置的虚拟样机,基于理想气体假设建立了内弹道模型并获得了气缸推力,对弹射试验的故障进行了复现。刘刚[10]研究了一种可以快速加压的单级气动灭火炮装置,建立了理想气体假设下的单级低压室击发内弹道模型。纵观已有文献,对气动弹射系统的研究多是基于单级气缸且多缸同步性良好假设开展的,而对于真实气体效应下考虑换级过程的两级提拉式气缸单侧弹射装置内弹道特性的研究鲜有报道。
本文提出一种新型两级提拉式单侧弹射方案:与气缸单级提拉式弹射器相比,在相同推弹行程下可以将弹射装置长度方向的尺寸减小1/4;与多缸多级提拉弹射装置相比,可以避免多个气缸的同步性问题。分别建立理想气体假设下和基于Peng-Robinson真实气体状态方程的两级提拉式弹射内弹道模型;在Matlab软件Simulink中搭建内弹道求解模块,在ADAMS中建立两级提拉式单侧弹射装置的虚拟样机,以气缸输出力、气缸位移和速度为状态变量,搭建基于Simulink/ADAMS的联合仿真模型,实现弹射过程的联合仿真,并通过缩比弹射试验验证仿真模型的正确性;为提高装置的机动性,基于遗传算法对弹射内弹道进行了优化设计。本文提出的两级提拉式单侧弹射装置和分析结果为弹射系统进一步的优化设计提供了参考。
1 两级提拉式单侧弹射装置虚拟样机
1.1 装置的结构组成
两级提拉式单侧弹射装置,其原理如图1所示。图2为第1、第2级低压室连通时的示意图。
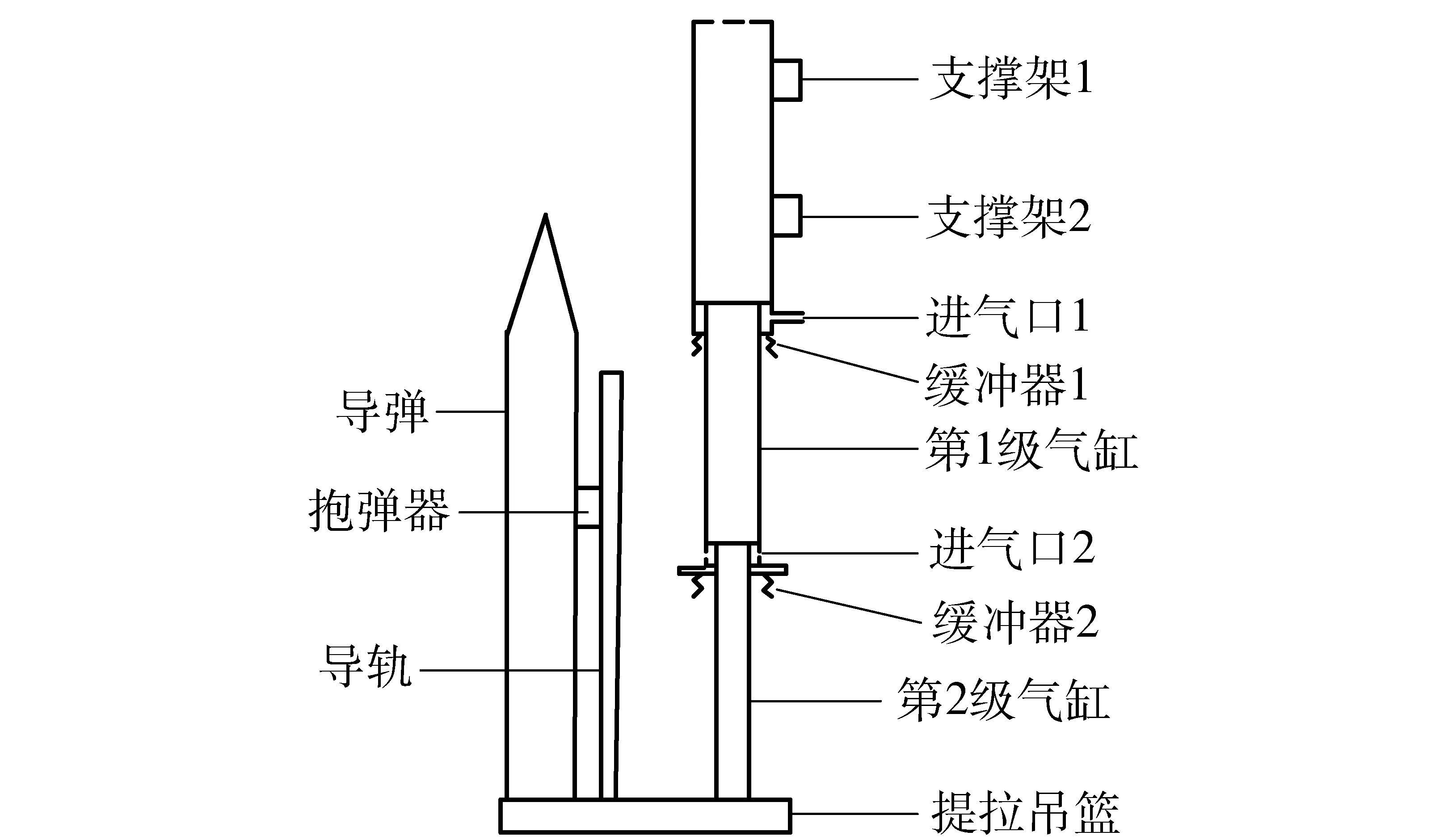
图1 两级提拉式单侧弹射装置原理图Fig.1 One-side ejection device with two-step cylinder
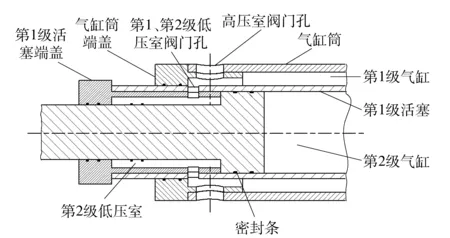
图2 两级低压室连通示意图Fig.2 Connection between two chambers
弹射装置主要由两级提拉气缸、支撑架、提拉吊篮、抱弹器、导轨和缓冲装置等部件组成。
1.2 工作原理
两级提拉弹射气缸的工作过程分为3个阶段:1)发射指令发出后,气动阀立即响应,高压气体从高压气瓶(高压室)进入第1级低压室,驱动第1级低压室加速运动,同时带动第2级低压室和导弹一起运动;2)第1级低压室达到设计行程后,进入缓冲过程,同时第1、第2级低压室阀门孔与一级低压室连通,高压气体进入第2级低压室,推动第2级低压室和导弹继续加速运动;3)当第2级低压室达到设计行程后,提拉吊篮撞击缓冲器,导弹离轨。
2 两级提拉弹射过程动力学模型
2.1 高压气动充放气过程基本假设
为简化问题,假设装置中所用高压空气为干空气;系统作用时间短,忽略传热过程;弹射过程中气体多变指数不变;阀门通流面积为线性增大;假设进气口2瞬时完全进入第1级低压室,即第1、第2级低压室间的通流面积瞬间等于进气口2的截面积;不考虑阀门处的结冰问题[11]。干空气的热物性参数如表1[11]所示。

表1 干空气的热物性参数Tab.1 Thermophysical parameters of dry air
2.2 考虑真实气体效应的内弹道模型
由文献[3]可知,相比于其他几种真实气体方程,Peng-Robinson方程具有较高精度。Peng-Robinson真实气体方程[12]:
(1)
式中:a、b为物质的固有常数;R为摩尔气体常数;T为气体温度。
将其应用到临界点,得
式中:Zc为气体临界压缩因子。
在临界温度以外的其他温度:
a(T)=a(Tc)α(Tr,ω),
(2)
式中:Tr为实际温度与临界温度的比值;ω为偏心因子;α(Tr,ω)为无量纲温度函数。
对大量物质的a与Tr的关系分析表明,二者关系符合线性方程:
(3)
式中:r为决定于物质种类的特性常数。经过拟合,得到了以偏心因子ω表达常数r的表达式为
r=0.374 64+1.542 26ω-0.269 92ω2.
(4)
经推导,得到基于Peng-Robinson真实气体状态方程的比热力学能u、比焓h表达式分别为
(5)
(6)
式中:Cvi为理想气体的比定容热容;v为比体积。
两级提拉弹射气缸内弹道按照第1.2节划分为两个阶段研究。内弹道模型共有10个自变量:ρH为高压室气体密度;TH、TL1、TL2分别为高压室和第1、第2级低压室气体温度;mL1、mL2分别为第1、第2级低压室气体质量;lL1为第1级低压室位移;vL1为第1级低压室速度;lL2为第2级低压室相对于第1级低压室位移;vL2为第2级低压室相对于第1级低压室速度;M为气体摩尔质量。
令X1=ρH,X2=TH,X3=mL1,X4=TL1,X5=lL1,X6=vL1,X7=mL2,X8=TL2,X9=lL2,X10=vL2. 根据高、低压室控制方程,得到基于Peng-Robinson真实气体状态方程的两级提拉弹射气缸第1阶段内弹道方程组。
第1阶段:
(7)
第2阶段:
(8)
(7)式和(8)式中:QmH为高压室流入第1级低压室的气体质量流量;VmH为高压室气体摩尔体积;VL10为第1级低压室初始体积;VmL1为第1级低压室气体摩尔体积;n为气缸数量;mm为导弹质量;QmL1为第1级低压室流入第2级低压室的气体质量流量;pH为高压室压强;pL1为第1级低压室压强;pL2为第2级低压室压强;VL20第2级低压室初始体积;VmL2为第2级低压室气体摩尔体积;VH为高压室体积;S1、S2为第1、2级气缸活塞推力面积;Cp为空气定压比热;m1、m2为第1、第2级气缸质量;f1、f2为第1、第2级气缸摩擦力;g为重力加速度;k1、c1为第1级气缸缓冲器的刚度与阻尼系数。
在弹射的第1阶段,第1级低压室由高压室补气,第2级低压室没有气体进入。高压室到第1级低压室的流量方程为
(9)
式中:AH、AL1分别为高压室到第1级低压室、第1级低压室到第2级低压室的等效通流面积;μx为流量修正系数;k为绝热系数;
在弹射的第2阶段,高压气体由高压室进入第1级低压室,然后第1级低压室的高压气体进入第2级低压室。从第1级低压室到第2级低压室的流量方程为
(10)
2.3 两级提拉弹射过程联合仿真模型建立
对弹射装置进行适当简化后,建立两级提拉式单侧弹射装置虚拟样机仿真模型,如图3所示。
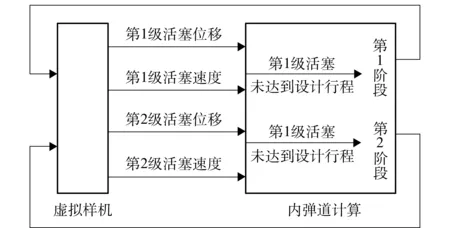
图3 联合仿真过程的数据交换原理图Fig.3 Schematic diagram of data exchange in co-simulation
将第1级低压室的位移、速度、推力,第2级低压室的位移、速度和推力设为状态变量,其中位移和速度变量作为ADAMS的输出变量,提供给Simulink内弹道求解模块;气缸推力为ADAMS的输入变量,由内弹道求解模块提供。仿真中的相关参数如表2所示,内弹道方程中10个变量的初始参数见表3.
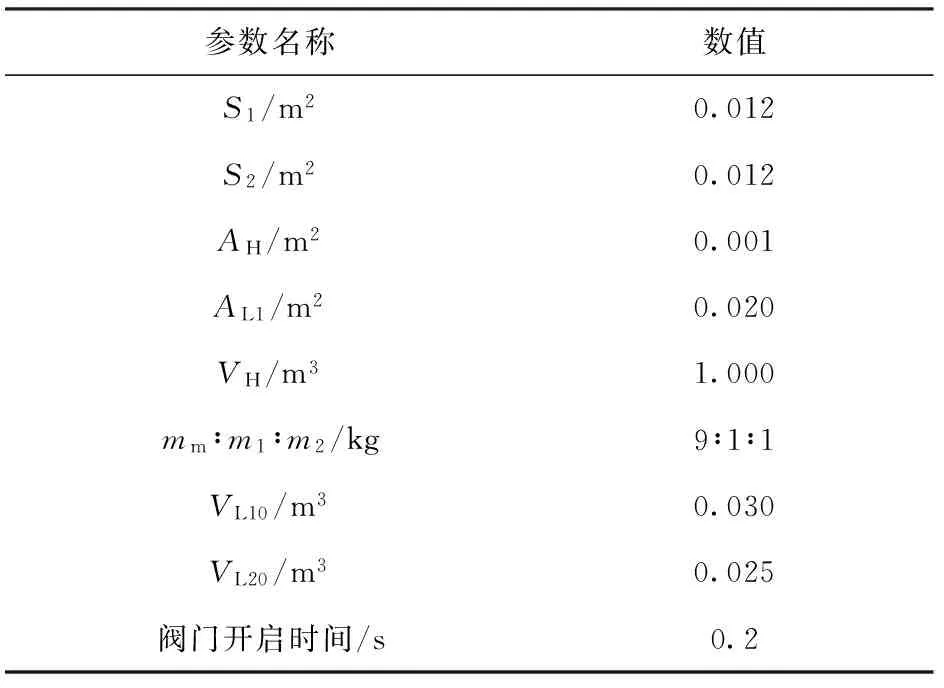
表2 模型中的相关参数Tab.2 Relevant parameters of model
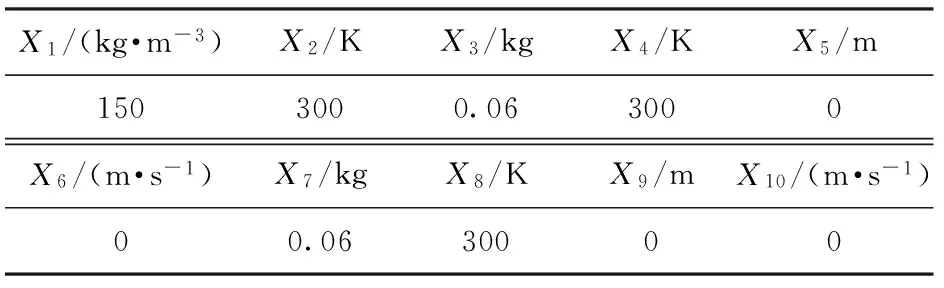
表3 各个变量的初始值Tab.3 Initial values of variables
2.4 联合仿真模型的试验验证
利用如图4所示的小型原理样机对弹射原理和联合仿真模型进行验证。

图4 试验装置示意图Fig.4 Schematic diagram of testing device
小型原理样机的气缸有效推力面积和提拉质量均为实际装置的1/10.
试验所选气瓶规格为15 MPa、50 L,环境温度为290 K,阀门响应时间为0.2 s. 压力传感器选用量程为20 MPa的Kistler传感器。压力传感器的工作原理为压电式,数据采集系统得到压力传感器输出的电信号后,乘以增益系数,即可得到气缸内压强。
限于试验条件,无法直接测得弹射物的速度变化曲线。试验采用加速度传感器设置于提拉吊篮的底部,直接测得弹射过程中的第2级气缸加速度信号,然后对信号进行积分,得到第2级气缸的速度变化曲线,即弹射物离轨前的速度变化曲线。
将试验装置的进气口1与高压气源管路连接,打开进气阀,在高压气体作用下,第1级活塞带动第2级活塞和提拉吊篮沿作动筒加速运动;当第1级活塞达到设计行程(1 m)后,第1级活塞的进气口2与第1级低压室连通,高压气体进入第2级低压室,推动第2级活塞继续运动;第2级活塞到达弹射行程后,阀门关闭,系统完成一次提拉试验。
将压强的试验测试结果与仿真结果进行对比,如图5所示。

图5 第1级低压室压强曲线Fig.5 Pressure curves of chamber
从图5中可以看出:第1级低压室内的压强计算结果与测量结果存在一定的误差,最大误差值为2.16 MPa,但最大误差百分比基本都小于10%. 此外,实际测得的气缸换级时刻要略滞后于仿真计算结果。
将弹射物速度的试验测试结果与仿真结果进行对比,如图6所示。从图6中可以看出,弹射物速度的计算结果与测量结果存在一定的误差:弹射前期,测试速度要大于仿真速度;弹射后期,测试速度要小于仿真速度。总体上,弹射物速度的最大误差小于10%,经过分析,误差是由于弹射过程中,进气口2瞬时打开的假设与实际情况有差别、气体压强的沿程损失、装置密封圈处存在泄漏、阀门开启过程的非线性、多处存在摩擦以及缸体与外界存在热交换等因素造成的。

图6 提拉吊篮速度曲线Fig.6 Acceleration curves
总体上看,通过仿真与试验得到的结果基本一致,这验证了弹射原理与联合仿真模型的合理性。
3 弹射过程内弹道响应分析与优化设计
3.1 弹射内弹道结果分析
图7~图8给出了导弹弹射过程中高、低压室的温度、压强变化曲线。图9给出了导弹运动学参数响应曲线。
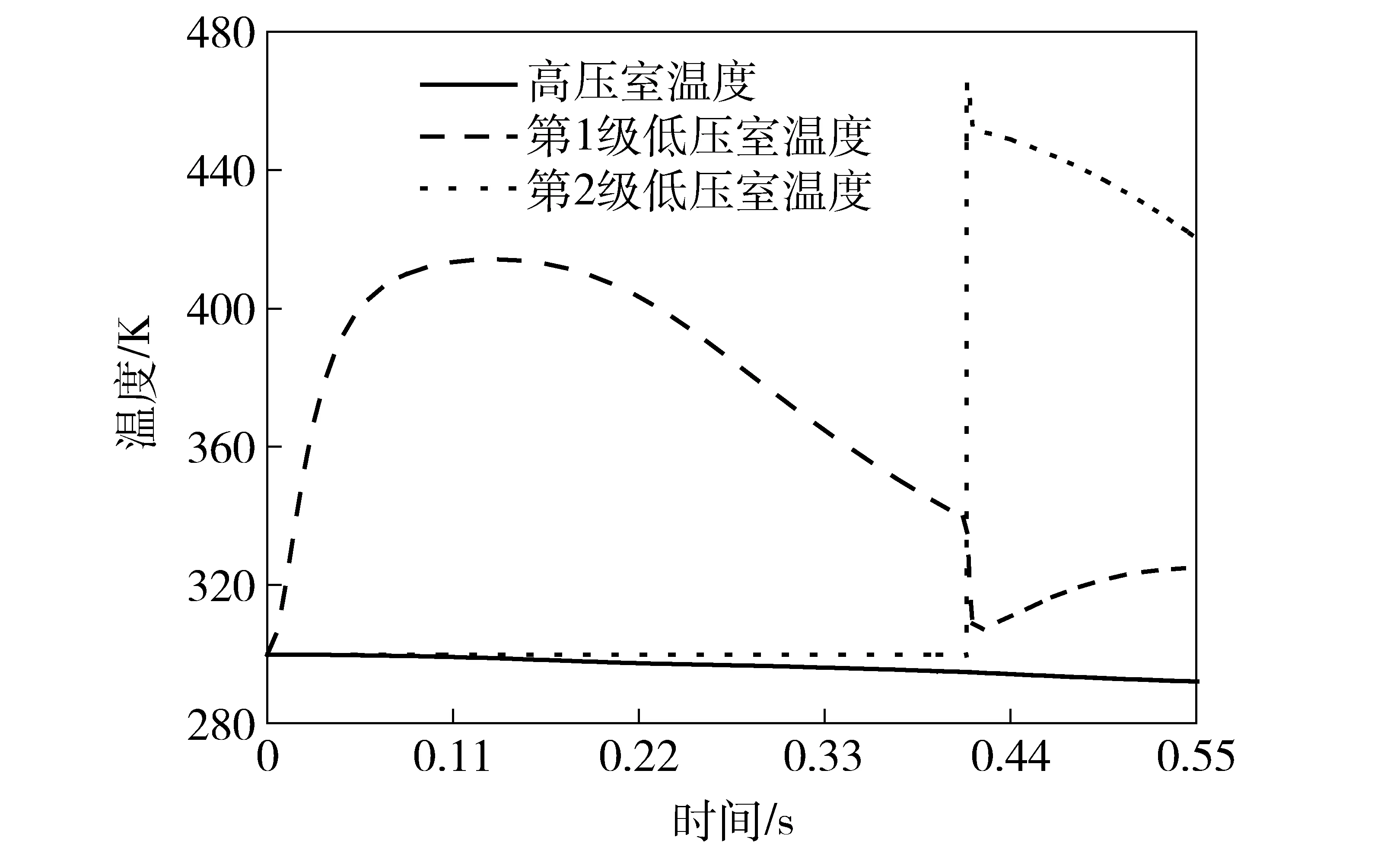
图7 温度曲线Fig.7 Temperature curves
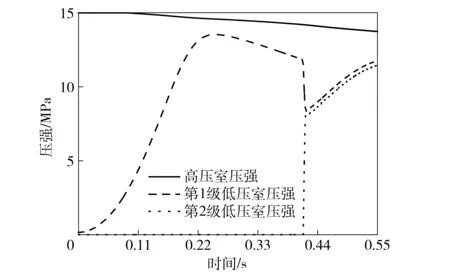
图8 各气室的压强曲线Fig.8 Pressure curves of chamber
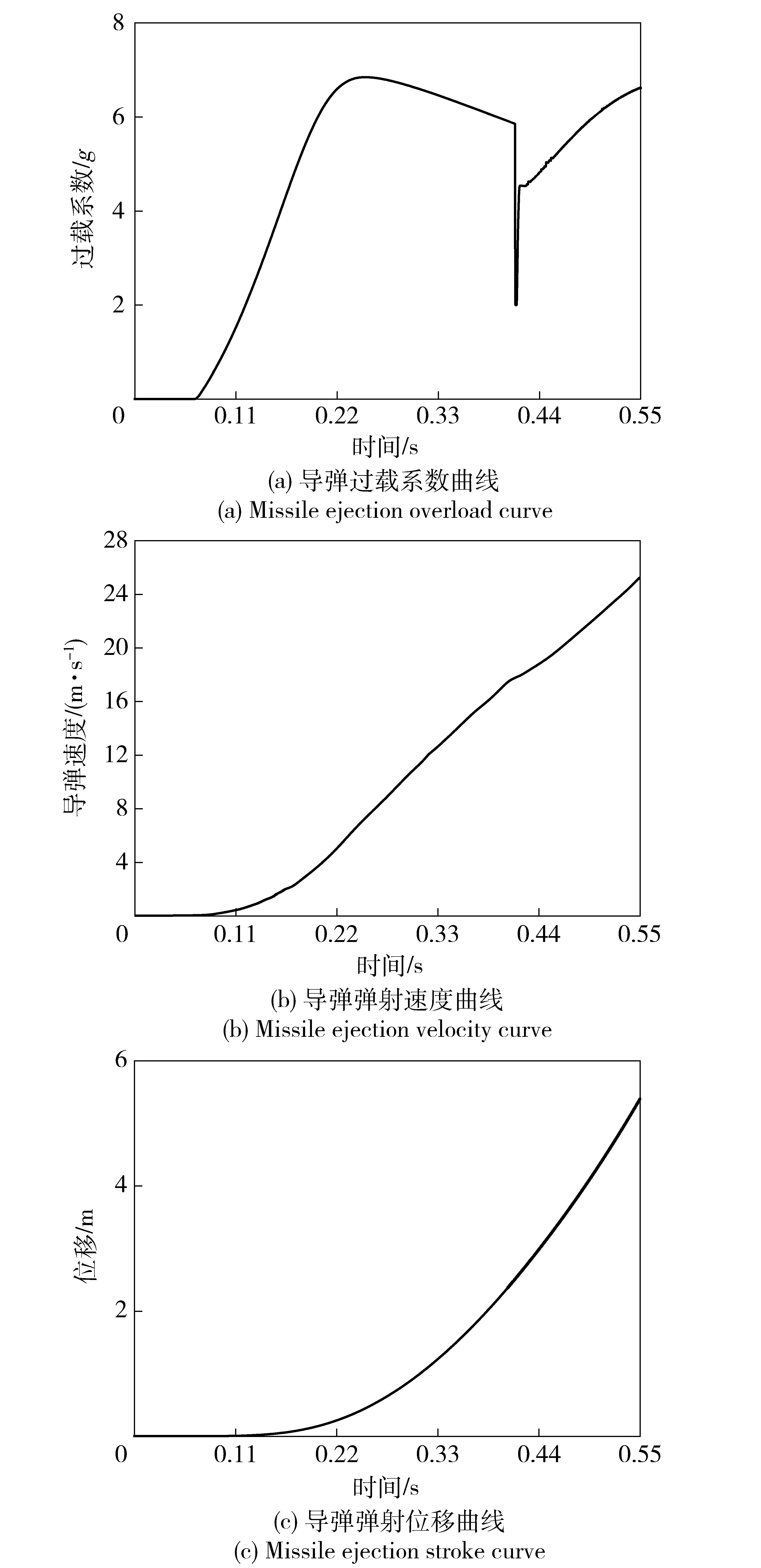
图9 导弹运动学参数变化曲线Fig.9 Missile kinematics parameter curves
由图7可知,随着弹射过程的进行,高压室不断对低压室进行充气,高压室温度逐渐降低,但降低的幅度不大。在弹射过程的第1阶段,第1级低压室温度先迅速升高又逐渐降低,这是因为初始阶段高压气体以较大的流量冲入第1级低压室,使低压室气体的能量迅速升高导致;随着导弹的加速运动,能量消耗逐渐加快且低压室体积逐渐增大,低压室温度呈现下降趋势。在气缸换级时,第1级低压室温度先出现剧烈降低,而后小幅升高的现象。这是因为气缸换级的初始阶段,第1级低压室气体迅速充入第2级低压室的初容室致使温度剧烈下降;随后出现的“小幅升高”现象,其原因与第1阶段出现该现象的原因一致。此外,气缸换级之后,第2级低压室的温度迅速升高后快速下降,原因与第1阶段出现该现象的原因一致,不再赘述。
由图8可知,高压室初始压强为15 MPa,高压室放气,压强不断降低。在第1阶段,第1级低压室不断充入高压气体,气缸内压强迅速升高,最高达到13.4 MPa左右;随着导弹的加速运动,第1级低压室体积加速增大导致压强出现下降。在气缸换级时,压强剧烈降低,之后小幅升高,这是由于气缸换级后,第1级低压室气体迅速进入第2级低压室的初容室所致,然后第1、第2级低压室压强接近相等,在高压室的继续充气下压强逐渐升高。
由图9可知,在0.4 s左右,两级提拉弹射气缸在换级时导弹过载系数由迅速降低后逐渐升高,原因是换级时第1级低压室所受合力会迅速降低,气体进入第2级低压室后第2级活塞推力会由0 N迅速增大;从导弹弹射速度和位移曲线可以看出,因为换级的时间很短,气缸换级过程对导弹的速度和位移变化的影响并不明显。
3.2 基于遗传算法的内弹道优化设计
为提高装置机动性,高压气源体积应越小越好[13]。选取高压气源体积为目标函数,以影响弹射性能的气缸有效推力面积、第1级和第2级低压室阀门孔的等效截面积、第1级初容室体积、第2级初容室体积4个参数作为设计变量。约束条件为:导弹最大过载系数不超过7g;导弹达到推弹行程(5 m)时的离轨速度不小于24 m/s.
基于遗传算法对内弹道进行优化设计。目标函数的收敛情况如图10所示。随着迭代次数的增加,震荡范围逐渐缩小;当迭代次数达到100次时,算法区域收敛。优化后,得到了高压气源体积的优化解为0.355 m3. 导弹的运动学参数如图11~图12所示。可以看出,过载系数小于7g,且导弹离轨速度满足不小于24 m/s的要求。相比于初始体积1 m3,优化后气源体积降低了64.5%,装置机动性得到明显提高。
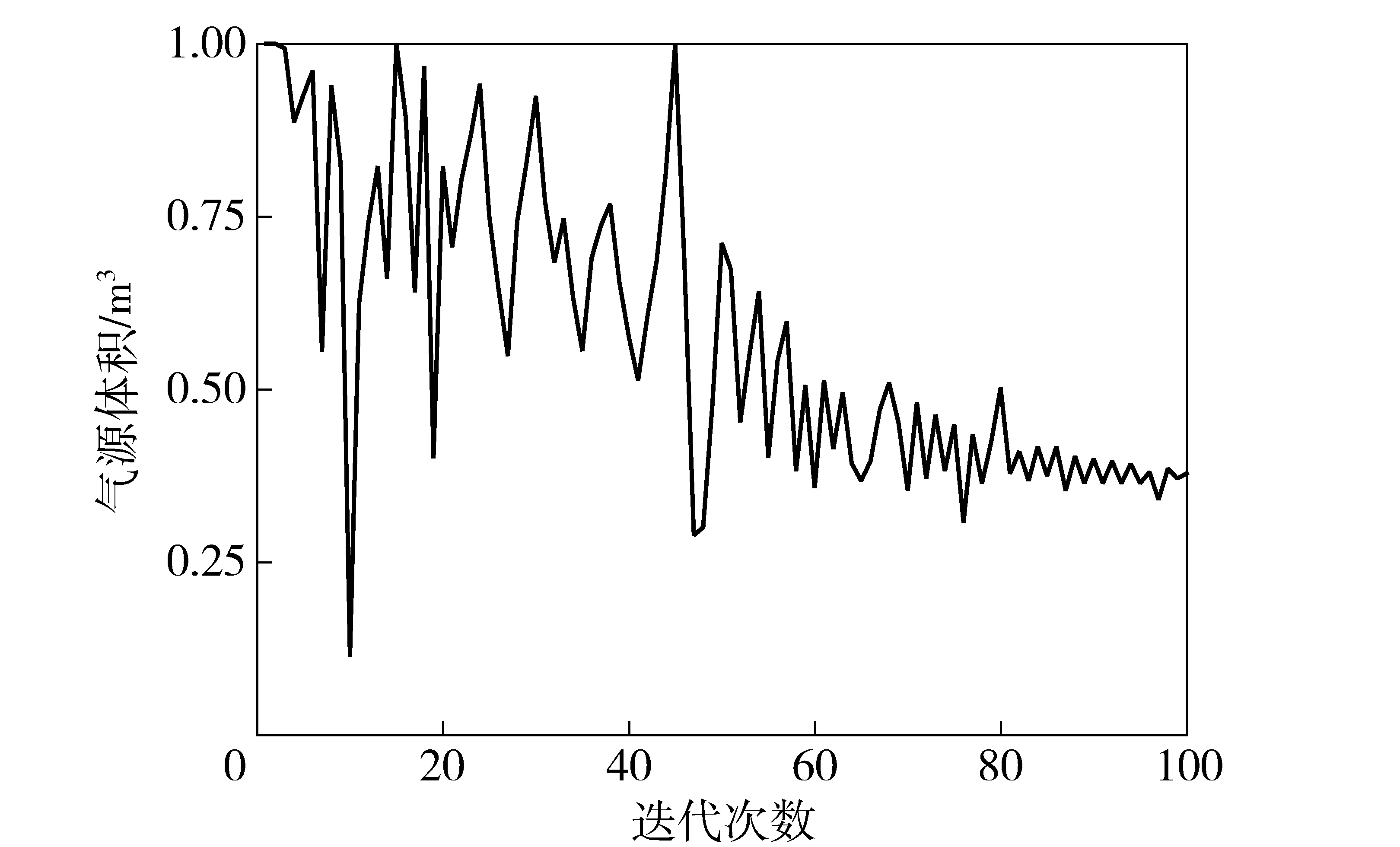
图10 收敛曲线Fig.10 Convergence curve
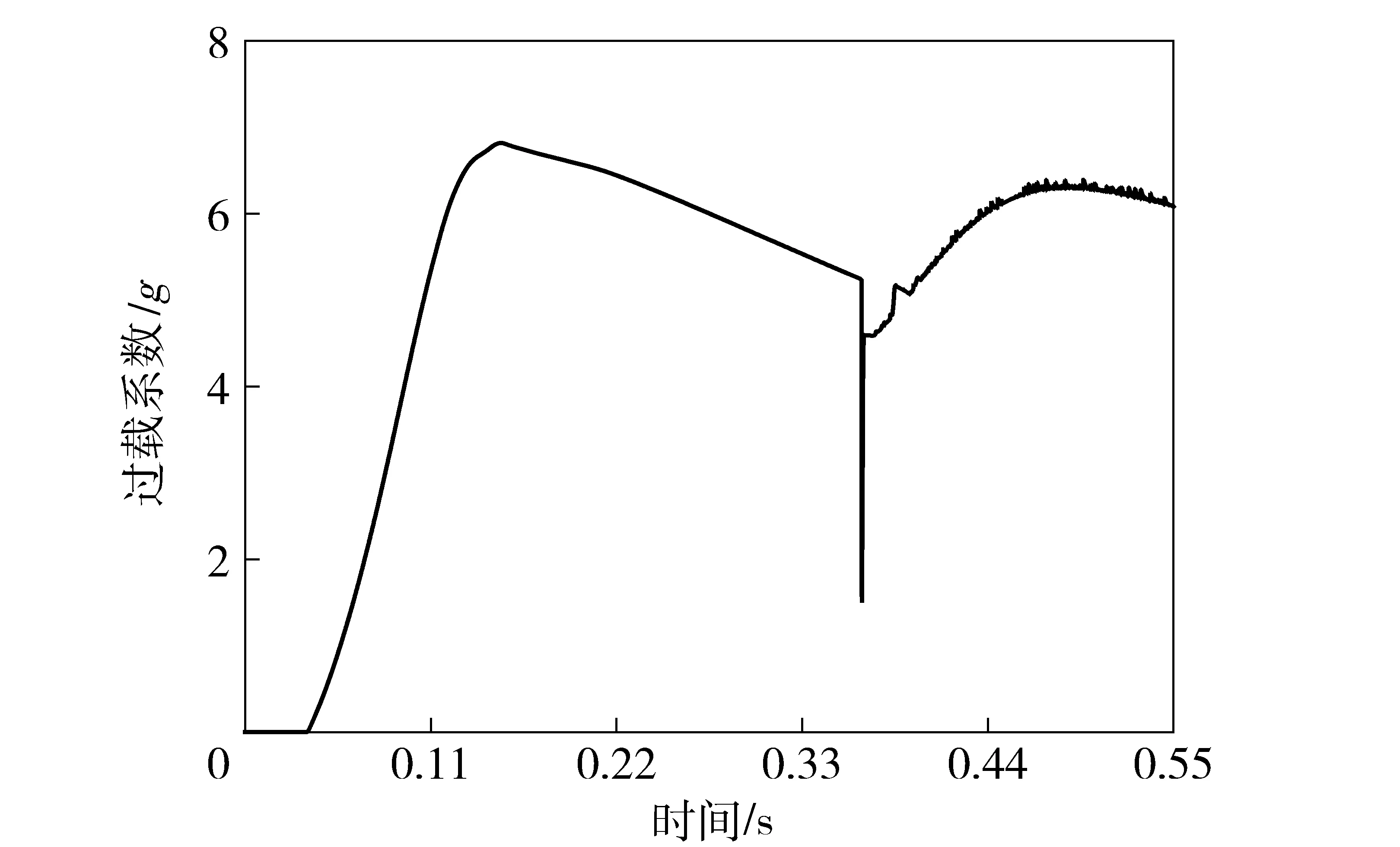
图11 导弹过载系数曲线Fig.11 Missile ejection overload curve
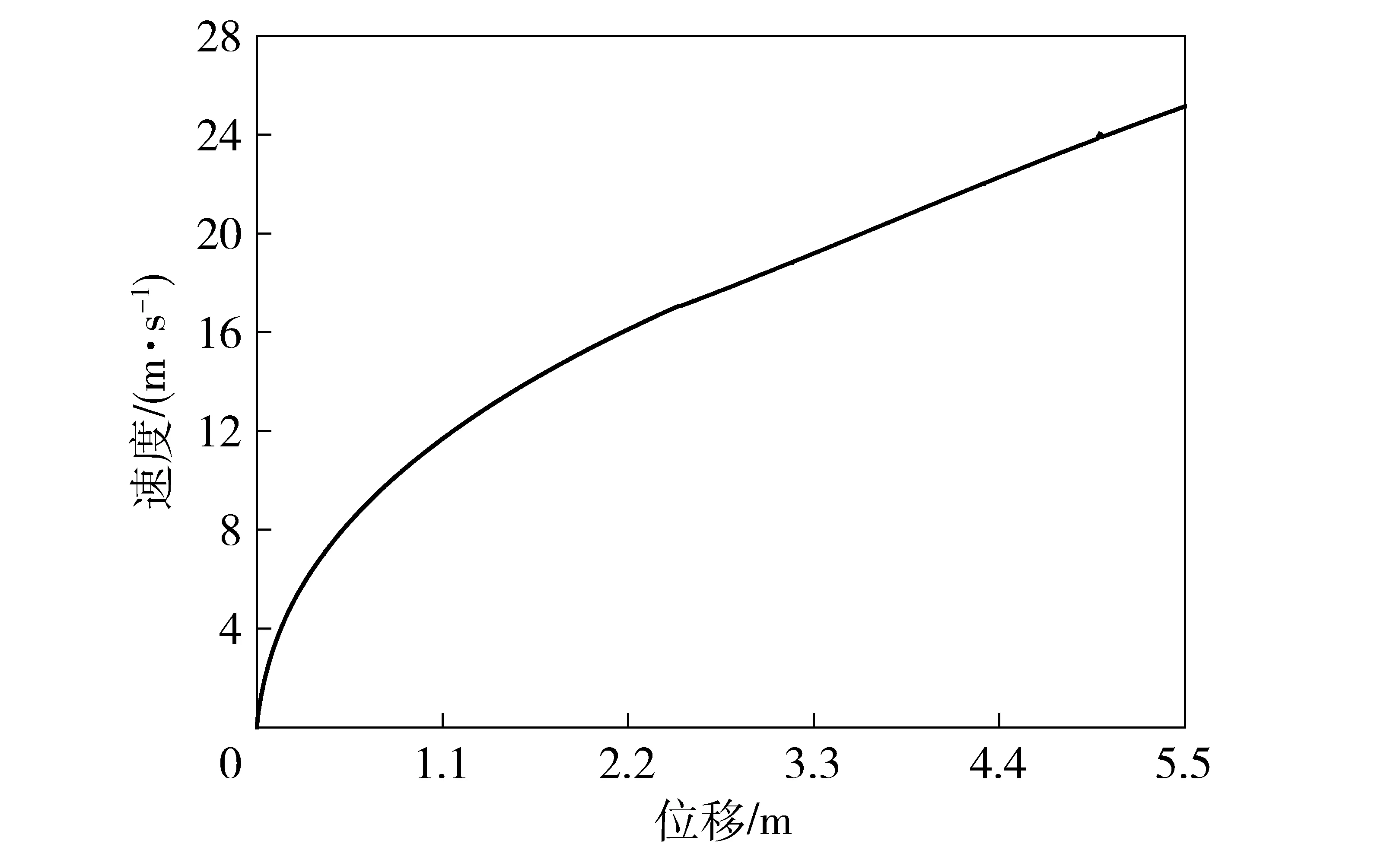
图12 导弹速度- 位移曲线Fig.12 Missile ejection velocity- stroke curve
4 结论
1)针对提出的一种两级气缸提拉式单侧弹射装置,构建了考虑高压气体真实气体效应的两级提拉弹射内弹道数学模型。
2)在ADAMS中建立了两级气缸提拉式单侧弹射装置的虚拟样机,在Simulink中搭建了内弹道方程组的求解模块。以气缸输出力、气缸位移和速度为状态变量,实现了弹射过程的联合仿真研究。并结合原理样机试验,对联合仿真结果进行了验证。
3)数值仿真结果表明:弹射过程中,第1级低压室压强先升后降;两级提拉式气缸换级过程中,低压室的温度、压强与导弹加速度会发生突变,但对导弹速度和位移的影响较小。
4)为了提高装置的机动性,基于遗传算法对弹射内弹道进行了优化设计。优化结果显示气源体积降低了64.5%,装置机动性得到明显提高。
References)
[1] 胡晓磊,乐贵高,马大为,等. 环形腔对燃气弹射初容室二次燃烧影响数值研究[J]. 兵工学报,2015,36(6):1024~1032. HU Xiao-lei, LE Gui-gao, MA Da-wei, et al. The influence of annular cavity on secondary combustion of gas-ejection initial cavity[J]. Acta Armamentarii, 2015, 36(6):1024-1032. (in Chinese)
[2] 李仁凤, 乐贵高, 马大为. 燃烧产物特性对燃气弹射内弹道与载荷的影响研究[J]. 兵工学报, 2016, 37(2):245-252. LI Ren-feng, LE Gui-gao, MA Da-wei. The influence of combustion product properties on gas-ejection interior ballistic and load characteristics[J]. Acta Armamentarii, 2016, 37(2):245-252.(in Chinese)
[3] Luo Y X, Wang X Y. Exergy analysis on throttle reduction efficiency based on real gas equations[J]. Energy, 2010, 35(1):181-187.
[4] 卢伟, 马晓平, 周明, 等. 无人机气动弹射动力学仿真与优化[J]. 西北工业大学学报, 2014, 32(6):866-871. LU Wei, MA Xiao-ping, ZHOU Ming, et al. Dynamic simulation and optimization of UAV pneumatic launching[J]. Journal of Northwestern Polytechnical University, 2014, 32(6):866-871.(in Chinese)
[5] 杨风波, 马大为, 杨帆, 等. 高压弹射装置内弹道建模与计算[J]. 兵工学报, 2013, 34(5):527-534. YANG Feng-bo, MA Da-wei, YANG Fan, et al. Interior ballistics modeling and calculation of high-pressure ejection device[J]. Acta Armamentarii, 2013, 34(5):527-534.(in Chinese)
[6] 白鹏英, 乔军, 方向. 双级气缸式弹射装置内弹道分析[J]. 现代防御技术, 2007, 35(4):44-49. BAI Peng-ying, QIAO Jun, FANG Xiang. Analysis about the interior trajectory of two-step cylinder ejection device[J].Modern Defence Technology,2007, 35(4):44-49. (in Chinese)
[7] 杨风波, 马大为, 朱忠领, 等. 基于真实热力学过程分析的气动弹射性能研究[J]. 机械工程学报, 2013, 49(24):167-174. YANG Feng-bo, MA Da-wei, ZHU Zhong-ling, et al. Pneumatic catapult performance research based on the true thermo dynamic process analysis[J]. Journal of Mechanical Engineering, 2013, 49(24):167-174.(in Chinese)
[8] Ren J, Yang F B, Ma D W, et al. Pneumatic performance study of a high pressure ejection device based on real specific energy and specific enthalpy[J]. Energy, 2014, 16(9):4801-4817.
[9] 刘广, 许斌, 杨积东. 单侧弹射发射系统故障虚拟复现与设计改进[J]. 系统仿真学报, 2013, 25(7):1683-1691. LIU Guang, XU Bin, YANG Ji-dong. Virtual replay of failure and design modification of one-side ejection launching system[J]. Journal of System Simulation, 2013, 25(7):1683-1691.(in Chinese)
[10] 刘刚. 气动发射式高层建筑灭火炮研究[D]. 哈尔滨:哈尔滨工程大学, 2012. LIU Gang. Research on pneumatic fire-extinguish cannon for high-rise building[D]. Harbin:Harbin Engineering University, 2012. (in Chinese)
[11] 徐志鹏, 王宣银, 罗语溪. 滑阀先导式高压气动减压阀结冰特性[J]. 航空学报, 2009, 30(5):819-824. XU Zhi-peng, WANG Xuan-yin, LUO Yu-xi. Characteristics of icing in high pressure pneumatic relief valve with slide pilot[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(5):819-824.(in Chinese)
[12] 刘娟芳, 刘朝. 高温高压下湿空气的焓和熵计算[J]. 工程热物理学报, 2007, 28(4):557-560. LIU Juan-fang, LIU Chao.The calculations of moist air’s enthalpy and entropy in high temperature and pressure[J].Journal of Engineering Thermophysics, 2007, 28(4):557-560.(in Chinese)
[13] 陈则韶. 高等工程热力学[M]. 北京:高等教育出版社, 2008. CHEN Ze-shao. Advanced engineering thermodynamic[M]. Beijing: Higher Education Press, 2008.(in Chinese)
Interior Ballistics Modeling and Optimization of One-side Ejection Device with Two-step Cylinder
YAO Lin, MA Da-wei, MA Wu-ning, REN Jie, ZHONG Jian-lin, WANG Ze-lin
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)
A kind of one-side ejection device with two-step cylinder is proposed to increase the effective thrust travel of missile pneumatic launching system. The real gas state equation, Peng-Robinson equation, is used as theoretical basis. The mathematical expressions of pneumatic interior ballistics model are deduced on the basis of 'P-R' state equation for the two-step cylinder. The interior ballistics equation is solved by using Simulink software, and the one-side launching ejection is built by means of ADAMS. The co-simulation model of device is achieved. The results show that the pressure of first-order lower-chamber rises first and then falls. It can be seen from the calculated result that both the thermodynamic parameters and the missile acceleration obviously fluctuate in the process of cylinder changing, but their influences on missile speed and displacement are very small. To reduce the equipment volume, the air source volume is selected as the objective function. The air source volume optimized by genetic algorithm is decreased by 64.5%, thus improving greatly the mobility of launcher.
ordnance science and technology; missile cold launching; two-step cylinder; one-side ejection device; real gas effect; optimal design
2016-04-20
国家国防科技工业局技术基础科研项目(B2620116005);江苏省普通高校研究生科研创新(实践)计划项目(KYLX15_0328)
姚琳(1988—),男,博士研究生。E-mail:yaolinxueshu@163.com
马大为(1953—),男,教授,博士生导师。E-mail:ma-dawei@mail.njust.edu.cn
TJ768.2+8
A
1000-1093(2017)03-0466-10
10.3969/j.issn.1000-1093.2017.03.008

