机器人航天员冗余机械臂自运动优化

刘世平，赫向阳，，韩亮亮，李世其，付 艳

（1.华中科技大学机械科学与工程学院，武汉430074；2.上海宇航系统工程研究所，上海201108）

·工程技术·

机器人航天员冗余机械臂自运动优化

刘世平1，赫向阳1，2，韩亮亮2，李世其1，付 艳1

（1.华中科技大学机械科学与工程学院，武汉430074；2.上海宇航系统工程研究所，上海201108）

为增强机器人航天员的工作能力，机器人航天员的手臂采用七自由度仿人机械臂。根据S⁃R⁃S构型七自由度冗余手臂的结构特性，采用臂型角参数化的方法求解运动学。该方法将冗余机械臂的自运动用臂型角来描述，通过对臂型角的二次优化来限制机械臂的自运动。为了使仿人臂处于一种自然的构型和姿态，定义了“偏离中心度”的指标来表示关节偏离中心位置的程度，通过这个评价指标来描述仿人臂的最优位形，从而建立自运动优化函数。采用具有线性减小惯性权重的粒子群优化算法来寻找自运动优化函数的最优解。最后在机器人航天员平台进行验证，可以快速有效地完成冗余手臂自运动优化。

冗余机械臂；运动学；自运动优化；粒子群算法

1 引言

随着机器人技术的发展，机器人在空间的应用彰显了巨大的潜力［1］，尤其是具有高灵活性和运动协调性的类人机器人，可以辅助人类宇航员完成空间站内外的设备维护和科学实验，降低出舱风险。针对机器人航天员在空间站和星体探索中的工作任务特点，本文设计了双臂冗余手臂机器人。冗余机械臂由于机械臂的自由度数目大于末端位姿参数数目，关节空间存在着无数组解与目标末端位姿对应。采用冗余结构的机械臂相比于常见的六自由度机械臂，有着许多不可替代的优点，在增强机械臂在执行任务的可靠性、实用性［2］的同时，还可以实现避障［3］、容错［4］和关节力矩优化［5］等功能。NASA和通用汽车公司联合研发的新一代灵巧机器人Robonaut 2［6］以及德国航空航天中心研制的仿人双臂机器人 Rollin’Justin［7］都是采用了七自由度冗余机械臂。

冗余机械臂的自运动是指在末端位姿确定的情况下，机械臂关节空间存在无数组连续的解与目标末端位姿相对应，这些关节空间解的集合形成冗余机械臂的自运动流形［8］。冗余机械臂相对于非冗余机械臂的优点，都是通过自运动表现出来的，所以自运动的优化有很重要的意义。

目前冗余机械臂的自运动优化问题，通常通过微分运动学法或者数值方法来求解。张雨浓等［9］通过微分运动学法，考虑关节位置极限和速度极限，对PA10机械臂进行了自运动规划。任子武等［10］通过智能迭代算法，构建冗余关节角的最优组合来求解机械臂的逆运动学。这些方法有一定的局限性，基于微分运动学的规划并不能求得逆运动学的全部可行解，智能迭代算法，需要大量的运算去逼近目标值，在保证计算精度的同时难以获得求解的快速性。

本文建立了基于臂形角的七自由度运动学求解方法，并通过臂形角来描述冗余机械臂的自运动，采用最优位形来优化机械臂的自运动，实现冗余机械臂运动过程中机械臂自运动的优化，保证了计算过程的精确度和快速性。

2 臂形角参数化运动学

2.1冗余机械臂正运动学

仿人机械臂采用串联球形关节⁃旋转关节⁃球形关节的形式（简称S⁃R⁃S），前三个关节互相垂直相交于一点，形成球铰对应人体的肩关节，同理后三个关节垂直相交于一点，形成腕关节，中间的旋转关节称之为肘关节。这种构型能够最大程度的模拟人体的手臂，根据这种构型设计了仿人机械臂，如图1所示。为了增加机械臂的运动范围，肘关节设计有一定的位置偏置。

为了求解机械臂的运动学，建立机械臂的DH坐标系，其中坐标系｛0｝为基坐标系，与连杆i固接的坐标系记为坐标系｛i｝，如图2所示。同时建立DH参数表，其中，ai为连杆长度，αi为连杆扭角，di为相邻连杆距离，θi为两连杆的夹角，如表1所示。

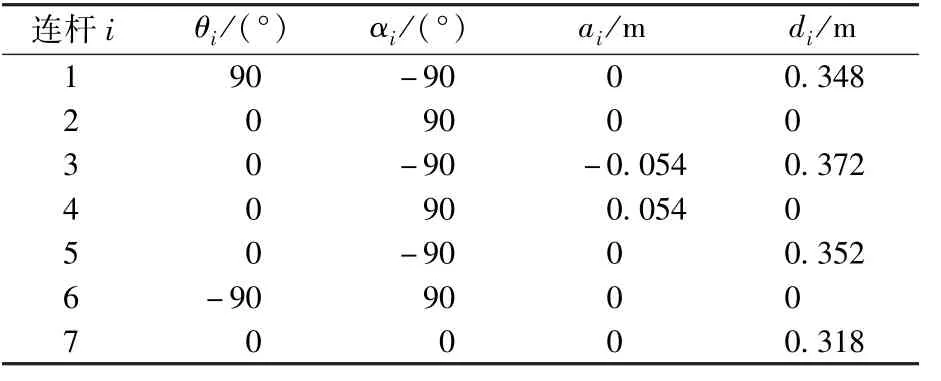
表1 七自由度机械臂DH参数Table 1 DH parameters of the 7⁃DOF manipulator

根据D⁃H参数表，可以得到相邻坐标系的齐次变换矩阵如式（1）所示：

将相邻坐标系的齐次变换矩阵依次连乘，可以得到机械臂末端坐标系相对于基座的变换矩阵0T7，即机械臂运动学正解的通式：

2.2冗余机械臂逆运动学

冗余机械臂在工作过程中的一种姿态可以用图3表示，其中基座、肩关节、肘关节、腕关节和末端分别记为B、S、E、W和T。从当前的姿态可以发现，肩关节、肘关节和腕关节可以构成一个平面，定义这个平面为臂平面。在已知末端位置0T7时，S点、W点以及向量SW的值是唯一的。冗余机械臂的自运动表现为：肩关节、肘关节和腕关节构成的平面绕SW旋转运动。本文定义关节1轴线的方向BS与肩关节和腕关节方向SW形成的平面为参考平面。臂平面与参考平面生成的夹角，定义为臂型角，记作ψ。这样，冗余机械臂的自运动可以通过臂形角完整地描述。

已知机械臂末端位姿0P7和0R7，向量SW可以表示为：

机械臂自运动不会影响肘关节大小，所以θ4与臂型角ψ无关：

在基坐标系中，臂平面相对于参考平面的旋转矩阵为：

式中：I3为3×3的单位阵，SW∗为向量SW的叉乘因子。

当三号坐标系在参考平面内时，三号坐标系与基座坐标系之间的关系用来表示，0x3，0y3和0z3表示三号坐标系的方向向量。

由于肘关节偏置的存在，0y3相对于基坐标系的角度γ由两部分组成：转动形成的角度α和偏置产生的角度 β，存在公式（6）～（8）所示的关系：

0y3相对于基坐标系的旋转矩阵为：

根据公式（10）、（11）可得：

则三号坐标系相对于基坐标系的姿态可以表示为：

根据正运动学方程（1）可得0R3：

式中：si＝ sinθi，ci＝ cosθi。

方程（13）（14）对应项相等，即可求出关节角θ1、θ2和 θ3。

同理，坐标系4相对于坐标系7可以表示为：

方程（15）（16）对应项相等，即可求出关节角θ5、θ6和 θ7。

至此，可以得到机械臂臂型角参数化的运动学逆解。根据已知的机械臂末端位置和臂型角ψ的值，按照本文提出的运动学求解方法，可以准确地得到关节位置的8组解，通过合理的二次规划可以实现冗余机械臂自运动控制。

3 机械臂自运动优化

经过臂形角参数化的机械臂，其自运动可以通过臂形角来描述。对于给定的机械臂末端位置，只要确定机械臂的自运动就可以确定机械臂各关节的角度值。为了使运动学求解的结果满足人形机械臂处于自然位姿的要求，同时也为后续机械臂的轨迹规划和避障提供足够的运动空间，机械臂的最优位形定义为最大程度地靠近关节的中心位置，为关节运动提供最大的活动裕量。

粒子群算法（Particle Swarm Optimization，PSO）是一种智能优化算法［11］。PSO类似于遗传算法，通过迭代的方式进行优化寻值。粒子初始化为一群随机粒子，在每一次迭代中通过跟踪粒子本身历史的最优位置和群体的最优位置，在一定随机扰动的情况下决定下一步的搜索方向。在迭代过程中，粒子的位置目标函数都被评估。

受关节限位的约束，根据实际机械臂的构型，各关节可到达的关节运动范围如表2所示。

表2 机械臂关节运动范围Table 2 Range of the joint angles

机械臂自运动的优化，转化为对“偏离中心度”指标μ的优化。根据关节“偏离中心度”指标最小化要求，确定机械臂的最优位形，定义PSO适应度函数如式（18）：

式中，μ（i）max表示七个关节中关节“偏离中心度”指标μ最大的值。适应度函数的值越小，表示七个关节中最大的“偏离中心度”指标越小，获得的机械臂自运动优化越好。适应度函数的自变量ψ就是所求的最优臂型角。

为了提高算法性能，采用引入惯性权重w的PSO。惯性权重w决定了粒子先前速度对当前速度的影响程度，惯性权重w大，全局探索能力强，惯性权重w小，局部搜索能力强。Y.Shi和R. Eberhart［13］提出了线性减小惯性权重w的自适应策略，惯性权重w表示为式（19）：

式中：wmax为最大权重系数，wmin为最小权重系数，tmax为最大进化次数。

这样，速度更新方程表示为式（20）：

式中：c1和c2表示粒子自我总结和学习的能力，通常范围在［1，2］之间的寻优效果最好；rand（）是［0，1］之间的随机数；粒子的移动速度被限制在［－Vmax，Vmax］之间；pij是粒子历史最优位置，pgj是群体全局最优位置。粒子群算法的流程如图4所示。

4 运动仿真与试验验证

为了验证上述冗余机械臂运动学的求解和自运动优化效果，以仿人七自由度机械臂为平台，通过数值计算和实物来验证算法的有效性。

4.1参数化运动学求解

在冗余机械臂的工作空间内，选择任意的一个末端位置，位置0P7＝［－0.6，0.3，0.8］，0R7＝［0，－90，0］（采用ZXZ旋转欧拉角）。在不考虑关节限位的情况下，选择一个任意位置的臂型角ψ＝－160°，对机械臂的运动学求解。逆运动学解可以获得8组解，如表3所示。根据运动学方程（2）对8组关节角求正运动学解，然后进行欧拉角的转换得到实际末端位姿，与期望位姿进行比较，误差在10－14m左右，由此可以验证参数化运动学算法的精确性。对于固定臂型角时逆运动学8组解的选取，采用偏离中心度最小的方法。对8组解分别求偏离中心度值，最优解是第三组解。

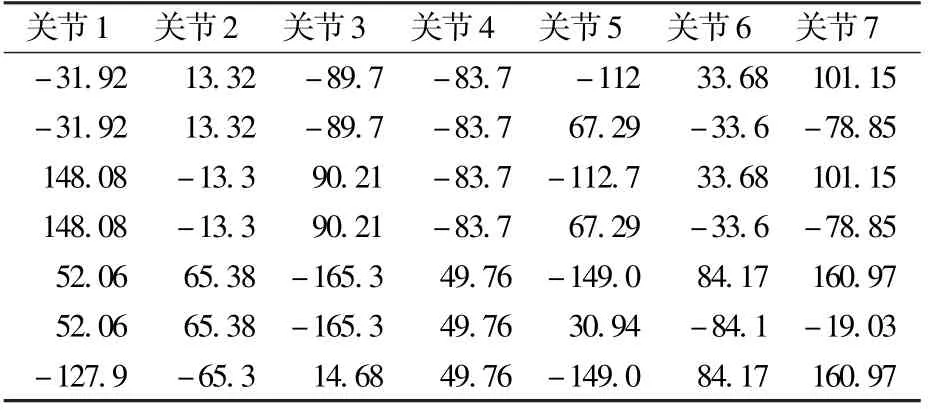
表3 机械臂逆运动学解Table 3 Results of inverse kinematics

4.2自运动优化验证

在参数化运动学求解验证过程中，臂型角ψ通过人为来设定。在考虑机械臂自运动优化的条件下，利用文中提出的PSO优化算法，对机械臂的自运动进行优化。求解过程中，粒子群算法的参数设置如下：搜寻空间臂形角ψ∈［－π，π］，种群规模N＝50，迭代次数为50，c1＝2，c2＝2，粒子速度更新式中的惯性权系数wmax＝1，wmin＝0．8，速度限定vmax＝1，vmin＝－1。

通过计算，可以得到臂型角ψ的最优值，ψopt＝175．97°，适应度值最小为0.305，计算时间为8 ms。绘制适应度值与进化代数曲线，如图5所示。通过曲线可以看到进化20代以后，适应度已经非常接近最优值。

此时，最优自运动条件下的运动学解为当前臂型角的第 3组解：q ＝［－81.069 －3.172－58.72 －83.73－91.21－49.69－96.06］。在MATLAB机械建模与仿真环境（Sim Mechanics）中进行仿真，分别输入优化前和优化后关节位置，得到机械臂实际的关节位置如图6所示。

与不考虑自运动优化，ψ＝－160°的第3组解比较，得到两种情况下各关节“偏离中心度”μ的值，优化前 μinit＝［0.740 0.111 0.289 0.014 0.415 0.140 0.334］，优化后μopt＝［0.681 0.2880.106 0.014 0.272 0.305 0.301］，如图7所示。

通过比较可以发现，关节4优化后与优化前效果相同，这是由于基于臂形角的自运动优化对肘关节没有作用。优化后比优化前的关节“偏离中心度”值更小，即关节的活动裕量更大，机械臂的位形更符合人体关节构型，自运动优化达到了期望的效果。

4.3轨迹跟踪优化验证

在验证固定点位置的自运动优化后，为保证算法的适用性，进行轨迹跟踪优化验证。只考虑关节末端的位置变化，不考虑末端姿态变化，定义机械臂期望轨迹为：

设置最小步长Δt＝0.1 s，利用提出的自运动优化算法进行轨迹跟踪。在仿真模型里，可以得到机械臂在笛卡尔空间的轨迹跟踪结果，如图8所示。通过笛卡尔空间的轨迹可以看出，跟踪轨迹的点基本都落在期望轨迹上，表明自运动优化方法在轨迹跟踪中普遍适用。

同时，可以得到轨迹跟踪的误差，如图9所示。得到的误差精度在10－15m范围内，表明算法具有很高的精确性。

在仿真周期内对最优臂型角和粒子群算法的适应度值进行记录，得到的结果如图10所示。最优臂型角和PSO适应度连续变化，没有出现突变。PSO适应度值最大为0.52，表明距离关节限位最近的距离还有很大的运动裕量，满足最优位形的要求。

在仿真周期内对各关节角度变化进行记录，得到的结果如图11所示。曲线表明，在一个周期内关节角度连续变化，没有突变。每条曲线左右两端点角度值相等，表明整个过程连续并且可以循环。

在机器人航天员平台上进行验证，采用与仿真模型相同的运动轨迹，运动过程中机械臂响应快速稳定，运动过程如图12所示。图（a）、（b）、（c）、（d）分别表示在时间2／5π、4／5π、6／5π和8／5π时的位姿。

5 结论

本文根据S⁃R⁃S形式的冗余机械臂结构特性，采用臂型角的方法对机械臂进行关节的参数化，并通过臂型角对机械臂的自运动进行优化。这种参数化的封闭解能够获取所有的可行解，同时保证了计算精度。采用具有线形减小惯性权重的PSO算法，避免了陷入局部最优解，同时提高了搜寻速度。通过在机器人航天员平台的验证，表明提出的自运动优化算法具有保持机械臂最优位形的作用。

这种方法对机械臂的构型有特殊要求，但这种构型普遍应用在仿人机械臂中，具有广泛的适用性。基于最优位形的自运动优化可以使机械臂快速、平稳地到达目标位姿，如果要实现避障等功能，可以通过在最优位形的基础上对机械臂进行二次规划来实现。

（References）

［1］ Diftler M A，Culbert C J，Ambrose R O，et al.Evolution of the NASA／DARPA robonaut control system［C］／／Robotics and Automation，2003.Proceedings.ICRA＇03.IEEE Inter⁃national Conference on.IEEE，2003，2：2543⁃2548.

［2］ Zanganeh K E，Angeles J.Mobility and position analyses of a novel redundant parallel manipulator［C］／／Robotics and Au⁃tomation，1994.Proceedings.，1994 IEEE International Con⁃ference on.IEEE，1994：3049⁃3054.

［3］ Lee K K，Komoguchi Y，Buss M.Multiple obstacles avoid⁃ance for kinematically redundant manipulators using Jacobian transpose method［C］ ／／SICE，2007 Annual Conference. IEEE，2007：1070⁃1076.

［4］ Assal S F M，Watanabe K，Izumi K.Neural network⁃based kine⁃matic inversion of industrial redundant robots using cooperative fuzzy hint for the joint limits avoidance［J］.Mechatronics，IEEE／ASME Transactions on，2006，11（5）：593⁃603.

［5］ Zhang Y，Ge S S，Lee T H.A unified quadratic⁃program⁃ming⁃based dynamical system approach to joint torque optimi⁃zation of physically constrained redundant manipulators［J］. Systems，Man，and Cybernetics，Part B：Cybernetics，IEEE Transactions on，2004，34（5）：2126⁃2132.

［6］ Diftler M A，Mehling J S，Abdallah M E，et al.Robonaut 2⁃the first humanoid robot in space［C］／／Robotics and Automa⁃tion（ICRA），2011 IEEE International Conference on. IEEE，2011：2178⁃2183.

［7］ Albu⁃Schäffer A，Eiberger O，Fuchs M，et al.Anthropomor⁃phic soft robotics⁃from torque control to variable intrinsic com⁃pliance［M］.Robotics research.Springer Berlin Heidelberg，2011：185⁃207.

［8］ 赵建文，杜志江，孙立宁.7自由度冗余手臂的自运动流形［J］.机械工程学报，2007，40（9）：132⁃137. Zhao Jianwen，Du Zhijiang，Sun Lining.Self⁃motion manifolds of a 7⁃DOF redundant robot arm［J］.Chinese Journal of Mechan⁃ical Engineering，2007，40（9）：132⁃137.（in Chinese）

［9］ 张雨浓，谭宁，谭志国，等.基于二次型优化的不定目标自运动规划方案及PA10机械臂仿真验证［J］.暨南大学学报：自然科学与医学版，2010，31（3）：229⁃234. Zhang Yunong，Tan Ning，Tan Zhiguo，et al.Quadratic⁃opti⁃mization based self⁃motion planning with no target⁃configura⁃tion assigned and verified via PA10 simulations［J］.Journal of Jinan University（Natural Science），2010，31（3）：229⁃234.（in Chinese）

［10］ 任子武，王振华，孙立宁.全局和声搜索方法及其在仿人灵巧臂逆运动学求解中应用［J］.控制理论与应用，2012，29（7）：867⁃876. Ren Zhiwu，Wang zhenhua，Sun Lining.A global harmony search algorithm and its application to inverse kinematics problem for humanoid arm［J］.Control Theory＆ Applica⁃tions，2012，29（7）：867⁃876.（in Chinese）

［11］ Eberhart R C，Kennedy J.A new optimizer using particle swarm theory［C］／／Proceedings of the sixth international symposium on micro machine and human science.1995，1：39⁃43.

［12］ 陈鹏，刘璐，余飞，等.一种仿人机械臂的运动学逆解的几何求解方法［J］.机器人，2012，34（2）：211⁃216. Chen Peng，Liu Lu，Yu Fei，et al.A geometrical method for inverse kinematics of a kind of humanoid manipulator［J］. ROBOT，2012，34（2）：211⁃216.（in Chinese）

［13］ Shi Y，Eberhart R.A modified particle swarm optimizer［C］／／Evolutionary Computation Proceedings，1998.IEEE World Congress on Computational Intelligence.，The 1998 IEEE International Conference on.IEEE，1998：69⁃73.

（责任编辑：康金兰）

Self⁃motion Optimization for Redundant Manipulator of Robonaut

LIU Shiping1，HE Xiangyang1，2，HAN Liangliang2，LI Shiqi1，FU Yan1

（1.School of Mechanical Science and Engineering，Huazhong University of Science and Technology，Wuhan 430074，China；2.Aerospace System Engineering Shanghai，Shanghai 201108，China）

The robonaut arm adopts the 7⁃DOF humanoid manipulator to expand its working capabil⁃ity.According to the structural characteristics of the 7⁃DOF S⁃R⁃S humanoid manipulator，the ma⁃nipulator kinematics can be solved with the arm angle parameter method.This method describes the self⁃motion of the redundant manipulator with the arm angle，thus the self⁃motion can be controlled through the quadratic optimization of the arm angle.In order to make the humanoid manipulator in a natural configuration，the indicator named＂Off⁃center Level＂was defined to indicate the degree of deviation from the center of the joint position and the optimal configuration could be described through this indicator，thus a self⁃motion optimization function was established.The particle swarm optimization algorithm with linear inertia was used to find the optimal solution of the self⁃motion opti⁃mization function.The method was tested on the robonaut platform and it could complete the self⁃motion optimization of redundant manipulator quickly and effectively.

redundant manipulator；kinematics；self⁃motion optimization；particle swarm optimiza⁃tion algorithm

TP242.6

：A

：1674⁃5825（2017）02⁃0143⁃07

2016⁃08⁃25；

2017⁃02⁃24

载人航天预先研究项目（030401）；上海航天科技创新基金资助项目（SAST201409）

刘世平，男，副教授，研究方向为智能机械设计与仿真、虚拟样机技术。E⁃mail：liushiping＠mail.hust.edu.cn