顾及空间自相关的地理国情信息统计格网尺度选择——以植被覆盖信息统计为例

连世忠，丁 霖，陈江平

(武汉大学遥感信息工程学院，湖北 武汉 430077)

顾及空间自相关的地理国情信息统计格网尺度选择
——以植被覆盖信息统计为例

连世忠，丁 霖，陈江平

(武汉大学遥感信息工程学院，湖北 武汉 430077)

统计格网尺度的不同会带来统计结果的差异，如何选择统计格网是地理国情信息统计的重要工作。本文提出了一种顾及空间自相关的地理国情信息统计格网尺度选择方法。采用地理国情普查数据，在50 m、60 m、70 m、80 m、90 m、100 m、250 m、500 m和1000 m几个尺度下，以植被覆盖信息统计为例，利用面积占优法和中心点归属法两种方法分别进行格网化，得到了不同尺度的植被格网数据；计算植被覆盖面积统计误差，分析不同尺度下植被覆盖信息的空间自相关的变化特征，并利用Moran’s I系数差值进行尺度选择，得到了植被覆盖信息统计格网的适宜尺度。以龙沙区和清涧县作为研究区域，结果表明，在地理国情植被覆盖信息统计时，不同地区的格网统计适宜尺度是不一样的，植被覆盖度中低的龙沙区的适宜尺度为100 m，而植被覆盖度高的清涧县的适宜尺度为250 m。

空间自相关；尺度选择；统计格网；植被覆盖；地理国情

在地理信息科学中，尺度效应普遍存在，地理信息的尺度效应会对地理现象表达、分析的抽象程度、清晰程度、空间与时间结构模式造成影响[1]。不同空间尺度的地理要素具有不同的性质，空间尺度对于地理要素的研究具有决定意义[2]。地理统计单元作为地理要素统计分析的基础，统计单元的尺度直接决定着统计分析结果的精度和正确性，因此研究统计单元的尺度选择具有重要意义。

在地理格网统计和尺度选择方面，许多学者进行了有意义的研究。QI等[3]利用空间自相关指数研究了尺度变化对景观结构分析结果的影响，其结果表明，随着分析尺度的变化，空间自相关指数也随着变化。曾辉等[4]利用空间自相关分析方法，以深圳市龙华地区为例，对快速城市化景观的空间结构特征及其成因进行了研究。谢花林等[5]开展了区域土地利用变化的多尺度空间自相关分析，以内蒙古翁牛特旗为例进行了空间自相关分析，检验了空间自相关在不同尺度上辨识空间格局的行为和范围。李慧等[6]采用空间自相关分析方法对珠江三角洲土地利用/覆盖变化的空间特征进行了实证研究。综合以上，由于地理数据存在着空间自相关，且空间自相关的大小会随着尺度的变化而改变，而尺度的变化会对统计的结果产生影响，因此，本文研究利用空间自相关进行植被覆盖信息统计的合适尺度选择，并对不同尺度下的格网统计精度进行评估。

关于多尺度数据格网统计误差相关问题的研究，多位学者分别从面积、长度和数量等属性变化探讨了多尺度格网统计的误差问题[7- 11]，并从常规误差分析方面和基于格网的分析方法对误差进行了评定[12- 13]。本文将利用不同尺度下植被覆盖面积总体误差和格网统计误差来评价统计结果，既考虑全局的统计误差，又考虑局部的统计误差。

在地理国情监测统计模型的构建过程中，多源、多属性、多类型、多专题的数据往往有着不同的统计单元。统计单元的不同导致不便于直接利用这些复杂的数据进行统计分析，同时还会影响地理国情监测数据统计分析结果的准确性和一致性。地理格网作为一种科学、统一的空间定位参照系统，是对现有测量参考系统、行政区划参考系统和其他定位系统的补充，将地理国情数据格网化应用到地理国情监测中，可有效解决上述问题。本文提出一种顾及空间自相关的地理国情信息统计格网尺度选择方法。利用地理国情普查试点城市普查数据，在50 m、60 m、70 m、80 m、90 m、100 m、250 m、500 m和1000 m尺度下，分别利用面积占优法和中心点归属法进行格网化处理，研究植被覆盖信息的空间自相关的变化特征，并计算不同尺度和不同格网化方法下植被覆盖信息统计误差和Moran’s I系数差值，分析植被覆盖信息统计格网的尺度适宜性，得到适宜的尺度。

1 研究方法

空间尺度作为空间数据的重要特征，尺度的变化必然会导致地物表达精度的变化，引起空间信息和属性信息发生相应变化[1]。因此，在统计时应当选取适宜尺度的统计格网，以免错误地反映数据实体本身所表现的特性，有效控制数据工作量的增加[14- 15]。

考虑到地理国情普查数据采集标准、研究区数据量大小及处理速度等问题[16]，本文选择在50 m、60 m、70 m、80 m、90 m、100 m、250 m、500 m和1000 m几个尺度下讨论植被覆盖信息在不同格网化方法下的空间自相关，并计算植被覆盖数据随尺度变化的面积误差情况。研究方法具体流程如图1所示，主要包括以下几部分：①试验数据准备；②数据预处理；③不同格网尺度下的植被覆盖面积误差评定及空间自相关分析；④分析得到植被覆盖信息格网统计的适宜尺度。

图1 地理国情植被覆盖信息统计格网尺度选择流程

1.1 数据格网化预处理

数据格网化从本质上来讲是一个从不规则的多边形区域(源区域)到规则的格网区域(目标区域)的转换过程，这种转换不仅包括区域边界形状的改变，还包括源区域到目标区域的属性信息的转换[17]。在空间数据格网化的过程中，应尽量保证生成的格网区域属性的真实性，并且最大限度保留源区域内的属性信息。本文将采用面积占优法(rule of maximum area，RMA)和中心点归属法(rule of centric cell，RCC)两种方法进行植被覆盖数据的格网化预处理，得到不同尺度的植被覆盖格网数据。其中，面积占优法是指由格网区域内占有面积比例最大的源区域的属性值来决定整个格网区域的属性值。在面积占优法中，一个格网单元内如果存在两个或多个优势类型，则随机选择其中之一作为输出单元的类型；中心点归属法是将各个格网区域中心点所在的源区域的属性值作为该格网区域的属性值[18- 19]。图2所示的单个格网单元，内部含有A、B和C这3种地物类型，点O为格网区域中心点。根据面积占优法，格网中A类地物的面积最大，该格网属性代码为A；按中心点归属法，中心点O落在B类地物范围内，此时格网属性赋值为B。

图2 单个格网内不同地类的分布

1.2 尺度选择适宜性的评定方法

为了评估本文尺度选择结果的适宜性及其对统计结果的影响，采用不同尺度下总体误差和格网统计误差进行植被覆盖面积统计误差的评定。以原始数据中植被覆盖面积统计信息作为基准数据，计算不同尺度格网下植被覆盖总面积，并将格网化转换后的面积与基准数据的面积进行比较，从而得到不同尺度下植被覆盖数据的总体面积损失，其计算公式为

(1)

(2)

式中，E为地类的总面积损失；Ag为格网化转换后地类总面积；Ab为基准数据的地类总面积；L为面积损失精度。

在计算格网化预处理过程中的总体面积损失精度的同时，考虑到局部误差可能导致某些细节信息丢失或错误，为避免误差的“此消彼长”问题，针对局部各个格网内的统计误差，利用原始数据中植被覆盖面积信息，分别计算各个格网中误差di，得到不同尺度下的植被覆盖数据的格网统计误差，其公式如下

(3)

(4)

式中，di为格网i中地类的面积损失；d+表示损失为正值；d-表示损失为负值；Z为格网i中地类面积实际值；Zi为格网化预处理后格网i中地类面积统计值。

1.3 利用空间自相关选择合适的格网尺度

根据地理学第一定律，植被覆盖数据存在着空间自相关，属性值随着测定距离的缩小而变得更相似或更不同。具体来说，在不同尺度下，植被覆盖数据具有不同的空间自相关，植被覆盖数据目标区域的属性值会受到邻域区域的影响。因此，在利用不同尺度的格网单元进行植被覆盖信息统计时，可以根据空间自相关随尺度的变化趋势来选择合适的格网尺度。

空间自相关分析是检验具有空间位置的要素的观测值是否显著地与其相邻空间点上的观测值相关联[20]。空间自相关所统计的内容包括空间对象的空间位置和属性，即每个对象与其他相邻统计分析对象之间的空间位置关系及属性取值特征。表示空间自相关的指标和方法很多，其中最常用的是Moran’s I系数。Moran’s I系数用来反映空间邻接或空间临近的区域单元属性值的相似程度，其值在-1～1之间。大于零则表明存在正相关，反之为负相关，等于零则表明不存在空间相关性。其计算公式[21]如下

(5)

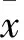
本文采用GeoDa软件进行空间自相关分析，选取各格网内的植被覆盖面积作为各格网的属性值，分别计算在不同尺度下格网数据的Moran’s I系数值，分析空间自相关随格网尺度的变化规律；并计算格网化后与原始植被覆盖数据的Moran’s I系数差值，以此来评价不同格网化尺度对植被覆盖数据的空间结构的破坏程度，其计算公式为

S=Ig-Ib

(6)

式中，S为格网化后和原始的植被覆盖数据的Moran’s I系数差值；Ig为格网化后的植被覆盖数据的Moran’s I系数；Ib为原始植被覆盖数据的Moran’s I系数。S值越小，表明在此尺度下格网化后数据的空间结构越接近实际情况，否则反之。

2 试验区域与试验数据

2.1 研究区域概况

本研究以黑龙江省齐齐哈尔市龙沙区和陕西省榆林市清涧县为研究对象，二者为地理国情普查第一批试点城市普查区域。

龙沙区是黑龙江省齐齐哈尔市市辖区之一，位于齐齐哈尔中心城区，北邻建华区，东南西依次与梅里斯达斡尔区、铁锋区、富拉尔基区、昂昂溪区相邻，区划面积122 km2。全区下辖6个街道，40个社区居委会和6个行政村。区内植被覆盖度为50%左右，为植被中覆盖度地区。

清涧县位于黄河陕晋峡谷西岸，榆林东南部与延安交界处。地处东经109°55′27″—110°38′50″，北纬36°57′30″—37°25′。区划面积为1881 km2，占全省土地总面积的0.91%，占榆林市总面积的4.31%。全县下辖7乡8镇1街道办事处，640个行政村，6个居民委员会。县域内植被覆盖度达到95%，为植被高覆盖度地区。

2.2 数据来源

试验所使用的数据集为研究区域内的地理国情普查数据和不同尺度格网单元。具体包括：①龙沙区地理国情普查数据；②清涧县地理国情普查数据；③根据地理国情普查数据采集标准和试验的需要，利用研究区域的边界矢量数据，分别生成龙沙区和清涧县的不同尺度格网数据，并利用面积占优法和中心点归属法对植被覆盖数据进行格网化预处理，得到不同尺度植被覆盖格网数据，包括50 m、60 m、70 m、80 m、90 m、100 m、250 m、500 m和1000 m 9种不同尺度的格网数据。

3 试验结果和分析

3.1 植被覆盖信息统计误差分析

根据式(1)和式(2)， 计算各尺度下龙沙区和清涧县植被覆盖格网数据的植被覆盖面积总体误差，并与实际面积进行对比，计算总体误差L(见表1和图3)。同时，利用式(3)和式(4)计算各尺度下龙沙区和清涧县植被覆盖面积格网统计误差，得到格网统计误差f(见表1和图4)。

区域类型格网化方法1000m500m250m100m90m80m70m60m50m龙沙区总体误差格网统计误差RMA2．732．251．751．071．041．061．141．151．07RCC5．324．452．111．291．361．321．281．301．27RMA49．2441．0033．9424．8824．1823．9423．8023．4923．54RCC59．8752．7342．6430．9429．7728．4728．7828．8628．29清涧县总体误差格网统计误差RMA1．550．490．110．130．150．160．220．100．09RCC3．662．341．211．310．981．081．071．320．94RMA4．894．382．943．033．112．822．832．892．80RCC6．286．583．813．963．973．623．513．523．49

从统计误差结果来看：①与中心点归属法的误差结果相比，在不同尺度下，面积占优法的植被覆盖信息总体误差和格网统计误差都较小，因此面积占优法可以得到较高精度的植被覆盖格网数据，面积占优法更适用于研究区域的植被覆盖数据的格网化处理；②从表1中可以看出，随着尺度的变化，龙沙区植被覆盖面积误差总体上越来越小。在250～1000 m的尺度下，植被覆盖面积发生了明显的变化，总体误差和格网统计误差都较大。而50～100 m的尺度下，植被覆盖面积未发生较大变化，总体误差在1%左右，格网统计误差变化不大；③从清涧县的统计误差结果来看，不同尺度下植被覆盖面积总体误差和格网统计误差都小于10%，在50～250 m尺度下，植被覆盖面积变化较小，误差变化曲线趋于平缓，随着尺度的变化很小。

3.2 不同尺度植被覆盖信息的空间自相关分析

本文不仅统计分析在不同格网化尺度下植被覆盖信息的面积误差，还研究植被覆盖信息在不同尺度下的空间自相关性的变化特征，利用式(5)和式(6)分别计算各尺度格网化后与原始的植被覆盖数据的Moran’s I系数及Moran’s I系数差值(见表2和图5)。

表2 不同尺度格网下植被覆盖Moran’s I系数及Moran’s I系数差值

从统计误差结果来看:①在50～1000 m尺度下，两个研究区域的Moran’s I系数(真值)都为正，且在1%水平上显著，表明植被覆盖数据存在正的空间相关性；②与中心点归属法的误差结果相比，在不同尺度下，面积占优法的植被覆盖信息的Moran’s I系数都更加接近真值，面积占优法对于数据的空间结构破坏较小，因此面积占优法更适合于研究区域的植被覆盖数据的格网化处理；③对于龙沙区，从图5(a)、图5(b)可知，在50～1000 m尺度下，无论是格网化后还是原始植被覆盖数据的Moran’s I系数值均逐渐增大，在50～100 m尺度下，Moran’s I系数值和Moran’s I系数差值变化较小，空间自相关变化不大；④对于清涧县，从图5(c)、图5(d)可知，Moran’s I系数随着尺度变小而逐渐增大，并且在250 m达到稳定状态，Moran’s I系数和Moran’s I系数差值曲线趋于平缓，随着尺度的变化很小。

4 结 论

在地理国情监测中，植被覆盖信息作为重要的地表覆盖信息，对其进行统计分析具有重要意义。利用规则的地理格网来统计植被覆盖信息，既突破了传统的行政区划边界的限制，又可建立自然与社会经济信息的公共载体，实现统一空间基准下的统计和综合分析。

本文研究了植被覆盖信息在不同尺度下的空间自相关变化特征，通过统计植被覆盖数据在不同方法、不同尺度格网化后的总体误差、格网统计误差、Moran’s I系数差值，进行植被覆盖数据统计的合适尺度选择。选取了龙沙区和清涧县两个研究区域，结果表明：在植被覆盖数据格网化处理方面，中心点归属法比面积占优法好，更适合于研究区域植被覆盖数据的格网化处理，格网化产生的面积误差和Moran’s I系数差值均更小；随着尺度的变化，研究区域植被覆盖信息格网化后的总体误差、格网统计误差、Moran’s I系数差值越来越小，龙沙区和清涧县的各误差曲线分别在100 m和250 m尺度下趋于平缓，因此100 m和250 m分别为龙沙县和清涧县在进行地理国情植被覆盖信息统计时的适宜尺度。

图5 不同尺度下格网植被覆盖信息的Moran’s I系数及Moran’s I系数差值

[1] GOODCHILD M F. Scale in GIS: An Overview[J]. Geomorphology, 2011,130(1):5- 9.

[2] 陈述彭. 大比例尺景观制图方法及其实验[C]∥地学探索：地理学. 北京:科学出版社,1992.

[3] QI Y, WU J. Effects of Changing Spatial Resolution on the Results of Landscape Pattern Analysis Using Spatial Autocorrelation Indices[J]. Landscape Ecology, 1996,11(1):39- 49.

[4] 曾辉, 江子瀛, 孔宁宁, 等. 快速城市化景观格局的空间自相关特征分析——以深圳市龙华地区为例[J]. 北京大学学报(自然科学版),2000,36(6):824- 831.

[5] 谢花林, 刘黎明, 李波, 等. 土地利用变化的多尺度空间自相关分析——以内蒙古翁牛特旗为例[J]. 地理学报,2006,61(4):389- 400.

[6] 李慧, 王云鹏, 李岩, 等. 珠江三角洲土地利用变化空间自相关分析[J]. 生态环境学报,2011,20(12):1879- 1885.

[7] 刘明亮, 唐先明. 基于1 km格网的空间数据尺度效应研究[J]. 遥感学报,2001,5(3):183- 190.

[8] 杨存建, 张增详. 矢量数据在多尺度栅格化中的精度损失模型探讨[J]. 地理研究,2001,20(4):416- 422.

[9] GALTON A. Granularity- sensitive Spatial Attributes[J]. Spatial Cognition and Computation,2003,3(2/3): 97- 118.

[10] 赵磊, 孟淑英. 土地利用空间数据尺度转换中的精度损失分析[J]. 国土资源遥感,2009,80(2):45- 48.

[11] 崔步礼, 常学礼, 左登华, 等. 沙地景观中矢量数据栅格化方法及尺度效应[J]. 生态学报, 2009,29(5): 2463- 2472.

[12] 陈建军, 周成虎, 程维明. GIS中面状要素矢量栅格化的面积误差分析[J]. 测绘学报,2007,36(3): 344- 350.

[13] 白燕, 廖顺宝, 孙九林. 栅格化属性精度损失的评估方法及其尺度效应分析——以四川省1∶25万土地覆被数据为例[J]. 地理学报, 2011, 66(5):709- 717.

[14] LI D, SHAO Z, ZHU X, et al. From Digital Map to Spatial Information Multi- grid[C]∥Proceedings of 2004 IEEE International Symposium on Geoscience and Remote Sensing.[S.l.]:IEEE,2004:2933- 2936.

[15] BAKER M,APON A,FERNER C, et al. Emerging Grid Standards[J]. Computer, 2005,38(4): 43- 50.

[16] 刘婷, 刘仁义, 张丰，等. 多级网格环境下的土地利用统计方法[J]. 中山大学学报(自然科学版),2011,50(3):118- 122.

[17] 朱良峰, 吴信才, 刘修国. GIS中矢量多边形网格化问题研究[J]. 地理与地理信息科学,2004,20(1):12- 15.

[18] BIAN L,BUTLER R. Comparing Effects of Aggregation Methods on Statistical and Spatial Properties of Simulated Spatial data[J]. Photogrammetric Engineering and Remote Sensing, 1999, 65(1): 73- 84.

[19] HE H S, VENTURA S J, Mladenoff D J. Effects of Spatial Aggregation Approaches on Classified Satellite Imagery[J]. International Journal of Geographical Information Science, 2002, 16(1): 93- 109.

[20] MARTIN D. An Assessment of Surface and Zonal Models of Population[J]. International Journal of Geographical Information Systems, 1996, 10(8): 973- 989.

[21] MORAN P A P. Notes on Continuous Stochastic Phenomena[J]. Biometrika, 1950,37(1- 2): 17- 23.

Scale Selecting of Geographic National Conditions Information StatisticalGrids with Spatial Autocorrelation ——A Case Study ofVegetation Cover Information Statistics

LIAN Shizhong,DING Lin,CHEN Jiangping

(School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430077，China)

The difference in statistical grid scales will bring different statistical results, so it is important to select statistical grids for the geographical conditions information statistics. A method of choosing statistical grids scale of geographical conditions information with spatial autocorrelation being taken into account is proposed. By using geographic conditions census data and taking vegetation cover information statistics as an example, the study gets vegetation cover girds data, under the rule of maximum area and the rule of centric cell in scales of 50 m, 60 m, 70 m, 80 m, 90 m, 100 m, 250 m, 500 m and 1000 m, and meanwhile calculates vegetation cover statistical errors， analyzes changes of spatial autocorrelation of vegetation cover gird data at different scales to make scale selection, and then uses vegetation cover statistical errors to obtain an appropriate statistical grid scale of vegetation cover information statistics. The results show that for vegetation cover information statistics of geographic national conditions, the suitable scale is 250 m in areas with high degree of vegetation coverage, and 100 m in areas with low degree of vegetation coverage.

Spatial autocorrelation; scale selecting; statistical grids; vegetation cover; geographic national conditions

2016- 04- 12

国家自然科学基金重点项目(41331175) 作者简介： 连世忠(1990—)，男，硕士生，工程师，主要从事地理国情监测数据分析与评价方面的工作。E- mail：371664651@qq.com 通信作者： 丁 霖。E- mail：dinglin@whu.edu.cn

连世忠，丁霖，陈江平.顾及空间自相关的地理国情信息统计格网尺度选择——以植被覆盖信息统计为例[J].测绘通报，2017(3)：46- 51.

10.13474/j.cnki.11- 2246.2017.0082.

P208

A

0494- 0911(2017)03- 0046- 06