混沌粒子群算法在应急资源调度中的应用

张永领，马 娇

(河南理工大学 应急管理学院,河南 焦作 454000)

混沌粒子群算法在应急资源调度中的应用

张永领，马 娇

(河南理工大学 应急管理学院,河南 焦作 454000)

为更科学合理的解决应急资源的调度问题，根据连续性消耗应急问题的特点，建立了以出救活动总成本最小为目标的应急物资优化调度模型；针对模型的非线性特点，提出了基于混沌粒子群算法的应急资源调度模型并给出了求解方法；最后用算例验证了模型的合理性及算法的有效性。计算结果表明将混沌粒子群算法用于求解多约束条件的应急物资调度问题，可以在一定程度上克服基本粒子群算法容易陷入局部最优解的不足，算法收敛速度更快且精度更高，是解决应急资源调度路径问题的一种有效方法。

调度；应急物资；连续型消耗；混沌粒子群；路径

近年来，各种自然灾害和突发事件在全球范围内频繁发生，严重威胁着人们的生命和财产安全。灾害尤其是巨灾一旦发生对应急资源的需求量就会急速增加，这就需要将应急资源快速合理地运送到各个受灾点，以降低灾害造成的损失。应急物资是减少人员伤亡、降低财产损失的基本保障，因此如何对应急物资进行科学合理的调度具有重要现实意义。

由于科学的应急物资调度是灾害应急救援的保障，因此应急物资调度受到国内外学者的普遍关注，如Kemball-Cook等于1984年首先提出了需要对应急物资的调度进行针对性的研究[1]；Linet等建立了一个以最小应急时间为目标的数学模型，用于处理应急物资的调度问题[2]；Barbarosoglu等研究了在需求时间最小的情况下，成本最小的应急资源调度模型[3]；黄洪涛提出将应急物资分为短暂性消耗物资和长期性消耗物资两种类型进行了调度研究[4]；刘春林等建立了连续性消耗应急物资调度模型，并证明了模型的合理性[5]；姜昌华研究了遗传算法在物流系统优化中的应用[6]。

目前对于应急资源调度问题的建模大多局限于对单一目标进行研究，对于模型的求解方法也存在各自缺陷。胡飞虎等采用遗传算法解决应急物资的调度问题，但该算法通用性差无法被广泛应用[7]；田军等研究了应急物资配送的动态调度方法，但该算法的计算复杂度较高，极大地限制了其实际应用[8]；左春荣等研究了基于粒子群算法的多应急点资源调度问题，但该算法存在容易陷入局部最优解的缺陷[9]。为此，本文将以连续性消耗应急系统为背景，建立多出救点、多应急资源需求约束、时间约束等多约束条件下的应急资源调度模型，采用混沌粒子群算法对模型进行求解，克服了以往进行应急资源调度研究中采用基本粒子群算法容易陷入局部最优解的不足，可以在很大程度上降低计算程序中的迭代步数，提高求解效率，验证了模型的合理性及算法的优越性。

1 应急资源调度

1.1 应急资源的内涵

应急资源是指在突发事件应急处置所需要的各类物资的统称。广义的应急资源包括防灾、应对、恢复等环节所需要的各类物资。狭义的应急资源仅指应急救援过程所需要的各种物资保障。应急资源不同于一般物资它具有以下几个特征。

(1)时效性。时效性是指应急资源应在突发事件发生后及时送达指定地点。因为灾害发生后的72h是救援的“黄金时间”，在“黄金时间”段内，应急资源应到达受灾地区，否则可能就会失去了其应急的意义。

(2)不确定性。突发事件类型、发生的事件、地点以及级别具有不确定性，对应急物资需求的种类和数量也具有不确定性。这种不确定性具体表现在两个方面，一是需求时间、地点的不确定性，应急部门无法预测到需求的时间、地点，做到提前的调度；二是需求的品种和数量的不确定性，突发事件的类型、级别、发生地点的不同决定了需求的种类和数量也存在很大的差异。

(3)弱经济性。应急资源最重要的特点就是要起到“应急”的作用。在实际的应急处置工作中，要求在既定的时间内满足灾民对物资的需求。所以在应急物资的筹集、调度和配置上都是以最短时间为核心的。在应急资源调度的研究上虽然也有考虑到费用最小问题，但都是在时间约束的条件下进行的[10]。

1.2 应急资源调度的特点

当突发事件发生后，在应急物资的种类繁多以及多出救点和多受灾点的情景下，政府应急管理部门需要制定出科学合理的调度方案，确保资源的及时到达，使应急救援得以有序进行。处置突发公共事件中的应急资源调度与一般事件中的资源调度相比具有以下几方面的特点。

(1)事件约束性。突发事件发生以后，为了保障应急救援的顺利进行，应急资源调度需要在有效时间内或规定事件内完成，以最大限度的减少人员伤亡和财产损失。因此调度时间就成了应急资源调度考虑的首要条件，即应急物资调度必须考虑调度的时效性，及时准确地将所需应急资源运送到指定地点。

(2)动态性。突发事件大小规模不一，种类各异，对应急资源的需求具有不确定性；而且衍生和次生的灾害有时也难以把握；再加之事件处置的每个阶段所需要的应急物资也各不相同。这就需要根据救援现场的实际情况及时不断的调整调度方案，以满足突发事件处置的动态需求。

(3)整合和协同性。当灾害尤其是巨灾发生后，对某些物资的需求急剧增加，政府部门所储备的应急物资难以满足应急需求，这就需要在应急物资调度时综合考虑政府应急物资储备、非政府机构如慈善机构以及其他社会资源，整合各类物资进行综合配置和科学调度。

一般意义上的物资调度问题是指把物资从存储地运送到需求地，它是以成本最小为目标函数。而在应急管理中，救援物资的调度首先考虑的是物资的时效性问题，即在最短的时间内把物资运输到指定的灾区，保证其能及时的投入到救援活动中。在应急物资调度过程中也考虑成本问题，但是是在保证时间最小化的前提下尽量使成本最小化。

2 应急物资调度模型构建

2.1 问题描述及假设

当灾害发生时，一方面在资源储备有限的情况下需要从多个供应点调集资源；另一方面要保证在任何时刻都不能出现因物资供应不足引起的应急活动的停止[11]。因此应急资源调度优化需解决3个关键问题：①应急物资的优化配置问题。根据有限的物资储备，在多个物资供应点间进行物资科学合理调配，使得各应急点物资需求满足量最小化。②时间约束问题。在满足各应急点应急物资需求的前提下，对突发应急事件的物资救援时间最早。③应急成本问题。灾害环境下调度路线的选取除了考虑时间因素外，还应考虑到出救活动的总成本问题。

灾后应急资源优化调度属于大空间尺度下的资源宏观调度优化，与微观物流具有较大不同，故作如下假设[12-13]：

(1) 设从突发事件发生时刻到应急活动开始时刻，没有因施救不及时而造成损失；

(2) 如需从出救点调配应急物资，则调配数量须大于起始运输量下限；

(3) 应急活动开始后，各出救点间不存在资源的相互调度。

2.2 应急物资优化调度模型建立

本文以连续消耗型应急活动为背景[14]，从应急系统固有成本和因施救不及时造成损失的角度考虑,建立了以出救活动总成本最小为目标的多出救点、多应急资源约束和时间约束的应急物资调度模型。

设应急系统中有n个出救点，m种应急物资，应急物资调度数学模型如下：

(1)

对于因应急物资缺失而产生的损失费用本文从以下三种情况进行考虑[15]:

(1) 第i时刻各个应急点各类物资均充足时，即缺失量为0，则因应急物资缺失而产生的损失费用Eij=0。

(2) 当第i时刻第j类资源已经缺失，即Ij(ti)<0，此时:

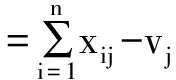
(2)

在周期[ti,ti+1]内，Eij为：

(3)

(4)

(5)

在周期[ti,ti+1]内，Eij为：

(6)

3 混沌粒子群算法求解

混沌粒子群算法源于对鸟群捕食行为的研究，Eberhart和Kennedy于1995年提出了一种基于随机群体的新型智能优化方法的粒子群算法(ParticleSwarmOptimization,PSO)用于指导优化搜索[16-17]。

3.1 基本粒子群算法

在PSO算法中，每个基本粒子(Particle)代表一个可能的解且有一个由被优化了的函数决定的适应值(Fittness)，所有的粒子组成一个群体(Swarm)。粒子在解空间内根据自身的飞行经验和群体经验共同来决定下一步的飞行速度和方向，以此来寻找最优解。

假设在d维搜索空间内进行求解，群体由n个基本粒子组成，

(7)

(8)

(9)

式(8)、式(9)分别描述了该粒子在每一维空间上的运动情况。在每一次进化中，每个粒子通过追踪两个局部最优解来更新自己，一个是粒子本身所找到的最优解(pBest)，Pi={Pi1,Pi2,…,Pid}，另一个是目前整个群体所找到的最优解(gBest)，粒子根据如下公式来对自己的位置和速度进行更新：

(10)

式中：w为惯性权重，c1和c2为学习因子，r1和r2为(0,1)之间的随机数。

基本粒子群算法结构简单、易于实现，但也存在以下不足：① 算法的初始化和进化过程均具有随机性特点，对个体质量难以保证，群解中一部分远离全局最优解的局部最优解会影响进化过程的收敛；② 当粒子的自身信息及个体极值信息占绝对优势时，该算法容易陷入局部最优解。

3.2 混沌粒子群算法

针对基本粒子群算法的不足，本文采用一种基于混沌化思想的粒子群优化算法，其基本思想如下：

(1) 利用混沌运动的遍历性及对初值极为敏感的特点，从一系列随机产生的初始解中择优选出初始群体，提高种群的多样性和遍历性。

(2) 每个粒子的惯性权重根据其适应值来进行自适应调整，从而提高算法的“全局粗略探测”和“局部精细挖掘”能力。

(3) 从当前种群中选取一部分适应值较大的粒子进行混沌优化，以此增强算法跳出局部最优解的能力，进而提高其全局搜索能力。

混沌一般是由确定性方程通过映射得到的具有随机性的运动状态，Logistic映射便是一个典型的混沌系统，其搜索算法步骤如下：

(11)

式中：xmax,j和xmin,j分别为j维变量的搜索上下界。

(2) 计算混沌变量，

(12)

(13)

3.3 算法步骤

混沌粒子群算法的程序流程图如图1所示。

混沌粒子群算法步骤如下：

(1) 初始化种群中每个基本粒子的位置和速度；

(2) 计算每个粒子的适应度，对每个粒子的个体极值pBest及种群极值gBest赋初值；

(3) 更新粒子的个体极值和种群极值；

(4) 对种群中的最优粒子进行局部混沌搜索；

(5) 更新下一代种群中粒子的个体极值和种群极值；

(6) 判断是否满足条件，若满足则获得最优解gBest；否则，令k=k+1，流程转向步骤(2)。

4 算例分析

为考察上述模型的合理性及算法的可靠性，用Matlab7.0分别编写了基于混沌粒子群算法和粒子群算法的应急物资优化调度问题求解程序，并在同一计算机上进行运行。

设某地区发生自然灾害，在应急救援的过程中急需5种应急物资可从10个出救点进行调配。应急物资需求量为X=(70,80,50,60,80)，物资消耗速率为V=(3,5,4,3,7)，物资缺失单位时间内损失费用为D=(7,2,9,5,12)，应急活动终止时间T为1 000，起始运输量下线x0=2，各出救点的物资可供应量如表1所示，物资到达应急地点的所需时间和单位成本如表2所示。制定应急资源调度方案在满足事故应急救援基本需求的情况下系统总出救成本最小。

图1 混沌粒子群算法流程图

A1A2A3A4A5A6A7A8A9A10Xi151395108137116Xi248717510415139Xi311851371036812Xi4961016819102076Xi512915104221291510

表2 物资到达应急地点的所需时间和单位成本

粒子群算法参数：粒子数n=50；学习因子c1=c2=2；惯性权重w=0.8；最大迭代数200。

混沌粒子群算法参数：粒子数n=50；学习因子c1=c2=2；惯性权重w=0.8；混沌最大迭代步数为10，粒子群最大迭代步数取200。

由基本粒子群算法得出的最佳调度方案为：

相应的最小出救成本为Z=781 263。由混沌粒子群算法得出的最佳调度方案为：

相应的最小出救成本为Z=729125。

基本粒子群算法和混沌粒子群算法的目标函数收敛曲线如图2所示，纵轴表示出救费用，以10万元为单位，横轴表示迭代次数。从图2可知，对于应急资源优化调度问题，标准粒子群算法在第130代左右收敛，混沌粒子群算法在第45代左右收敛且结果更优，结果表明混沌粒子群算法求解效率及精度均明显优于基本粒子群算法。

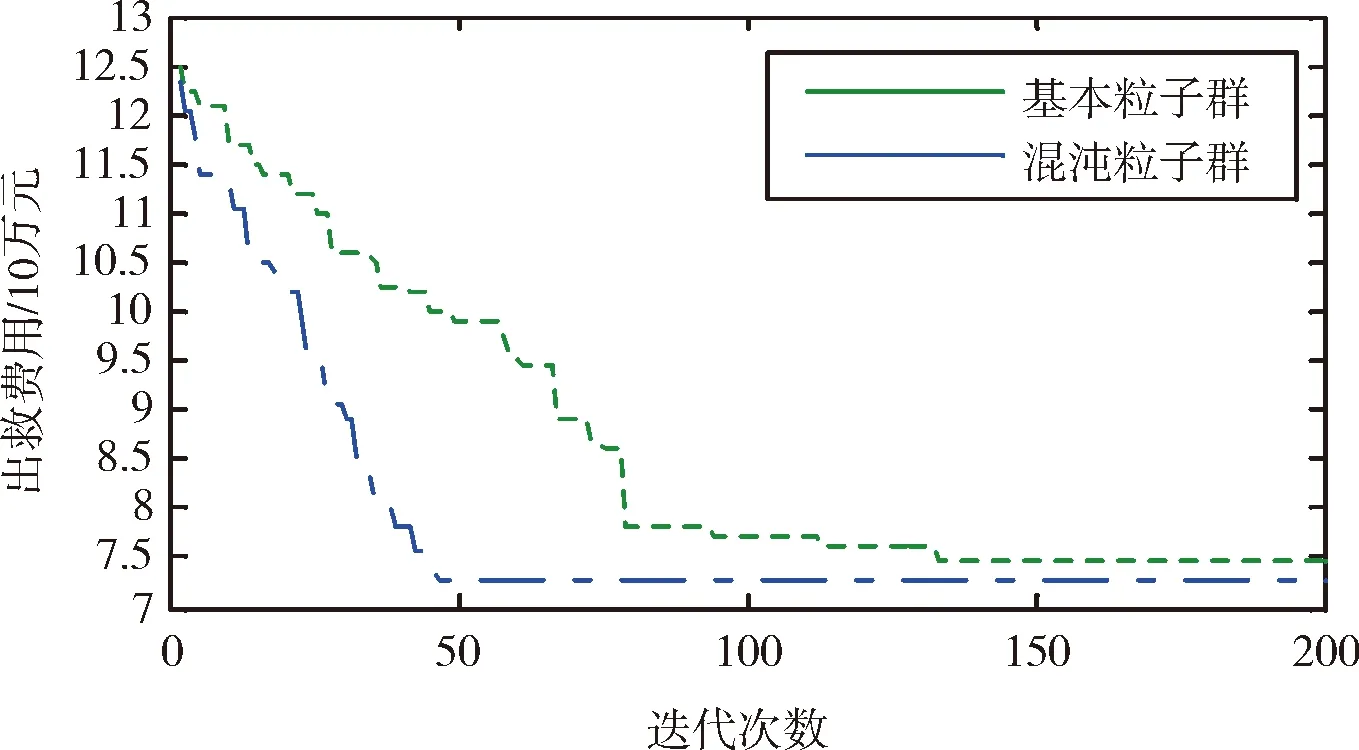
图2 不同算法下目标函数的收敛曲线

5 结语

应急物资的及时供应是灾害救援的物质基础。对于突发事件的应对处置实际上就是一个连贯的合理的应急物资协调与调度的过程。本文以连续性消耗应急系统为背景，在充分考虑出救固有成本及因施救不及时所造成损失费用的基础上，建立了以出救活动总成本最小为目标的多出救点、多应急资源约束和时间约束的应急物资调度模型，针对模型的非线性特点及基本粒子群算法容易陷入局部最优解的不足，设计了基于混沌粒子群算法的调度模型，并给出了求解方法和步骤，最后用算例验证了模型的合理性及求解算法的优越性。

本文所设计的调度模型便于使用计算机求取更优解，所采用的混沌粒子群算法与单纯的粒子群算法相比求解效率更高且结果更优，是解决应急资源调度路径问题的一种有效方法。

[1] Kemball-Cook D, Stephenson R. Lesson in logistics from Somalia[J]. Disaster, 1984,8(1):57-66.

[2] Linet O, Ediz E, Beste K. Emergency logistics planning in natural disasters[J]. Annals of Operations Research, 2004,129(7):217-245.

[3] Barbarosoglu G, Arda Y. A two-stage stochastic programming framework for transportation planning in disaster response[J]. Journal of the Operational Research Society,2004,55(1):43-53.

[4] 黄洪涛.应急物流系统研究[D].大连:大连海事大学,2006.

[5] 刘春林,何建敏,施建军.一类应急物资调度的优化模型研究[J].中国管理科学，2001,9(3):29-36.

[6] 姜昌华.遗传算法在物流系统优化中的应用研[D].上海:华东师范大学,2007.

[7] 胡飞虎,田朝辉,李威,等.基于遗传算法的应急物资分层调度研究[J].计算机工程,2015,41(10):53-58.

[8] 田军,马文正,汪应络,等.应急物资配送动态调度的粒子群算法[J].系统工程理论与实践,2011,31(5):898-906.

[9] 左春荣,周玉琴.基于粒子群算法的多应急点资源调度研究[J].微电子学与计算机,2012,29(7):135-137.

[10]唐伟勤,张敏,张隐,大规模突发事件应急物资调度的过程模型[J].中国安全科学学报,2009,19(1):33-37.

[11]唐伟勤.大规模突发事件应急物资调度基本模型研究[D].武汉:华中科技大学,2009.

[12]文仁强,钟少波,袁宏永,等.应急资源多目标优化调度模型与多蚁群优化算法研究[J].计算机研究与发展,2013,50(7): 1464-1472.

[13]庞海云,刘南,吴桥.应急物资运输与分配决策模型及改进粒子群优化算法[J].控制与决策,2012,27(6):871-874.

[14]Marina Yusoff, Junaidah Ariffin, Azlinah Mohamed. A Two-tier Solution for Disaster Relief Management[C]// 2013 IEEE Symposium on Industrial Electromics and Applications, Kuching, Malaysia, 2013,9.

[15]潘郁,余佳,达庆利.基于粒子群算法的连续性消耗应急资源调度[J].系统工程学报,2007,22(5):556-560.

[16]龚纯,王正林.精通MATLAB最优化计算(第二版)[M].北京：电子工业出版社，2012.

[17]周孝法,陈陈,杨帆,等.基于自适应混沌粒子群优化算法的多馈入直流输电系统优化协调直流调制[J].电工技术学报,2009,24(4):193-200.

Emergency Resources Scheduling Based onChaotic Particle Swarm Optimization

ZHANG Yongling and MA Jiao

(HenanPolytechnicUniversity,EmergencyManagementSchool,Jiaozuo454000,Henan)

Amorescientificandreasonablesolutiontotheemergencyresourceschedulingproblem,accordingtothecharacteristicofcontinuousconsumptionemergencyproblem,aoptimizationschedulingmodelisproposedaimsatminimizingthetotalcost;Inviewofthenonlinearcharacteristics,achaoticparticleswarmalgorithmanditsstepsisproposedtoimprovetheabilitytofindthebestswarmandavoidbeingtrappedinlocalminima;Finally,thepracticalexampleispresentedtoverifythevalidityofthemodelandalgorithm,anditisshownthatthealgorithmisbetterthantraditionalparticleswarmoptimizationtodealwithemergencysuppliesschedulingproblemwithmulticonstraintconditions.Itisaneffectivewaytosolvetheproblemofemergencyresourceschedulingpath.

scheduling;emergencysupplies;continuousconsumption;chaoticparticleswarm;thepath

10.3969/j.issn.1000-811X.2017.02.032.]

2016-08-13

2016-10-08

2012年河南省高校科技创新人才项目“基于情景分析的应急物资保障能力评价研究”

张永领(1975-),男,山东成武人，博士，副教授,主要从事应急管理研究.E-mail:zhyongling@126.com

X43；N945.25

A

1000-811X(2017)02-0185-05

10.3969/j.issn.1000-811X.2017.02.032

张永领，马娇. 混沌粒子群算法在应急资源调度中的应用[J]. 灾害学，2017，32(2)：185-189. [ZHANG Yongling and MA Jiao.Emergency Resources Scheduling Based on Chaotic Particle Swarm Optimization[J]. Journal of Catastrophology，2017，32(2)：185-189.