分位数法对多指标干旱等级划分一致性的作用
孙洪泉,吕 娟,苏志诚,宋苏林,王亚许
(1. 中国水利水电科学研究院,北京 100038;2. 水利部防洪抗旱减灾工程技术研究中心,北京 100038;3. 济南市水文局,山东 济南 250099)
分位数法对多指标干旱等级划分一致性的作用
孙洪泉1, 2,吕 娟1, 2,苏志诚1, 2,宋苏林3,王亚许1, 2
(1. 中国水利水电科学研究院,北京 100038;2. 水利部防洪抗旱减灾工程技术研究中心,北京 100038;3. 济南市水文局,山东 济南 250099)
为了准确掌握干旱严重程度,制定合理的抗旱减灾对策,通常采用多种干旱指标进行旱情评估。然而,多指标干旱划分的干旱等级结果往往存在不一致性,比如某指标评估干旱为轻度,另一指标评估干旱为严重。这种不一致性的原因之一是干旱指标的阈值设定不合理。传统的阈值分割法划分干旱等级受主观经验影响较大,缺乏统一的标准。该文提出采用分位数方法对多指标进行干旱等级划分的思想。针对标准化降水指数和降水距平百分率指数,分别采用传统的阈值分割法和分位数法划分干旱等级,并对结果进行一致性检验和分析。结果表明:分位数法划分多指标干旱等级,得到的结果具有较高的一致性;分位数方法具有广泛的适用性,能够用于多种指标的等级划分;分位数法确定的阈值是随着干旱的季节特性和区域特性动态变化的,具有物理和统计意义。
分位数;干旱等级划分;多指标;阈值分割;一致性;标准化降水指数;降水距平百分率
干旱是世界上造成损失最严重的自然灾害之一[1],准确掌握旱情的发生、发展,对制定合理的抗旱减灾对策,减轻干旱灾害损失和影响具有重要的意义。通常采用各种干旱指标用于定量评估干旱的严重程度、历时长短和发生频率[2],如常用的降雨异常指数(Rainfall Anomaly Index, RAI)[3],标准化降水指数(Standardized Precipitation Index, SPI)[4],降水距平百分率(Percentage of Precipitation Anomalies,PPA)[5],帕尔默干旱指数(Palmer Drought Severity Index, PDSI)[6],地表水分供应指数(Surface Water Supply Index,SWSI)[7],作物墒情指数(Crop Moisture Index, CMI)[8],植被状态指数(Vegetation Condition Index, VCI)[9]等。由于干旱具有发生发展过程缓慢、影响因素较多和非结构化的特点,任何单一指标都无法准确评估干旱的严重程度[10-11]。因此,现实中普遍采用多种指标进行旱情评估,利用给定的阈值将干旱的严重程度划分为若干等级,通过多指标结果的综合作为最终的评估结果[12]。然而,多指标干旱评估往往存在结果不一致性,比如某指标评估干旱为轻度,另一指标评估干旱为严重。
这种不一致性是由两方面的原因导致。一方面是指标的物理意义不同。比如,SPI指数是通过分析降雨的概率分布情况,SWSI指数则考虑地面的分亏缺情况,由于水文干旱比气象干旱具有时间上的延迟,因此二者评估的干旱必然不一致[2]。另一方面是干旱等级划分时的阈值设定不合理所致。通常的干旱等级划分是根据各指标的阈值区间进行干旱评估,即“阈值分割法”。由于干旱缺乏普遍接受的统一定义[10],各指标划分干旱等级的阈值通常是根据经验和统计所得,存在一定程度的主观任意性,因此导致不同指标得到的干旱等级存在较大差异。比如,SPI指数和PPA指数均是降雨因子的干旱指数,二者具有相同的物理意义,反映的干旱严重程度应具有较好的一致性。而实际上,两种指标的干旱等级结果常常差异较大。这是因为SPI指数和PPA指数的阈值设定没有统一的参考依据,得到的干旱等级存在不一致性。
为了寻找合理的阈值设定方案,解决多指标干旱评估结果不一致的问题,本研究将详细分析分位数[13]思想在多指标干旱等级划分中的应用。分位数法广泛应用于洪水、干旱、飓风等的等级划分和频率分析[14],其基本思路是计算某指标的历史序列值,将当前指标值在历史序列值中进行排序,根据其所处的分位数进行等级划分。本研究以SPI指数和PPA指数为例,利用分位数法和传统阈值分割法分别对其进行干旱等级划分,并对结果进行一致性分析,以此阐述分位数方法在干旱等级划分中的应用。
1 研究方法
1.1 分位数
分位数,亦称分位值、分位点,是指将一个随机变量的概率分布范围分为几个等份的数值点,常用的有中位数(中值)、四分位数、百分位数等。其定义为:当随机变量X的概率密度函数为Pr(X),若变量x满足
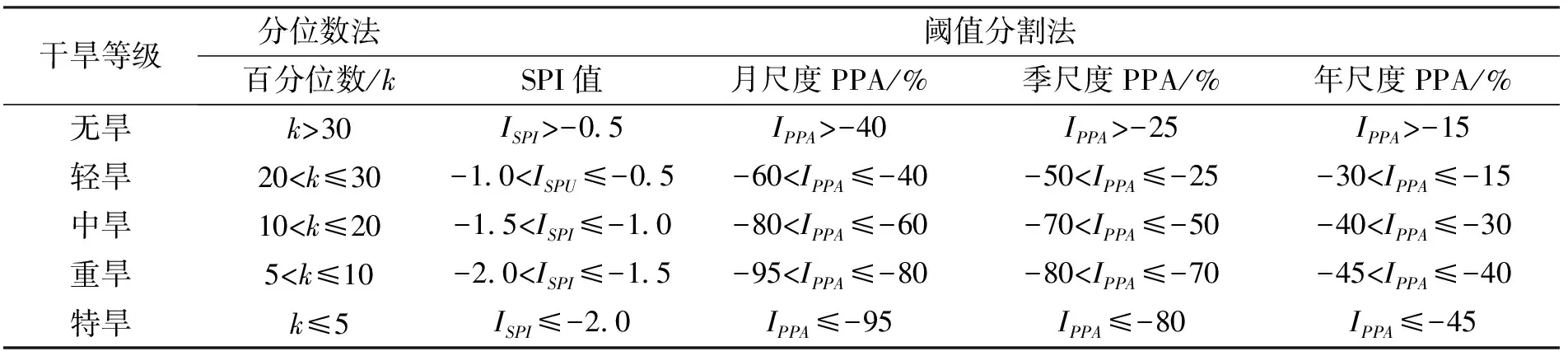
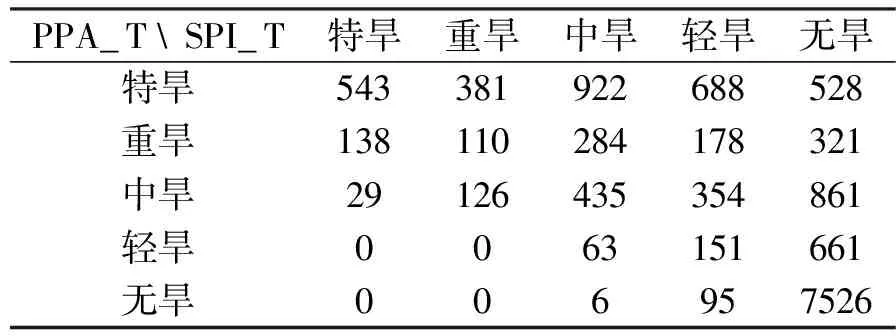
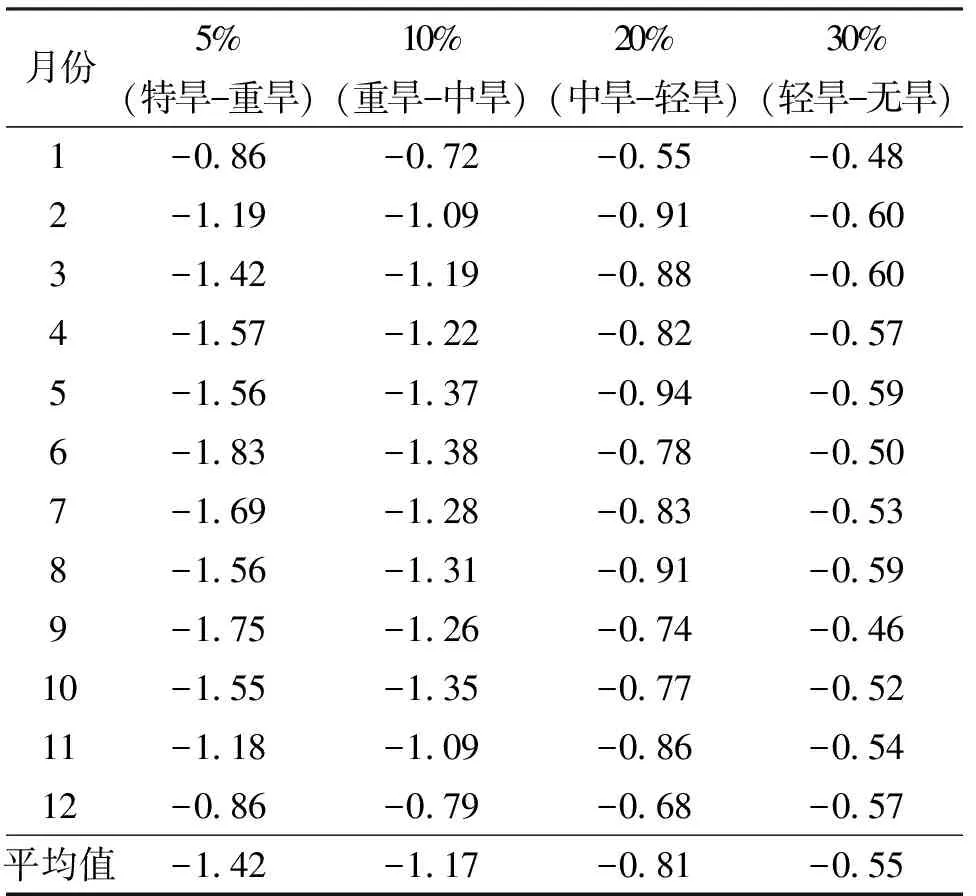
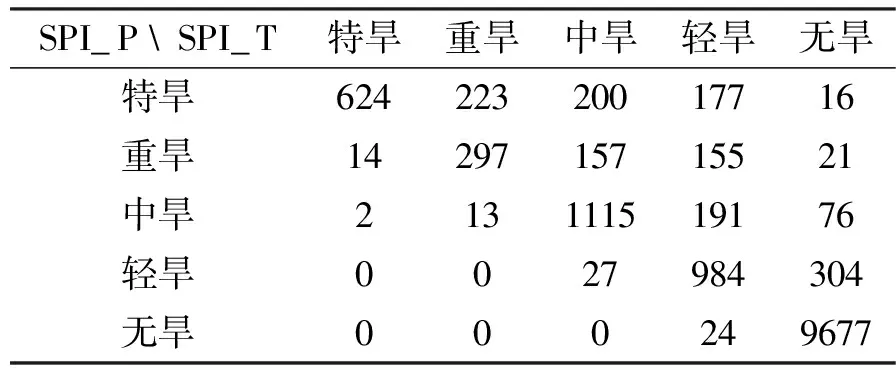
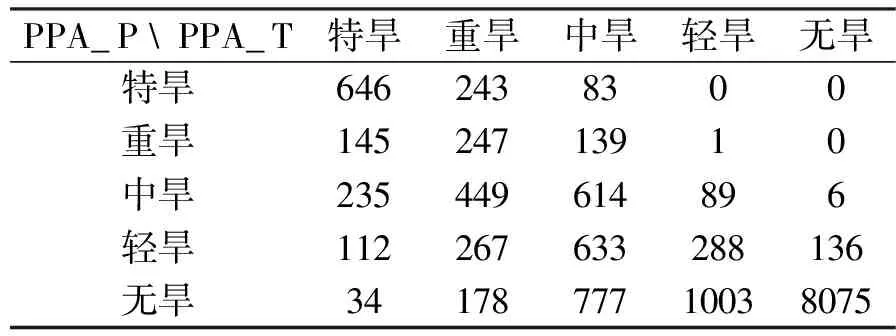
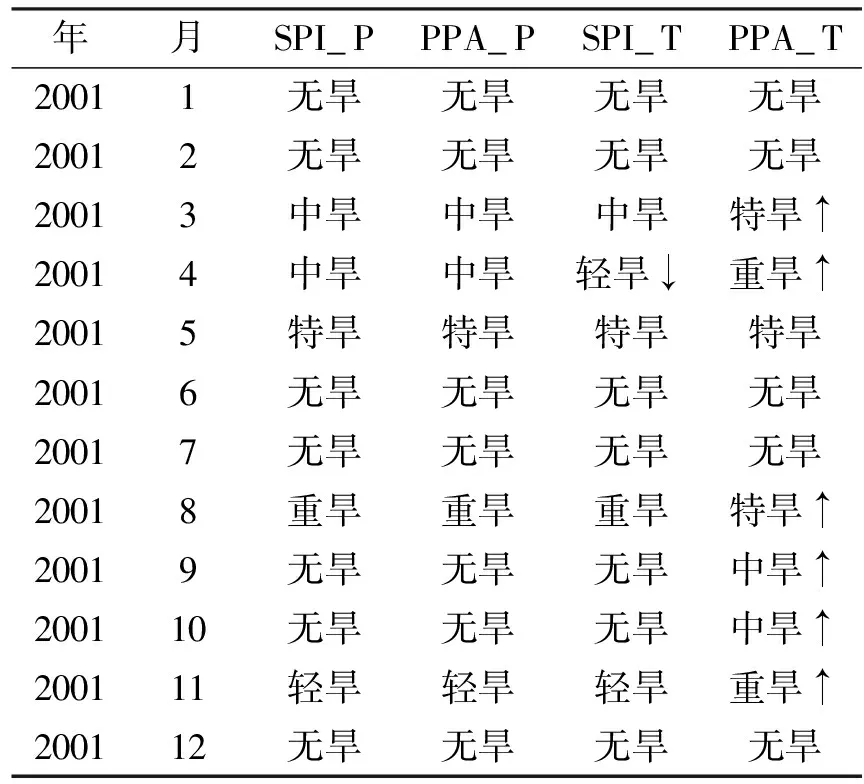
Pr(X (1) 则,x为X的第k个q分位数对应的值,记为xk。 对于有限离散样本空间,样本数量为N,将随机变量X按照从小到大的顺序依次标记为X1,X2,…,XN,则xk可以通过Ik=Nk/q计算而得,即寻找X1,X2,…,XN中对应的第Ik个值。 通常,如果q=4,称为四分位数;如果q=100,称为百分位数。本研究中选用百分位数进行干旱等级的划分,将干旱指数按照从小到大的顺序依次排列,则处于k%位置的值为第k个百分位数。如果给定百位数值σ1和σ2作为阈值,规定满足σ1 1.2 干旱指标 本研究采用SPI和PPA指数进行研究。SPI由Mckee等人[4]提出,其物理意义是假设降水分布服从Γ分布,在将其正态标准化后,实测降水量相对降水概率分布函数的标准偏差即为SPI指数,详细计算参考[15]。 降水距平百分率(PPA)是指某时段的降水量与常年同期状态的偏离程度,其计算方法为: (2) 1.3 一致性检验 采用分位数方法和阈值分割方法对SPI和PPA指数进行干旱等级划分,比较干旱识别的等级是否一致,采用科恩(Cohen)Kappa系数[16]和总体精度(OverallAccuracy)进行一致性检验。 (1)Kappa系数[16]的数学表达为: (3) 式中:n,nα和nε分别为总样本量、观测一致样本量和期望一致样本量。pα=nα/n,是观测一致率;pε=nε/n,是期望一致率,即由于偶然机会造成的一致率。具体过程中,Kappa系数通过混淆矩阵[17]计算,详细算例见3.1所示。 当两个分类完全一致时,nα=n,nε=0,此时κ值为1;当观测一致率大于期望一致率时,κ值为正数,且κ值越大,说明一致性越好。当观察一致率小于期望一致率时,κ值为负数,这种情况一般来说比较少见。根据边缘概率的计算,κ值的范围值应在[-1,1]之间。κ≥0.75两者一致性较好;0.4≤κ<0.75两者一致性一般;κ<0.4两者一致性较差[18]。 (2)总体精度的计算如下: (4) 总体精度虽然也指示一致性的高低,但相较Kappa系数通过混淆矩阵反映各个类别之间的差异而言,其一致性评判的表现力有所欠缺。因此本研究以Kappa系数为主要评价指标,总体精度的结果作为经验参考。 2.1 数据 本研究选择济南市8个站点1965年1月至2014年12月共4 800条月降雨资料进行分析。济南市位于山东省中部,面积约8 200km2,属暖温带半湿润大陆性季风气候区,多年平均降水总量638mm。受地理位置及季风气候影响,济南市旱灾多发生在春、秋季,时有春夏连旱。 通过对8个站点的月降雨数据进行P-III型降雨分布拟合,发现各站点基本服从相同的降雨分布(结果未在此列出),因此可以将各站点数据汇集在一起进行分析。为了反映不同时间尺度的干旱特性[2],采用1个月(月尺度)、3个月(季尺度)和12个月(年尺度)时间尺度的干旱指标进行分析。 表1 干旱等级划分依据 2.2 干旱等级划分 我国出台的《GB/T 20481-2006 气象干旱等级》[19]和《GB/T 32135-2015 区域旱情等级》[20]将干旱等级划分为无旱、轻旱、中旱、重旱和特旱共5个等级,并给出了SPI指数和PPA指数的参考阈值。本研究中阈值分割方法根据上述两种标准进行阈值区间的设置。分位数方法根据文献[14]确定各等级的分位数区间。具体干旱等级划分依据如表 1所示。 由于PPA指数受时间尺度的影响,因此采用阈值分割法时,1个月、3个月和12个月将分别采用月尺度、季尺度和年尺度的不同阈值区间进行干旱等级划分。SPI指数不同时间尺度的阈值一致。分位数方法是根据指标值在历史同期序列中的百分位数进行等级划分,任何干旱指标都根据统一的分位数区间划分干旱等级。 3.1 一致性检验 采用分位数方法对SPI和PPA指数的干旱识别结果进行一致性检验分析(SPI_P和PPA_P)。表2是对应的混淆矩阵,纵向为SPI划分的等级,横向为PPA划分的等级,如第2行第3列的24代表SPI指数识别为I级、PPA指数识别为II级的样本数量为24。可见,对角线方向上样本数量越多,二者的一致性越高。根据式(3),总样本量n=14400,nα=(469+967+1270+1317+9925)=13948,nε=(525×529+1037×1051+1357×1410+1414×1479+10067×9931)/14400=7315.810,则Kappa系数κ=(13948-7315.810)/(14400-7315.810)=0.936。根据式(4)计算总体精度γ=13948/14400=0.969。由此可见,采用分位数方法的两指标的分类一致性非常好。 类似地,采用阈值分割法对两指标的等级划分结果进行一致性检验分析(SPI_T和PPA_T)。经计算,Kappa系数k=0.349,总体精度r=0.609。可见,阈值分割法两指标的一致性较差(k<0.4)。且从表 3所示的混淆矩阵可见,上三角区域的样本数较多,说明PPA指数比SPI指数普遍评估干旱偏重,这是指标的阈值设置所致。虽然通过修改PPA或SPI的阈值能够调整干旱等级划分的结果,提高二者的一致性,但这仍然是通过经验进行修改,缺乏物理和统计意义。 表2 SPI_P和PPA_P干旱等级划分混淆矩阵 表3 SPI_T和PPA_T干旱等级划分混淆矩阵 3.2 检验分析 上述一致性检验证明了分位数法比阈值分割法具有更好的一致性。实质上,通过分位数法进行干旱等级划分,得到的干旱等级阈值在不同时期(月份)是动态变化的,而阈值分割法的干旱等级阈值是固定不变的。表4所示是月尺度SPI(SPI_1)指数在不同月份对应5%、10%、20%和30%百分位数的数值,分别用于划分特旱-重旱、重旱-中旱、中旱-轻旱和轻旱-无旱。 可见,由分位数法得到的指标阈值存在明显的季节变化规律,在12、1和2月份冬季干燥少雨时期的阈值较大,在6、7、8月份湿润多雨时期的阈值较小。阈值分割法对应各干旱等级的阈值依次为-2.0、-1.5、-1.0和-0.5,普遍比表 4中分位数法的阈值小,这意味着阈值分割法的结果比分位数法评估的干旱等级偏轻。这一点可以从SPI指数的两种方法的一致性分析中得到验证(SPI_P和SPI_T),如表 5所示是对应的混淆矩阵,上三角区域的样本数较多,其中k=0.774 5,r=0.888。 表4 5%、10%、20%和30%百分位数的逐月SPI_1指数值 表5 SPI_P和SPI_T干旱等级划分混淆矩阵 与阈值分割法SPI指数轻估干旱相反,PPA指数的结果是干旱被重估,如表 6所示的PPA_P和PPA_T混淆矩阵,下三角区域的样本较多,其中k=0.446,r=0.685。 表6 PPA_P和PPA_T干旱等级划分混淆矩阵 表7 2001年平阴站各月干旱等级结果(月尺度) 注:标↓代表干旱被轻估,标↑代表干旱被重估。 为了更具体的体现分位数法和阈值分割法的差异,从所有样本数据中截取一小段进行分析。2001年是典型的干旱年,表 7所示是平阴站2001年月尺度SPI指数和PPA指数的干旱等级。分位数法下两种指数各月干旱等级完全一致;而阈值分割法下两种指数的干旱等级存在很大差异,3、4、8、9、10和11月份均不一致。如果以分位数法的结果为参照,阈值分割法的SPI_T有1个月轻估,PPA_T有6个月重估,如表 7中的箭头所示。这种结果的不一致对制定合理的抗旱减灾措施带来极大的困扰。 为了更清晰的阐述分位数法在多指标干旱评估一致性中的作用,对相关问题进一步讨论分析: (1)本研究之所以选择SPI指数和PPA指数进行分析,是因为它们都是基于月降雨量计算所得,物理机理一致,所判断的干旱等级应该具有高度的一致性。这也是本研究对这两种指标进行一致性分析的假设前提。 (2)虽然研究中利用分位数法只分析了SPI指数和PPA指数,但实质上,分位数法具有很好的“扩展性”,可以广泛应用于各种指标的等级划分。只要干旱指标的物理意义相同,通过分位数法得到的干旱等级就具有较高的一致性。反之,如果指标的物理意义不同,如前文所述的SPI和SWSI指数,则分位数方法恰好能体现不同类型干旱之间的差异。 (3)研究中利用大量的样本数据进行一致性检验,并主要借助混淆矩阵等统计工具进行分析。这是因为干旱等级划分的本质是将具体的定量值转化为直观的等级值,是一个由精细到概化的过程,通过单一或少量结果难以比较两种方法在干旱等级划分上的差异。因此,通过大量的样本数据,对每个样本(逐月的干旱等级结果)一对一的分析,并通过混淆矩阵的方式得出具有统计意义的结论。在此基础上,最终列出了表 7所示的一小段样本结果。 (4)干旱具有季节特性和区域特性,分位数法将当前状况与历史同期状况进行比较,给定统一的分位数阈值后,由此得到的各指标阈值是动态变化的,是一种“软”阈值。干旱的严重程度是跟自身的历史情况进行比较,不受人为主观因素影响,具有物理意义和统计意义。阈值分割法的指标阈值是固定不变的,是一种“硬”阈值。分位数法的不同指标之间通过分位数建立联系,将不同指标归一化到统一的标准体系下。阈值分割法对各个指标独立进行等级划分,不同指标之间对干旱严重程度的衡量缺乏统一的标准。 (5)分位数法的局限性在于:① 一般需要30年以上长序列的同期历史数据,否则,无法准确确定其分位值,进而无法划分干旱等级;② 对于气候条件或下垫面条件发生较大改变的不适用,因为历史状况发生改变影响分位值的准确确定;③ 对于受人类活动影响较大的指标不适用,如水库蓄水受人为调解影响较大,基于水库蓄水量的干旱指标不适宜采用分位数法。 随着干旱监测技术的不断完善,利用多指标的综合干旱监测能够更全面、客观的反映干旱的严重程度,成为当前干旱评估的主要方法手段。然而传统的阈值分割法划分干旱等级采用的是统一的阈值,导致不同指标得到的干旱等级存在不一致性,对抗旱决策的制定帮助不大。本研究提出分位数法直接用于干旱等级划分的思想,即通过指标值在长历史序列中的百分位数确定干旱等级。研究以SPI指数和PPA指数为例,采用分位数法与阈值分割法分别进行干旱等级划分,通过对结果的一致性检验和深入分析表明:① 不同指标采用分位数法进行等级划分,得到的结果具有较高的一致性;② 分位数法能够广泛应用于各种干旱指标的等级划分;③ 分位数法划分干旱等级考虑了干旱的季节特性和区域特性,具有物理和统计意义。利用分位数法进行干旱等级划分,能够解决多指标干旱监测结果矛盾的问题,实现多干旱指标的综合统一,为制定合理的抗旱减灾措施提供科学准确的依据。 [1] Wilhite D A. Drought as a natrural hazard: concepts and definitions [M]. Drought : a global assessment, D.A. Wilhite, Editor. Routledge: London & New York, 2000: 3-8. [2] Mishra A K, Singh V P. A review of drought concepts [J]. Journal of Hydrology, 2010, 391(1/2): 202-216. [3] Bärring L, Hulme M. Filters and approximate confidence intervals for interpreting rainfall anomaly indices [J]. Journal of Climate, 1991, 4(4): 837-847. [4] McKee T B, Doesken N J, Kleist J. The relationship of drought frequency and duration to time scales [C]//Proceeding of 8th Conference on Applied Climatology. Boston: American Meteorological Soeiet, 1993. [5] 韩海涛, 胡文超, 陈学君, 等. 三种气象干旱指标的应用比较研究 [J]. 干旱地区农业研究, 2009, 27(1): 237-241. [6] Guttman N B. Comparing the palmer drought index and the standardized precipitation index [J]. Journal of the American Water Resources Association, 1998, 34(1): 113-121. [7] Shafer B, Dezman L. Development of a Surface Water Supply Index (SWSI) to assess the severity of drought conditions in snowpack runoff areas [C]//Proceedings of the Western Snow Conference, 1982. [8] Palmer W C. Keeping track of crop moisture conditions, nationwide: The new crop moisture index [J]. Weatherwise, 1968, 21(4): 156-161. [9] Liu W, Kogan F. Monitoring regional drought using the vegetation condition index [J]. International Journal of Remote Sensing, 1996, 17(14): 2761-2782. [10]Wilhite D A. Drought planning: A process for state government [J]. Water Resources Bulletin, 1991, 27(1): 19-38. [11]Richard R, Heim J. A review of twentieth-century drought indices used in the United States [J]. Bulletin of the American Meteorological Society, 2002, 83(8): 1149-1165. [12]Keyantash J, Dracup J A. The quantification of drought: An evaluation of drought indices [J]. Bulletin of the American Meteorological Society, 2002, 83(8): 1167-1180. [13]宋超辉. 分位值的统计及其应用 [J]. 气象, 1983(12): 23-24. [14]Svoboda M, LeComte D, Hayes M, et al. The drought monitor [J]. Bulletin of the American Meteorological Society, 2002, 83(8): 1181-1190. [15]Karavitis C A, Alexandris S, Tsesmelis D E, et al. Application of the Standardized Precipitation Index (SPI) in Greece [J]. Water, 2011, 3(3): 787-805. [16]Carletta J. Assessing agreement on classification tasks: the kappa statistic [J]. Computational linguistics, 1996, 22(2): 249-254. [17]Stehman S V. Selecting and interpreting measures of thematic classification accuracy [J]. Remote Sensing of Environment, 1997, 62(1): 77-89. [18]Fleiss J L. Statistical methods for rates and proportions (2nd ed.) [M]. New York: John Wiley, 1981. [19]GB/T 20481-2006 气象干旱等级 [S]. 北京:中国标准出版社, 2006. [20]GB/T 32135-2015 区域旱情等级 [S]. 北京:中国标准出版社, 2015. TheEffectivenessoftheQuantileMethodontheConsistencyoftheDroughtClassificationbyMultipleIndices SUN Hongquan1, 2, LV Juan1, 2, SU Zhicheng1, 2, SONG Sulin3and Wang Yaxu1, 2 (1.ChinaInstituteofWaterResourcesandHydropowerResearch,Beijing100038,China; 2.ResearchCenteronFloodandDroughtDisasterReductionofMinistryofWaterResources,Beijing10003,China; 3.JinanHydrologyBureau,Jinan250099,China) Inordertoassesstheseverityofdroughtaccuratelyandcarryingoutreasonabledroughtmitigationcountermeasures,avarietyofdroughtindicatorsareusuallyusedtoassessthedrought.However,theresultsderivedfromdifferentindicatorsareofteninconsistent.Forexample,anindexidentifiedasmilddrought,whileanotherindexindicatedasextremedrought.Themainreasonisthatthethresholdsoftheindicatorsarenotreasonable.Thetraditionalthresholdsegmentationmethodhasagreatinfluenceontheclassificationofdroughtlevel,whichisshortofuniformstandards.Weputforwardanideaofdroughtclassificationusingthequantilemethod.Inthestudy,thethresholdsegmentationmethodandquantilemethodareimplementedtoclassifythedroughtseveritiesforStandardPrecipitationIndex(SPI)andthePercentageofPrecipitationAnomalyindex(PPA),respectively.Thentheconsistencyofthedroughtlevelsarecomparedandanalyzed.Theresultsshowthat: 1)thedroughtlevelsofdifferentindicesusingquantilemethodshavehighconsistency; 2)Quantilemethodhaswideapplicability,whichcanbeusedfortheclassificationofavarietyofindices; 3)Thethresholddeterminedbyquantilemethodaredynamicchangedwiththeseasonalandregionalcharacteristicsofdrought,whichisfullofphysicalinterpretationandstatisticalsignificance. quantile;droughtclassification;multipleindicators;thresholdsegmentation;consistency;standardprecipitationindex;percentageofprecipitationanomalies 2016-08-24 2016-10-12 国家自然科学基金项目(51209220);中国水利水电科学研究院科研专项 (1402, JZ0145B592016);水利部公益性行业科研专项(201401036) 孙洪泉(1983-), 男, 辽宁丹东人, 高级工程师, 主要从事干旱监测研究. E-mail:sunhq@iwhr.com 苏志诚(1974-),男,河北衡水人,教授级高级工程师,主要从事抗旱减灾研究. E-mail:suzhc@iwhr.com 10.3969/j.issn.1000-811X.2017.02.003.] X43;P467;S27 A 1000-811X(2017)02-0013-06 10.3969/j.issn.1000-811X.2017.02.003 孙洪泉,吕娟,苏志诚,等. 分位数法对多指标干旱等级划分一致性的作用[J]. 灾害学,2017,32(2):13-17,53. [SUN Hongquan, LV Juan, SU Zhicheng,et al. The Effectiveness of the Quantile Method on the Consistency of the Drought Classification by Multiple Indices[J]. Journal of Catastrophology,2017,32(2):13-17,53.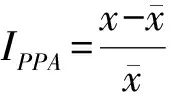
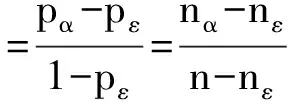
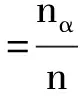
2 数据与等级划分
3 结果与讨论

4 讨论
5 总结

