城市轨道交通列车运行图能力与客流需求匹配度的评价方法
李思杰,徐瑞华,江志彬
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.同济大学 交通运输工程学院,上海 201804)
列车运行图是城市轨道交通运输工作的生产计划,其编制质量的高低直接影响运输组织的效率和服务水平。网络化运营条件下,客流需求分布呈现时空维度的差异性,如何权衡运营成本与服务质量,编制以需求为导向的列车运行图,是运营管理部门亟须解决的问题之一。要实现上述目标,首先需要判断客流需求与运行图能力的匹配程度,仅仅靠宏观总量比较需求程度与运能供给量匹配的方法难以得到理想的评价结果。因此,有必要考虑客流需求的时空分布特征,提出运行图能力匹配性的定量评价方法,用以衡量运行图能力配置的合理程度,为有效改善运行图编制质量提供决策依据。
目前,对列车运行图性能的评估有不同的标准。对于运行图的生产效益,运营企业常用列车开行对数、车底运用总数、列车旅行速度、能量消耗总量等成本类的指标[1-2]进行衡量;对于运行图的服务质量,大多数学者针对运行图受到随机因素扰动的情况下,利用列车正点率、平均晚点时间、总延误时间、晚点恢复率等与延误相关的指标对运行图的稳定性[3-5]、鲁棒性[6-7]、可靠性[8-9]等进行评价,这些研究成果都重点关注列车的运行过程。而作为公共交通的重要组成部分,城市轨道交通应该提供以用户为中心的交通服务,满足客流需求应该是衡量运行图性能的另一重要标准,但这方面的研究成果较少。Kunimatsu[10]等考虑候车时间、换乘次数和列车拥挤度计算乘客负效用,从乘客的角度评价列车运行图;Jiang[11]基于微观仿真得到列车满载率、留乘人数、乘客额外等待时间等指标分析运行图的能力利用情况,但没有给出总体的评价结果。综上所述,以往的评价指标主要针对列车运行图单方面的性能,很少同时考虑不均衡客流的分布特征和列车能力限制,结合乘客利益与企业利益对运行图能力配置的合理程度进行综合评价。
本文基于实际客流数据,从微观到宏观定量评价客流需求与城市轨道交通列车运行图能力的匹配度。在微观上,构建客流与列车的交互模型,得到列车载客量、满载率、留乘人数、平均候车时间等微观指标;在宏观上,提出运行图能力匹配度的概念及其计算方法,从乘客角度和企业角度对运行图能力与乘客需求的匹配性进行综合评价;并以上海轨道交通为例进行实证分析,验证本方法的可行性和合理性。
1 客流与列车的交互模型
为了从微观层面揭示城市轨道交通列车与客流的动态影响机理,基于实际客流数据,构建客流与列车的交互模型,并设计可视化工具,展示运行图能力与客流需求在时空分布结构上的匹配关系。
1.1 输入数据
本模型需要输入以下3类数据。
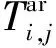
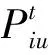
(3)列车编成辆数为C;车辆定员数为Q;列车能够承载的最大载客比率为k。
1.2 输出指标
本模型将输出4类指标:每班列车对应每个区间的载客量、满载率;每趟列车离开后车站的留乘人数;乘客的平均候车时间。这4类指标可以详细描述客流与列车交互作用的结果。
1)列车载客量
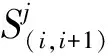
(1)
则j列车载客量的计算公式为
(2)
2)列车满载率
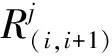
(3)
3)留乘人数
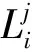
(4)
4)平均候车时间
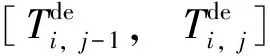
(5)
在实际情况中,高峰时段客流量较大,受列车容量限制会出现乘客滞留现象,从而造成留乘乘客额外的等待时间Γ″,即
(6)
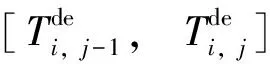
(7)
式中:β为留乘惩罚系数。
1.3 客流与列车动态匹配的交互算法
客流与列车动态匹配的交互算法是在考虑列车容量约束的基础上,在研究时段[tbegin,tend]内,从第1个车站经过的第1班列车开始,对每一班列车依次经过沿线每一个车站进行循环,计算列车到达车站的上、下车人数,实现所有列车与客流的动态匹配,最终输出评价所需的4类微观指标。具体的算法流程如下。
步骤1:输入列车时刻表,OD客流数据,列车编成辆数C,车辆定员数Q,列车能够承载的最大载客比率k。
步骤2:运算初始化。令i=1,j=1。
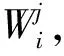
(8)
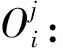
(9)

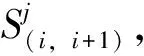
步骤6:i=i+1。若i 步骤7:j=j+1。若j≤N,令i=1,转步骤3,继续计算下一列车j+1在所有区间的载客情况;否则,转步骤8。 步骤8:所有列车计算完毕,输出4类指标,算法终止。 为了直观展示实际客流与列车在时空维度的动态作用结果,基于信息可视化理论,构建描述列车载客量、满载率、留乘人数的可视化模型[12-14]。本文在普通列车运行图的基础上,结合热力图的原理,将列车满载率和留乘人数的取值离散为多组,每一组对应1种颜色,构造1种色阶运行图,实现对列车运行计划执行效果的可视化。在构造的色阶列车运行图中,列车运行线被赋予宽度和颜色,分别表示列车所在区间的载客量和满载率,列车之间的圆圈表示前一趟列车离开后的车站留乘人数。色阶运行图以图形方式描述了每趟列车在每个区间的能力利用情况,直观反映出能力紧张与能力富余的区段,为运行图的优化提供决策支持。此外,基于人机交互理论,能够实现不同满载率的列车运行区段的筛选,以辅助运营人员查看需要重点关注的区段。 为了全面反映列车运行图的性能,综合所有区间和车站的微观指标,进一步从宏观层面对运行图能力与客流需求的匹配度进行综合评价。 城市轨道交通列车运行图能力与乘客需求相匹配是指运能供给既能够充分满足乘客需求又能够使自身的能力得到高效的利用。企业作为能力供给方,希望通过运行图获取高的经济效益,即每一趟列车能够尽可能运送更多的乘客,但这会对服务质量造成影响。而乘客作为需求方,希望运行图的服务质量处于较高的水平,即列车的拥挤度和候车时间控制在舒适的范围内,但这又会牺牲企业效益。可见,企业利益和乘客利益呈对立相关, 只有合理权衡二者的关系,运行图能力供给与客流需求才能达到匹配状态。因此,本文提出运行图能力匹配度的概念,指运行图计划运输能力与实际客流需求之间的吻合程度,用以综合衡量运能供给对于乘客需求和企业需求两方面的匹配关系,是反映运行图能力配置合理程度的综合性评价指标。 兼顾满足运能供给方和需求方的利益,运行图能力匹配度取决于乘客满意度和企业满意度两方面,其中乘客满意度由乘车舒适度和候车满意度两要素所决定,因此以三者的合成值作为匹配度的评价结果。目前决策科学中常用的多目标合成模型有加法合成和乘法合成。加法合成认为指标间可以相互替代,较好指标的优势可以弥补较差指标的不足;而乘法合成强调指标全面发展,因为若某项指标偏低就会导致总体评价值降低[15-16]。鉴于此,本文采用乘法合成法计算列车运行图的能力匹配度Kmatch,其函数表达式为 Kmatch=Xγ1Yγ2Zγ3 (10) 式中:X为乘车舒适度;Y为候车满意度;Z为企业满意度;γ1,γ2,γ3为权重系数,可利用专家打分法确定,且γ1+γ2+γ3=1。 在交互模型所得微观指标的基础上对匹配度的三类影响要素进行量化。由于微观指标的量纲单位不同,采用梯度分布函数对其做无量纲化处理[17],正向指标采用“升半梯形分布”,逆向指标采用“降半梯形分布”,函数形态如图1所示。然后,对所有评价单元进行加权平均得到影响要素的评价值。 图1 梯度分布函数图 1)乘车舒适度 列车运行图的乘车舒适度X主要取决于每班列车经过每个区间的载客量S。当载客量小于座位数时,乘客都有座位,舒适度为1;当乘客站立时,舒适度随车内密度的增加而减小;当载客量超过列车额定容量时,车内过度拥挤,舒适度为0。每班列车的乘车舒适度采用“降半梯形分布”函数确定,即 (11) 式中:Sa为列车的座位数,Sb为列车的额定载客量。 研究时段内列车运行图的乘车舒适度X为所有评价单元乘车舒适度的平均值,即 (12) 式中:A为研究时段内所有评价单元的总数。 2)候车满意度 列车运行图的候车满意度Y以乘客平均候车时间Γ的长短来衡量。当候车时间在理想候车时间范围内时,则满意度为1;随着候车时间的增加,乘客满意度降低;当候车时间超出乘客容忍的最大候车时间时,乘客就会产生不满,候车满意度为0。每班列车的候车满意度采用“降半梯形分布”函数确定,即 (13) 式中:Γa为乘客的理想候车时间;Γb为乘客能够接受的最长候车时间。 研究时段内列车运行图的候车满意度Y为 (14) 3)企业满意度 列车运行图的企业满意度Z通过列车的满载率R表征。满载率越高,企业的满意度越好;当满载率过低时,说明运能严重浪费,企业满意度为0。每班列车的企业满意度采用“升半梯形分布”函数确定,即 (15) 式中:Ra为企业能够接受的最低满载率;Rb为企业期望的列车满载率。 研究时段内列车运行图的企业满意度Z为 (16) 以上海轨道交通9号线工作日的列车运行图为例进行实证分析。9号线工作日列车运行图:客流早高峰时间段为07:00—09:00,晚高峰时间段为17:00—19:00;在高峰时间段采用1∶1的大小交路运输组织方式,大交路为松江南站—杨高中路站,小交路为佘山站—杨高中路站;其他时段为单一交路。列车编组为6辆A型车,车辆定员为310人·车-1。采用2016-03-07(星期一)的OD客流数据,对列车运行图的能力匹配度进行分析及评价。根据9号线的实际情况设定:列车最大载客率k=130%;留乘惩罚系数β=2;权重系数γ1=30%,γ2=30%,γ3=40%;列车的座位数Sa=288个,列车额定载客量Sb=1 860人;乘客理想候车时间Γa=2 min,乘客接受的最长候车时间Γb=5 min;企业接受的最低满载率Ra=20%,企业期望满载率Rb=100%。 以上行方向(松江南站至杨高中路站)为例,利用本文提出的客流与列车交互模型将实际客流数据与列车运行图进行精确匹配,所得可视化结果如图2所示。 图2 上海地铁9号线色阶列车运行图 图2展现了客流的时空分布特征以及每班列车在每个区间的载客情况,能够直观地识别列车运行图中的关键区间和关键车站。由图2可以看出:在8:00—9:00时间段从九亭站到徐家汇站显示为红色和深红色,说明此时该段为拥挤区段,尤其是在8:20—9:00时间段,七宝站至漕河泾开发区站的3个区间为深红色,即列车满载率大于120%,说明此时列车严重拥挤,运能供应远不能满足客流需求,这是因为9号线上行方向是从郊区到市区,早高峰期间通勤客流量大,能力供给与客流需求的矛盾突出;而同样在8:00—9:00时间段,世纪大道站至杨高中路站、松江南站至松江大学城站之间的列车满载率小于20%,说明运能供应远大于客流需求;图2中的圆圈表示七宝站、星中路站和合川路站在8:20—9:00时间段内持续有留乘人数,并且在8:40留乘人数逐渐增加至最大值,然后逐渐减小,直至消散,因此建议在客流早高峰期间对这3个车站加强客运组织力度,预防大客流风险。 根据客流的时间分布特征,将列车运行图分为运营开始、早高峰、平峰、晚高峰和运营结束5个时段,分别对其能力匹配度进行评价,结果见表1。由表1可知:从乘车舒适度来看,运营开始和结束时段的最好,平峰时段次之,早高峰时段由于列车严重超载导致其最低;从候车满意度来看,高峰时段的候车满意度高于其他时段,早高峰由于留乘现象严重导致其候车满意度低于晚高峰,运营开始和结束时段的发车间隔较大,所以乘客候车满意度最低;从企业满意度来看,由于早高峰的客流量最大因而其企业满意度最好,而平峰、开始和结束时段的企业满意度都较低,说明运能浪费严重。 表1 分时段指标统计 能力匹配度是以上3方面的综合评价,由表2可知:晚高峰时段的能力匹配度最高,说明能力利用最为均衡,早高峰和平峰时段的次之,运营开始和结束时段的匹配度最低。可见,单方面的优势并不能弥补其他方面的不足,只有乘车舒适度、候车满意度和企业满意度都达到较好的水平,整体的能力匹配度才得以最优,这也符合实际情况。 为了适应动态多变的客流需求,需要相应地调整运力资源配置。在列车编组、交路已定的条件下,列车发车频率设计是协调客流需求与运能供给的最佳手段,能力匹配度可以有效地衡量发车频率的优化效果。选取早高峰时段8:00—9:00和平峰时段13:00—14:00,在目前列车运行图(早高峰发车频率20列/小时,平峰11列/小时)的基础上,分别增加和减少列车发车频率,分析其对能力匹配度的影响,如图3所示。 图3早高峰时段不同列车发车频率时不同指标的变化曲线 从图3可以看出:在早高峰时段,随着列车发车频率的增加,乘车舒适度和候车满意度呈上升趋势,说明列车数量的增加很好地缓解了乘客滞留现象并降低了列车的拥挤度,服务水平得到提高;但企业满意度随之降低,因为客流需求不变的条件下增加运能供给,导致列车的满载率降低;能力匹配度呈先增后减的趋势,当列车发车频率增加为23列时,匹配度达到最高,为61.63%。 图4 平峰时段不同列车发车频率时不同指标的变化曲线 从图4可以看出:在平峰时段,随着列车发车频率的减少,列车发车间隔随之增加,导致乘车舒适度和候车满意度不断降低,而企业满意度得到明显提升;当列车发车频率减少至8列车时,匹配度达到最高,为52.31%,随后不断降低。 可见,企业满意度和乘客满意度是相互矛盾的,列车运行图的优化是服务水平和运营效益不断权衡的过程。本文以能力匹配度指标为参考,建议上行早高峰期间增加列车发车频率为23列/小时,以提高运营服务水平,平峰时段减少列车发车频率至8列/小时,从而达到节省企业运营成本,提高列车运行图对客流分布不均衡的适应性,实现企业和乘客的综合利益最大化。 (1)为了衡量列车运行图能力配置与不均衡客流需求的匹配性,提出能力匹配度的概念,并给出基于实际客流数据计算匹配度的方法。 (2)考虑列车能力约束,构建列车与客流的交互模型,输出列车经过每个区间的载客量、满载率、留乘人数、平均候车时间等4类指标,描述运能供需的微观机制,并利用色阶列车运行图从时空维度展示客流与列车的动态作用结果。 (3)在上述微观指标的基础上,采用梯形分布函数量化匹配度的3个影响因素:乘车舒适度、候车满意度和企业满意度,并采用乘法合成模型计算能力匹配度,对列车运行图能力与客流需求的匹配度进行综合评价。 (4)以上海轨道交通9号线的实际客流数据进行实例分析的结果表明:该线上行方向8:00—9:00能力供给与客流需求的矛盾突出,与实际运行状况一致;该线上行方向晚高峰时段的匹配度最高,早高峰和平峰时段的次之,运营开始和结束时段的最低,说明能力匹配度反映了各指标的均衡性,有效评价了企业与乘客的综合利益;分别增加高峰时段和减少平峰时段的列车发车频率,能力匹配度呈先上升后下降的趋势,说明能力匹配度能够为调整运能配置提供明确的方向。本文提出的方法能够对城市轨道交通列车运行图能力与客流需求的匹配程度进行合理有效的分析与评价。 [1]蒲松, 吕红霞, 陈钉均, 等. 基于改进列生成算法的高速列车开行方案优化研究[J]. 铁道学报, 2015, 37 (9): 1-7. (PU Song, LÜ Hongxia, CHEN Dingjun, et al. High Speed Railway Passenger Train Line Planning Optimization Based on Improved Column Generation Algorithm[J]. Journal of the China Railway Society, 2015, 37(9): 1-7. in Chinese) [2]LI Xiang, LO H K. Energy Minimization in Dynamic Train Scheduling and Control for Metro Rail Operations[J]. Transportation Research Part B: Methodological, 2014, 70: 269-284. [3]马驷, 邓云霞. 城际铁路列车运行图稳定性仿真分析[J]. 中国铁道科学, 2016, 37(2): 122-127. (MA Si, DENG Yunxia. Simulation Analysis on Stability of Train Working Diagram for Intercity Railway[J]. China Railway Science, 2016, 37(2): 122-127. in Chinese) [4]DELORME X, GANDIBLEUX X, RODRIGUEZ J. Stability Evaluation of a Railway Timetable at Station Level[J]. European Journal of Operational Research, 2009, 195 (3): 780-790. [5]GOVERDE R M P. Railway Timetable Stability Analysis Using Max-Plus System Theory[J]. Transportation Research Part B: Methodological, 2007, 41 (2): 179-201. [6]NICHOLSON G L, KIRKWOOD D, ROBERTS C, et al. Benchmarking and Evaluation of Railway Operations Performance[J]. Journal of Rail Transport Planning and Management, 2015, 5(4): 274-293. [7]OCHIAI Y, TOMII N. Punctuality Analysis Using a Microscopic Simulation in Which Drivers’ Behaviour is Considered[J]. Journal of Rail Transport Planning and Management, 2015, 5 (3): 128-145. [8]孟令云, 杨肇夏, 李海鹰, 等. 基于列车运行线分布的客运专线列车运行图动态性能分析[J]. 中国铁道科学, 2010, 31(2): 90-95. (MENG Lingyun, YANG Zhaoxia, LI Haiying, et al. Analysis on the Dynamic Performance of PDL Train Working Diagram Based on Train Path Layout[J]. China Railway Science, 2010, 31(2): 90-95. in Chinese) [9]VROMANS M J C M, DEKKER R, KROON L G. Reliability and Heterogeneity of Railway Services[J]. European Journal of Operational Research, 2006, 172(2): 647-665. [10]KUNIMATSU T, HIRAI C, TOMII N. Train Timetable Evaluation from the Viewpoint of Passengers by Microsimulation of Train Operation and Passenger Flow[J]. Electrical Engineering in Japan, 2012, 181(4): 51-62. [11]JIANG Zhibin, HSU C H, ZHANG Daqiang, et al. Evaluating Rail Transit Timetable Using Big Passengers’ Data[J]. Journal of Computer and System Sciences, 2015, 82 (1): 144-155. [12]HU P S, PACK M L. Visualization & Visual Analytics in Transportation[J]. Transportation Research Part C: Emerging Technologies, 2014, 47: 193. [13]YAMAMURA A, KORESAWA M, ADACHI S, et al. Taking Effective Delay Reduction Measures and Using Delay Elements as Indices for Tokyo’s Metropolitan Railways[J]. Computers in Railways XIV, 2014, 135: 3-15. [14]HRANAC R, KWON J, BACHMANN M, et al. Using Marey Graphs to Visualize Transit Loading and Schedule Adherence[C]// Transportation Research Board 90th Annual Meeting. Washington: Transportation Research Board, 2011: 11-0350. [15]苏为华. 多指标综合评价理论与方法问题研究[D]. 厦门: 厦门大学, 2000. (SU Weihua. Research on Theory and Method of Multiple Objective Comprehensive Evaluation[D]. Xiamen: Xiamen University, 2000. in Chinese) [16]商红岩, 宁宣熙. 基于乘法合成的层次分析模型的第三方物流企业绩效评价[J]. 科技进步与对策, 2005, 22(11): 94-96. (SHANG Hongyan, NING Xuanxi. The Performance Evaluation of 3PL Enterprises Based on the AHP Model of Multiplicative Synthesis[J]. Science and Technology Progress and Policy, 2005, 22(11): 94-96. in Chinese) [17]楼世博. 模糊数学[M]. 北京: 科学出版社, 1983. (LOU Shibo. Fuzzy Mathematics[M]. Beijing: Science Press, 1983. in Chinese)1.4 结果可视化
2 能力匹配度评价
2.1 能力匹配度的定义
2.2 运行图能力匹配度影响要素计算
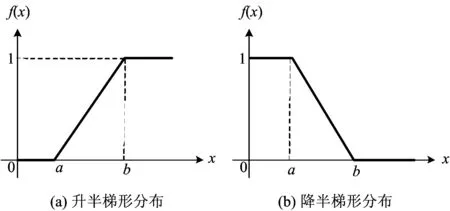
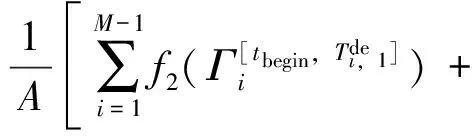
3 实证分析
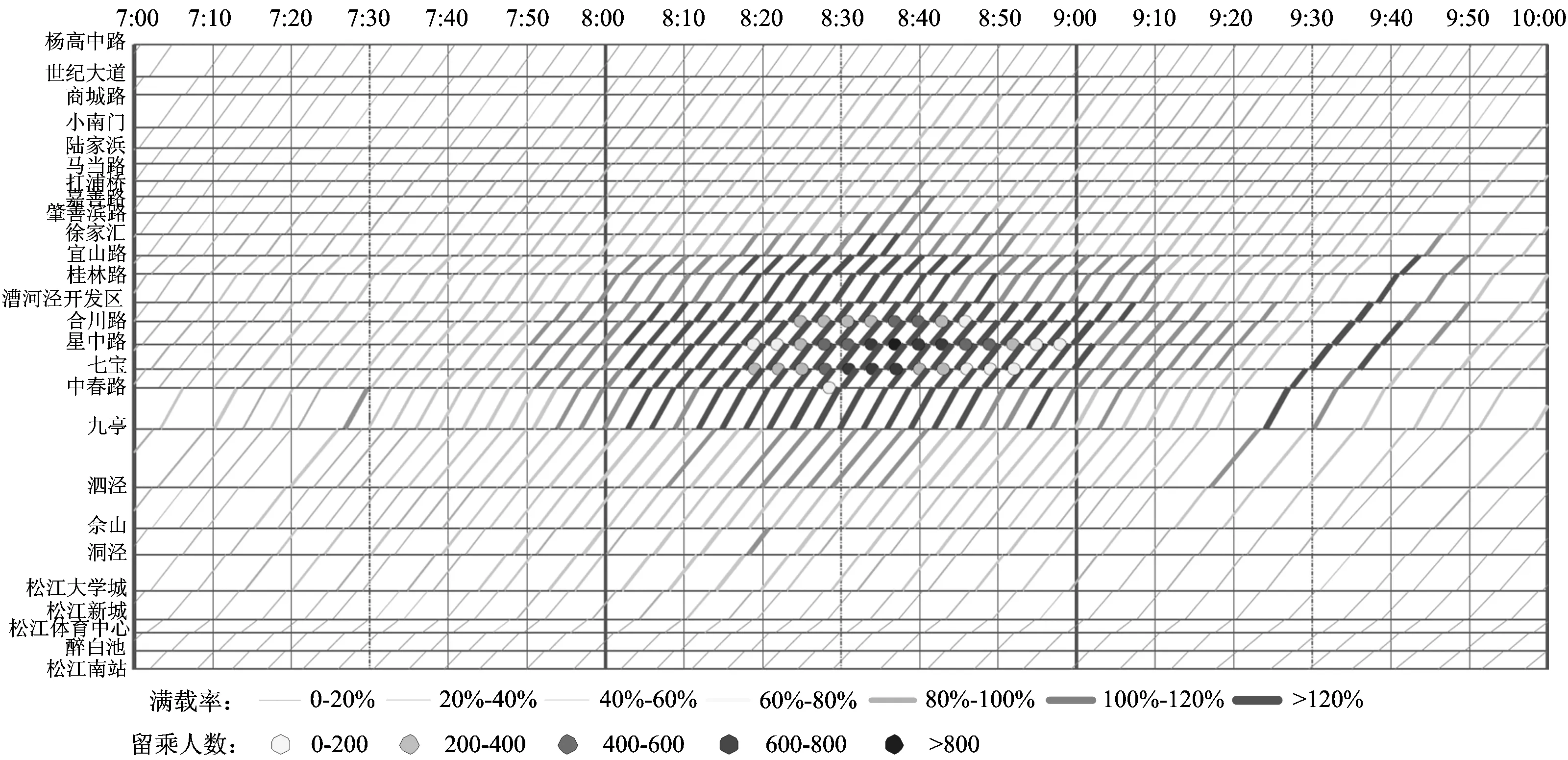
3.1 可视化分析
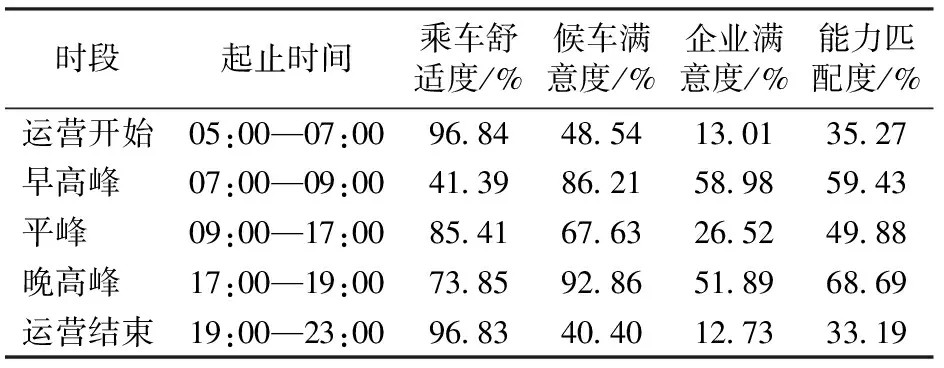
3.2 分时匹配度评价
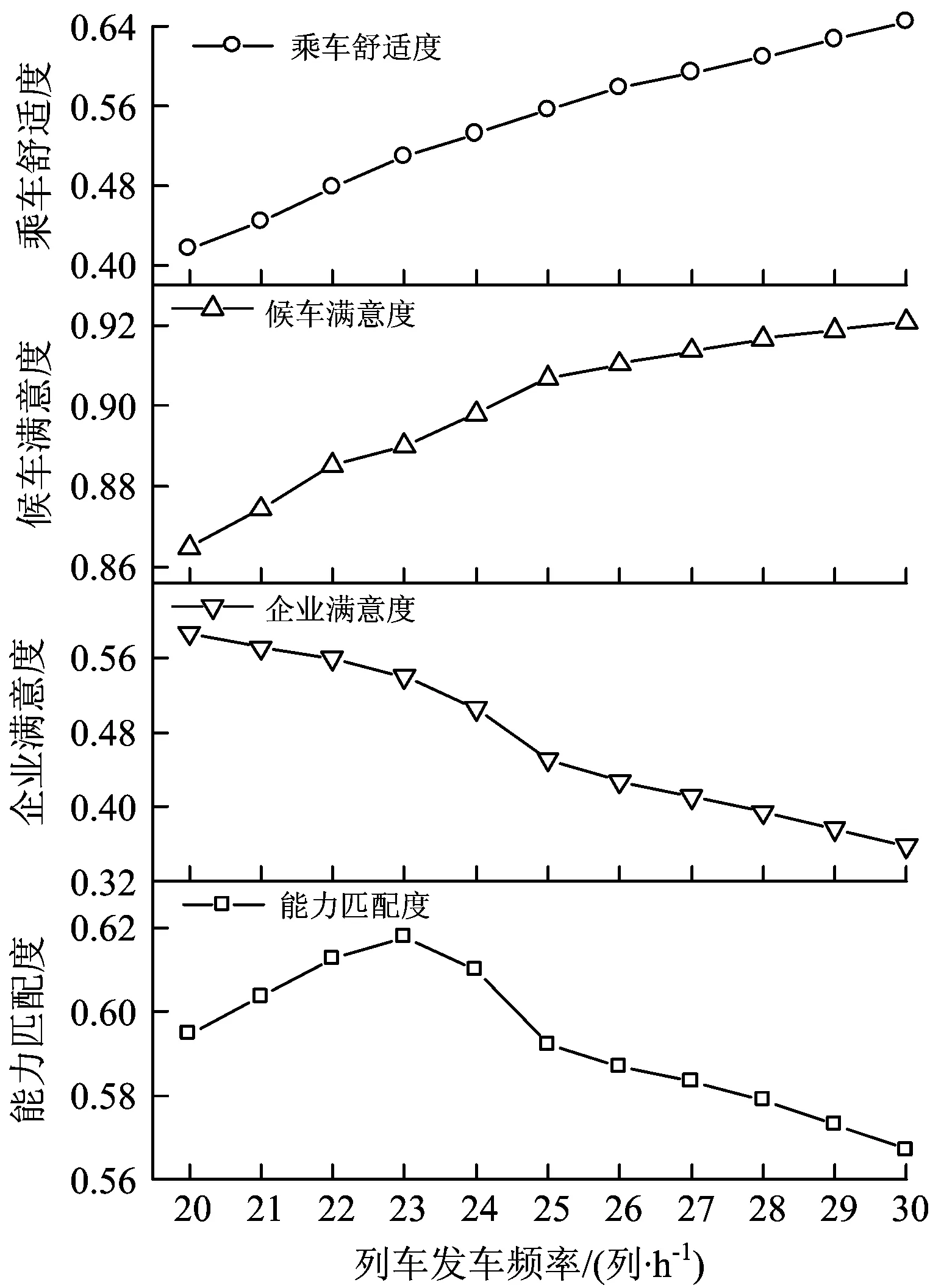
3.3 不同列车发车频率时能力匹配度的评价
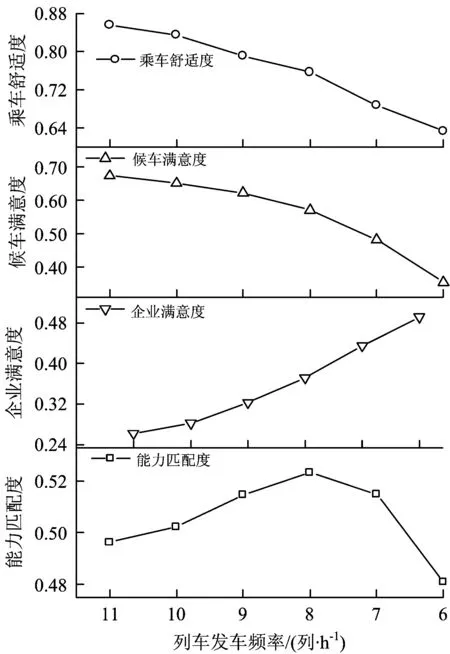
4 结 语

