飞秒激光烧蚀血管支架材料的数值模拟

王雷雷，郑洋洋，霍 扬，刘建英，李春霞，卢 洋

(山东理工大学机械工程学院，山东 淄博 255049)



飞秒激光烧蚀血管支架材料的数值模拟

王雷雷，郑洋洋，霍 扬，刘建英，李春霞，卢 洋

(山东理工大学机械工程学院，山东 淄博 255049)

王雷雷

为了研究飞秒脉冲激光烧蚀血管支架材料的特性，利用考虑了电子之间热传导项的双温模型，采用有限差分法，对飞秒激光烧蚀NiTi合金的温度场分布进行数值模拟，计算得到了电子温度和晶格温度随时间和烧蚀深度的变化规律，进一步讨论了不同激光能量密度、不同激光脉宽、不同延迟时间对电子和晶格的温度场影响。发现血管支架材料在飞秒激光的作用下，先是电子吸收能量温度快速升高，再通过电声耦合作用将能量传递给晶格，最后两者的温度达到一个平衡状态；激光能量密度主要影响电子的峰值温度和电子与晶格的平衡温度；脉冲宽度主要影响电子的峰值温度和达到峰值温度所用的时间；电子温度随着延迟时间的增加先升高后降低，晶格温度随着延迟时间的增加不断上升。这些理论分析对实际飞秒激光加工血管支架有重要的指导意义。

飞秒激光；镍钛合金；血管支架；双温方程；电子温度；晶格温度

1 前 言

NiTi合金材料是形状记忆金属中最重要且应用最为广泛的合金，具有优异的形状记忆效应和超弹性、良好的耐疲劳性能和抗腐蚀性，较强的生物相容性，因此成为一种较为理想的生物工程材料，在现代医学介入医疗器械领域得到了广泛应用[1-3]。其中NiTi合金血管支架的研究和制备具有重要的应用价值，它的基本原理是支架植入血管后，依靠材料的形状记忆功能自动恢复形状，把狭窄血管撑开，恢复远端血管供血，在大规模的实际临床应用中取得了很好的治疗效果[4]，具有取代传统不锈钢血管支架的趋势。由于支架的尺寸微小，一般尺寸小于100 μm，如果采用普通的机械加工方法，很难满足其加工要求；光纤激光器等普通的激光加工会对支架产生热影响区和重铸层[5]，需要电化学抛光等后续处理，给加工工艺带来了一定难度；而飞秒激光加工具有热影响范围小、切缝周围粗糙度小、切口平行度好、定位精度高、工件的形变小、无机械应力等特点，可精确切割形状复杂的特殊微细零件[6,7]，因此利用飞秒激光加工NiTi合金的血管支架具有独特的优势。目前对飞秒激光与金属作用的理论研究主要集中在铜、铝、金等材料，实验研究主要有打孔、划线、表面周期结构等。关于飞秒激光用于血管支架加工的研究主要有：新加坡的Bryan和德国汉诺威激光中心的Ostendorf利用飞秒激光加工出的血管支架得到了相关学者的瞩目[8]；程萍等人利用飞秒激光加工了以聚乳酸为材料的可降解血管支架，证明了飞秒激光在此方面的优势[9]；而国内关于利用飞秒激光加工金属材料血管支架的研究却很少，并且飞秒激光与金属材料的作用过程受到激光器的选取参数、加工工艺环境和材料的特性等众多因素的影响，其内在加工的机理也比较复杂，目前还没有统一的定论来解释飞秒激光与材料的相互作用。因此为了高效利用飞秒激光，使其在加工血管支架时达到更理想的实际效果，有必要从微观角度理论分析飞秒激光加工工艺参数对靶材内部的温度影响规律。

从双温方程入手，采用有限差分法，以NiTi合金为例，模拟了飞秒激光烧蚀血管支架材料的温度场分布情况；同时探究了不同参数对电子和晶格温度的影响规律。

2 计算模型

2.1 双温方程

前苏联学者Anisimov S I根据飞秒激光对金属作用的特殊机理，在1974年提出了适用于飞秒激光和金属作用的双温模型[10]。它是用来阐述飞秒激光和金属材料相互作用的数学模型，考虑分析了烧蚀过程中光子和电子、电子之间、电子和晶格之间以及晶格之间的一系列相互作用[11]，考虑了整个过程中的能量平衡，列出了电子和晶格温度变化的微分方程，其表达式为：

(1)

(2)

式中C表示热容，T表示温度，下角标e和i分别代表电子和晶格系统。方程(1)右边第一项为电子的热传导项，ke为电子的热传导率；第二项为电子和晶格的能量耦合，g为电子晶格耦合系数；第三项S为激光热源。方程(2)的右边代表作用过程中电子和晶格的能量耦合，因为晶格和晶格的耦合作用极小，可以忽略，所以对于晶格而言只与电子有能量的传递。由方程(1)和(2)可以看出，超短激光脉冲烧蚀金属材料时，首先是电子吸收激光光子的能量，然后通过电子与晶格之间的耦合作用，使晶格温度升高，产生烧蚀，达到精细加工目的。

很多学者在研究双温方程时，经常会忽略电子之间的热传导项或者把电子的热传导率看作一个常数，而实际上当飞秒激光照射到金属靶材表面时，电子将被加热到很高的温度，甚至接近或超过费米温度。此时电子热传导率的表达式应为[12]：

(3)

式中μe=Te/TF,μi=Ti/TF，NiTi合金的费米温度TF=8.12×104K,参数χ和η是和被加工材料相关的参数，分别为336 W·K-1·m-1和0.178。

飞秒激光的光源为高斯光束，因此光源项S(x,t)的表达式为[13]：

(4)

式中A代表消光系数，α为材料的吸收系数，F为激光的能量密度，τL为激光的脉冲宽度，x为距材料表面的轴向距离。

2.2 计算方法

对双温方程的数值求解采用有限差分法，差分采用时间向前空间中心差分法(FTCS)全隐格式，迭代法求解[14]。Δt和Δx分别为时间步长和轴向步长，i和j分别为轴向步数和时间步数，由此得双温模型的差分表达式为式(6)和式(7)：

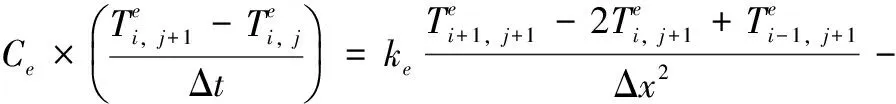
(6)

(7)

(8)

(9)

exp(-αiΔx)

初始条件和边界条件满足：

Ti,0=T0=300K,(i=1,2,3,…,n)

Tn,j=300K,(j=0,1,2,…,m)

2.3 采用参数

模拟采用的飞秒激光器是美国Raytum Corp生产的二极管直接泵浦超快激光器。其参数为：激光能量，F=100 J/m2；脉宽，τL=300 fs；波长为1030 nm。

取时间差分步长0.1 fs，空间差分步长为1 nm，即每0.1 fs计算一次，每1 nm分为一层。NiTi合金的相关物理参数见表1。

表1 NiTi合金的参数[15]

3 计算结果与分析

图1a和1b给出了双温方程模拟的电子和晶格的时间-空间温度场。可以看到，在飞秒激光作用下，电子温度在几百飞秒内迅速升高，高温电子通过碰撞进行能量传递，使其系统的峰值温度达到3050 K，再通过电子热扩散将激光的能量传递到靶材内部，而此时由于晶格不能直接吸收激光能量，其温度仍比较低。然后电子通过剧烈的电声耦合作用将能量快速地传递给晶格，使晶格接受能量温度不断升高，电子温度不断下降，最终两者的温度都在1300 K左右，达到热平衡状态，整个能量耦合的非平衡过程在10个皮秒左右完成[16,17]。就传递深度而言，电子在峰值温度时传递深度约为20 nm，晶格在平衡状态时的传递深度也在20 nm左右，可见飞秒单脉冲的作用只发生在材料表面，对材料内部的影响并不明显。由此可见，飞秒激光加工材料时，在超短时间内通过极高的激光功率作用于工件，在飞秒时量级时间内，使材料从固态瞬间变为高温、高压的等离子体状态，以喷射的形式脱离被加工材料，实现了材料的非热熔加工。因为脉冲的持续时间极短，温度来不及向周围扩散就发生了烧蚀，因此热影响区和热扩散的作用也很小，所以利用飞秒激光可以实现血管支架的精细加工。

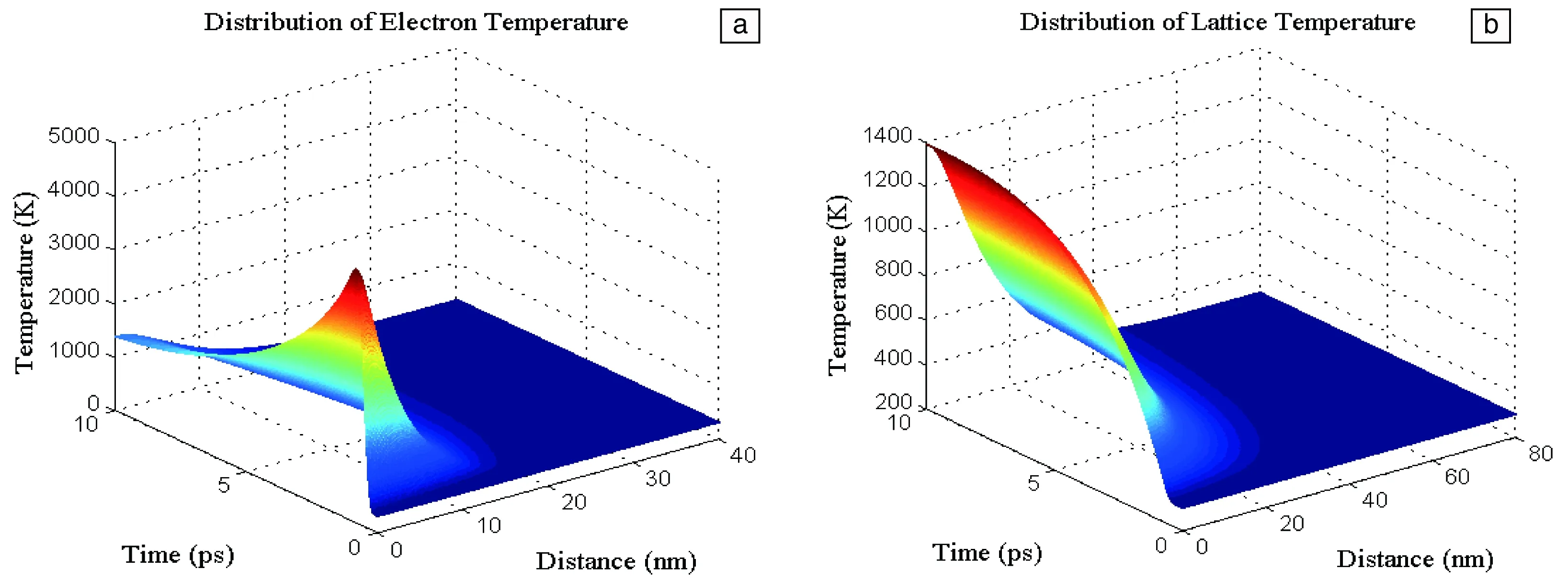
图1 电子温度(a)和晶格温度(b)分布Fig.1 Distribution of electrons temperature (a) and lattices temperature (b)

在其他参数一定的情况下，选择不同的脉冲能量密度进行数值模拟，得到电子与晶格温度场变化规律如图2所示。图中显示随着脉冲能量密度的增大，电子的峰值温度会随之增大，在脉冲过后电子的温度也会增加，最终使得电子和晶格的平衡温度也有所升高。达到耦合状态的标志是晶格和电子的温度达到一致，不随时间的延长而变化，在图上观察到的现象就是曲线开始变得平缓。在图2a和2b中可以看出能量为100 J/m2时，4 ps左右曲线变得平滑，也就是说此时达到了耦合状态。800 J/m2时，直到9 ps左右曲线才开始平缓，标志着此时电子和晶格的温度一致。随着能量密度的增大，耦合时间延长。如果激光的能量密度继续升高，当电子和晶格耦合时间超过晶格和晶格的热平衡时间，热扩散就会对烧蚀周围区域的材料造成影响，烧蚀的过程将会是“热”作用。由此推论对于不同的脉宽应该有一个临界的能量密度值，当激光的能量密度小于此值为相对意义上的“冷”加工，超过这个值将产生一定热作用，将对加工区周围材料和加工后的工件质量产生一定影响。因此为了进一步提高加工质量和加工精度，首先应该找到这个临界的能量密度值。这个结论对实际应用飞秒激光加工血管支架有重要的理论指导。

选取不同的脉冲宽度进行数值模拟，得到电子与晶格温度场变化规律如图3所示。从图中可以看出，能量密度相同的情况下脉冲宽度越小，电子温度上升的速度越快，达到的峰值温度越大，所用时间也越短，而最终的电子温度却变化不大。对于晶格而言，脉宽越小，晶格的温度变化越快，和电子的耦合时间越短，最终的平衡温度基本相同，与文献[18]的结果相近。上述结果与飞秒激光烧蚀的时间有关，激光的脉冲宽度越窄，靶材的电子在极短时间内吸收的激光能量越大，所以电子温度快速升高，达到的峰值温度也越大，电子通过电声耦合作用把能量传递给晶格，因此晶格温度上升的速度也会变快，达到平衡状态时所需要的时间越短。实际的激光器脉宽为300 fs，通过以上分析可知，该参数可以实现血管支架的精密加工。

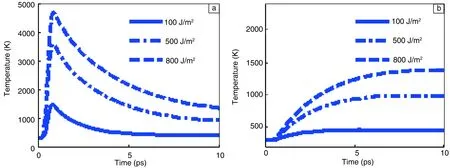
图2 不同激光能量密度下，电子(a)和晶格(b)的温度分布Fig.2 Distribution of electrons temperature (a) and lattices temperature (b) under different laser energy densities

图4分析了延迟时间分别为50 fs，150 fs，l ps和6 ps时，NiTi合金材料不同深度处的电子和晶格的温度变化。

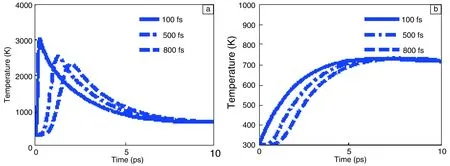
图3 不同激光脉冲宽度下，电子(a)和晶格(b)的温度分布Fig.3 Distribution of electrons temperature (a) and lattices temperature (b) under different laser pulse width

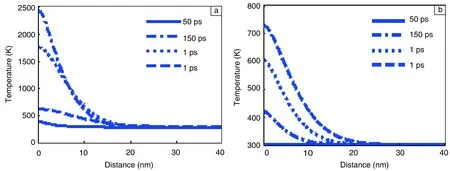
图4 不同延迟时间下，电子(a)和晶格(b)的温度分布Fig.4 Distribution of electrons temperature (a) and lattices temperature (b) with different delay time

从总体来看，随着深度的不断增加，电子和晶格温度均呈指数衰减。延迟时间在150 fs以内时，表层电子温度在不断上升，到150 fs温度达到最大值约为2500 K，此后由于电子和晶格的耦合作用，电子的温度不断下降，6 ps左右达到最小值约为700 K。与此同时，随着电声耦合作用晶格温度不断上升，最终在6 ps左右和电子达到平衡状态，表明此时整个耦合过程已经完毕。距表面20 nm以下温度没有变化，说明整个热传导过程只涉及到材料表面下20 nm处。因此如果合理控制飞秒激光的加工参数，可以实现NiTi合金血管支架的高精度加工。

4 结 论

为了研究飞秒激光烧蚀血管支架材料的温度场分布，以NiTi合金为例，利用双温模型对飞秒激光烧蚀血管支架材料进行了数值模拟。得到了电子和晶格随时间和烧蚀深度的温度变化规律，并讨论了激光能量密度、脉冲宽度、延迟时间对电子和晶格的温度变化影响。计算结果表明：①在飞秒激光作用下，首先是靶材的电子温度急剧升高，然后通过电子和晶格的耦合作用，将能量传递给晶格，最终两者达到热平衡状态；②激光能量密度越大，电子达到的峰值温度越大，最后电子和晶格的热平衡温度也越高；③激光的脉冲宽度越小，电子和晶格的温升越快，达到平衡状态的时间越短；④随着烧蚀深度的增加，电子和晶格的温度都呈指数递减，热传导深度仅为几十纳米。通过以上结论分析，得出了影响飞秒激光烧蚀NiTi合金血管支架材料过程的几个因素，对提高飞秒激光加工NiTi合金血管支架的精度和效率有重要的意义。

References

[1] Dotter C T, Buschmann R W, McKinney M K,etal.Radiology[J], 1983, 147(1): 259-260.

[2] Wu Yuanhao(吴远浩),Zhou Xiaochen(周晓晨),Li Nan(李楠)，etal.MaterialsChina(中国材料进展)[J],2012,31(9):27-34.

[3] Meng Xianglong(孟祥龙),Cai Wei(蔡 伟).MaterialsChina(中国材料进展)[J],2011,30(9):13-20.

[4] Muhammad N, Whitehead D, Boor A,etal.AppliedPhysicsA[J], 2012, 106(3): 607-617.

[5] Huang Weidong(黄卫东),Lv Xiaowei(吕晓卫), Li Xin(林鑫)，etal.MaterialsChina(中国材料进展)[J],2011,30(4):1-10.

[6] Gu Xingzhong(顾兴中), Ni Zhonghua(倪中华).JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition)(华中科技大学学报(自然科学版))[J],2007,35(z1):143-146.

[7] Guo Jingzhe(郭景哲),Jia Baoxian(贾宝贤), Wang Dongsheng(王冬生),etal.MachineryDesign&Manufacture(机械设计与制造)[J], 2009 (10): 257-258.

[8] Zhou Yongheng(周永恒), Liao Jianhong(廖健宏), Meng Hongyun(蒙红云),etal.AppliedLaser(应用激光)[J],2005,25(3):161-164.

[9] Cheng Ping(程 萍), Wei Di(位 迪), Wu Benke(吴本科),etal.OpticsandPrecisionEngineering(光学精密工程) [J],2014,22(1):63-68.

[10]Anisimov S I, Kapeliovich B L, Perelman T L.ZhEkspTeorFiz[J], 1974, 66(2): 375-377.

[11]Kim J, Na S.Optics&LaserTechnology[J], 2007, 39(7):1443-1448.

[12]Chen Anmin(陈安民), Jiang Yuanfei(姜远飞), Liu Hang(刘航),etal.Laser&Infrared(激光与红外)[J],2012,42(8):847-851.

[13]Elsayed-Ali H E, Norris T B, Pessot M A,etal.PhysicalReviewLetters[J], 1987, 58(12): 1212-1215.

[14]Ni Xiaochang(倪晓昌), Wang Qingyue(王清月).ChineseJournalofLasers(中国激光)[J],2004,31(3):277-280.

[15]Zhu Shijia(朱诗佳), Wang Xinlin(王新林), Zhu Weihua(朱卫华),etal.Electro-OpticTechnologyApplication(光电技术应用) [J],2011,26(6):39-44.

[16]Yao Hongbing(姚红兵),Yu Wenlong(于文龙),Yang Zhao(杨 昭),etal.ActaPhotonicaSinica(光子学报) [J], 2015,44(4):35-40.

[17]Wang Wenting(王文亭), Zhang Nan(张 楠), Wang Mingwei(王明伟),etal.ActaPhysicaSinica(物理学报) [J], 2013 (21):87-95.

[18]Lu Lizhong(卢立中), Shi Yunfei(石云飞), Xu Chenguang(徐晨光),etal.JournalofJiangsuUniversity(NaturalScienceEdition)(江苏大学学报(自然科学版))[J], 2011,32(2):199-204.

(编辑 惠 琼)

Numerical Simulation of Femtosecond Laser Ablation of Stent Material

WANG Leilei，ZHENG Yangyang，HUO Yang，LIU Jianying，LI Chunxia， LU Yang

(School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China)

In order to study the characteristics of femtosecond laser ablation of stent material, two-temperature model which considers the thermal conduction between the electronics, and finite difference method were used to simulate temperature field of NiTi alloys during femtosecond laser ablation. According to the results, the influences of laser energy density, pulse width and delay time on the temperature field of electron and lattice were discussed. The results showed that the temperature of electron and lattice finally reached a state of equilibrium. Before that, firstly, the temperature of electron increased rapidly due to energy absorption, then, the absorbed energy was transferred to lattice through electron phonon coupling effect; at last, the equilibrium would be reached. Laser energy density played a major role in the equilibrium temperature, and pulse width determined the peak temperature and the time to reach it. Consequently，the temperature of electrons first increased and then decreased with the increase of the delay time, but lattice temperature only increased with the increase of the delay time. The results may have an important guiding significance to actual processing of femtosecond laser ablation of vascular stent.

femtosecond laser; nickel titanium alloy; vascular stent; two-temperature model; electron temperature; lattice temperature

2015-09-22

国家自然科学基金项目(61303006);山东省优秀中青年科学家科研奖励基金项目(BS2012ZZ009)。

王雷雷，男，1990年生，硕士研究生, E-mail:354019062@qq.com

10.7502/j.issn.1674-3962.2017.03.10

TN249

A

1674-3962(2017)03-0226-05