基于FTA-AHP的铁路安全风险综合评估方法

刘敬辉

(中国铁道科学研究院 铁道科学技术研究发展中心，北京　100081)

铁路运输安全直接关系到人民生命财产安全，并直接与社会的和谐发展密切相关。目前，为保障铁路运输安全，在对铁路进行安全风险评估时大量应用了包括故障树分析法(FTA)[1-4]和层次分析法(AHP)[5-9]在内的安全分析方法。但是上述2种安全分析方法都有其应用的适用范围和局限性，FTA方法通过建立模型可以对目标风险事件的发生原因及其影响程度进行追根溯源，但无法判断目标风险事件的总体安全风险水平；而AHP方法则通过建立层次分析模型评估系统的总体安全水平，但通常情况下采用该方法建立模型时需要的相关数据主要通过观察统计获得，而数据的缺乏则容易造成所建模型存在偏差，从而导致评估结果的偏差。

为解决单独使用上述某一种安全分析方法存在的问题，本文在分析FTA方法和AHP方法各自适用范围和局限性的基础上，结合铁路安全风险评估的特点和要求，提出将FTA方法分析得到的基本原因事件信息作为建立AHP模型的输入数据，将基本原因事件的结构重要度作为构造AHP模型中各层次判断矩阵的依据，设计出FTA方法与AHP方法相结合的铁路安全风险综合评估方法，从而提高了铁路安全风险评估的有效性和准确性，同时可解决只单一应用某种方法进行安全风险评估时评估结果存在的片面性问题。

1　基于FTA-AHP的铁路安全风险综合评估方法

FTA方法的主要思想是以选定的目标风险事件为目标，根据对与目标风险事件有关的原因事件及其相互作用的逻辑关系分析，建立有向的故障树模型(以下简称FTA模型)；再通过该FTA模型分析各原因事件对目标风险事件的影响程度，从而为有针对性地制定最优化的安全控制措施提供科学依据。该方法可以综合考虑零件、部件或子系统故障对系统故障的影响，包括人为因素和环境条件等在内，适用于对影响系统安全因素的综合分析。

AHP方法的主要思想是将复杂的系统分解成若干个层次及其对应的若干个影响因素，然后通过逐层比较各个影响因素对其上层因素的影响大小，得出反映各影响因素重要程度的权重，再结合对影响因素安全状态水平的打分，分析得到系统的总体安全水平分值。该方法具有定性和定量相结合的优点，适用于复杂系统受多个因素影响且各因素之间存在明显类别划分或层次关系情况下的综合安全状态评估。在构建AHP模型的过程中，如何更有效地构建影响因素的层次结构并科学确定各影响因素的权重将直接影响AHP分析结果的合理性。

对于铁路的安全风险评估而言，既要分析目标系统发生故障的原因，从而为有针对性地制定安全控制措施提供依据；又要综合考量其总体安全状态，从而为各系统安全水平的横向对比或系统的发展趋势预测提供依据。因此，本文根据对FTA法和AHP法特点的分析，结合铁路的特点及其安全风险评估的要求，将FTA法和AHP法的优势相互结合，研究并提出基于FTA-AHP的铁路安全风险综合评估方法，其流程如图1所示。

图1基于FTA-AHP的铁路安全风险综合评估方法流程

1.1　建立FTA模型

由图1，首先采用FTA法，确定要分析的目标风险事件，以目标系统结构框图、工作流程图、子系统及部件间的接口关系等信息为基础信息，依次分析导致目标风险事件发生的直接原因事件、中间原因事件，直至基本原因事件。由于铁路系统属于典型的复杂人—机—环系统，任何系统故障的原因不仅与系统自身设备/设施的故障有关，还与管理程序、人员操作及社会和自然等外部环境因素的干扰直接相关，因此在分析目标风险事件原因的过程中，应综合分析上述人—机—环及管理的各个方面，此时，历史事故、故障信息及日常安全检测/监测信息应作为重要参考依据。

此外，不同系统即使出现同一种故障，其发生原因也可能存在较大差异。例如，与普速铁路相比，高速铁路由于运行速度高，任何安全隐患，尤其是一些在普速铁路上不会产生大危害的异物侵限、大风、降雨、降雪等外部环境因素都可能对其运行安全产生巨大影响。因此在FTA建模过程中，应具体结合系统的特点展开。

通过上述方法建立FTA模型后，即可以开展定性或定量分析。基本原因事件的结构重要度通常是最直接反映其对目标风险事件影响程度的指标[10]。

定义故障树的结构函数为

φ(x1,x2,…,xn)=

其中，

i=1,2,…,n

式中：n为由故障树分析所得基本原因事件的数目，x1,x2,…,xn为描述基本原因事件状态的布尔变量。

则第i个基本原因事件的结构重要度为

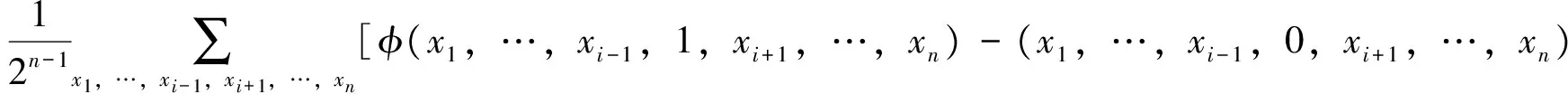
(1)

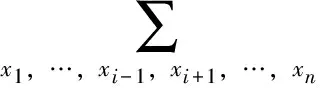
由式(1)可得到定量化的各基本原因事件对目标风险事件的影响程度。

1.2　建立AHP模型及构造判断矩阵

1.2.1建立AHP模型

采用AHP方法，将由FTA方法分析得到的各基本原因事件作为因素，对其按一定逻辑分类并进行归纳，形成有序的准则层和指标层，构建层次结构模型(以下简称AHP模型)。在AHP模型中上层中的因素支配着下一层中的因素，或被下一层中的因素所影响。

1.2.2判断矩阵及其一致性检验

判断矩阵是进行层次分析的基础，可通过对准则层或指标层因素两两比较其对上一层因素影响的重要性得到。

设某准则层或指标层X有n个因素，即X={x1,x2,…,xn},通过比较它们对上一层因素的影响重要性，得到判断矩阵A为

A=(aij)m×n

(2)

式中：aij表示第i个因素相对于第j个因素的比较结果。

在两两因素的重要性比较过程中，由故障树分析获得的基本原因事件结构重要度、各专业领域专家的经验或历史事故或故障的数据可作为决策的基础依据。aij的取值[11-13]见表1。

表1　判断矩阵中比较结果的取值标准及其含义

按照参考文献[14]计算每层判断矩阵的最大特征值及各因素对应的特征向量，并对判断矩阵进行一致性检验。若检验通过，特征向量(归一化后)作为某层各个因素对于上一层各个因素影响的权重向量；若不通过，需要修正判断矩阵。判断矩阵一致性检验的过程如下。

(1)计算一致性指标CI。

(3)

式中：λmax为判断矩阵的最大特征值。

CI越小，说明判断矩阵的一致性越好；否则说明判断矩阵的一致性越差。

(2)计算检验数CR。

(4)

式中：RI为同阶平均随机一致性指标。

如果CR<0.1，则判断矩阵的一致性符合要求；否则判断矩阵的一致性不满足要求，需要对该判断矩阵进行修正。

1.3　安全风险综合评估

首先结合铁路运营事故、故障数据及各专业专家的现场经验，组织专家对指标层各因素的安全状态按预先设定的规则进行打分。在制定打分规则时，对于涉及安全的关键系统，因为要求其运用性能的安全和可靠性较一般系统更高，所以打分愈严苛。例如高速列车的制动系统直接关系着列车运营安全，可采用如表2所示的安全评分标准。

表2　高速列车制动系统的安全状态评分标准

专家对指标层各因素的安全状态按照设定的规则进行打分,然后由下式可得到其所对应(影响)的准则层因素的安全状态的评分y，即

(5)

式中：wi和fi分别为指标层第i个因素的权重向量和安全状态分值。

由所得到的准则层因素的安全状态评分以及权重向量，仍按式(5)计算对应上一准则层因素的安全状态评分，以此类推，直至目标层，则最终可得到目标层因素的安全风险综合评估结果。

2　方法验证

以高速列车制动系统的安全风险评估为例，验证本文方法的可行性和优越性。制动系统是高速列车运行的安全保障，按照功能要求，高速列车制动系统既要能够实现正常运行下列车进出车站时的常用制动功能，又要具备在非常规情况下紧急制动的功能。因此与普速列车相比，高速列车在运行中具有相当大的运动能量，其制动系统任何小的故障或外在影响都可能危及列车运行的安全。

2.1　高速列车制动系统FTA模型的建立及分析

以高速列车制动系统故障为目标风险事件，建立的FTA模型(部分)示例如图2所示。

由图2得到的22个基本事件见表3。

2.2　高速列车制动系统AHP模型的建立及安全状态综合评估

以高速列车制动系统为目标层因素，结合上节对高速列车制动系统FTA模型的分析结果，构建高速列车制动系统的AHP模型。即将FTA模型中的基本原因事件划分为6类，分别对应高速列车制动系统AHP模型准则层中的因素B1—B6。该准则层中各因素及其对应的指标层因素见表4。

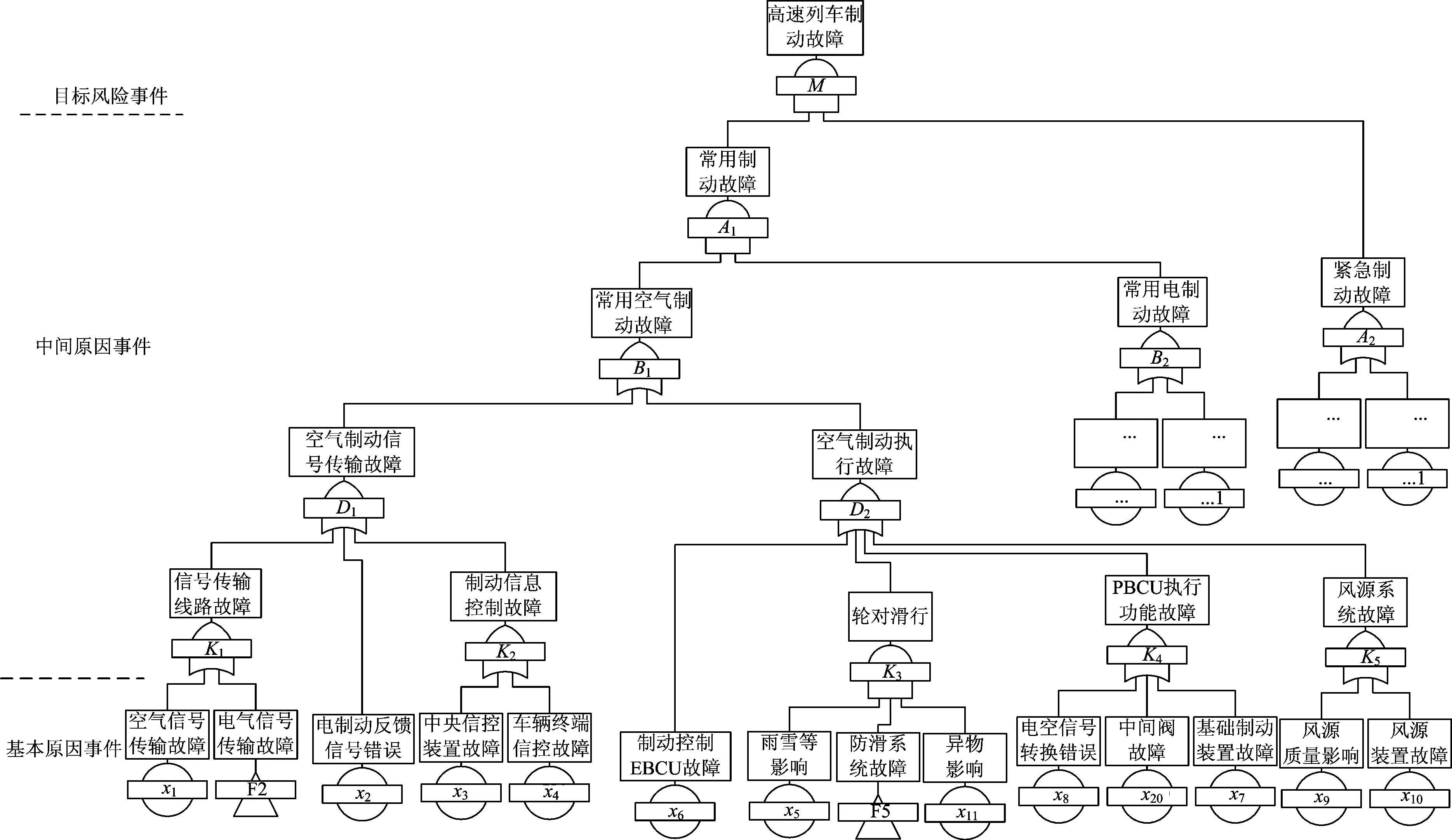
图2　高速列车制动系统的FTA模型(部分)示例

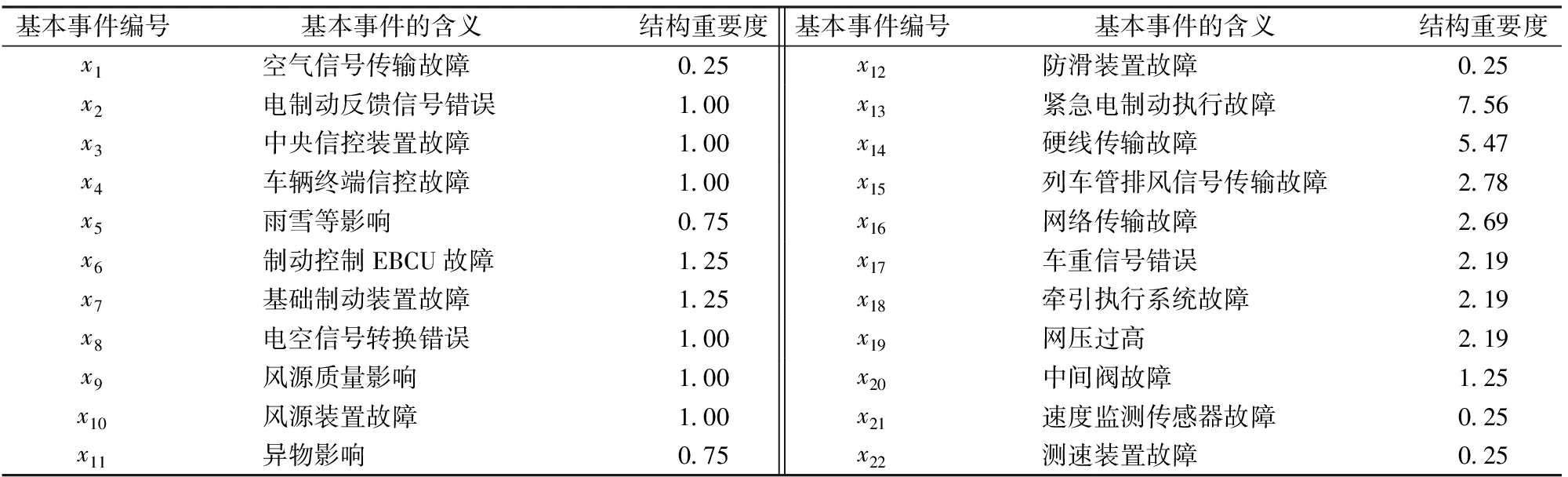
基本事件编号基本事件的含义　结构重要度基本事件编号基本事件的含义结构重要度x1空气信号传输故障025x12防滑装置故障025x2电制动反馈信号错误100x13紧急电制动执行故障756x3中央信控装置故障100x14硬线传输故障547x4车辆终端信控故障100x15列车管排风信号传输故障278x5雨雪等影响075x16网络传输故障269x6制动控制EBCU故障125x17车重信号错误219x7基础制动装置故障125x18牵引执行系统故障219x8电空信号转换错误100x19网压过高219x9风源质量影响100x20中间阀故障125x10风源装置故障100x21速度监测传感器故障025x11异物影响075x22测速装置故障025

表4高速列车制动系统AHP模型准则层因素与指标层因素的对应关系

序号准则层因素指标层因素1牵引侧状态B1x18，x192信号传输通道B2x14，x163机械执行系统B3x12，x7，x1，x15，x21，x22，x8，x204电气执行系统B4x2，x3，x4，x6，x13，x175风源系统B5x9，x106外部环境B6x5，x11

按照表1所示准则分别构建各层的判断矩阵。首先根据指标层各因素所对应基本原因事件的结构重要度，进行因素重要性的两两比较。即当比较i因素和j因素时，如果i因素所对应基本原因事件的结构重要度大于j因素所对应基本原因事件的结构重要度时，则认为其对上面准则层或总目标层的重要性更大；如果两者的结构重要度相同，则进一步依据专家经验或历史事故和故障发生概率等信息进行判断。

依照上述构建判断矩阵的方法建立的高速列车制动系统的总目标层判断矩阵见表5。

由式(3)和式(4)计算目标层判断矩阵的一致性指标CI为0.099 4，CR为0.08<0.1；其他各准则层判断矩阵的一致性指标CI和CR也均达到要求。

按照文献[14]的方法计算指标层各个因素的权重向量，以及组织专家对指标层各因素的安全状态进行评分；然后继续按照文献[14]的方法计算准则层各因素的权重向量，并由式(5)计算其评分。结果见表6。

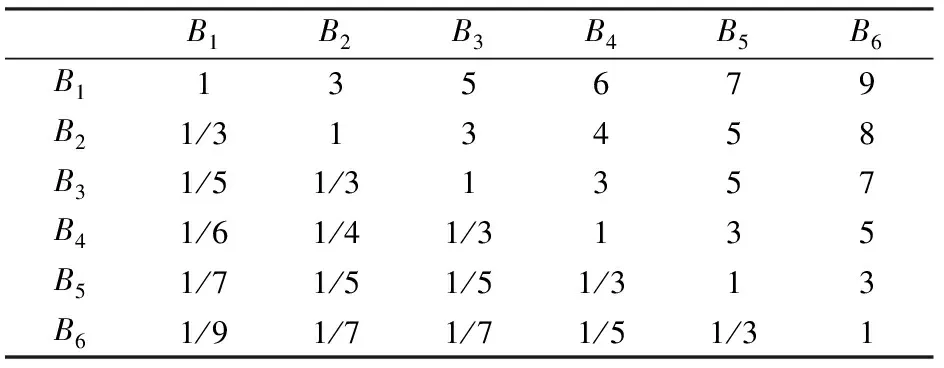
表5　高速列车制动系统AHP模型目标层的判断矩阵

表6高速列车制动系统AHP模型各层因素的权重向量及评分

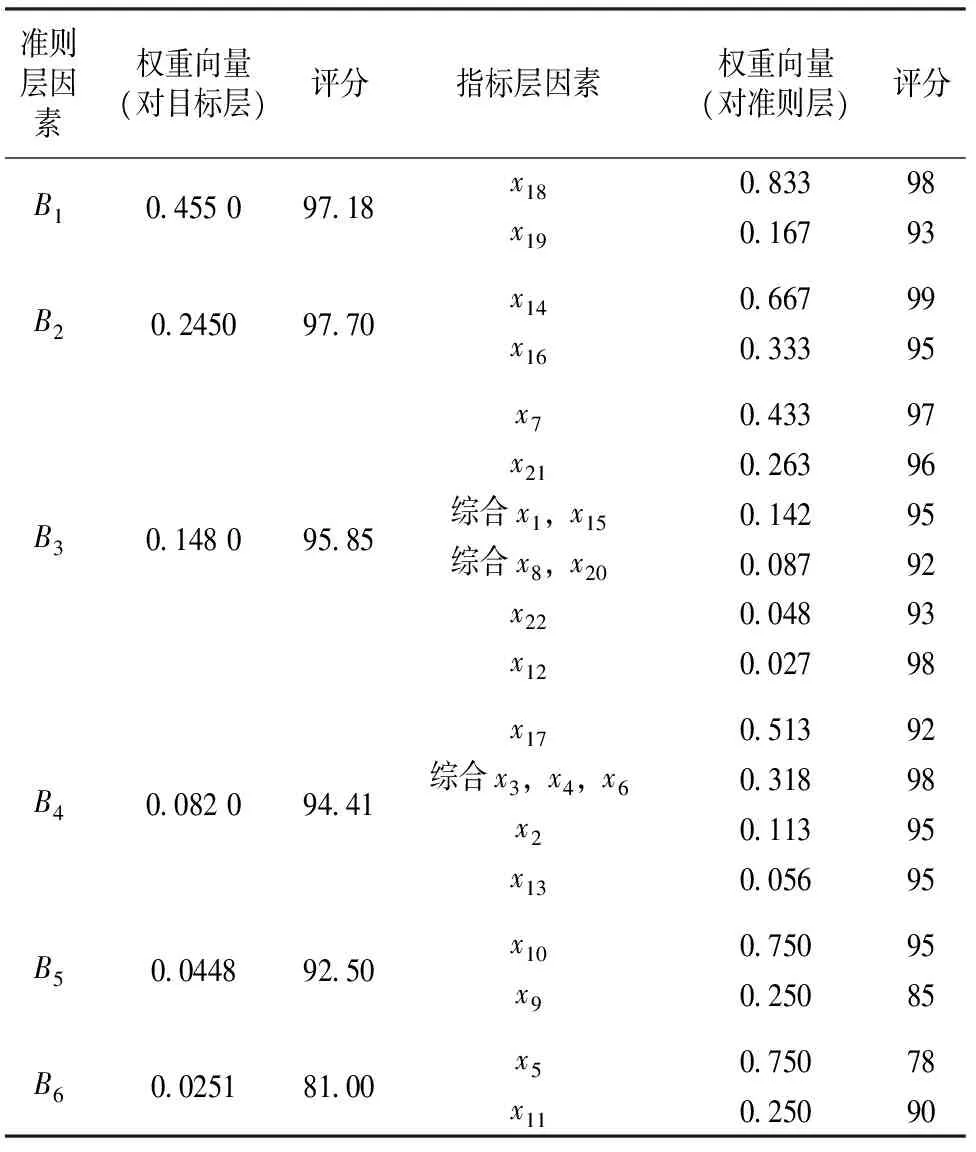
准则层因素权重向量(对目标层)评分指标层因素权重向量(对准则层)评分B1045509718x18083398x19016793B2024509770x14066799x16033395B3014809585x7043397x21026396综合x1，x15014295综合x8，x20008792x22004893x12002798B4008209441x17051392综合x3，x4，x6031898x2011395x13005695B5004489250x10075095x9025085B6002518100x5075078x11025090

由表6和式(5)最后可计算得到整个高速列车制动系统的安全状态综合评估得分为96.28分；按照表2给出的评分标准进行评估，高速列车制动系统的安全性很好，即其发生制动系统故障的风险较低。

由表6还可以看出：高速列车制动系统的牵引侧状态、信号传输通道和机械执行系统的安全状态很好，而电气执行系统和风源系统仍需要改进，改进的主要对象分别是检测监测系统和风源装置的性能；此外，外部环境中影响高速列车制动系统性能正常发挥的主要因素是雨雪，因此需要进一步加强灾害天气的监测和预警。

3　结　语

针对单独使用FTA方法和AHP方法进行铁路安全风险评估时存在评估结果具有片面性的问题，在分析FTA方法和AHP方法的优点和不足的基础上，设计了两者相结合的铁路安全风险综合评估方法。首先建立FTA分析模型，确定目标风险事件的原因事件及结构重要度；然后在此基础上通过分类归纳，建立AHP模型；通过对AHP模型准则层和指标层因素两两比较其对上一层因素影响的重要性，得到各层的判断矩阵；将符合一致性检验条件的各层判断矩阵中的特征向量作为该层对应因素的权重向量，并结合因素的安全状态评分，最终得到目标风险事件的安全风险综合评估结果。

应用所提出的基于FTA-AHP的铁路安全风险综合评估方法对高速列车制动系统进行安全风险的综合评估，结果表明：该方法不仅可以分析系统发生故障的基本原因及其影响大小，还可以对整个系统的安全状态进行综合评估，评估结果能更全面反映系统的安全风险状态，解决了单独应用其中一种方法导致评估结果片面的问题。

[1]张苑，刘朝英，李启翮，等.无线闭塞中心系统安全风险分析及对策[J].中国铁道科学， 2010，31(4)：112-117.

(ZHANG Yuan，LIU Chaoying，LI Qihe，et al. Analysis of the Safety Related Risks of Radio Block Center and Countermeasures[J].China Railway Science，2010，31(4)：112-117.in Chinese)

[2]刘敬辉, 戴贤春, 郭湛，等. 铁路系统基于风险的定量安全评估方法[J].中国铁道科学，2009，30(5):123-128.

(LIU Jinghui，DAI Xianchun，GUO Zhan，et al. Quantitative Safety Assessment Method Based on Risk in Railway System[J].China Railway Science，2009，30(5):123-128. in Chinese)

[3]戚广枫，陈建芳，肖晓晖，等. 高速铁路接触网关键零件的疲劳载荷谱编制[J].铁道学报，2015，37(10)：48-53.

(QI Guangfeng，CHEN Jianfang，XIAO Xiaohui，et al. Fatigue Load Spectrum of Key Parts of High-Speed Railway Catenary[J]. Journal of the China Railway Society，2015，37(10)：48-53. in Chinese)

[4]ANDRIJA Volkanovski, MARKO Cepin, BORUT Mavko. Application of the Fault Tree Analysis for Assessment to Power System Reliability[J]. Reliability Engineering and System Safety, 2009(94):1116-1127.

[5]郭金玉，张忠彬，孙庆云. 层次分析法的研究与应用[J].中国安全科学学报，2008，18(5):148-153.

(GUO Jinyu，ZHANG Zhongbin，SUN Qingyun. Study and Applications of Analytic Hierarchy Process[J]. China Safety Science Journal，2008，18(5):148-153. in Chinese)

[6]陈雷雷，张星臣，王伶俐，等.高速铁路列车服务旅客满意度评价研究[J]. 铁道运输与经济, 2016(6):60-64.

(CHEN Leilei，ZHANG Xingchen，WANG Lingli，et al. Study on Evaluation of Passenger Satisfaction of High-Speed Railway Train Service[J]. Railway Transport and Economy，2016(6):60-64. in Chinese)

[7]李俊芳.层次分析—模糊综合评价法在铁路施工组织方案比选中的应用[J]. 兰州交通大学学报，2013，32(6):82-85.

(LI Junfang. Sound Insulation Analysis of Concrete Wall Based on Finite Element Method[J]. Journal of Lanzhou Jiaotong University，2013，32(6):82-85. in Chinese)

[8]段若晨，王丰华，顾承昱，等. 采用改进层次分析法综合评估 500 kV 输电线路防雷改造效果[J].高电压技术，2014，1(40):131-137.

(DUAN Ruochen，WANG Fenghua，GU Chengyu，et al. Comprehensive Evaluation of 500 kV Transmission Line Lightning Protection Effect Based on Improved Analytic Hierarchy Process[J]. High Voltage Engineering，2014，1(40):131-137. in Chinese)

[9]洪平，刘鹏举. 层次分析法在铁路运营隧道健康状态综合评判中的应用[J]. 现代隧道技术, 2011, 48(1):28-31.

(HONG Ping，LIU Pengju. Application of Analytic Hierarchy Process in Comprehensive Assessment of Health Condition of Railway Tunnels in Operation[J]. Modern Tunneling Technology，2011, 48(1):28-31. in Chinese)

[10]国家标准局. GB7829—87 故障树分析程序[S].北京：中国标准出版社，2004.

[11]储敏. 层次分析法中判断矩阵的构造问题[D].南京：南京理工大学，2005.

(CHU Min. The Construction of Judgement Matrix in Analytic Hierarchy Process[D].Nanjing: Nanjing University of Science and Technology，2005. in Chinese)

[12]JIANG Q M，CHEN C H.A Multi-Dimensional Fuzzy Decision Support Strategy[J].Decision Support Systems，2005，38(1)：91-98.

[13]张炳江.层次分析法及其应用案例[M].北京：电子工业出版社，2014.

(ZHANG Bingjiang. Analytic Hierarchy Process and Its Application[M].Beijing:Publishing House of Electronics Industry， 2014.in Chinese)

[14]喻方元. 线性代数及其应用[M].上海：同济大学出版社，2014.

(YU Fangyuan. Linear Algebra and Its Applications[M]. Shanghai: Tongji University Press,2014.in Chinese)