旋翼柔性梁结构扭转刚度特性分析
张旺亮,石伟兴
(1.中航直升机有限责任公司, 天津 300308;2.中国兵器工业计算机应用技术研究所,北京 100089)
旋翼柔性梁结构扭转刚度特性分析
张旺亮1,石伟兴2
(1.中航直升机有限责任公司, 天津 300308;2.中国兵器工业计算机应用技术研究所,北京 100089)
旋翼柔性梁是整个无轴承旋翼的核心部件,柔性梁在承受巨大的离心力的同时还要满足挥舞、摆振以及变距的刚度要求。由于柔性梁结构不存在实际的变距铰,旋翼的变距操纵要靠柔性梁结构的大变形扭转实现,纤维复合材料可裁剪设计的特性正好满足了这一要求。文章主要针对柔性梁结构的扭转刚度进行了分析计算,分析了八种特殊界面的扭转刚度,比较了复合材料与金属材料的扭转刚度,得出的结论可以为工程上柔性梁的扭转刚度设计提供参考。
柔性梁;扭转刚度;多截面;复合材料桨毂
0 引言
随着先进材料技术的发展,直升机旋翼桨毂越来越多地采用更为简洁的无铰式或无轴承式结构,结构通常采用柔性梁的形式[1]。柔性梁是典型的悬臂梁结构,桨叶的挥舞运动由柔性梁的弯曲变形承担,桨叶的变距运动则由柔性梁的扭转变形承担,变距拉杆将扭矩作用于柔性梁套管,柔性梁套管在柔性梁扭转变形的配合下实现桨叶的变距。西科斯基的RAH-66桨毂以及欧直EC-135旋翼的结构就采用了复合材料柔性梁结构(见图1),其复合材料柔性梁位于中央,负责扭转以及挥舞运动,柔性梁外面有复合材料变距套管,套管同时也具有整流减阻的作用[2]。
柔性梁是无轴承旋翼系统的核心部件,柔性梁结构件的扭转刚度要求尽可能地小,以满足桨叶扭转运动所需的自由度。在具备较低扭转刚度的情况下,还要满足旋转离心力的抗拉刚度与强度要求,适应挥舞、摆振运动的动力学特性要求。与此同时,桨叶的挥舞、变距以及摆振运动的区别不再那么明显,旋翼工作过程中将产生不同于全铰式旋翼的弯-扭气动耦合现象,这对旋翼的气动特性也带来了新的不确定影响。实际工程应用中,多截面结构在节约材料、节约空间等方面也有较多运用,例如MBB公司BO-105验证旋翼的柔性梁采用的就是典型的双截面结构[5]。本文针对几种典型截面柔性悬臂梁结构的扭转刚度进行了分析。
在柔性梁的结构设计过程中,单截面柔性梁的几何选择主要依据铁木辛柯弹性理论。弹性理论主要分析了圆截面等简单截面的扭转刚度。根据弹性理论,简单单连通截面的扭转刚度表达式可以很容易推导出来,这里不再赘述。上述理论的局限性在于,对多连通复杂截面以及更复杂的截面的扭转刚度没有过多涉及,缺乏有效的试验与有限元数据。
因此,对于多截面刚度特性的探究,其方法除了理论与试验以外,有限元方法不失为一种最简便的方法。本文将具体叙述九种不同形状的截面的扭转刚度的有限元分析结果,从而探究最小扭转刚度截面的选择。
1 多截面扭转刚度计算
根据材料力学相关理论,材料的扭转变形主要是材料截面上切应力作用的结果,对于各向同性材料的扭转变形,有以下微分关系:
(1)
即材料的扭转刚度主要受到材料常数G和截面形状IP的影响。对于各向同性材料,当材料的杨氏模量E和泊松比υ确定后,其材料常数G基本确定;而对于纤维复合材料,随着铺层顺序和铺层方向的不同,其宏观材料常数G12是变化的。很显然,G12越小,其宏观材料的扭转刚度也越小。理论和试验表明,单向纤维复合材料的G12最小,在扭转变形过程中,扭转变形产生的切应力仅分布在材料截面上,而纤维方向垂直于材料截面(如图2所示)。
对于截面形状对扭转刚度的影响,铁木辛柯弹性理论主要讨论了圆截面、椭圆截面、三角形截面、工字形等单连通截面的扭转变形[7],对多连通截面的扭转刚度没有涉及。本文采用ANSYS方法计算较复杂截面的扭转刚度大小。扭转刚度试验所选取的不同形状的截面如图3所示。材料选用各向同性材料铝合金,施加扭矩的力臂长度为108mm,施加的力矩分别为2.16、4.05、5.13、6.21、6.804、7.884、9.234N·m共七组。本计算对象截面面积均为100m2,有效扭转长度均为150mm,其截面形状如图3所示,共九种不同形状。
根据控制变量的试验要求,本文计算与试验的对象1-8号截面均保持横截面积不变,并且均以相同面积的圆截面作为比较对象。有限元计算模型与计算结果如图4所示,以8号截面为例。
在此之前我们做了圆截面与矩形截面的有限元计算结果与理论计算结果的对比,计算结果如表1所示。
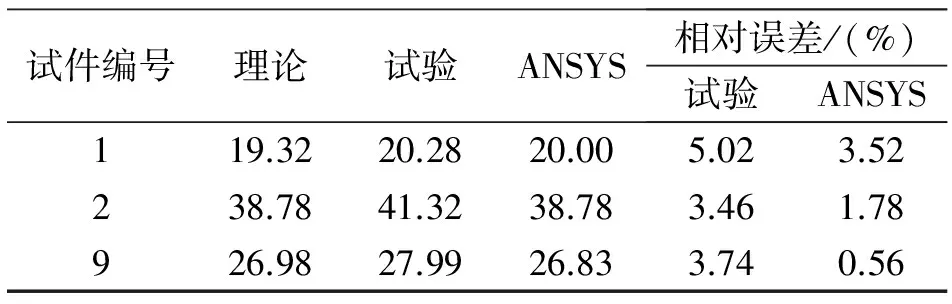
表1 圆截面与矩形截面扭转刚度分析结果(Nm3/rad)
由以上计算与试验结果可以看出,ANSYS计算结果与扭转理论计算结果更为接近,试验结果也佐证了理论分析与有限元结果的可靠性。基于此,下文主要利用有限元手段分析比较了其他复杂界面的扭转刚度大小。根据铁木辛柯扭转刚度理论,施加扭矩大小及梯度保持不变的情况下,本文用Tl/φ的值表示截面扭转刚度的大小。截面扭转刚度ANSYS计算结果对比如图5所示,扭转刚度用角位移表示。
可以看出,不同截面扭转刚度的大小与其截面形状是密切相关的。由以上计算结果我们可以看到,8号截面具有最小的扭转刚度,与同样截面面积的圆截面相比,其扭转刚度减小可达约2.5倍以上。
扭转刚度计算结果表明,与其他截面相比,背对背“双-T”型的截面具有较小的扭转刚度。下节重点分析背对背“双-T”型截面的弯曲、扭转刚度的特性,为柔性梁的截面选择与设计提供帮助。
2 复合材料梁结构扭转刚度分析
上文的分析结果显示“双T”型截面在减小截面扭转刚度方面具有明显优势,下面是针对复合材料剪裁铺层的柔性梁结构进行的扭转刚度有限元分析的结果。材料选用的是T300/5208,探究截面形状对结构扭转刚度的影响,材料参数由表2给出。

表2 T300/5208材料的基本力学性能
柔性梁长L=260mm,单层碳纤布厚度为0.5mm,内部铺层为沿展向0°铺层,共6层,外表面蒙皮铺层为两层±45°铺层。梁截面基本尺寸与基本铺层设计如图6所示。
通过建立有限元模型,并利用前文中同样的分析方法,在梁的端部施加大小为8.5N·m的扭矩,从而计算梁的扭转变形情况。表3列出的是计算结果。图7是有限元模型与等效应力计算结果的云图显示。

表3 ANSYS应力、位移计算结果峰值列表
由以上计算结果可知,复合材料各向异性对降低结构扭转刚度效果明显,结构应力与位移均发生了明显的变化。
1)结构扭转变形时,各单元的拉压应力同时存在,内层的等效应力大于外层,且以压应力为主,当柔性梁承受离心力载荷时,可以部分抵消压应力的存在。
2)τxy、τxz在截面的表面处的值大于截面内部,且上下表面切应力方向正好相反,用±45°的外表面铺层来抵抗剪力作用以保护内部的单向纤维是必要的。
3)图7所示为结构扭转变形的情况,变形主要是端面处Y、Z方向的线位移和绕X轴的角位移。表3所列的最大单元扭转变形为0.544rad,端部截面结构扭转变形大于30°。
3 结论
本文通过有限元分析计算的手段,主要对柔性梁截面扭转刚度特性进行了分析,可以得到以下几点结论:
1)扭转刚度计算结果表明,在所选的九种多截面形式中,背对背“双-T”型截面具有较小的扭转刚度,此结论可为柔性梁的截面选择与设计提供帮助。
2)采用纤维复合材料铺层的柔性梁,由于其刚度可设计性的特点,同等截面情况下,其扭转刚度大大减小。
以上相关结论可帮助我们进行无轴承旋翼柔性梁的结构设计,无轴承桨毂结构中,小的扭转刚度意味着旋翼操纵特性的提高。同时,桨毂扭转刚度的确定也要和截面其他两个方向的弯曲刚度(挥舞、摆振刚度)进行协调。对于具体的柔性梁结构,小的扭转刚度常常伴随着小的挥舞刚度,而此时摆振方向的刚度是比较大的。在工程设计中,可对柔性梁截面形状进行分段刚度设计,如在桨毂根部附近尽量适应扭转刚度和挥舞刚度,而在桨毂端部附近可尽量适应摆振刚度的调整,这样柔性梁段可同时满足三个方向的刚度需求。在柔性梁动力学分析与设计中,改变截面的刚度可很好地调整旋翼系统的挥舞、摆振频率的变化,同时对改变振动过程中弯-扭耦合的影响也有帮助。
[1] 李满福, 陈锦涛, 王清龙. 国外旋翼桨毂构型技术综述[J]. 直升机技术, 2010(4): 64-70
[2] Wang J M. Theoretical and Experiment a1 Research in Aeroelastic Stability of an Advanced Bearingless Rotor for future Helicopters[C]. AIAA 91-0192, 29th Aerospace Sciences Meeting, January 7-10, 1991/Reno, Nevada.
[3] 杨乃宾, 倪先平. 直升机复合材料结构设计[M]. 北京: 国防工业出版社, 2008.
[4] Bernhard A P F, Chopra I. Analysis of a Bending-Torsion Coupled Actuator for a Smart Rotor with Active Blade Tips[J]. Smart Materials and Structures, 2001(10): 35-52.
[5] 沈观林, 胡更开, 刘 彬. 复合材料力学(第2版)[M]. 北京: 清华大学出版社出版社, 2013.
[6] Nakadate M, Tgguchi H, Takaki J.Design and Test Evaluation of FBR Bearingless Main Rotor[J]. Journal of American Helico pter Society, 2001,46( 2):107-116.
[7] 铁木辛柯S P, 古地儿J N, 著,徐芝纶,译. 弹性理论[M]. 北京: 高等教育出版社, 2013.
[8] Gessow A, Myers G C, JR. Aerodynamics of the helicopter[M].New York: Frederick ungar publishing CO. Eighth Printing, 1985.
[9] 马兵林. 星形柔性旋翼桨叶固有振动特性工程计算方法[J]. 直升机技术, 1994(4): 16-20.
[10] 沈亨业, 樊光华. 浅析我国直升机技术发展问题[J]. 直升机技术, 1998(1): 46-51.
[11] 张呈林, 张晓谷, 郭士龙, 等. 直升机部件设计[M]. 南京: 航空专业教材编审组, 1986.
声 明
本刊已加入“中国核心期刊(遴选)数据库收录期刊”、“中国学术期刊(光盘版)收录期刊”、“万方数据—数字化期刊入网期刊”和“超星期刊域出版平台”,本刊已许可上述电子杂志社在其网站及其系列数据库产品中以数字化方式复制、汇编、发行、信息网络传播本刊全文。任何稿件在本刊刊出,即表明该文章所有作者都已认可其版权至本刊编辑部,著作权使用费与本刊稿费一并支付,本刊与国内外文献数据库或检索系统进行合作交流时,不再征询作者意见。作者如有异议,须提前向本刊声明。
《直升机技术》编辑部
Analysis of Torsional Stiffness Properties of Rotor Flexbeam
ZHANG Wangliang1, SHI Weixing2
(1.AVICOPTER CO., LTD,Tianjin 300308, China;2.NORINCO GROUPNorth Information Control Group CO., Ltd. Beijing 100089,China)
A rotor flexbeam is a core component of a bearingless rotor. Different from the conventional cantilever structure, a rotor flexbeam needs bear huge centrifugal force, while meeting the different stiffness, requirements of the flapping, the lagging and the pitching. Because there is no actual variable pitch hinge in the flexbeam structure, the variable pitch control of the rotor depends on the large deflection of the flexbeam structure. The characteristics of the fiber composites that can be tailored just meet the requirements. In this paper, some flexbeam torsion stiffness was analyzed and calculated, eight kinds of special interface torsion stiffness were analyzed. The torsion of composite materials was compared with metal material stiffness. The conclusion could provide reference for engineering design of torsional stiffness of flexbeam.
flexbeam;torsional stiffness;multi section;composite hub
2016-10-24
张旺亮(1983-),男,江西景德镇人,大学,工程师,主要研究方向:项目管理。
1673-1220(2017)01-031-05
V214.1+1
A

