倾转旋翼结构动力学设计技术研究

喻国瑞，贾良现，黄 珺

(中国直升机设计研究所，江西 景德镇 333001)

倾转旋翼结构动力学设计技术研究

喻国瑞，贾良现，黄 珺

(中国直升机设计研究所，江西 景德镇 333001)

通过先进气动外形缩比倾转旋翼的动力学设计，对倾转旋翼结构动力学设计中的特殊问题和重点问题形成了系统的研究，并提出了倾转旋翼结构动力学的工程设计准则和设计方法；基于该准则和方法设计的缩比倾转旋翼已用于风洞试验。

倾转旋翼；旋翼动力学；设计技术

0 引言

倾转旋翼机是一种同时具备直升机、固定翼飞机特点的新型飞行器。当其旋翼处于垂直位置时，倾转旋翼机类似于双旋翼横列式直升机，可悬停、侧飞、后飞、垂直起降，此时它的单位功率起降重量接近典型直升机；当旋翼处于水平位置时，倾转旋翼机就相当于固定翼飞机，能作高速远程飞行。因此，倾转旋翼已成为未来最具发展前景的飞行器之一[1]。

旋翼是倾转旋翼机的主要升力系统(直升机模式)、推进系统(飞机模式)和重要飞行控制执行系统，在工程设计中占有重要地位。在倾转旋翼设计的第一阶段，须非常谨慎地对旋翼动力学部件进行结构动力学特性设计，这项工作与桨叶对于周期谐波载荷的动力学响应密切相关[2]，设计的好坏直接关系到结构的振动和寿命。

倾转旋翼结构动力学设计技术是指运用现代设计理论，结合经验，经过创造性的思维、规划及合理的设计计算，使旋翼结构动力学设计满足倾转旋翼功能和性能要求的技术。本文基于先进气动外形倾转旋翼的设计，研究总结了倾转旋翼结构动力学设计的重要内容和方法，完成的先进气动外形缩比倾转旋翼已成功用于风洞试验。

1 设计技术研究

本文首先研究总结了影响倾转旋翼结构动力学设计的特殊因素和旋翼的构型选择问题，之后研究了桨叶等效边界条件和动力学建模方法，并基于该方法研究了旋翼桨叶的耦合模态，最后总结研究了调频设计准则(图1)。

1.1 影响结构动力学设计的特殊因素

倾转旋翼机特殊的工况及气动外形是造成其结构动力学设计特殊性的来源，贯穿整个旋翼结构动力学设计。

1.1.1 特殊工况

倾转旋翼机具有飞机和直升机两种飞行模式，因此其旋翼具备了多种特殊工况，经过设计梳理，两种模式下对旋翼结构动力学设计有重要影响的工况为：

1) 具有2个工作转速。倾转旋翼机为实现较高前飞推进效率，在飞机模式下旋翼转速会较直升机模式时低。通常，飞机模式旋翼转速比直升机模式降低约25%～40%[3]。

2) 旋翼工作总距范围大。在直升机模式时，一般使用总距不会超过15°，而在飞机模式时，总距能达到35°～ 60°[4]。

3) 气动环境差异性大。在直升机模式时，旋翼的入流不垂直于桨盘平面，存在明显的周期气动激励，旋翼具有周期变距功能，在无穷远处垂直于桨盘的气流速度为0；而对于飞机模式，旋翼入流则垂直于桨盘平面，旋翼无需周期变距，无穷远处垂直于桨盘的气流速度为前飞速度。

1.1.2 特殊气动外形

旋翼气动性能主要取决于旋翼桨叶的气动外形，而倾转旋翼的特殊气动外形对旋翼结构动力学设计有着重要影响。旋翼桨叶气动外形的特殊性如下：

1) 为兼顾悬停和前飞时的旋翼性能，其桨叶结构扭角可达40deg甚至更大；

2) 旋翼实度大于常规直升机，达到0.14甚至更高，这就使得相同旋翼半径下，桨叶的结构绝对厚度更大。

这样的桨叶外形结合特殊的旋翼转速设计能够优化来流攻角，保证直升机模式与飞机模式均具有合理的升力(拉力)、阻力特性，但这正是倾转旋翼结构动力学设计特殊性的重要来源(图2)。

1.2 旋翼构型选择

旋翼构型选择则决定了动力学设计技术研究的方向，是后续研究的基础。不同旋翼构型具有不同的旋翼动力学特性，其设计分析方法也随之不同。倾转旋翼机存在直升机模式、飞机模式以及两种模式切换的过渡飞行状态；在飞机模式下旋翼转速降低25%～40%，旋翼离心力作用明显降低，采用传统铰接式旋翼会形成一个较大的稳态锥度角，降低飞机模式下旋翼的推进效率。此外，倾转旋翼安装在机翼端部，从安全性考虑，须保证在过渡状态和飞机模式下，旋翼受到扰动后桨叶不产生过大挥舞。因此，倾转旋翼须使用一种挥舞较为刚硬的旋翼。另一方面，机翼是典型的柔性支持系统，因此倾转旋翼的构型选择应考虑尽可能降低柔性支持系统带来的耦合影响，如：地面共振、回转颤振等问题。

经过设计梳理，倾转旋翼机旋翼构型选择应主要考虑四个方面：

1) 尽量避免各种飞行姿态下桨叶出现过大挥舞；

2) 尽量提高飞机模式下旋翼的推进效率(此时旋翼作为推进系统)；

3) 从构型上尽可能多地消除不稳定可能性，降低设计复杂度和风险；

4) 尽量降低桨叶根部结构载荷以提高结构寿命。

当前我国的倾转旋翼在构型上宜采用万向铰式旋翼。从结构设计、新材料、主动控制技术的发展来看，若未来能在技术上解决上述需求，则旋翼构型选择将更加灵活。本文中的倾转旋翼设计就使用了三片桨叶万向铰旋翼(图3)。

万向铰构型的旋翼没有独立的水平铰，无摆振铰，容易设计成摆振刚硬旋翼，避免了倾转旋翼复杂的地面共振问题，弱化了旋翼旋转面内模态与支持系统的耦合；另一方面，万向铰旋翼能保证飞机模式时旋翼具有较小的稳态锥度角。此外，万向铰旋翼的动载荷相对无铰旋翼更小，对桨叶根部的受载有利；其桨盘倾斜直接由旋转平面倾斜完成，不会造成摆振面内的科氏力，这对于前飞状态非常有利[5]。

1.3 动力学建模

为计算分析旋翼动力学特性，需对倾转旋翼进

行动力学建模。倾转旋翼桨叶通常具有40°以上的结构负扭转，桨毂还可能有一定的预锥角，桨叶通常还具有一定的上反角、下反角及比较大的后掠角，桨叶结构复杂。本文对倾转旋翼动力学建模如下：

1)将桨叶离散为一系列的具有不同上反下反角及前略后掠角的Eurler-Bernoulli直梁单元，各梁单元的弹性轴为直线，相邻单元的弹性轴首尾相接。

2)为了方便描述旋转桨叶的空间位置及运动变形，建立一系列的参考坐标系，便于使用哈密顿原理导出动力学方程[6-7]。桨毂坐标系以下标h标识，旋转坐标系以下标r标识，相对桨毂坐标系轴旋转ψ方位角。未变形桨叶坐标系以下标u标识，相对旋转坐标系Jr轴有βG+βP的仰角，βG为万向铰挥舞角,βP为预锥角。桨叶变距轴线坐标系下标p，未变形桨叶坐标系下标c，桨叶单元坐标系下标k，变形剖面坐标系下标d。

各坐标系间的转换关系矩阵为：

(1)

(2)

(3)

其中，θcon为控制桨距输入，Kβ为挥舞变矩调节系数，θs为变矩铰弹性变形。

(4)

其中，Λ1k是后掠角，Λ2k是上反角，Λ3k是结构扭转角。

其中，θt是结构扭转角，φ是弹性扭转角。

3)由哈密顿原理导出倾转旋翼气弹动力学方程：

(6)

其中：

(7)

(8)

(9)

(10)

(11)

mb为桨叶线密度

(12)

(13)

(14)

(15)

(16)

(17)

(18)

{Xkio,Ykio,Zkio}T分别为第i片桨叶的第k个单元弹性轴的首节点在未变形桨叶坐标系内的位置坐标；s为单元坐标系内的局部坐标；{u,v,w}T为第i片桨叶的第k个单元(s,0,0)处弹性轴的弹性位移；ue为弹性伸长。

4)通过求解该非线性动力学方程，即可得到倾转旋翼的结构动力学特性。

1.4 桨叶等效边界条件

全耦合的3叶万向铰旋翼除考虑桨叶自身动力学问题外，还须考虑桨叶之间的刚柔耦合动力学问题，使得设计复杂化。为简化模型以适应工程设计，本文将桨叶根部约束边界条件等效为固支边界和铰支边界来构造“周期型”和“集合型”模态，并得到如下结论：三叶万向铰的挥舞不存在绝对的铰支边界条件，但存在弱固支约束边界，一定程度上可近似看成铰支边界；其完全的固支边界条件是存在的。

在旋转坐标系中，设第m片桨叶根部挥舞力矩按级数展开为：

(19)

设每片桨叶处在等同的周期气动环境中：

(20)

以其中一片桨叶挥舞为基准，在桨毂中心处力矩合成即为该片桨叶总的力矩(挥舞、摆振、扭转)。

则挥舞力矩为：

即：

(21)

摆振力矩为：

(22)

操纵载荷为：

(23)

当系数为2时为集合型运动：其摆振运动表现为扭振系统整体频率，其扭转运动表现为总距操纵刚度下的频率。

当系数为0时摆振表现为完全固支边界条件下的频率，摆振运动支持结构不发生耦合；扭转表现为与横/纵向周期操纵刚度匹配的频率。边界条件系数表如表1。

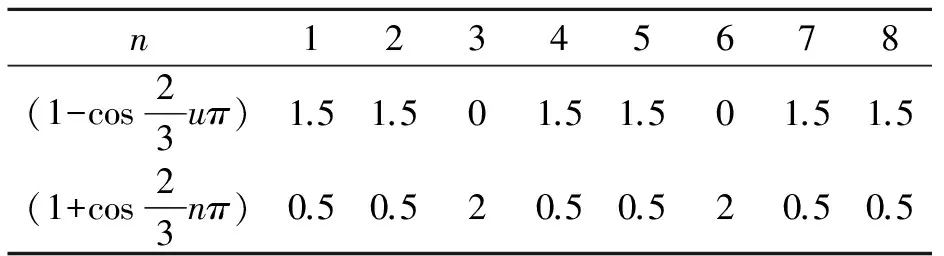
表1 边界条件系数表

故当n为3的倍数时，为挥舞为固支边界条件，当n=1、2、4、5、7……时不存在完全铰接边界条件，此时系数为1.5，为近似铰接的支持条件。因此，三桨叶万向铰式倾转旋翼设计可使用特殊的共振图(图4)。

1.5 旋翼桨叶的耦合模态

桨叶的模态识别是旋翼结构动力学分析的重要内容，桨叶模态特性的不同决定了系统的响应特性。

研究发现，倾转旋翼大范围的总距和转速变化，加之桨叶的大结构扭角造成了挥舞模态、摆振模态和扭转模态之间强烈的耦合，这种耦合还伴随着总距而变化，使得桨叶模态呈现出特殊性质。

图5和图7分别为倾转旋翼周期型和集合型模态中的模态振型包络线，其中第一个case表示-4°总距，最后一个case为52°总距；图6和图8分别对应了-4°～52°总距范围内周期型和集合型各阶模态频率变化。可以得到如下规律：

1) 频率8Ω以下的周期型第2阶、第3阶模态，集合型第1阶、第2阶模态的挥舞和摆振具有强烈的耦合，不能直接判定其为挥舞模态或摆振模态，建议称其耦合模态。

2) 周期型第2阶、第3阶模态均同时表现出挥舞2阶和摆振1阶模态的特性。第2阶在小总距时以挥舞特性为主，在大总距时以摆振特性为主，第3阶在各个总距下挥舞和摆振相当。

3) 周期型第2阶模态频率随总距升高迅速降低；周期型第3阶模态频率随总距升高呈现先迅速提高后迅速降低的规律；扭转一阶频率在10°以下趋于平稳，之后随总距的升高呈现先降低后增高的规律。周期型第3阶和扭转1阶频率变化的拐点十分接近。

4) 集合型则是第1阶、第2阶模态同时表现出挥舞和摆振的耦合特征，不同之处在于集合型第1阶表现的是挥舞1阶和摆振1阶的特性，集合型第2阶与周期型第3阶类似，表现出挥舞2阶与摆振1阶模态的特性。第1阶在小总距时以挥舞特性为主，在大总距时以摆振特性为主，第2阶在各个总距下挥舞和摆振相当。

5) 集合型第1阶模态频率随总距升高缓慢降低；集合型第2阶模态频率随总距的升高呈现先缓慢降低，在大总距时迅速降低后又升高的趋势；扭转1阶与耦合2阶的特性类似，频率随总距的升高呈现先缓慢降低，在大总距时迅速降低后又升高的趋势。

1.6 旋翼频率设计准则

调频设计是旋翼结构动力学设计的主要目标之一。倾转旋翼结构动力学特性与强结构耦合(桨叶大结构扭角、大变距范围引起)和大范围的旋翼转速变化紧密联系，这种强烈的耦合使得常规直升机旋翼的按照挥舞和摆振分开调频的办法不再适用，同时，这使得按照传统设计要求的避开nΩ进行调频设计将使得设计无法开展[8，9]。根据上述研究，提出了三桨叶万向铰旋翼初步设计时的结构动力学设计准则如下：

1) 根据桨叶边界条件将旋翼模态分为周期型和集合型进行计算。铰支边界为周期型模态，固支边界为集合型模态。

2) 在直升机模式额定转速、飞机模式额定转速等工作停留转速下，集合型模态固有频率仅须避开1Ω、3Ω、6Ω；周期型模态除挥舞1阶外，其它固有频率仅须避开1Ω、2Ω、4Ω、5Ω。

3) 当某个使用状态中周期型1阶模态以摆振特征为主时，模态频率须大于1.25Ω。

4) 任何周期型模态频率配置距2Ω和4Ω的气动载荷激励0.25Ω以上。

5) 任何集合型模态频率配置距3Ω和6Ω气动载荷激励0.15Ω以上。

6) 对于6/rev及以上的高频模态的频率配置，要求较为放松，初步设计时不作特殊要求。

7) 在设计之初必须首先明确直升机模式和飞机模式的旋翼额定转速和其它停留转速；

8) 由于变距对动力学特性的影响十分突出，故在设计之初就要明确对应转速下需要稳定使用的总距边界。需要注意的是与直升机旋翼设计不同，保守过大的总距使用范围是不可取的。

上述第3-6条所确定的设计边界是工程设计初期的重要参考，但随着设计工作的详细深入，可通过载荷分析等手段逐步放宽要求。

此设计准则最大的意义是扩展了倾转旋翼的频率配置可行区间，使得对总距十分敏感的倾转旋翼固有频率的调频设计成为了可能，解决了由于传统旋翼动力学设计准则导致的使用限制。

2 工程设计案例

旋翼型式：万向铰

桨叶片数：3

旋翼实度：0.144

桨叶结构扭角：35°(非线性扭转)

变距活动范围：0°～50°

飞机模式：35°～50°

直升机模式：0°～15°

万向铰挥舞活动范围：-10°～ +10°

工况：各个设计总距下进行风洞试验

使用本文方法，结构动力学设计结果见表2和表3。图9为该缩比旋翼进行风洞测试。

表2 周期型频率比计算结果

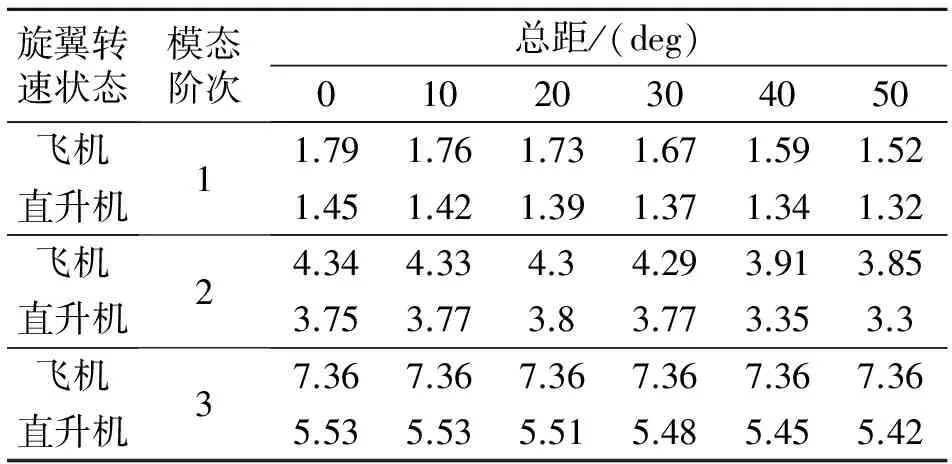
表3 集合型频率比计算结果

3 总结

本文紧密结合实际工程设计，研究总结了倾转旋翼结构动力学设计中所需考虑的重要问题，建立了倾转旋翼动力学模型，研究总结了适用于工程实际的设计思路和设计准则，这些研究揭示了倾转旋翼的结构动力学特点，涵盖了倾转旋翼结构动力学工程设计的重要内容和方法，基于此设计的缩比模型旋翼成功用于风洞试验，有力地支持了本文的研究结果。得出结论如下：

1) 本文建立的动力学模型适用于万向铰式倾转旋翼结构动力学计算分析；

2) 本文提出的边界条件处理方法和模态特性研究对深入认识万向铰式倾转旋翼动力学特性有重要意义；

3) 本文提出的设计准则可用于指导三叶万向铰式倾转旋翼结构动力学工程设计。

[1] 徐 敏. 倾转旋翼机的发展与关键技术综述[J]. 直升机技术, 2003(2):40-44.

[2] 张晓谷. 直升机动力学设计[M]. 北京: 航空工业出版社, 1995: 4-45.

[3] Warwick G. Opposing Tilt [J]. Aviation Week & Space Technology, October 14/21, 2013:1-2.

[4] 王 伟, 段卓毅, 周 林. 倾转旋翼机设计特点及难点浅析[J]. 航空科学与技术, 2015(3):1-4.

[5] 张呈林, 张晓谷, 郭士龙, 等. 直升机部件设计[M]. 南京：南京航空学院, 2008.

[6] Srinivas V, Chopra I, Nixon W. Aeroelastic Analysis of advanced Geometry Tiltrotor Aircraft [J]. Journal of the American Helicopter Society, 2013,43(3):212-221.

[7] Srinivas V, Chopra I. Formulation of a Comprehensive Aeroelastic Analysis for Tiltrotor Aircraft [R]. AIAA-96-1546-CP.

[8] Popelka D A, Agnihotri A. Bell Helicopter Textron Inc. Prediction and Alleviation of V-22 Rotor Dynamic Loads [C]. American Helicopter Society, November 1989:55-79.

[9] Agnihotri A, Schuessler W, Marr R. V-22 Aerodynamic Loads Analysis and Dvelopment of Loads Alleviation Flight control System [C]. American Helicopter Society 4lth Annual Forum, Boston, Massachusetts, May 1989:32-53.

Research and Development of Tilt-rotor Structure Dynamic Design

YU Guorui, JIA Liangxian, HUANG Jun

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

Important and special structure dynamic problem had systemic researched in a project which used 3 advanced geometry blades on a scaled tilt-rotor design. The design criteria of tilt-rotor structure dynamic had been presented. The scale rotor which followed the criteria had work in wind tunnel test.

tilt-rotor； rotor dynamic；design.

2016-11-10

863计划“先进直升机技术”(2012AA112201)。

喻国瑞(1989-)，男，贵州贵阳人，本科，助理工程师，研究方向为旋翼系统动力学设计、复合材料旋翼桨叶结构设计。

1673-1220(2017)01-001-07

V224；V214

A