旋翼桨叶载荷与桨叶结构参数相关性研究
胡 偶,陈平剑
(中国直升机设计研究所,江西 景德镇 333001)
旋翼桨叶载荷与桨叶结构参数相关性研究
胡 偶,陈平剑
(中国直升机设计研究所,江西 景德镇 333001)
基于CAMRAD II软件,建立自由尾迹耦合柔性多体动力学的弹性桨叶结构载荷分析模型,针对某直升机旋翼桨叶结构设计与载荷分析问题,开展桨叶结构参数与桨叶载荷水平的相关性研究。通过典型飞行状态,包括超扭状态和大前进比前飞状态,研究桨叶剖面挥舞刚度、摆振刚度、扭转刚度等参数的变化对桨叶挥舞与摆振方向载荷水平的影响,并分析由结构共振引起的桨叶载荷突增现象。
载荷;结构参数;共振;旋翼桨叶
0 引言
直升机旋翼桨叶载荷分析是旋翼气动设计与结构设计的重要支撑,是旋翼系统方案设计与工程详细设计阶段旋翼桨叶强度与寿命评估的重要依据。旋翼桨叶载荷分析是典型的气动/结构耦合问题,且是一种综合性的系统工作:首先需建立直升机模型、旋翼和尾桨模型以及桨毂-操纵系统模型(包括各种铰结构、变距拉杆等),再将模型通过各种连接形式连接,然后基于气动模型(如升力线方法)和多体动力学模型,开展旋翼桨叶载荷分析。载荷分析工作在旋翼系统设计过程中起着承上启下的重要作用,是结构设计、载荷分析、寿命评估这一设计流程必不可少的关键环节。
旋翼桨叶振动载荷评估是直升机空气动力学与动力学领域面临的难点。受限于复杂的气流环境、非线性结构弹性变形等耦合因素,采用数值分析方法很难获得精确的振动载荷值。但从工程设计的角度来看,通过数值分析与解析分析方法,构建高效、准确的载荷工程计算方法,能够满足不同飞行状态的载荷计算分析工作要求,形成可用于旋翼系统寿命与强度评估的载荷谱,从而有效缩短直升机旋翼系统研制周期,提高研制效率。
在国外,随着计算技术的高速发展,形成了以CAMRAD II[1]为代表的直升机综合气弹分析软件,在直升机工程设计领域得到了广泛的应用。该软件是由Wayne Johnson[1-2]开发的一款直升机气动与动力学综合分析软件,具备多体动力学、非线性有限元以及直升机空气动力学耦合分析能力,可用于预先研究、方案设计、详细设计等阶段直升机的性能、载荷、振动、响应及稳定性分析。CAMRAD II软件在旋翼桨叶载荷计算方面得到了广泛的应用验证[3-7],其精度能够满足工程设计的要求。
在国内,习娟等人[8]针对某无人直升机开展了直升机旋翼系统载荷分析技术研究,王浩文等[9]建立了旋翼系统综合气弹分析方法,孙韬等[10]针对典型前飞状态开展旋翼振动载荷分析研究,吴杰等[11]比较了力积分法、反力法和曲率法三类旋翼桨叶结构载荷计算方法的预测精度和适用范围。
本文基于CAMRAD II软件,建立耦合自由尾迹模型和柔性多体力学思想的弹性桨叶结构载荷分析模型。选取典型飞行状态,开展旋翼桨叶结构参数与桨叶载荷水平相关性分析,通过桨叶剖面挥舞刚度、摆振刚度、扭转刚度等参数的变化,研究桨叶挥舞与摆振方向载荷随桨叶结构参数的变化关系。最后,从桨叶模态分析和载荷谐波分析的角度,揭示了结构共振引起的桨叶载荷突增现象。
1 旋翼桨叶载荷计算模型
直升机旋翼桨叶载荷包括静载和动载,计算状态包括超转、超扭、水平飞行、水平转弯、螺旋转弯、自转下滑等状态[8]。本文分别选取具有代表性的超扭状态和最大速度平飞状态开展桨叶静载荷与动载荷分析。超扭状态模拟的是一种极限悬停状态,旋翼总距设为旋翼失速前的最大允许值,周期变距为零,旋翼转速为正常转速,该状态考核桨叶的静载荷的极限值。
采用CAMRAD II软件,建立弹性桨叶载荷分析模型,主要计算流程如图1所示。
动载荷计算过程中采用的是全机配平模型,桨叶为弹性桨叶模型,取6阶模态和6阶谐波,自由尾迹选取Johnson模型[4];静载荷采用孤立旋翼模型计算,取6阶模态和0阶谐波,自由尾迹选取Johnson模型[4]。
2 旋翼桨叶载荷计算结果及分析
2.1 旋翼桨叶结构参数
以某样例直升机作为分析对象,其旋翼桨叶片数为5片,基准转速(Ω)为258 RPM,最大平飞速度(VMAX)为260km/h。为研究桨叶结构参数对桨叶载荷的影响,首先,设计了一副基础模型桨叶(方案 A),图2给出了计算得到的基础桨叶(方案A)的固有特性。然后,在方案A桨叶的基础上,通过调整桨叶翼型起始段之后剖面的挥舞刚度(EIFALP)、摆振刚度(EILAG)和扭转刚度(GJ)等结构参数分布,形成如表1所示的5个备选桨叶结构方案,其中:在方案A结构参数的基础上,(-)表示结构参数未发生明显变化,+表示参数值提高,-表示参数值降低。
图3展示了各方案桨叶段剖面特性参数的变化,包括桨叶剖面挥舞刚度分布与摆振刚度分布。
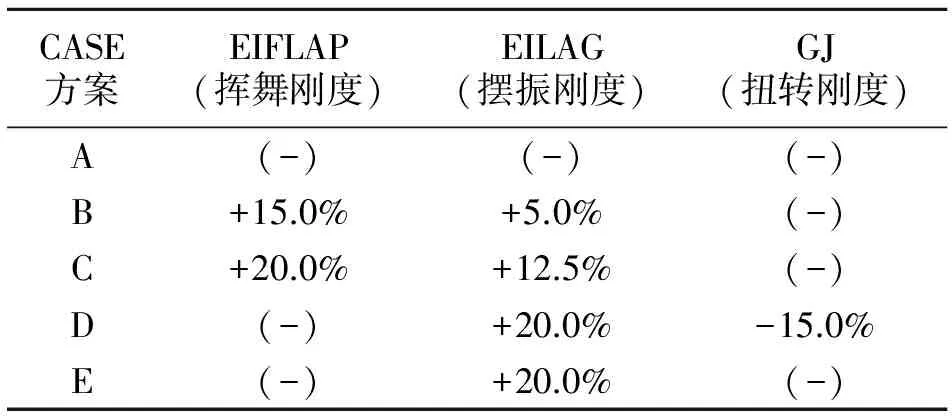
表1 桨叶剖面结构参数的变化
2.2 桨叶载荷与桨叶结构相关性分析
图4展示了超扭状态桨叶静载荷与桨叶结构参数之间的关系,表2给出了桨叶0.5R剖面处的静载荷对比。数值模拟结果表明,桨叶段的剖面挥舞弯矩主要受桨叶剖面挥舞刚度的影响,随着挥舞刚度的增加,桨叶载荷呈线性增加趋势,且剖面摆振刚度变化对挥舞弯矩没有影响;在摆振方向上,桨叶剖面摆振弯矩受摆振刚度和挥舞刚度耦合影响,比较方案C与方案D可以发现,虽然方案D剖面摆振刚度比方案C高7.5%,但由于其挥舞刚度低20%,反而导致方案D的0.5R剖面摆振要小于方案C桨叶。综上,在将叶结构设计时,必须重点考虑桨叶挥舞方向刚度的设计,因为挥舞刚度的变化能够同时引起挥舞与摆振方向载荷的变化。
图5展示了最大速度平飞状态桨叶动载荷与桨叶结构参数之间的关系,表2给出了桨叶0.5R剖面处动载荷对比。数值模拟结果表明,桨叶段动载荷受结构刚度的影响较为复杂,排除方案D桨叶结构,可以发现随着剖面挥舞刚度的增加,剖面挥舞弯矩增大;随着剖面摆振刚度增加,摆振弯矩增大。但是方案D桨叶结构,其载荷变化不满足这一规律,主要表现为摆振弯矩增加显著。
2.3 结构共振引起的载荷突增现象分析
为分析方案D桨叶摆振弯矩突增的原因,对比方案D与方案E桨叶结构,两者的差别在于扭转刚度不一样,方案D的扭转刚度相比于方案E有15%的降低,因此初步确认是由于扭转刚度变化导致载荷发生变化的。
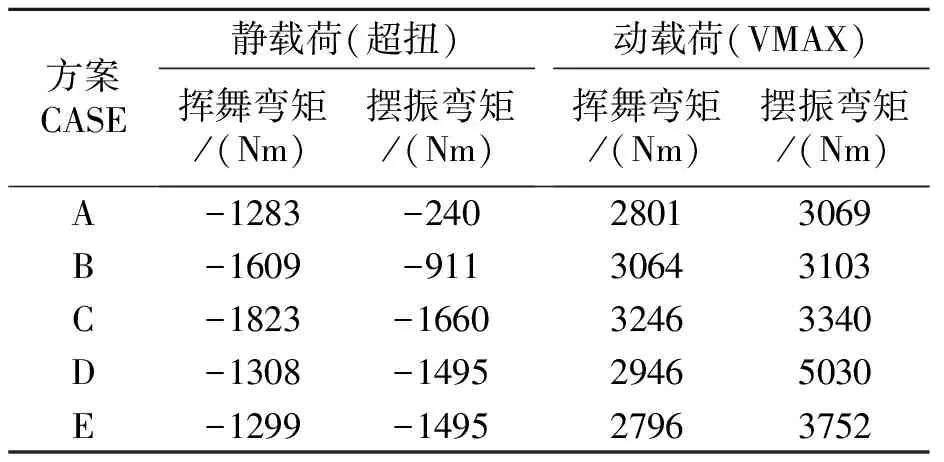
表2 不同桨叶0.5R剖面处桨叶载荷比较
首先,通过模态分析法,取最大速度平飞状态对应的总距值,进行方案D与方案E桨叶结构的固有特性分析,得到如表3所示桨叶固有频率特性。计算结果表明,方案D与方案E桨叶结构前3阶固有频率值一致,但该总距条件下,方案D桨叶结构的扭转1阶频率相比于方案E桨叶更靠近6Ω。因此,从桨叶固有特性分析,导致载荷突增的原因可能是方案D桨叶6阶模态与6Ω靠得近。

表3 方案D与方案E桨叶固有频率比较
取桨叶0.5R处剖面动载荷随方位角变化的关系,如图6所示。挥舞弯矩方案D与方案E的载荷变化趋势一致,而摆振弯矩则两者有显著的差别,方案D桨叶摆振方向载荷在周期内幅值变化剧烈。
为此,对图6中方案D和方案E桨叶的摆振弯矩进行谐波分析[12],获得不同阶次(Ω)下的摆振载荷幅值,如图7所示。通过谐波分析可以看出,对于方案E桨叶结构,随着阶次的增加,摆振弯矩呈减小的趋势,6阶项稍有增大;而方案D桨叶,其摆振6阶项载荷突然增加,载荷呈发散趋势。
因而从桨叶固有频率和载荷谐波分析两个方面可以得出,由于存在摆振-扭转的耦合作用,方案D桨叶结构由于扭转刚度配置不合理,导致直升机以最大速度平飞时,出现结构共振响应,从而引起桨叶载荷高阶项增加,增大了振动载荷水平。
3 结论
以某直升机旋翼为研究对象,开展了桨叶结构设计参数与载荷的相关性分析研究。基于CAMRAD II分析软件,建立了弹性桨叶结构载荷计算方法,并针对桨叶结构设计中的关键参数:剖面挥舞刚度、摆振刚度和扭转刚度的分布等,研究结构参数对桨叶挥舞弯矩与摆振弯矩的影响。研究结果表明,桨叶挥舞与摆振方向载荷主要受挥舞刚度与摆振刚度影响;由于摆振-扭转耦合作用,当扭转刚度布置不合理时,可能引起载荷共振响应现象的产生。通过直升机旋翼桨叶结构与桨叶载荷的相关性分析,摸清桨叶结构参数对桨叶载荷水平的影响,可为桨叶结构设计提供技术支撑,并避免可能产生的结构共振响应现象。
[1] Johnson W. CAMRAD II, Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics[J]. Johnson Aeronautics, 1992.
[2] Johnson W. CAMRAD II, Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics, Rotorcraft Applications[J]. Johnson Aeronautics, 1993.
[3] Johnson, W. Rotorcraft aerodynamics models for a comprehensive analysis[C].Presented at the 54th Annual Forum of the AHS, Washington, DC, May 20-22, 1998.
[4] Johnson, W. A General Free Wake Geometry Calculation for Wings and Rotors[C]. American Helicopter Society 51st Annual Forum, Ft. Worth, TX, May 1995.
[5] Nguyen K, Johnson W. Evaluation of Dynamic Stall Models with UH-60A Airloads Flight Test Data[C]. American Helicopter Society 54th Annual Forum, Washington, D.C., May 1998.
[6] Jones H E, Kunz D L. Comprehensive Modeling of the Apache in CAMRAD II[C]. American Helicopter Society Structure Specialists' Meeting, Williamsburg, VA,October 2001.
[7] Acree C W , Jr. A CAMRAD II Model of the V-22 for Whirl-Flutter Analysis[R]. NASA TM 2004-212801, July 2004.
[8] 习 娟,吴裕平,陈平剑. 直升机旋翼系统载荷分析技术[J].直升机技术,2007, 3: 52-54.
[9] 王浩文,高 正.采用综合气弹分析方法的旋翼非定常气动载荷计算[J].南京航空航天大学学报,2003,35(3): 268-272.
[10] 孙 韬,谭剑锋,王浩文. 典型飞行状态下的旋翼振动载荷计算与分析[J].南京航空航天大学学报,2011,43(3): 302-307.
[11] 吴 杰,杨卫东,虞志浩. 旋翼桨叶结构载荷计算方法比较研究[J].振动与冲击,2014, 33(7): 210-214.
[12] Johnson W. Helicopter Theory[M]. Princeton: Princeton University Press, 1980.
Correlation Study for Blade Loads and Blade Structure Properties of Rotor
HU Ou, CHEN Pingjian
(China Helicopter Research and Development Institute, Jingdezhen 333001, China)
This paper presented predictions of blade structure loads using free wake model and flexible multibody dynamics method based on the CAMRAD II software. The research was focused on the problem of structure design and predictions of blade structure loads, and the relationship of blade structure properties and structure loads was studied. Two typical flight conditions were investigated including over-torque case and high speed case. The blade section properties, such as flap bending stiffness, lag bending stiffness and torsion stiffness were changed to observe how the loads changed. Meanwhile, the resonance phenomenon of blade loads was revealed.
loads; structure properties;resonance;blade
2016-09-23
胡 偶(1984-),男,安徽池州人,博士,工程师,主要从事旋翼系统载荷分析、计算流体力学、网格生成技术等研究。
1673-1220(2017)01-008-05
V211.52
A

