数学模型在“种群数量的变化”一节中的应用*

谭　鹃霍　静

（1西南大学附属中学　重庆　400700　2西南大学生命科学学院　重庆　400715）

“模型”是指反应原型本质属性的物质形式或思维形式的类似物，是在特定的科学研究目的和假设条件下进行，能够重新反映原型的结构、功能和过程等［1］。其中，用于表达生命活动规律的计算公式、函数式、曲线图，以及由实验数据绘制成的柱形图、饼状图等称之为数学模型，属于学科交叉的通用概念［2］。构建数学模型的基础是数学方法，对于学生来说具有一定的难度。其构建过程不仅需要学生掌握其一般步骤，还需要学生能够领悟并归纳出其规律［3］。

本文以数学模型构建方法为指导，以“种群数量的变化”一节的教学设计为例，论述在教学中如何引导学生构建数学模型解决问题的具体方法。为数学模型在中学生物学教学中的应用提供参考案例。

1　“数学模型”教学案例展示

教师展示一幅实验室培养的大肠杆菌所形成的菌落图，通过提问：“从生命系统的结构层次上讲，培养皿中的大肠杆菌菌落应该属于哪一个层次？”（学生：属于种群）。引导学生参与到研究该种群数量变化的情境中。

大肠杆菌通过二分裂繁殖，每20 min繁殖一代，现以一个“大肠杆菌的种群”作为大家的研究对象。

1.1提出问题用什么办法可以描述大肠杆菌种群随着时间的增加数量发生变化的情况？（学生根据已有的数学知识，可能会想到计数、曲线图、公式等方法，但具体怎样操作学生并不知道）。进一步引导学生思考：

①首先，可以用最简单的方法，先从众多的大肠杆菌种群中，观察1个大肠杆菌，随着时间的增加计数大肠杆菌数量的变化情况。

②怎样才能规范而又准确地记录对应时间下大肠杆菌的种群数目？（学生会想到列表）

③如何设计表格？（学生会想到至少包含时间、分裂代数、种群数量等项目，设计并完成表1）

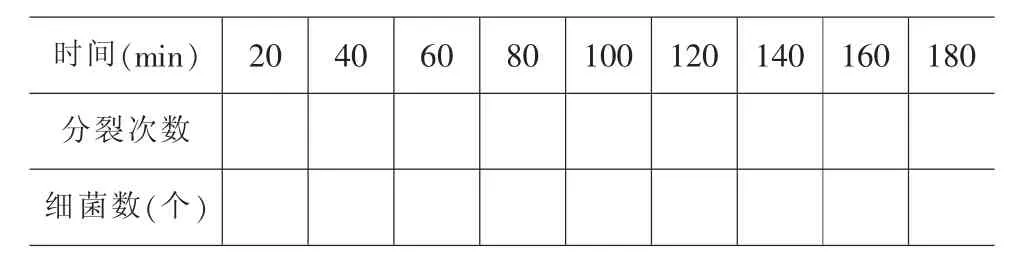
表1　1个大肠杆菌产生的后代在不同时间的数量

1.2作出假设学生完成表1后，教师抓住时机，引导学生作出假设：在营养和生存空间没有限制的情况下，1个大肠杆菌每20 min分裂繁殖一代，在分裂第t次后会繁殖出多少大肠杆菌？

1.3构建模型学生利用数学递推法写出分裂t次后细菌数目Nt的计算公式，即Nt=2t。在此基础上提出数学模型的概念，即用于描述一个系统或它的性质的数学形式叫做数学模型，例如用于反映大肠杆菌数目变化的公式，就属于数学模型。

1.4修正模型一般情况下，初次建立的数学模型可能无法准确反映原型的本质属性和规律，需要对模型进行检验和修正。例如可以这样引导学生对模型进行修正：

①在公式Nt=2t中，“2”代表什么意思？（学生回答：代表大肠杆菌本次分裂产生的个数是上一次的2倍，即增长倍数）。

②如果某种群数量的增长倍数不是2倍，用什么表示？（学生会想到不是所有种群数量都按2倍增长，可以引入一个参数如λ表示增长倍数）。

③在构建模型Nt=2t时，学生作的假设是细菌的初始数目是1个，但是实际状况中细菌的起始数目肯定不止1个，如何修正该模型？（可以假设起始数目为N0）

1.5总结归纳构建数学模型的一般步骤通过以上问题的讨论，学生已经对构建的模型进行了修正，即可以用Nt=N0λt表示理想状态下种群数量的变化。此时，师生可共同及时归纳总结构建数学模型的一般方法：①观察研究对象，提出问题；②提出合理的假设；③用适当的数学形式对事物的性质进行表达；④对模型进行检验或修正。

需要特别指出的是，对于同一个系统或者研究对象而言，只要能够反映原型本质属性或基本规律的模型，都可以用于对研究对象进行描述。例如也可用曲线图反映细菌数目变化的规律。让学生画出大肠杆菌的数量增长曲线，如图1所示：

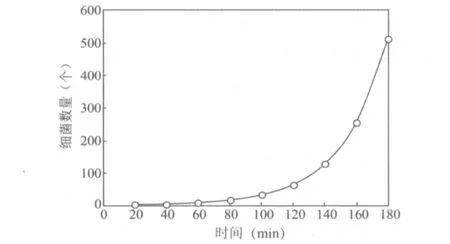
图1　大肠杆菌种群的增长曲线

教师进一步引导学生比较公式和曲线图2种数学形式各自的优点，使学生学会根据实际需求构建适当形式的模型。

1.6模型应用在学生对数学模型有了感性和理性认识之后，进一步用数学模型思想解决具体问题：1959年，一位英国人带了N0只野兔到澳大利亚，如果在食物和空间充裕、气候适宜、没有敌害等条件下，野兔的数量每年以一定的倍数增长，第2年是第1年的λ倍，t年之后野兔的数量是多少？

通过分析，学生构建理想状态下野兔种群增长的数学模型Nt=N0λt。此时，教师可引导学生对公式中各参数的意义、λ的范围等问题进行分析。

追问：是否还有类似于野兔种群增长的这种实例？引出环颈雉的种群数量增长曲线，并总结种群增长的“J”型曲线。

1.7模型拓展师生讨论种群的“J”型增长数学模型的条件、特点之后，引导学生进一步思考：

①自然状态与理想状态的差异及对种群产生的影响；

②修正“J”型曲线，尝试构建自然状态下种群数量增长的曲线模型。

通过这2个问题，引出高斯“大草履虫种群增长”的实验，并完成种群增长的“S”型曲线及其相关问题的学习。

在学生完成了种群增长的2种模型之后，引导学生解决例如灭鼠、鱼类捕捞等种群增长相关的实际问题。

2　教学反思

《高中生物课程标准》关于“种群数量增长”部分的具体内容标准是“通过探究培养液中酵母种群数量的动态变化，尝试建立数学模型解释种群的数量变动”。显然，引导学生用数学方法解释生命现象，揭示生命活动规律是构建数学模型的着眼点，避免离开生物学讨论数学的倾向。本教学案例展示的具体构建数学模型的过程，就是从具体的生物现象或规律出发，建立抽象的数学模型，又将抽象的数学模型应用于新的问题和情境中，对具体的生物学现象或规律作出解释，并且在应用中拓展和完善模型。

除本节讨论的教学案例外，在中学生物学教学中涉及到的数学模型还有很多。例如，有丝分裂和减数分裂过程中染色体、染色单体及DNA数量的变化规律；酶的活性变化曲线；微生物生长曲线；种群密度计算公式、组成细胞的化学元素饼状图、能量金字塔；呼吸过程中随氧气的浓度增加ATP、CO2的变化曲线；光合作用中随光照强度、温度、CO2等条件的变化光合作用强度的变化曲线等。在教学过程中，教师可选择一些数学模型让学生构建。

实践表明通过构建系列数学模型，学生不仅掌握了构建数学模型的方法，还体验由具体到抽象的思维转化过程，学会从现象中揭示本质和规律，用严密的思维分析问题、解决问题［4］。

［1］谭永平.高中生物学新课程中的模型、模型方法及模型建构.生物学教学，2009,34(1)：10.

［2］美国科学促进协会.面向全体美国人的科学.中国教学技术协会，译.北京：科学普及出版社，2001.

［3］周雪峰.生物学教学中模型构建及应用.生物学教学,2010,35(2)：31.

［4］薛进.模型构建方法在生物教学中应用例析.佳木斯教育学院学报,2012（11）：121.