Two-Stage Resource Allocation Scheme for Three-Tier Ultra-Dense Network

Junwei Huang, Pengguang Zhou＊, Kai Luo, Zhiming Yang, Gongcheng He

School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

I. INTRODUCTION

Recently, UDN technology in 5G has been developing rapidly, showing two trends [1]: the dramatic increase in data traffic and the rapid expansion of network coverage. A large-number deployment of small power base stations(Picocell Base Station, PBS; Femtocell Base Station, FBS) can effectively improve the network throughput and spectrum efficiency.However, dense and irregular deployment of small power base stations will cause the severe inter-small-cell interference [2].

Wireless resource management can effectively eliminate and coordinate inter Small-Cell interference [3]. For the purpose of managing the UDN resource allocation, a multi-dimensional resource allocation algorithm based on non-cooperative game theory is proposed in [4]. In [5], a kind of asymmetric power level interference coordination mechanism is introduced, based on the technology of intersmall-cell interference coordination in the scene of spectrum sharing in UDN. A power allocation scheme based on channel state and interference awareness is deployed in [6] to improve the system performance.

In order to solve the problem of inter-smallcell interference, the majority of scholars and experts generally divide the small cells into several clusters and apply resource allocation or power optimization algorithm to coordinate the small cell interference [7-12]. A distributed energy-efficient resource allocation scheme based on clustering is proposed in [7], whose performance is verified by system-level sim-ulation. Considering the complexity of cooperation and backhaul overhead, Reference[8] proposes a clustering-based interference management mechanism, which firstly divides small base stations into different clusters and eliminates intra-cluster and inter-cluster interference based on collaboration. In [9], a graphbased clustering resource allocation (GCRA)is proposed. The main idea of GCRA is that all the base stations are divided into independent clusters based on complete staining algorithm in graph theory and then eliminate inter-smallcell interference by allocating orthogonal spectrum resource for different clusters. In[10], a semi-distributed interference management mechanism based on Femtocell clustering and resource allocation is introduced. Reference [11] mainly studies the cluster-based resource allocation issues in UDN, and proposes a CTRM (cluster-based two-stage resource management) algorithm to improve system spectrum efficiency and throughput.In ultra-dense deployment of Femtocell network, a user-oriented graph based frequency allocation (UGFA) algorithm based on graph theory is performed in [12] to increase the frequency reuse rate and network throughput.In [13], in order to fit the present file demand,cache update, and file transmission without a centralized information collection controller, a distributed video distribution scheme (DVDS)in D2D is proposed. Reference [14] researches the optimal computing manner under the scene of Media Cloud and the author of [14]proves that the optimal diversity configuration is DL-2 diversity.

However, the algorithms mentioned above didn’t take the users’ fairness and satisfaction into account. Moreover, most of them insufficiently studied the sophisticated scene and network architecture in UDN, which merely paid attention to the inter-small-cell interference coordination and resource allocation among FBSs. Aiming at the problems above,in this paper, we synthetically consider the cross-layer interference and co-layer interference under three-layer network (Macrocell-Picocell-Femtocell) in UDN and put forward a Logarithmic-function [15] and K-means-clustering-based Two-stages Resource Allocation(LKTRA) scheme. The LKTRA program is divided into two parts: in the first part, a two-level sub-channel allocation algorithm for MBS (Macrocell Base Station) and PBSs and an optimal power control method are performed to guarantee sub-channels allocation of MBS and PBSs. In other words, we use the characteristics of non-negative variables of logarithmic function to ensure the requirements of users’ minimum SINR (signal to interference plus noise ratio) and optimize deeply the transmission power of PBSs; in the second part, firstly, an improved K-means clustering algorithm is presented in the process of FBSs clustering, which can retain the fast convergence speed and avoid appearing local optimal conditions after iterations. Then we calculate the priority of different FBSs clusters. Finally, we propose an efficient sub-channel allocation algorithm based on the priority of FBSs clusters to satisfy the resource requirements of FBSs. System-level simulation results show that the proposed LKTRA scheme can effectively coordinate the inter-small-cell interference, orderly assign sub-channel resources and promote the system performance.

In this paper, a resource allocation scheme based on logarithmic function and improved K-means clustering in the three-tier network architecture for UDN is proposed.

II. SYSTEM MODEL

2.1 The description of system model

In this paper, we consider a real block area as the system model, which can be approximately defined as a 400m400m× square area A0consisting of MBS, PBSs and FBSs. The detailed architecture of area A0is shown in figure 1.

Fig. 1 System model

We consider a downlink OFMDA interference system in UDN, which is divided into three tiers: the first tier is MBS network layer.MBS is located in the center of the system model and we define that all of the user equipments (UEs) in circular coverage areaA1with the center point (MBS) and a radius of 50m-100m should access to MBS for service;the second tier is PBS network layer. Due to the wide coverage of PBSs, PBSs are suitable for the vast environment. Besides, PBS can substitute FBS under certain circumstance,avoiding serious interference problems caused by dense and irregular deployment of FBSs.So in the limited region A2=A0-A1, a small number of PBSs are mainly deployed in large shopping malls and offi ce buildings; the third tier is FBS network layer. A large number of FBSs are intensively distributed in residential areas and edge position of area A0, mainly in order to improve the edge-cell UEs’ data transmission rate and overall system throughput. In order to achieve the green communication as much as possible, we also consider the sleeping strategy of PBSs and FBSs [16].

All of the UEs are randomly deployed in area A0and the UEs which are located in area A1belong to MUEs (Macrocell User Equipments). For simplicity, we decide that the rest of UEs can choose the nearest service base station from their location. The set of MUEs can be presented as UM, where M={1,2,…,mu}is the number of MUE within area A1, muis the ID number of specific MUE; the set of PUEs (Picocell User Equipments) can be presented as UP, where P={1,2,…,mp} is the number of PUE within areaA2, puis the ID number of specific PUE; the set of FUEs(Femtocell User Equipments) can be presented as UF, where F={1,2,…,mf} is the number of FUE within area A2, fuis the ID number of specific MUE. The set of sub-channels can be indicated as N, where N={1,2,…,n}, n is the ID number of specific sub-channel.

2.2 Interference analysis

In this paper, we merely consider the downlink interference including the cross-layer interference and co-layer interference under the three-tier network. The network interferences include the interference of MBS towards PBSs and FBSs, the interference of PBSs towards FBSs, and the interference among PBSs and the interference among FBSs. Assuming that MBS, each PBS and FBS can greatly obtain the CSI (channel state information) of their service UEs.

2.2.1 MBS interference analysis

We use subscript m in equation to represent the relevant Definition about MBS. The SINRserved by MBS j on themchannelncan be written as:

2.2.2 PBS interference analysis

2.2.3 FBS interference analysis

ifserved by FBS jfon the channel n can be presented as:

where Nfrepresents the maximum number of FBSs.

III. RESOURCE ALLOCATION FOR MBS AND PBS

In section 2.2, we introduce PBSs into our UDN network system, which lead to a more complex interference environment, especially in the coverage area of FBSs. So we first assign resource for MBS and PBSs. After that,we separately analyze the resource allocation of FBSs, and the concrete allocation algorithm is given in section IV. In this section, we firstly apply a sub-channels algorithm for meet the requirements of MBS and PBS based on the optimal system throughput. Then we design a power control model for PBS in order to optimize the transmission power for PBS. In other words, we consider the diminution of interference while the process of allocating the sub-channels resource.

3.1 Sub-channel allocation for MBS and PBS

In this paper, we consider the minimum network throughput as the basic requirements and a two-level sub-channel allocation algorithm for MBS and PBSs is deployed, which can satisfy the requirement of minimum network throughput and efficiently assign sub-channels for MBS and PBSs at the same time. The system throughput of MBS and PBS can be respectively expressed as:

We respectively define the minimum system throughput of MBS and PBS as CM,minand CP,min, and CP,maxdonates the maximum system throughput of PBS.

3.2 Power control for PBSs

3.2.1 Power control model

In UDN, the total amount and transmission rate of data service are dramatically increasing. On the basis of the lowest SINR of UEs,it’s truly efficient to improve the UEs’ experience by trying to enhance the UEs’ SINR. We suppose thatis the minimum SINR ofPUE puserving by PBS pj and ℙ is the set of PBS, so the SINR γpjp,uof PUE puneed to meet:

Algorithm 1: Two-level sub-channel allocation algorithm

On the condition of (14), a power control algorithm based on Logarithmic Function is introduced and utility function of PUE pucan be presented as:

The specific utility function based on Logarithmic Function can presented as:

3.2.2 Power iteration

Let equation (190)=:

We can see that every PBS can reach the Nash Equilibrium on the condition of(20),which can guarantee the QoS (Quality of Service) of PBSs.

We can express the transmission power Ppj,puof PBS pj as:

According to Newton-Raphson Method, the power iteration equation can be expressed as:

The transmission power of PBS pj under(1)ki+ iterations is:

IV. RESOURCE ALLOCATION FOR FBSs

In this section, we deal with the resource allocation for FBSs in the third tier network. The improved K-means [17] clustering algorithm with faster convergence speed and lower complexity is used for the clustering of FBSs.Then we calculate the clusters’ priority according to the priority of every FBS in different clusters. In addition, the sub-channels are assigned to FBSs in the order of priority level.Besides, we define that certain clusters can reuse the spectrum resources with those clusters without mutual interference.

4.1 Modified K-means algorithm

4.1.1 The details of modified K-means algorithm

Traditional K-means algorithm needs to select the initial cluster centers before clustering,and it may lead to the increase of clustering iterations and partial optimization rather than global optimization. At the same time, different initial cluster centers may appear different clustering results, which make the traditional K-means clustering algorithm much unstable[19]. Based on the above problems, we use a modified K-means algorithm to cluster the FBSs under the MBS coverage and select the CHs (Cluster Heads) of FBSs cluster for distributed interference management and resource allocation.

We propose a K-means-based FBSs Clustering (KFC) algorithm: firstly, according to the regional deployment of FBSs, we use cosine angle method to approximately calculate the distance between each pair of FBSs; then maximum distance algorithm is applied to compute the set initial CHs to prevent KFC algorithm to emerge the condition of partial optimization; finally, input the information of CHs into K-means to calculate the final CHs and clustering results. The detailed step of modified K-means algorithm is shown in algorithm 2:

4.1.2 The complexity and convergence analysis

In order to demonstrate the advantages of KFC algorithm in the complexity and convergence,we make a series of comparisons between the traditional k-mean algorithm and the k-medoid[17] algorithm under the system model in Section II.

In complexity, K-mean algorithm randomly chooses the value of K, so it has the minimum complexity, which can be denoted as O(KNft), where K, Nfand t is the number of CHs, FBSs and iterations, respectively. The KFC algorithm adds certain steps of calculating the K on the basis of K-mean so that the complexity can be divided into two parts: the first part is the K calculation complexity O((K-1)Nf); the second part is the complexity of traditional K-mean algorithm O(KNft), so the overall complexity of KFC can be written as O((K-1)Nf+KNft ). The algorithm complexity of K-medoid is O().From the analysis above, we can see that the complexity of KFC is slightly higher than k-mean but it is far lower than the K-medoid.

In convergence speed, we set different FBSs number in system model, and judge the convergence performance of different al-gorithms according to the execution time of clustering. The clustering execution times of K-mean, KFC, and K-medoid are compared in figure 2. With the increase of the number of FBS, the time required for clustering significantly increased, but the KFC algorithm reveals the best performance when FBS number is 0-120. Therefore, we can conclude that the KFC algorithm is more suitable for the system model and theoretical analysis.

Algorithm 2: KFC algorithm

4.2 The priority of clusters

Considering the UEs’ fairness and satisfaction without loss of generality, we study a variety of factors that affect the priority of resource allocation. In this section, the priority of each cluster is calculated according to the load intension, the interference degree and the waiting time of data to be transmitted of every FBS in different cluster. Generally speaking,the bigger FBSs load intensity, the stronger intensity of interference and the longer queue waiting time, the specific FBSs has the higher priority to receive spectrum resources.

1) We estimate the system load intension of FBS jfby the transmission rate of jf. Assume that the number of FUEs access to FBS jfis njf, and the load Fjfof FBS jfcan be expressed as:

Fig. 2 Execution time

2) According to the system model, the interference degree Ijfof FBS jfcan be written as:

3) Assume that the resource requirement time of FBS jfis Treqand resource acceptance time of FBS jfis Trec, so we can summarize the waiting time of data to be transmitted of FBSs as:

Based on the above analysis, we define the priority of cluster in the system as the ratio of three weighted values of the FBS in same cluster to these of all FBS:

4.3 Prior resource allocation

In this paper, the significance [21] of the resource allocation is to assign the orthogonal sub-channels for FBSs in the cluster, and a few clusters can reuse the spectrum resources with those clusters without interference. In order to reduce the interference among FBSs and promote FUEs’ QoS, we propose a sub-channel allocation algorithm based on the priority and the minimum requirement of sub-channel numbers of FBSs cluster. Prior sub-channel allocation algorithm is summarized as Algorithm 3:

V. SIMULATION RESULTS AND DATA ANALYSIS

In this section, we use the MATLAB R2009a simulation platform to verify the proposed LKTRA scheme in complex UDN architecture, examining the degree of optimization about several performance indices, such as interference coordination, system throughput,spectrum efficiency and UEs’ satisfaction and fairness. We consider the Rayleigh fading channel model between the small base station and the UEs [7], and the specific simulation parameters are shown in table 1. In order to reflect the feasibility of the LKTRA scheme,we compare LKTRA scheme with PANPG algorithm [4] and UGFA algorithm [12]. In addition, we use Random Resource Allocation(RRA) algorithm as performance reference.

In this paper, the improved-K-means-based FBSs clustering results can be seen in figure 3 which includes six clusters consisting of 90 FBSs under the coverage area A2. In figure 3,six bold boxes represent the selected CHs and different colors denote the different clusters including the cluster members which tightly embrace their own CH. Besides, the central triangle represents MBS and the external circle is the representation of area A1in system model. In addition, the size of the cluster is greatly controlled. Therefore, the K-meansbased FBSs clustering algorithm proposed in this paper can be used as the premise of priority calculation and resource allocation.

Figure 4 depicts the cumulative distribution function (CDF) of the average system throughput about the four algorithms. It can be seen clearly that the system throughput is significantly higher than that of the other three algorithms. That is because the LKTRA algorithm applies PBSs into the system model, avoiding the dense deployment of a large number of FBSs which lead to serious interference; then the logarithm function model for PBSs poweroptimization and control is performed to reduce the inter-small-cell interference; in the end, vast number of FBSs are divided into different clusters and we calculate the clusters’ priority in order to assign sub-channels with better channel gain to the cluster of high priority, which can effectively eliminate the interference among FBSs and further enhance the system throughput. In addition, RANPG algorithm mainly focuses on the optimization of transmission power without considering the optimization problem of sub-channels allocation; UGFA algorithm assign resource for small cell in proportion without referring to the power optimization, therefore, the intersmall-cell interference cannot effectively eliminate as well.

Algorithm 3: Prior sub-channel allocation algorithm

Table I Simulation parameters

Fig. 3 Clustering results

Fig. 4 Average system throughput

Fig. 5 Average system spectrum efficiency

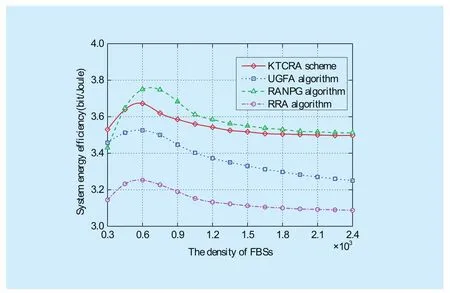
Fig. 6 System energy efficiency

The CDF of the average system spectrum efficiency is shown in figure 5. RRA algorithm plays a role in performance baseline. And compared with RRA, the system spectrum efficiency of three other algorithms is absolutely improved. In UFGA algorithm, the same number of resource blocks is assigned for each cluster. If the number of UEs in a cluster is relatively small, it is inevitable to cause the waste of spectrum resources. LKTRA scheme is able to outperform RANPG algorithm in spectrum efficiency mainly can be summarized as follows: 1) LKTRA scheme specializes in eliminating interference among various small power base stations; 2) LKTRA scheme considers the mechanism of frequency reuse at the same time. Namely the distant PBSs or FBSs cluster without mutual interference can multiplex the same frequency spectrum for saving the infrequent spectrum resource in UDN system.

Figure 6 describes the energy efficiency of the four algorithms under different density of FBSs. It appears that the system energy efficiency of LKTRA scheme and RANPG algorithm respectively reaches optimal point at density of FBSs in 0.510×3and 0.710×3. It is inevitable for the increasing system energy consumption of LKTRA scheme due to the deployment of a certain number of PBSs in order to enhance the system throughput and spec-trum efficiency. But system energy efficiency of LKTRA scheme and RANPG algorithm shows a smooth trend at 1.210×3of FBSs density. UGFA algorithm merely takes the power allocation into account without mentioning energy-saving scheme. Besides, RRA algorithm without any energy saving scheme has the worst performance in terms of system energy efficiency.

The UEs’ satisfaction [12] under different FBSs density is displayed in figure 7, which reflects the relationship between the actual transmission rate and the minimum transmission rate. The UEs’ satisfaction of RANPG algorithm and the LKTRA scheme is enjoyed a high level because these two algorithms perform well in the inter-small-cell interference management and maximum of the UEs’ actual data transmission rate. Besides,LKTRA scheme assigns the different quality of sub-channels for FBSs clusters based on its priority, which further promotes the UEs’satisfaction. UGFA algorithm does not give a practical solution scheme in the matter of interference management, resulting in out-ofcontrol inter-small-cell interference and the lower UEs’ data transmission rate.

In this paper, we use the Jain fairness index[20] to judge the fairness of different strategies. Figure 8 plots the UEs’ fairness of the four algorithms under different FBSs density,and the fairness of FUEs among different algorithms is mainly discussed in this paper.Compared with other algorithms, LKTRA scheme has more advantages in the aspect of UEs’ fairness. The FBSs clustering algorithm based on improved K-means with the better convergence speed is designed, which demonstrates the great performance for the clustering process. The QoS and resource requirement of members in different clusters can be tremendously satisfied by LKTRA scheme. As for UGFA and RANPG algorithm, the fairness of FUEs is relatively lower than that of LKTRA scheme because both of them merely consider the interference intensity among small cells.

Fig. 7 UEs’ satisfaction

Fig. 8 UEs’ fairness

VI. CONCLUSION

In this paper, we innovatively propose a resource allocation scheme based on logarithmic function and improved K-means clustering in the three-tier network architecture for UDN.For the tier of MBS and PBS, a two-level sub-channel allocation algorithm is performed and the optimal power model based on logarithmic function is established to ensure the PUEs’ minimum SINR requirements; for FBS tier, an improved K-means clustering algorithm is used in the process of FBSs clustering for distributed interference management.Moreover, the priority of every cluster is calculated for a prior sub-channel allocation algorithm which meets the different resource requirement of FUEs. The simulation results show that the LKTRA scheme can effectively improve power optimization of small power stations, reduce the inter-small-cell interference, and significantly improve the system throughput and spectrum efficiency.

[1] S.Z Shan, F. Qin, B. Hu, et al, “User-centric ultra-dense networks for 5G: challenges, methodologies and directions,” IEEE Wireless Communications, vol.23, no.2, pp.78-85, April, 2016.

[2] M. KAMEL, W. Hamouda, A. Youssef, “Ultra-dense networks: a survey,” IEEE Communications Surveys & Tutorials, vol.18, no.4, pp.2522-2545, Fourth quarter, 2016.

[3] X.R Zhu and W.R Zhu, “Interference coordination-based cell clustering and power allocation algorithm in dense small cell networks,” Journal of Electronics & Information Technology, vol.38,no.5, pp.1172-1176, May, 2016.

[4] Z. Wang, X.R Zhu, X. Bao, et al, “A novel resource allocation method in ultra-dense network based on noncooperation game theory,”China Communication, vol.13, no.10, pp.169-180, October, 2016.

[5] Q.L Yu, J. Wang, X.M Yang, et al, “Inter-operator interference coordination for co-primary spectrum sharing in UDN,” China Communications,vol.12, no.s1, pp.104-112, December, 2015.

[6] Y.H Gao, L. Chen, X. Zhang, et al, “Enhanced power allocation scheme in ultra-dense small cell network,” China Communications, vol.13,no.2, pp.21-29, February, 2016.

[7] L. Liang, W. Wang, Y.J Jia, et al, “A cluster-based energy-efficient resource management scheme for ultra-dense networks,” IEEE Access, vol.4,pp.6823-6832, September, 2016.

[8] S.Y Tang, C.Y Sun, J.X Zhang, et al, “Interference management based on cell clustering in ultra-highly dense small cell networks,” Proc.International Conference on Information and Communications Technologies, March, 2015.

[9] Q. Zhang, X.N Zhu, L.J Wu, et al, “A coloring-based resource allocation for OFDMA femtocell networks,” Proc. IEEE Wireless Communications and Networking Conference (WCNA),April , 2013.

[10] A. Abdelnasser, E. Hossain, and I.K Dong, “Clustering and resource allocation for dense femtocells in a two-tier cellular OFDMA network,”IEEE Transactions on Wireless Communications,vol.13, no.3, pp.1628-1641, January, 2014.

[11] R. Wei, Y. Wang and Y. Zhang, “A two-stage cluster-based resource management scheme in ultra-dense networks,” Proc. IEEE/CIC International Conference on Communications (ICCC),October, 2014.

[12] Z.R Luan, H. Qu, J.H Zhao, et al, “User-oriented graph based frequency allocation algorithm for densely deployed femtocell network,” China Communications, vol.10, no.12, pp.57-65, January, 2013.

[13] L. Zhou, “Mobile Device-to-Device video distribution: theory and application,” ACM Transactions on Multimedia Computing, Communications and Applications, vol. 12, no.3, pp. 1253-1271, March, 2015.

[14] L. Zhou, “Specific versus diverse computing in media cloud,” IEEE Transactions on Circuits &Systems for Video Technology, vol. 25, no. 12,pp. 1888-1899, Dec. 2015.

[15] R.D Yates, “A framework for uplink power control in cellular radio systems,” IEEE Journal on Selected Areas in Communications, vol.13, no.7,pp.1341-1347, August, 1995.

[16] C. Zhang, J.C Fan, and X.M Luo, “Spectrum and energy efficiency analysis of ultra dense network with sleep,” Proc.2016 8th IEEE International Conference on Communication Software andNetworks (ICCSN), October, 2016.

[17] H.M Ye, H. Lv, and Q.T Sun, “An improved semi-supervised K-Means clustering algorithm,”Proc. 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, May, 2016.

[18] S. Shah, M. Singh, “Comparison of a time effi-cient modified K-mean algorithm with K-Mean and K-Medoid algorithm,” Proc. International Conference on Communication Systems and Network Technologies, May, 2012.

[19] D.H Zhai, J. Yu, F. Gao, et al, “K-means text clustering algorithm based on initial cluster centers selection according to maximum distance,”Application Research of Computers, vol.31, no.3,pp.713-715, March, 2014.

[20] A. HATOUM, R. LANGAR, N. AITSAADI, et al,“Cluster-based resource management in OFDMA femtocell networks with QoS guarantees,”IEEE Transactions on Vehicular Technology,vol.63, no.5, pp.2378-2391, November, 2014.

[21] H.B Zhang, L.X Mu, S.X Chen, et al, “A cluster-based resource allocation in a two-tier OFDMA femtocell networks,” Proc. Journal of Electronics & Information Technology, vol.38,no.2, pp.262-268, February, 2016.