A Fast and Memory-Efficient Approach to NDN Name Lookup
Dacheng He, Dafang Zhang,*, Ke Xu, Kun Huang, Yanbiao Li College Computer Science and Electronic Engineering, Hunan University, Hunan 4008, China
2 Institute of Computing Technology, Chinese Academy of Sciences, Beijing, China
* The corresponding author, email: dfzhang@hnu.edu.cn
I. INTRODUCTION
With the continuous growing of network techniques and applications, the Internet has far exceeded expectations. Its host-based communication model, based on initial assumptions,has thus suffered from a series of issues due to today’s requirements. To address the weakness of current Internet, NDN [1] has been proposed as a new architecture for future Internet.Its content-based communication model shift the major focus from where (the hosts and their addresses) to what (the data contents and their names). As depicted in figure 1, the NDN communication is consumer-driven [3].It starts by the users (or applications) for their requests of named data, which are forwarded as interest packets by NDN nodes. Then, the node (a router or a content provider), that receives an interest packet and exactly has its requested data, responds it with data packets.For each NDN node, three Tables are involved in forwarding packets: (1) The Content Store(CS) buffers received data according to some cache policies [4]. (2) The Pending Interest Table (PIT) records the incoming face (s)1It is just the interface of NDN node.of all forwarding interest packets, associated with the names of their requesting content. (3) The Forwarding Information Base (FIB) plays the similar role as the traditional IP FIB, but what stored in it are name prefixes and their corresponding lists of output face(s).

Fig. 1 NDN communication example
More specifically, when an interest packet arrives, its content name is firstly used to perform Exact String Matching (ESM) in CS2If the content name gets matched in CS, it means the requesting data is already buffered in this node and can be returned as data packet immediately.and PIT3If the content name gets matched in PIT, it means the request of its requesting data has been handled, and previous interest packets are still waiting for responds. So,the incoming face of this interest packet should also be appended to the waiting list.in order. If both fail, that name is used to perform Longest Name Prefix Matching(LNPM) in the FIB to find the output face(s).By contrast, when a data packet arrives, if its content should be cached, its name is inserted into CS. Besides, its name should be looked up in PIT to find out the waiting list, from which a face is then popped out as the output face of this packet. In memory, these logic Tables can be organized as a single one, that is referred to as Name Table in the rest of this paper, with each Table entry recording its own type in the mixed structure [12]. Besides, this paper focuses only on the LNPM of name Tables4Since the LNPM can naturally tell whether the ESM succeeds. And ESM is just the LNPM as long as it succeeds. In this view, only one LNPM in the name Table is required for each packet.The type and associated information of the matched entry is then used to determine the proper operation.. Even though, designing a fast and scalable forwarding engine for NDN remains challenging [10, 11, 12].
Firstly, the name prefixes in NDN are hierarchical strings (e.g.com/google/news/)with longer lengths than IP prefixes, and their lengths are variable and without externally imposed upper bound. Besides, each name prefix is composed of a sequence of components delimited by some separator (such as /), and the LNPM inner any component is invalid.For instance, com/google/news/ can match com/google/ but can not match com/google/new/. While for IP lookup, the LNPM can be achieved in any bit position. In fact, name lookup is far more complex than IP lookup,and is, thus, harder to meet the ever-increasing link speed5.
Besides, in comparison with today’s IP routing Tables that hold up to 400 - 500 K entries, NDN name Tables could be multiple orders of magnitude larger [2, 9]. There must be great pressure to handle so large-scale Tables without novel compressing techniques,especially when accelerating name lookup by some special devices, such as GPUs, that have scarcer device memory.
To address these challenges, researchers have made great efforts. First of all, the NDN proposal [12] presents a fast name lookup approach that is based on the Ternary Content Addressable Memory (TCAM). But it only handles relatively short FIB entries, and the high-cost update and high power consumption of TCAM restricts its application for largescale Tables. Besides, trie-based approaches[8, 9] can achieve a good tradeoff between comprehensive requirements due to novel structure designs. Moreover, they can also benefit a great computing power from GPU’s massive parallelism to accelerate name lookup speed [7,9]. But their unstable lookup speed and complicated structures restrict their use in practice.
On the other hand, several hash-based solutions have been proposed to provide fast name lookup with very simple logic, by utilizing bloom filters [6] and effective hash functions[13,5]. Although calculating hash values can be very fast, performing prefix matching on names will result in many times of hash computing and verification. To address such a potential performance issue, Binary Search of Hash Table algorithm (BSH) has been proposed [14]. Given a name of n components,BSH starts length-detecting at n/2, namely searching the prefix made up by its first n/2 components in the hash Table corresponding to this length. If the searching tells a match, then the next detecting length will be 3n/4. Otherwise, it will be reduced to n/4. To ensure such a binary search path correct, a real prefix in the FIB will produce one or more virtual prefixes that located along the correct searching path for it. By this means, BSH can perform LNPM very fast without any backtracking, but additional memory costs resulted by those virtual prefixes will be another issue, especially when considering large-scale Tables.
In this paper, to eliminate redundant memory costs to improve memory efficiency,we propose to use bloom filter to verify the presence of a prefix of the detecting length of the given name. The key contributions of our
work are summarized as follows.
● We point out a potential issue the binary search solution with experimental results and make this our research motivation.
● We make a deep study on the binary search strategy and then propose a Bloom-filter assisted Binary Search (BSS) algorithm to ensure correct searching paths without backtrack nor redundant memory consumptions.
● We conduct a series of evaluation experi
ments to demonstrate our superiorities.
The rest of this paper is organized as follows. Section II introduces the existing binary search algorithm. Starting from a motivation example, section III proposes our solution in detail. Then sections IV and V discuss the system design and our evaluation experiments. At last, section VI concludes the whole paper.
II. THE BACKGROUND ON BINARY SEARCH OF HASH Table S
As soon as a string match occurs, the LNPM algorithm finishes matching. Therefore, the lookup times of LNPM is O(n), where n is the number of name component. Because the BSH algorithm [14] reduces lookup times from O(n) to O(log n), it can achieve quick lookup and high throughput by using the binary search strategy.
Now we compare the LNPM algorithm with the BSH algorithm through an example.The FIB is shown as the left of figure 2, and the number of longest name prefix components is 7. Therefore, we build 7 hash Tables to store the name prefix. HTnmeans this hash Table just stores the name prefixes that contains n components. Suppose the target name a/c/b/d/e/f/g/x, with its component number is longer than 7. The process of LNPM is as follows.Firstly, lookup the first seven components a/c/b/d/e/f/g in HT7, it fails. Then lookup a/c/b/d/e/f in HT6, it also fails. It finishes until the 7thlookup because name prefix a is stored in HT1.
However, BSH may not lookup in hash Tables so many times. Generally, binary search employs binary tree to operate. BSH organized the hash Tables like a binary tree structure that is shown in the right of figure 2. Consequently,HT4becomes the root node. First of all, lookup the first four components a/c/b/d in HT4.Then lookup the left subtree if it fails, otherwise lookup the right subtree. BSH obtains the result of hash lookup only 3 times as shown in the dotted lines with an arrow in the right of figure 2.
After lookup in hash Tables, a string match is necessary to confirm whether the result of hash lookup is correct. BSH provides two strategies for string match. The first is making a string match after each hash lookup ends.The other is making a string match after all the hash lookup finishes. Obviously, the second strategy needs backtracking in some situation although it may save the time in most case.One situation is that there is a successful lookup in the hash Table while the string match fails.
In fact, BSH algorithm in name prefix lookup brings an inherent problem. Again in figure 2, suppose that the target name is changed to a/b/c/d/e/f/g/x, so the correct result is the name prefix P4that is in the HT7. According to BSH algorithm, the different result prefix P3is obtained nevertheless, as shown in the solid line with an arrow in the right of Fig 2.The reason is that the 6-component sub-prefix of P4is not stored in HT6, leading the path to the left subtree. In order to solve this problem,BSH has to insert the sub-prefix in the higher layer when inserting a name prefix in the lower layer. In the above case, after inserting 7-compnent real name prefix a/b/c/d/e/f/g in HT7, BSH inserts 6-component virtual name prefix a/b/c/d/e/f in HT6. In this way, BSH can lookup rightly.

Fig. 2 Binary search of hash table algorithm
However, this solution makes the memory consumptions of BSH increasing greatly because it inserts too many virtual name prefixes in hash Tables. In order to avoid this, we propose a novel algorithm to ensure correctness of binary search of hash Table. This algorithm has neither additional backtrack costs nor redundant memory consumptions.
III. BLOOM FILTER ASSISTED BINARY SEARCH
In this section, we introduce the Bloom-filter assisted Binary Search (BBS) algorithm in several aspects, such as the motivation, its work process, and a simple evaluation for false positive.
3.1 Observations and motivations
As mentioned before, the BSH is efficient in time consumption by reducing the times of hash lookup, while it needs additional memory consumption to keep the correctness of lookup process.
For further evaluation, some simple experiments are designed. These experiments indicate that BSH reduces the time consumption indeed. Nevertheless, when using the random name prefixes, BSH adds large numbers of virtual nodes. And it becomes even worse along with the larger database. If lookup millions of name prefixes, the number of virtual prefixes is nearly reach 70% of real ones.
Considering this problem, this paper desires a solution to play the similar role of virtual nodes while cutting down the additional memory consumptions.
3.2 Binary search with the help of Bloom filters
Bloom filter is a data structure with low memory consumption but high lookup speed. It is expected to be suitable for our purpose. And in recent years, it is widely used in forwarding Table lookup [15, 16, 17].
This paper proposes a BBS algorithm hence. Instead of storing virtual name prefixes in hash Table directly, BBS stores them in the bloom filters. Therefore, BBS adds the bloom filter for each hash Tables. It is obviously that storing in the bloom filter costs much less memory than in hash Table.
We introduce the BBS algorithm also through an example. FIB is shown in the left of figure 3, and the corresponding tree structure is the right of figure 3. Notice that FIB contains 3 real name prefixes and 2 virtual ones. BBS adds a bloom filter for each hash Table except that is in the bottom. BFnis used to store n-component virtual name prefixes. It means bloom filter BF4and BF6store the virtual name prefix P4and P5respectively.
In this way, the lookup process of BBS is as follows. Suppose that the target name is a/b/c/d/e/f/g/x. According to the BBS, lookup the first four components a/b/c/d in BF4and HT4in turn firstly. It is successful in BF4but fails in HT4. The result means a/b/c/d is not a real name prefix in FIB, but it may be a sub-prefix of one real name prefix in FIB. So it proceeds the right subtree next. After lookup in BF6and HT6, it reaches the HT7where it can obtain the result P3. The process is shown in the dotted lines with an arrow in the right of figure 3.
Depending on different result of lookup,BBS divide it into 3 cases. First, it proceeds right subtree if BBS succeeds in BFn.This means there may be a real name prefix in the longer component hash Tables. Second,it proceeds left subtree if BBS fails in both BFnand HTn. This means there is no matched name prefixes in neither this length hash Table nor the longer component hash Tables.Third, BBS achieve the result only if it fails in BFnbut succeeds in HTn. It means a matched name prefix in the hash Table of current length meanwhile it is impossible to find the matched name prefix in the longer component hash Tables.
In this example, BBS and BSH both have 3 lookup times in hash Tables. However, BBS has extra 2 lookup times in bloom filters. This means BBS uses additional lookup times in bloom filter to reduce the redundant memory computations in BSH. As we all known,bloom filter lookup costs much less than hash lookup. Consequently, BBS is more efficient than BSH in lookup process.

Fig. 3 Bloom-filter assisted binary search algorithm

Algorithm 1: Lookup name prefix in FIB //
3.3 Update algorithm
Update plays an important role in the current Internet. Update process of BBS is similar to its lookup process by binary search. When FIB inserts a new name prefix, it is stored into the corresponding hash Table. After this operation, BBS inserts the virtual name prefix into the specified bloom filters. Moreover, delete action is not supported by the normal bloom filter. The counting bloom filter can finish this job nevertheless.
For instance, the tree structure is identical with figure 3. Suppose that inserting a new name prefix P6: a/b/c. BBS inserts P6into 3-component hash Table HT3first, and inserts P3’: a/b into 2-component bloom filter BF2next. Now delete the prefix P2:a/b/c/d/e, lookup P2in the 7-component hash Table HT7by binary search and delete its information.
3.4 False positive analyzing
BBS algorithm choses murmur hash because of its high balance and low collision for dealing with the large-scale data. Each bloom filter uses 3 murmur hashes to make the element confirm the position. Bloom filter has false positive, and the calculation formula isfalse positive rate, k is hash time, n is the number of elements, and m is the number of bits. Therefore, when random name prefixes reach million, make m =10n, f is nearly 8.12 * 10-7. It means lookup 1 million prefix names may meet 0.8 time false positive. This is obviously acceptable.
IV. SYSTEM IMPLEMENTATION
In this section, we describe the implement of BBS. We focus on its hash design and the organization of data structure.
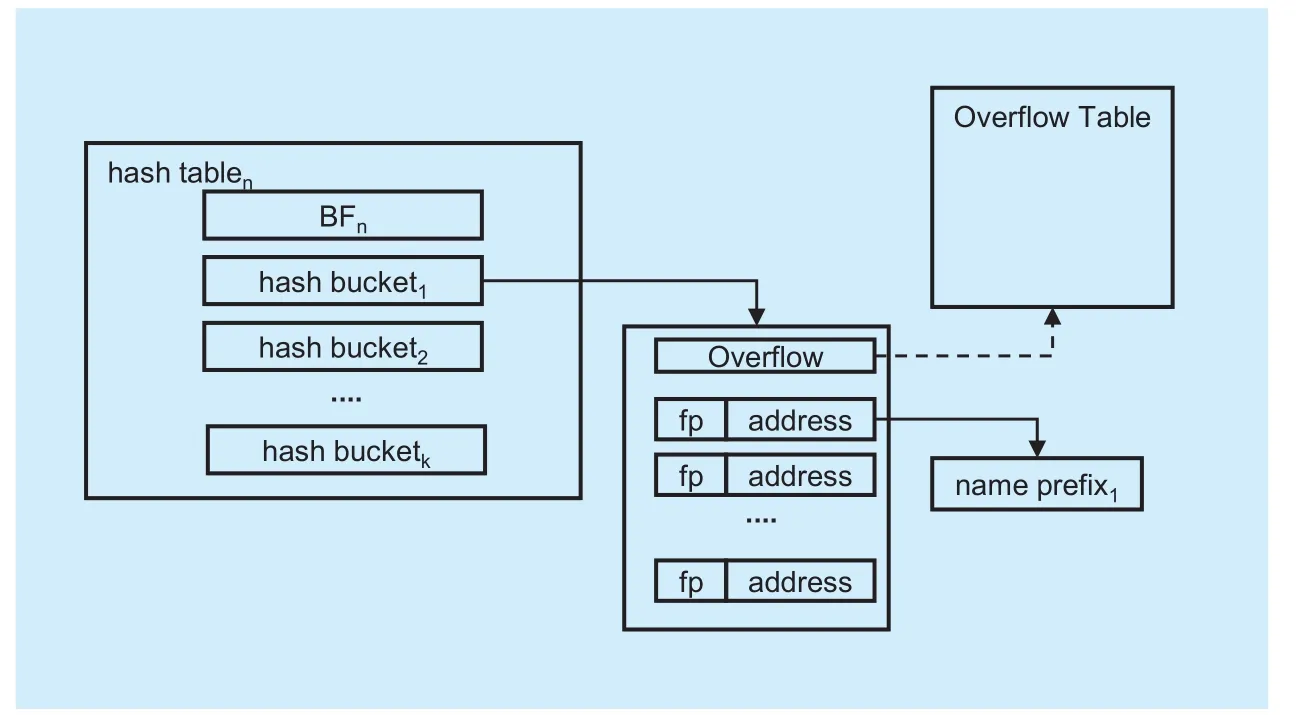
Fig. 4 Hash Table structure in BBS
Different from IP lookup, the name prefixes in NDN do not have a definite limits. Since fingerprint-based hash Table can decrease the memory consumptions greatly, it is widely used in recent works. BBS also uses it to store the name prefixes. The basic data structure in BBS is hash entry. Each hash entry records two information. One is the fingerprint information of name prefix and the other is the address information of the complete name string.Several hash entries form a hash bucket.
Hash Table structure in BBS is shown in figure 4. There are 7 hash entries in one hash bucket, and n/3 hash buckets in a hash Table,n is the number of current length-component name prefixes. The name prefixes are in the same hash bucket if they have the same fingerprint. And they are also in same hash Table if their number of component is the same.Besides several hash buckets, a hash Table has a bloom filter to record the virtual name prefixes. The size of bloom filter is changed with the total number of current length-component name prefixes. The dynamic setting makes the memory used efficiently. There is 1 bit in each hash bucket to record whether it is overflow. If overflow happens, the next hash entry in this hash bucket should be stored in the extra hash bucket. In order to record this information,BBS maintains a Two-dimensional Table.
V. EVALUATION EXPERIMENTS
This Section evaluates BBS algorithm in case of time consumptions and memory consumptions through some simulation experiments.Besides, BSH and other methods are used as contrast.
5.1 Experiment environment
These experiments run on the server of our laboratory. The operating system is Ubuntu 16.04. The DRAM is 16G DDR3 and the CPU is Intel E5-2603. The data in experiment consists two parts. One is real-world database and the other is randomly synthesized data sets.The real-world database comes from Amazon Simple Storage Service (Amazon S3) [18], it is the top 1 million domain names. Besides,we build a word bank, each synthesized prefix is random choose n words as its n components.We average the number of prefixes with different lengths. For example, there are 9 thousand prefixes, and the number of longest name prefix components is 18. It means the number of prefix is nearly 5 hundred in each length.
5.2 Time consumptions
Firstly, we discuss randomly synthesized data sets.
Figure 5 and figure 6 demonstrate two cases respectively. Since the name prefixes are randomly synthesized, the number of each length-component prefix is average. Binary search is much better than LNPM. This tendency becomes even more remarkable as the longer prefixes and the more number of prefixes. And notice that time consumptions between BSH and BBS become smaller along with the prefix numbers become larger, although BBS is still worse than BSH.
Figure 7 and figure 8 show the same cases with real-word database. In figure 7, since there is only 4-conponent of the longest name prefix and all name prefixes match successfully, binary search has no obvious advantage.All three algorithms have similar hash Table lookup. Considering the several extra bloom filter lookup, BBS is little worse than BSH.However, in the worst case shown in figure 8, binary search usually with less hash Table lookup. The gap between BSH and BBS is also small. Moreover, the gap become even smaller with the larger number of name prefixes.
As the above, BBS and BSH is much better than LNPM in time consumptions. BBS is a little worse than BSH, but the gap between them is smaller along with the larger number of name prefixes.
5.3 Memory consumptions
Now we discuss memory consumptions among the three algorithms.
Table 1 shows in randomly synthesized data sets, the memory consumptions of three algorithms. LNPM is the best in memory consumptions because there is not any additional cost in it. In this case, the memory consumptions in BSH is 1.7 times than LNPM. It indicates that the BSH has a very bad performance in memory consumptions, especially in the situation of large-scale data and long component name prefixes. However, BBS spends only 4% extra memory consumptions than LNPM.Considering the time consumptions, the memory consumptions of BBS is well acceptable.

Fig. 5 All matched prefixes in randomly synthesized data sets

Fig. 6 All unmatched prefixes in randomly synthesized data sets

Fig. 7 All matched prefixes in real-world database

Table I Memory consumptions in different algorithm

Fig. 8 All unmatched prefixes in real-world database
VI. CONCLUSION
NDN needs fast and memory efficient lookup algorithm. Binary search become a good choose because it can provide much less times of hash lookup than LNPM. However, applying it in NDN directly may lead the memory explosion. In this paper, we present a NDN lookup algorithm called BBS. BBS using bloom filter to reduce the memory consumptions while keeping the fast lookup. This paper make some experiments to evaluate the performance of BBS. Through two kinds of data,this paper proves that BBS can be balanced in memory consumptions and time consumptions. The memory consumptions expands only 4%. And BBS may perform even better when name prefixes become longer or the database becomes larger.
ACKNOWLEDGEMENT
The work was supported by the National Natural Science Foundation of China (Grant No.61472130 and 61702174), and the China Postdoctoral Science Foundation funded project.
[1] Named data networking (NDN). http://www.named-data.net
[2] H. Dai, B. Liu, Y. Chen, and Y. Wang. “On pending interest Table in named data networking.”Proc. eighth ACM/IEEE symposium on Architectures for networking and communications systems, 2012, pages 211–222.
[3] V. Jacobson, D. K. Smetters, J. D. Thornton, M.F.Plass, N. H. Briggs, and R. L. Braynard. “Networking named content.” Proc. fifth international conference on Emerging networking experiments and technologies, ACM, 2009, pages 1–12.
[4] JH. Ran, N. Lv, D. Zhang, et al. “On performance of cache policies in named data networking.”Proc. ICACSEI, 2013, pages 668-671.
[5] W. So, A. Narayanan, and D. Oran. “Named data networking on a router: fast and dos-resistant forwarding with hash Tables.” Proc. the ninth ACM/IEEE symposium on Architectures for networking and communications systems, IEEE,2013, pages 215–226.
[6] M. Varvello, D. Perino, and J. Esteban. “Caesar: A content router for high speed forwarding.” Proc.the second edition of the ICN workshop on Information-centric networking, ACM, 2012, pages 73–78.
[7] Y. Wang, H. Dai, T. Zhang, W. Meng, J. Fan, and B. Liu. “Gpu-accelerated name lookup with component encoding.” Computer Networks, vol.57, no.16, 2013, pp. 3165–3177
[8] Y. Wang, K. He, H. Dai, W. Meng, J. Jiang, B. Liu,and Y. Chen. “Scalable name lookup in NDN using eあective name component encoding.” Proc.ICDCS, 2012, pages 688-697.
[9] Y. Wang, Y. Zu, T. Zhang, K. Peng, et al. “Wire speed name lookup: A gpu-based approach.”Proc. NSDI, 2013, pages 199–212.
[10] C. Yi, A. Afanasyev, L. Wang, B. Zhang, and L.Zhang. “Adaptive forwarding in named data networking.” ACM SIGCOMM Computer Communication Review, vol. 42, no. 3, 2012, pp.62–67.
[11] H. Yuan, T. Song, and P. Crowley. “Scalable ndn forwarding: Concepts, issues and principles.”Proc. ICCCN, 2012, pages 1–9.
[12] L. Zhang, D. Estrin, J. Burke, et al. “Named data networking (ndn) project.” Transportation Research Record Journal of the Transportation Research Board, vol. 1892, no. 1, 2014, pp. 227-234.
[13] Z. Zhou, T. Song, and Y. Jia. “A high-performance url lookup engine for url filtering systems.” Proc. ICC, 2010, pages 1–5.
[14] Yuan H, Crowley P. “Reliably Scalable Name Prefix Lookup” Proc. Eleventh ACM/IEEE Symposium on Architectures for NETWORKING and Communications Systems, IEEE Computer Society, 2015,pages 111-121.
[15] Yang, T, Liu, A. X, Shahzad, et al. “A Shifting Bloom Filter Framework for Set Queries.” Proceedings of the Vldb Endowment, vol. 9, no. 5,2016, pp. 408-419.
[16] Tong Yang, Gaogang Xie, Yanbiao Li, et al.“Guarantee IP Lookup Performance with FIB Explosion.” Proc. SIGCOMM, 2014, pages 39-50.
[17] Wang Y, Pan T, Mi Z, et al. “NameFilter: Achieving fast name lookup with low memory cost via applying two-stage Bloom filters.” Proc. INFOCOM, IEEE, 2013, pages 95-99.
[18] https://aws.amason.com/cn/s3
- China Communications的其它文章
- Migration to Software-Defined Networks: the Customers’ View
- Software Defined Traffic Engineering for Improving Quality of Service
- Towards a Dynamic Controller Scheduling-Timing Problem in Software-Defined Networking
- Efficient Virtual Network Embedding Algorithm Based on Restrictive Selection and Optimization Theory Approach
- Energy-Efficient Joint Content Caching and Small Base Station Activation Mechanism Design in Heterogeneous Cellular Networks
- Dual Power Allocation Optimization Based on Stackelberg Game in Heterogeneous Network with Hybrid Energy Supplies

