Dual Power Allocation Optimization Based on Stackelberg Game in Heterogeneous Network with Hybrid Energy Supplies

Shiyu Ji＊, Liangrui Tang Mengxi Zhang Shimo Du2 State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University,Beijing 02206, China.

2 China Mobile Communication Group Ltd, Zhe Jiang Branch, Hangzhou, 310006, China

* The corresponding author, email:15210726562@163.com

I. INTRODUCTION

Today and in the foreseeable future, video traffic constitutes a significant 51 percent of the mobile traffic volume and is expected to increase to 67 percent by 2017 [1,2]. The exponential growth of mobile traffic volume gives rise to the sharp increase of wireless terminals and nodes, which contributes to a rapid increase in the energy consumption and carbon emission of the information and communication technology (ICT) sector. As described in [3,4], the world wide annual CO2emission and energy consumption of ICT industry will be 235M to and 414Twh respectively. Therefore, reducing power consumption of the ICT system is crucial to wireless network.

Nowadays, energy harvesting is proved that it can reduce the power consumption of the wireless networks [5-7].The sources of energy harvesting can be divided into two types:electromagnetic radiation (EM) and renewable energy (RE) [8]. In wireless network, the EM radiation, appearing in the form of radio frequency (RF), can be received by antennas and converted to power. However, the energy density of EM radiation is relatively low [9],while the RE resources can provide a higher energy density. Moreover, the RE is more economical and green than conventional energy which generated from fossil fuels [10]. While the RE resources enable green energy supply,the main shortcoming is that the energy may not guarantee a sufficient power supply for fa-cilities due to its space-time instability.

Thus, multiple studies focus on the optimal energy allocation to guarantee the operation of energy harvesting network. Authors in [11] investigate the optimal transmission policy in a point to point communication system in which the transmitter is equipped with an energy harvesting device. In [12], a traceable model for heterogeneous cellular networks with energy harvesting is established and an online power allocation algorithm is proposed to approach the optimal utility performance in energy harvesting networks [13]. However, as discussed in [14], a base station powered by RE solely would not guarantee the quality of service(QoS).

Therefore, a hybrid energy harvesting wireless system is designed and the power allocation in this system is also investigated [15-23]. The authors in [16] propose a structure of hybrid energy harvesting wireless system and the energy efficient power allocation algorithm is proposed in [17]. The authors formulate the power allocation as an optimization problem and solve it via Lagrange dual decomposition.In [18], the authors focus on minimization of the total on-grid energy consumption and an off line algorithm is proposed, but this work ignore the selfishly of users which want to obtain much more resource. The literature [19]develops effective power allocation optimization and green energy cooperation algorithm to improve the performance of cellular networks powered by hybrid energy sources. However,these methods are an optimization problem solved by the method using single person decision theory [20], these works would not promote the utility level of each users and it is difficult for users to benefit from the decision making. So, a large number of game theory method in power allocation is proposed where different sets of users cooperate to achieve an optimal solution or compete between each other to benefit selfishly. The authors in [21]propose a price-based power allocation in non-orthogonal multiple access systems. In this work, the authors use Stackelberg game theory in a centralized wireless system. However, this work only consider the power obtained from on-grid system and is not suitable for the hybrid energy supplies system. The authors in [22] show an optimal power allocation strategy which aims to minimize the on-grid power consumption with the delivery latency constraint. However, the work ignores that the energy output of renewable energy source is intermittent. The authors in [23] investigate the power allocation in energy harvesting cognitive radio networks (CRNs) and formulate the power allocation between primary user and secondary user as a non-cooperative game. Since, in heterogeneous network with hybrid energy supplies, the achieved satisfy degree would be different due to the different proportion of green energy and on-grid energy.In this paper, we study dual power allocation among networks and users in heterogeneous networks using a game theoretic approach.This problem can be formulated as a seller’s market competition, and is suitable to be solved by Stackelberg game. The Stackelberg game is a hierarchical game which consider the networks and users. In each game stage,the leader, i.e., network as a seller to determine the price of the dual power according to the users’ demand. Then, the users as buyers to purchase the optimal amount of dual power to maximize their utilities. The main objective of this Stackelberg game formulation is to increase the revenue of the networks and maximize the users’ utilities.

The contributions of this paper can be summarized as trifold.

● In this paper, the benefit and the cost of users and networks is investigated, and the utility of each user and network in the hybrid energy source system is designed.

● The communication between users and networks is formulated as a Stackelberg game.The network plays a role as a leader, while users as followers.

● The existence of Nash equilibrium is proved in this paper. Then we derive an iteration algorithm to optimize the dual power allocation to maximize the utilities of users and networks.

In order to maximize the utilities of users and networks, a dual power allocation algorithm based on Stackelberg game to is proposed in this paper.

The rest of the paper is organized as follows. Section II presents the energy harvesting wireless system model. In Section III, the utility functions of the Stackelberg model are formulated, and the existence of NE is proved.Section IV shows the numerical results and we conclude this paper in Section V.

II. ENERGY HARVESTING WIRELESS SYSTEM MODEL

In this section, the system model with hybrid energy source and the harvested energy model in green energy are presented.

2.1 system model

The system under consideration is depicted in figure 1, which consists of a macro wireless network and M small networks. The total bandwidth of the system is B Hertz and there are N sub-channels in each network.K={12,,...,K} is the set of the users which access to the network and is allocated the same sub-channel.

Fig. 1 System model

Fig. 2 Harvested Energy Model

In our model, the base station is equipped with hybrid energy source which can be powered by green energy and on-grid energy. In each time slot, the base station will harvest the energy from green energy source and on-grid energy source. The network users access to would translate the green energy and on-grid energy to the transmission power. We assume that the transmission power of kth user is Pk.It is obviously that the transmission power of kth user cannot superior the maximization transmission power Pkmax.

2.2 harvested energy model of green energy

In this sub-section, the harvested energy model of green energy is considered. For convenience and without loss of generality, the process is assumed to be a discrete time process.

As shown in figure 2, the harvested energy model is include T time slot. At the beginning of the tth time slot, the harvested energy from green energy source can be denoted by EH(t ), obviously EH(t)≥0.

As we assumed, the user would access to the network and gain the transmission power in the beginning of each time slot. The duration of each time slot is L. As we considered, the power allocation method would independence for each time slot although the harvested energy EHis different for each time slot. So, in one time slot, the peak energy should be guaranteed. We assume that the power translated by green energy and ongrid energy is PHkand PCkrespectively for kth user. It is obvious that Pk=PCk+PHk.The PC=(PC1,PC2,...,PCn) and PH=(PH1,PH2,...,PHn) are the transmission power acquired from green energy source and on-grid energy source. Obviously, in each time slot, the harvested energy from green energy source is limited as shown in figure 2, and the maximization transmission power from green energy source for each user can be calculated as:

where, PHkmaxis maximization transmission power from green energy source. So the constraints should be maintained:

III. THE DUAL POWER ALLOCATION STRATEGY BASED ON STACKELBERG GAME

In the hybrid energy wireless system, the users would like to obtain the best service quality and the wireless network wants to hold the benefit via the resource trading. To realize the expectation of the networks and users, we define the users as buyers, networks as sellers,and power grabbed from green energy system and on-grid system as commodities in the Stackelberg game as follows.

The Stackelberg leadership model is a twostage game in which the leader (network)announces the price of power grabbed from green energy system is ΠHand on-grid system is ΠCrespectively. The price strategy of network can be written as (ΠC,ΠH). Then the follower (user) moves sequentially by adjusting the power allocation strategy to maximize its own utility function. At last, the leader and the followers are able to reach to their own utility function’s maximization which means Stackelberg model gets solution called SE. SE consists ofwhereare the power allocation strategies to maximize the user utility function andare the power prices grabbed from green energy system and on-grid system respectively that minimize the network utility function.

3.1 Stackelberg game analysis

1) The utility function of users

The user utility function would represent the satisfaction degree of the user. Each user wants to get the best benefit at the least possible expense. In this context, we consider that the benefit of user obtained from the transmission power translated by green energy would weaker than the on-grid energy in the perspective of the stability. To imitate the transmission rate equation, the benefit function is formulated as:

where,01＜＜β is the penalty factor parameter which indicates the weakness of green energy source. γkCand γkHare the parameters to measure the contribution of different energy source to the benefit of users obtained which can be calculated by:

where gkis the gain of channel which the kth user is allocated to.is the channel gain of the jth user whose channel is the same as the kth user. We assume that the additional baseband noise is a white Gaussian noise with zero mean and variance σ. From the environmental pollution and the economic perspective, the on-grid energy would bring lot of pollution and cost more than green energy. So, the cost function for each user can be calculated as:

In formulation (7), the PCk2is the cost to the environment and economy using on-grid energy source. So, the utility function of the user is:

In wireless system, the signal to Interference plus noise ratio (SINR) of user should meet the requirement to maintain its performance. Assuming that the recognition SINR of receiving set isit is obvious that the practical SINR can be formulate as,according to the formulation (5) and (6). So the constraint is:

2) The utility function of network

In network side, the network sells the commodity (power) to the users and announce the price of the power. The network is supposed to make decisions based on the corresponding behaviors of all users. Thus, the utility function of network can be formulated as:Since, the dual power allocation strategy based Stackelberg game is a two-stage game,and two games are defined as: 1) the dual power game (DPG) at the users’ side and 2)the prices game(ΠG)at the network side.

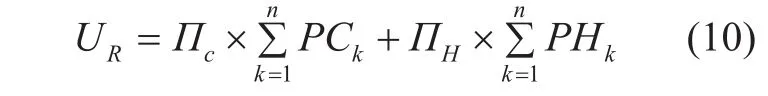
3.2 User side: the DPG

As analyzed above, the Stackelberg game is composed of DPG at users’ side and the ΠG at the network side. Thus, the DPG and ΠG are investigated respectively. In this section,we investigate the DPG. The DPG can be defined aswhich denotes the non-cooperative dual power purchases for the given green energy source power price ΠHand on-grid energy source power price ΠC, respectively. PCkand PHkare dual power supplied by ongrid energy source and the green energy source sets of kth user and {Uk(·)} is the kth user utility function. Thus, the resulting utility for the kth user can be formatted as Uk(PC,PH;(ΠC,ΠH)) An alternative notion Uk(PCk,PHk,PC−k,PH−k;(ΠC,ΠH))can be used to explain that the kth user utility function value is related to its own dual power allocation strategies PCkand PHk, respectively. Moreover, PC−kand PH−kdenote the game outcome of other users.

As we investigate the DPG above, the DPG is a non-cooperative game which Nash equilibrium (NE) is a 2-Dtuple satisfying the following objective function：

where, the PC*=and PH*=denote the dual power allocation strategies reach to NE. At the NE, given the dual power levels share with the other users, no user can improve its utility by making individual changes in its own power supplied by on-grid energy source power and the green energy source [25]. The existence of NE would be investigated as follows:

Theorem 3.1: The strategic non-cooperative game DPG=admits at least one NE if ∀i∈K: the set(PCk,PHk) is a non-empty compact subset of the Euclidean space, and the utility functioncontinuous and quasi-concave.

Anchored in Theorem 3.1, the DPG admits at least one NE. because the strategy space for each user is a bounded closed set and the utility function of each user is continuous. Furthermore, the joint concavity of utility function of kth user can be proved as in [26] with formulation (12)

where, θHand θHare the adjust step parameters of utility function, andandare the dual power allocati

on strategies in the iteration τ+1. The kth user keeps updating using formulation(13)and (14) until reaching to the NE. It is obvious that the DPG reaches to NE whenthat isare equal to zero.

The formulation(13) and (14) is based on the marginal profit function defined in microeconomics. By definition in Reference [25],marginal profit is the term used to refer to total when marginal cost is subtracted from marginal revenue. Using the marginal approach to maximize profits, a firm should continue to produce a good until marginal profit is zero. Therefore, each user would ensure that∂Uk/∂PCk=0 and ∂Uk/∂PCk=0 at any time. Otherwise, if the transmission power allocated to the kth user is less than the optimal one, ∂Uk/∂PCkand ∂Uk/∂PCkwill change from zero to positive and the kth user will increase in the next game stage. Otherwise,if the transmission power allocated to the kth user is more than the optimal one, ∂Uk/∂PCkand ∂Uk/∂PCkwill change from zero to negative, and the kth user will decrease at the next game stage. So, ∂Uk/∂PCkand ∂Uk/∂PCkwould be zero at the end of game and obtain the optimal value.

3.3 Network side: the ΠG

The ΠG is the non-cooperative dual power price game in network side, which can be denoted asthe network selects the optimal dual power prices ΠCand ΠHto maximize the network utility function and the {UR(·)} is the network utility function as defined in (10).In formulation(10), the utility function of network has the following properties. First, when ΠC=0 and ΠH=0, the UR=0. Second, URapproaches the zero when ΠC→∞ and ΠH→∞. Third,the utility function value is finite if the user number is finite. To get the optimal dual power price ΠCand ΠHin maximization of the utility function, we treat the ΠG as a dynamic game and set the dual power price of the update algorithm as:

where, φCand φHare the step length adjustment parameters, t is the iteration number and δ is iteration speed adjustment parameter. The convergence of the ΠG can be the similar as the DPG. In addition, we substitute NE of the dual power PC*and PH*into the formulation (10) and the first derivative of the URcan be calculated as:

Algorithm 1 Dual power allocation algorithm based Stackelberg game

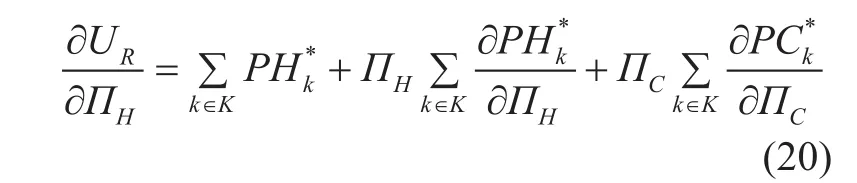
Table I Simulation parameters

Table II The ratio of green energy source power to total power vs β

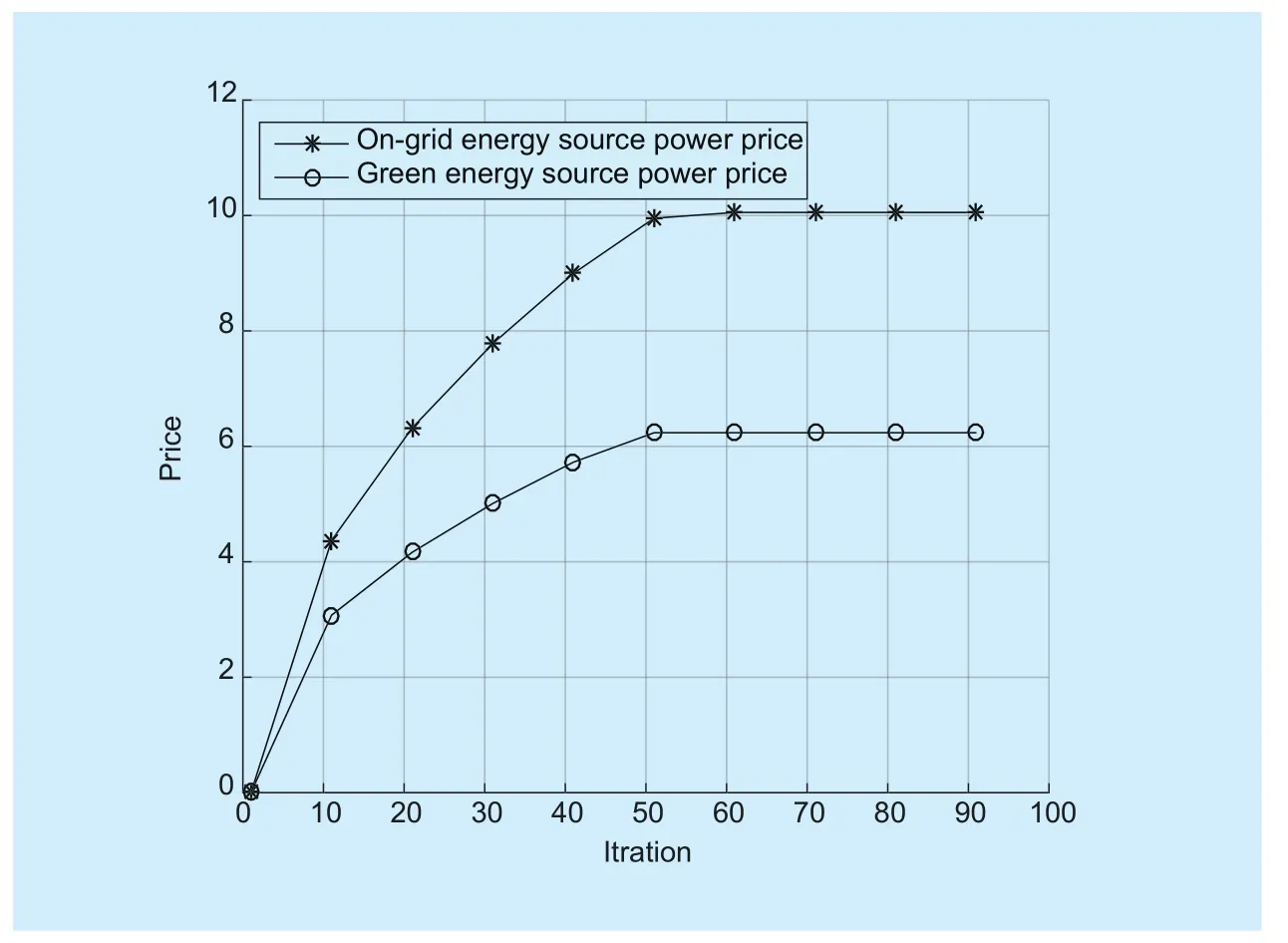
Fig. 3 The dual power price versus iteration

Because the formulations(19) and (20) are difficult to solve, an approximate formulation is proposed to approach the result.where, ξΠCand ξΠHare the small numbers that represent the incremental change in green energy source power price and on-grid energy source power price. It is obvious that the ΠG reaches to equilibrium when, that is to sayand∂UR/∂∏Hare equal to zero. As the proposed algorithm in(15)-(18), when the dual power price is less than optimal one, ∂UR/∂∏Cand∂UR/∂∏Hwill change from zero to positive and the power price will increase in the next game stage. Otherwise, if the dual power price is more than the optimal one,and∂UR/∂∏Hwill change from zero to negative, and price will decrease at the next game stage. So ∂UR/∂∏Cand ∂UR/∂∏Hwould be zero at the end of game and obtain the optimal value.

As analyzed above, the Stackelberg game is a two-stage game, and the solution of DPG and ΠG is investigated above. The dual power allocation algorithm based on Stackelberg game can be described in algorithm 1.

IV. SIMULATION ANALYSIS

As shown in figure 1, our scenario models a two-tier heterogeneous network consist of one Macro network and several small networks.The parameters can be shown in table 1.

The table 2 shows the ratio of green energy source power in total power variation with penalty factor parameter β at the NE. it can be seen the ratio would increase with the increasing of ratio. The green energy source power is almost near the on-grid source power when β.=09 because that the penalty would be weakness and user would tend to select the green energy source power.

Figure 3 shows the dual power price allocation strategies with the iteration increasing when M=2. It is obvious that the dual power price increasing rate would decrease with the increasing of iteration. It also can be seen that the on-grid energy power price is higher than green energy source power because the high price of the on-grid energy source power would reduce the utilization of on-grid energy for users.

Fig. 4 The dual power of users versus iteration (a) the dual power of macro user (b) the dual power of small user 1 (c) the dual power of small user 2

Fig. 5 The users utilities versus iteration (a) the macro user utility versus iteration (b) The small user1 utility versus iteration (c) the small user2 utility versus iteration

Figure 4 is the dual power allocation strat-egies of macro user and small users with the iteration increasing. In figure 4(b) and figure 4(c), the green energy source power would increase before decreasing. The reason is that the on-grid energy source would change even if the green energy source power achieve the optimal value. That is to say, in DPG, the NE of dual power is not the same as that of the green energy source power or the on-grid energy source power. It is also can be seen that the transmission power of small user is less than that of macro user because the macro user would be in the edge area of macro network.

Figure 5 shows the variation of the utility function value with the iteration increase in different value of β. It is obvious that the users would only can be allocated the on-grid energy source power that β=0. In table 1, we can see the allocated on-grid energy source power is almost equal to the green energy source power when β.=09, and it is equal to the half of the green energy source power when β.=05. In figure 5(a), we can see the utility function value of the macro user would increase along with the value of β increasing because the transmission power allocated to the macro user is huge,the cost to the environment would be huge when using on-grid energy source and the cost would be reduced when using the green energy source. However, the small users would not be the same with the macro user. In figure 5(b) and figure 5(c), the utility function value in small user is highest when β=0. The reason is that the transmission power is tiny and the benefit of using on-grid energy source would be higher than the cost.

In figure 6, the amount of green energy in macro network is limited, and the small user green energy source power and on-grid energy source power would increase. As shown in figure 6(b), it is difficult to get the SE due to the limit of harvesting energy in the small and macro network.

In figure 7, the amount of green energy in macro network is not limited, and the green energy source power would be higher than the power in figure 6(a). The reason is that the macro user allocated much green energy source power to reach the SE when the harvesting energy in small network is limit.

V. CONCLUSION

Fig. 6 The transmission power with different amount of green energy in small network when the amount of green energy in macro network is limit

Fig. 7 The transmission power with different amount of green energy in small network when the amount of green energy in macro network is not limit

In this paper, a Stackelberg game to investigate the dual power allocation problem of heterogeneous network with hybrid energy supplies was used. Then the existence of NE for this game is proved. An iteration algorithm is also proposed which can maximize the utilities of users and networks. The simulation result reveals that the SE can be reached using the proposed algorithm，and the users’ utilities maximization would be conflict with the maximization of green energy utilization when the total transmission power is low and it would reach consensus when the transmission power is high.

ACKNOWLEDGMENT

The work is supported by the Beijing Natural Science Foundation (4142049), 863 project No. 2014AA01A701 and the Fundamental Research Funds for Central Universities of China No. 2015XS07.

[1] X Zhang, W Cheng, H Zhang, “Heterogeneous statistical QoS provisioning over 5G mobile wireless networks,” IEEE Network, vol. 28, no. 6,2014, pp. 46-53.

[2] P Pirinen, “A Brief Overview of 5G Research Activities,” Proc. International Conference on 5G for Ubiquitous Connectivity. 2014, pp.17-22.

[3] A Fehske, G Fettweis, J Malmodin, et al, “The global footprint of mobile communications:The ecological and economic perspective,” IEEE Communications Magazine, vol. 49, no. 8, 2011,pp. 55-62.

[4] S Lambert, H.W Van, W Vereecken, et al,“Worldwide electricity consumption of communication networks,” Optics Express, vol. 20, no.26, 2012, pp. 513-24.

[5] K Huang, M Kountouris, V.O Li, “Renewable Powered Cellular Networks: Energy Field Modeling and Network Coverage,” IEEE Transactions on Wireless Communications, vol. 14, no. 8,2014, pp. 4234-4247.

[6] T Han, N Ansari, “On Optimizing Green Energy Utilization for Cellular Networks with Hybrid Energy Supplies,” IEEE Transactions on Wireless Communications, vol. 12, no. 8, 2013, pp. 3872-3882.

[7] A Kwasinski, “Increasing sustainability and resiliency of cellular network infrastructure by harvesting renewable energy,” IEEE Communications Magazine, vol. 53, no. 4, 2015, pp. 110-116.

[8] M.L Ku, W Li, Y Chen, et al, “Advances in Energy Harvesting Communications: Past, Present, and Future Challenges,” IEEE Communications Surveys & Tutorials, vol. 18, no. 2, 2016, pp. 1384-1412.

[9] S Kim, R Vyas, J Bito, et al, “Ambient RF Energy-Harvesting Technologies for Self-Sustainable Standalone Wireless Sensor Platforms,” Proceedings of the IEEE, vol. 102, no. 11, 2014, pp.1649-1666.

[10] T Han, N Ansari, “Powering mobile networks with green energy,” IEEE Wireless Communications, vol. 21, no. 1, 2014, pp. 90-96.

[11] P Blasco, D Gunduz, M Dohler. “A Learning Theoretic Approach to Energy Harvesting Communication System Optimization,” IEEE Transac-tions on Wireless Communications, vol. 12, no.4, 2012, pp. 1872-1882.

[12] D Liu, Y Chen, K.K Chai, et al, “Adaptive user association in HetNets with renewable energy powered base stations,” Proc. International Conference on Telecommunications. 2014, pp.93-97.

[13] L Huang, M.J Neely, “Utility Optimal Scheduling in Energy Harvesting Networks,” IEEE/ACM Transactions on Networking, vol. 21, no. 4, 2010,pp. 1117-1130.

[14] Y Mao, J Zhang, K.B Letaief, “A Lyapunov Optimization Approach for Green Cellular Networks With Hybrid Energy Supplies,” IEEE Journal on Selected Areas in Communications, vol. 33,no.12, 2015, pp. 2463-2477.

[15] J Yang, S Ulukus, “Optimal Packet Scheduling in an Energy Harvesting Communication System,”IEEE Transactions on Communications, vol. 60,no. 1, 2010, pp. 220-230.

[16] D Zordan, M Miozzo, P Dini, et al. “When telecommunications networks meet energy grids:cellular networks with energy harvesting and trading capabilities,” IEEE Communications Magazine, vol. 53, no. 6, 2015, pp. 117-123.

[17] D.W.K Ng, E.S Lo, R Schober, “Energy-Efficient Resource Allocation in OFDMA Systems with Hybrid Energy Harvesting Base Station,” IEEE Transactions on Wireless Communications, vol.12, no. 7, 2013, pp. 3412-3427.

[18] J Gong, S Zhou, Z Niu, “Optimal Power Allocation for Energy Harvesting and Power Grid Coexisting Wireless Communication Systems,” IEEE Transactions on Communications, vol. 61, no. 7,2013, pp. 3040-3049.

[19] L Wang, X Zhang, K Yang, “Power Allocation Optimization and Green Energy Cooperation Strategy for Cellular Networks with Hybrid Energy Supplies,” KSII Transactions on Internet and information systems, vol. 10, no, 9, 2016, pp.4145-4164.

[20] T Schwertfeger, “The Single-Person Decision Problem[Game Theory: An Introduction.” Princeton University Press, 2012.

[21] C Li, Q Zhang, Q Li, et al, “Price-Based Power Allocation for Non-Orthogonal Multiple Access Systems,” IEEE Wireless Communications Letters,vol. 5, no. 6, 2016, pp. 664-667.

[22] P.D Diamantoulakis, K.N Pappi, G.K Karagiannidis, et al, “Autonomous Energy Harvesting Base Stations With Minimum Storage Requirements,” IEEE Wireless Communication Letters,vol. 4, no, 3, 2015, pp. 265-268.

[23] L. Chen, L. Huang, H. Sun, H. Xu, et al, “Achieving primary secrecy in energy harvesting CRNs using stackelberg game,” Proc. WCSP, 2015, pp.1-5.

[24] Z Wang, B. Hu, Chen S, et al, “Interference Pricing in 5G Ultra-Dense Small Cell Networks: A Stackelberg Game Approach,” IET Communications, vol. 10, no. 15, 2016, pp. 1865-1872.

[25] M. Osborne , A. Rubinstein, “A Course in Game Theory,” MA: MIT Press, 1994

[26] B Wang, Z Han, K.J.R Liu, “Distributed Relay Selection and Power Control for Multiuser Cooperative Communication Networks Using Stackelberg Game,” IEEE Transactions on Mobile Computing, vol. 8, no. 7, 2009, pp. 975-990.

[27] Y Jiang, S.Z Chen, H.U Bo, “Stackelberg gamesbased distributed algorithm of pricing and resource allocation in heterogeneous wireless networks,” Journal on Communications, vol. 34,no. 1, 2013, pp. 61-68.