Efficient Virtual Network Embedding Algorithm Based on Restrictive Selection and Optimization Theory Approach

Haotong Cao, Zhicheng Qu, Yishi Xue,4, Longxiang Yang,3,4,＊

1 College of Communication and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing, China

2 Wolfson School of Mechanical, Electrical and Manufacturing Engineering, Loughborough University, Leicestershire, UK

3 Key Laboratory of Broadband Wireless Communication and Sensor Network Technique, Ministry of Education, Nanjing University of Posts and Telecommunications, Nanjing, China

4 Wireless Communication Key Laboratory of Jiangsu Province, Nanjing University of Posts and Telecommunications, Nanjing, China

* The corresponding author, email: yanglx@njupt.edu.cn

I. INTRODUCTION

DUE TO the ossification of current network and conflicting policies between different network stakeholders, network virtualization(NV) [1]-[5] has been recognized as one key technologies for the future network. Network virtualization [1] is an enabling technology to remove the resistance of the current network,particularly for the IP network [3].

However, several challenges still exist and prevent network virtualization from being implemented in the real networking environment [4]. One main challenge is how to embed virtual networks (VNs), with resource demands of virtual nodes and links, on the shared substrate network (SN) that has finite resources efficiently. The challenge is known as so called virtual network embedding(VNE). Since the VNE problem requires a simultaneous optimal resource allocation of virtual nodes and links, it is considered as a multiway separator problem and NP-hard [8].Many VNE algorithms, such as references[9]-[24], have been proposed to deal with the VNE problem. However, to simplify the NP hardness, these algorithms either assume that the SN supports the path splitting [25], or conduct the node and link embedding in two separate stages. Thus providing a feasible or sub-optimal embedding of each VN in the end.According to optimization techniques adopted,multiple VNE algorithms can be classified into two main categories [6]. One category is the heuristic algorithm, the other category is the exact algorithm [7]. With respect to the heuristic algorithms [9]-[14], a feasible embedding of each VN aims to be found in polynomial time. In many cases, the embedding per VN is not optimal, even not sub-optimal. To the exact algorithms [15][16][19]-[22], the optimal or sub-optimal embedding per VN can be calculated in small-scaled network scenario, after a lot of computation. However, it is impossible to calculate out the optimal mapping in moderately sized network. A large number of binary variables contribute to not finding the optimal embedding in reasonable time. In many cases,it even cannot converge to a sub-optimal embedding.

To achieve a trade-off between the heuristic and exact algorithms, this paper proposes an efficient algorithm VNE-RSOT, on the basis of the restrictive selection and optimization theory approach [26], to map virtual nodes and links per VN on the shared substrate network simultaneously. The restrictive selection aims to select candidate substrate nodes and candidate substrate paths. The restrictive selection contributes to largely cutting down on the number of binary variables, adopted in the following optimization theory approach.The algorithm VNE-RSOT is made up of two different sub-algorithms. One sub-algorithm aims to achieve a minimization of substrate resources, the other is to minimize the substrate resource consumption and achieve the substrate load balancing simultaneously.Node-link constraints considered in this paper are virtual node location, virtual node capacity and virtual link bandwidth while common VNE algorithms only take node capacity and link bandwidth into account. To highlight the efficiency of VNE-RSOT, a simulation against several typical and state-of-art heuristic and a pure exact algorithms is also made. Numerical results reveal that the algorithm VNE-RSOT outperforms the best selected heuristic in many aspects. For instance, VNR acceptance ratio of VNE-RSOT is, at least, 10% higher than the best-behaved heuristic (see figure 2).

The rest of this paper is organized as follows. Section II summarizes the related work.While in Section III, it describes the universal virtual network embedding problem. Section IV elaborates on the algorithm VNE-RSOT.Section V conducts a simulation against several typical and state-of-art heuristic algorithms and a pure exact algorithm. Section VI concludes this paper in the end.

II. RELATED WORK

VNE is a well-studied problem, requiring a simultaneous node and link mapping optimization, and can be formulated as an unsplittable flow problem [25]. Many VNE algorithms have been proposed in the literature. This section only discusses VNE algorithms that are closely related to this paper. Readers who have great interest in other issues of VNE, such as VN survivability [23][28][29], can refer to references [6][7] for a detailed survey of VNE.

2.1 Typical VNE heuristic and exact algorithms

Zhu et al. [9] proposes a one-stage heuristic algorithm. The goal of this heuristic algorithm is to achieve low load on substrate nodes and links, with the assumption of infinite substrate resources and no constraints on the location requirements of virtual nodes per VN. Though hardly restricting the VNE solution space and impractical in real networking, [9] is a good start of VNE research at that period. Only link mapping is conducted in reference [9].

While in reference [10], another typical heuristic algorithm, proposed by Yu et al.,applies the greedy method to implement the virtual node mapping in the first step. Dijkstra’s algorithm [27] and multi-commodity flow method [25] are then used to deal with the link mapping. In [10], virtual nodes and links of the same VN are embedded separately. Reference [10] also introduces the concept of path splitting to accept more proposed VNRs and relieve substrate link loading. However, this algorithm will lead to a level of resource fragmentation that is unfeasible for accepting VNs with large sizes. In addition, only constraints of node capacity and link bandwidth are considered. Therefore, there is no restriction of the VNE solution space. If the size of SN is large,the computational complexity will increase.

A backtracking method based on sub-graph isomorphism is proposed in [11]. Reference[11] manages to online map virtual nodes and links per VN, taking constraints of node capacity and link bandwidth into consideration.Due to the approach of sub-graph isomorphism, virtual nodes and links of the same VN are embedded simultaneously in [11]. Some other node-link constraints, such as node location, are not included. Reference [11] is a sub-optimal algorithm and the computation of processing VNRs will largely grow with the number of VNRs increasing. In additional, the scale of substrate network is limited in [11].The execution time grows exponentially with the substrate network scale expanding.

Cheng et al. [12] proposes a topology-aware node mapping approach that uses the Markov Random Walk model to measure the node capacity and joint link bandwidth. The virtual links, whether splittable or unsplittable,are then mapped onto substrate network either using the k-shortest path, or multi-commodity flow approach. In reference [10], virtual nodes and links of the same VN are therefore embedded separately. In addition, reference [12]still leads to the problem of resource fragmentation, same to the reference [10].

The algorithm of reference [14], based on the conference version [13], is widely recognized as a representative heuristic algorithm in VNE research area. Chowdhuryet al. firstly solves the VNE problem by adopting the mixed integer programming (MIP) model of the optimization theory [27]. Due to the exponential complexity of pure MIP model, Chowdhuryet al. has to modify the MIP model into a linear programming (LP) model and relaxes the integer constraints on continuous values.Chowdhuryet al. uses the LP model to solve the virtual node mapping. If the solution of LP model is feasible, the virtual links are assigned to corresponding substrate paths by using the Dijkstra’s algorithm [27] or the multi-commodity flow [25] approach. Therefore, the algorithm proposed in reference [14] is not able to embed virtual nodes and links of the same VN simultaneously. Though the formulation coordinates node and link mapping, it is not an effective algorithm in the long term.

Houdi et al. [15] proposes an exact algorithm to map one VN across multiple SNs,fighting for the minimization of VN provision cost. The authors use the max-flow and mincut method to split one VN into several parts in the first step. The number of parts is equal to the number of substrate networks. Then the ILP model is adopted to map each part of the VN to each SN. Therefore, virtual nodes and links of the same VN are embedded simultaneously. Node capacity and link bandwidth are taken into account. In addition, multiple SNs can been viewed as a large substrate network in [15]. The topology and resource information of substrate networks are known in ad-vance. However, in practical networking environment, InPs of different substrate networks are not willing to show topology and resource information of their private networks.

Reference [16], another variation of reference [14], adds the constraint of allowing more than one virtual node per VN to map onto the same substrate node and uses the pure MIP model [14] to deal with VNE problem directly. Thus embedding virtual nodes and links of the same VN simultaneously. The goals of[16] are to minimize the consumption of link bandwidth and the number of active substrate nodes. This paper is also the first attempt in VNE energy aware problem. Only node capacity and link bandwidth are taken into account in the simulation work. Due to the computational complexity of MIP, the scales of SN and VNRs are limited small (a substrate network of 15 nodes and a virtual network of 5 nodes). On the basis of reference [16], Su Sen et al. [17][18] further develops the VNE energy aware problem and proposes a specific network model for solving VNE energy aware problem.

While in reference [19], presented by Melo et al., a pure ILP model, embedding node and links simultaneously, is adopted to solve the offline VNE problem. The goal of reference[19] is to minimize the VN cost. Two new constraints, node location requirement and virtual link delay, are introduced. However, both two constraints are not formulated in the ILP model. In general, the algorithm of reference[19] is an exact algorithm and fights for the minimization of substrate resource consumption. Constraints of node capacity and link bandwidth are considered in embedding the proposed VNs.

Mijumbi et al. [20], similar to references[21] and [22], is another variation of [14] to solve the VNE problem. Virtual nodes and links of the same VN are not embedded simultaneously in [20]. Constraints considered are same to what are considered in [14]. In the first step, [20] formulates the VNE problem by adopting the pure MIP model [14]. Relaxing the constraints of variables to take on continuous values. The MIP model is relaxed into LP model. With solving the LP model and getting the node mapping done, the shortest path is selected again [29]. The authors then derive the corresponding dual MIP model. The dual model is used to ensure the selected paths legitimate. The VN assignment which costs less substrate resources is preferred. The time complexity decreases a lot, comparing with solving the pure MIP model directly. This exact algorithm also improves the performance of VNR acceptance ratio in the long term, comparing with the heuristics [12][14]. However,no theoretical analysis of the time complexity is presented in reference [20].

2.2 Summary

To sum up, most existing VNE heuristic algorithms make assumptions for simplification,such as infinite substrate resources [9] and ignoring virtual node or link constraint[9], while other heuristic algorithms solve the VNE problem in two separate stages [12][18], using the greedy method [10] or LP approach [14]in node mapping stage and optimizing the link mapping by using Dijkstra’s algorithm or the multi-commodity flow approach. What’ more,embedding virtual nodes and links of the same VN separately is not able to achieve the optimal VN embedding, even in restricted solution space.

To exact algorithms[15][16][19], related to this paper, they can be classified into two categories. One category is to use the pure MIP/ILP model of the optimization theory to solve the VNE problem directly[15][16]. This category of algorithms can embed virtual nodes and links of the same VN simultaneously.However, a large number of binary variables of the MIP/ILP model will lead to the exponential time complexity. This category of algorithms can only be applied in small-scaled network scenario. Therefore, these algorithms are impractical in real networking environment. The other category [20][21][22] is to relax the MIP/ILP model into the LP model at first. Then solve the LP and get an initial VN embedding. Employ column/path generation,allowing for the use of a number of meaningful paths, and add more paths as needed until a sub-optimal embedding is obtained, within the restricted solution space. This category of algorithms also can be viewed as a mixture of exact and heuristic algorithms. The exact approach comes in the first stage. Then comes the heuristic method. This category of algorithms usually embed virtual nodes and links of the same VN separately [20][21][22].

Different from the previous VNE algorithms in the literature, the VNE-RSOT is a combination of heuristic and exact algorithms(the heuristic method is adopted in the first place). VNE-RSOT can find the optimal VN embedding within restricted solution space,within limited time. The VNE-RSOT has several highlights, comparing with previous VNE algorithms. First of all, the VNE-RSOT, on the basis of restrictive selection and optimization theory, is an efficient VNE algorithm. The restrictive selection contributes to selecting candidate substrate nodes and candidate substrate paths. Therefore, the number of integer variables, used in the following optimization theory approach, will be largely cut down,comparing with the pure MIP/ILP model. The following optimization theory approach in this paper can be solved in reasonable time.The optimal VN assignment will be found in the restricted solution space. Then, the VNERSOT combines node and link mapping in one stage. After selecting candidate substrate nodes and paths, the VNE-RSOT adopts the ILP model to embed virtual nodes and links per VN at the same time. Optimal mapping of the VN is able to be found in the restricted solution space. The node mapping is an important part in VNE since it determines the efficiency of the link mapping. Coordinating both two stages will lead to better resource utilization [14][16]. Combining both two stages into one stage will further enhance the resource efficiency. Finally, the authors of this paper also make a comprehensive simulation against the representative and latest heuristic algorithms and a pure exact algorithm to further highlight the efficiency of VNE-RSOT.Numerical results prove that VNE-RSOT is an efficient VNE algorithm and can embed virtual nodes and links simultaneously effectively.

III. VNE NETWORK MODEL AND VNE PROBLEM DESCRIPTION

This section talks about the VNE problem.The substrate network and virtual network are modeled at first. Main index notations throughout this paper are listed in table 1.Measurements of network resources are presented in this section. The embedding process of VN is also stated. At last, evaluation metrics are introduced and defined.

3.1 Network description

1) Substrate network: The substrate network is modeled as a weighted undirected graph GS=(NS, LS), where NSis the set of all substrate nodes of the SN and LSis the set of all substrate links. Each substrate node m∈NSis characterized by its node capacity,,and the node location, loc(m). The location of substrate node m, loc(m), is defined by x and y coordinates in this paper (according to the simulation platform in Section V). With respect to substrate links, each substrate link mn has a finite bandwidth. Due to the nature of undirected graph of SN, the value ofis equal to. The set of all substrate paths in the SN is denoted by notation. Correspondingis the set of all paths between end nodes m and n without any loop.is one path selected from the mn path set. The right part of figure 1 is a substrate network.The numbers over the links are available link bandwidth and numbers in circles are available node capacity. For simplicity, the location of each substrate node is omitted in this figure.

2) Virtual network request: A virtual network request is described as a weighted undirected graph GV=(NV, LV), where NVis the set of all virtual nodes of the VNR and LVis the set of all virtual links. Each virtual node M is characterized by the required node capacity, CVM, and desired virtual node location,Loc(M). The allowed maximum deviation of virtual node M is LR(M). Expression 1 briefly shows the deviation relationship between virtual node M and any selected substrate node m in this paper. The deviation must be within the radius LR(M) of virtual node M. With respect to each virtual link, each virtual link MN has a required bandwidthThe left part of figure 1 presents two virtual network requests.The numbers over the links are required link bandwidth and the numbers in rectangles are node capacity demands of virtual nodes. The location requirement of any virtual node is set to be a pair of real numbers by x and y coordinates, along with its required deviation LR(M).

Fig. 1 One Substrate Network and Two Virtual Network Requests

Table I VNE Notations

3) VNE Notations: The main notations used in this paper for embedding VNs are listed in table 1 below.

3.2 Measurements of network resources

In VNE research area, to quantify the resource usage of substrate nodes, the available node capacity of a substrate node RS(m) is defined as follows:

where M ↑ m denotes that the virtual node M is mapped onto the substrate node m.

Similarly, the available bandwidth of each substrate link is determined by the bandwidth before the VN mapping and the consumed bandwidth after the VNE assignment. Expression 3 below shows the definition.

where MN ↑ mn denotes that virtual link MN passes through the substrate link mn after conducting the embedding of the VN.

In VNE, every virtual link per VN may occupy one or more substrate paths after two end nodes are mapped. Though no link aggregation (splittable flow) in this paper, one substrate path may accommodate one or more substrate links. Based on this fact, the available bandwidth of the substrate path mn is given by follows:

where one selected single substrate path mn is made up of one or more substrate links, the substrate link ab included.

3.3 Embedding process of VN

Every time a VNR arrives, the SN will firstly determine whether to accept the VNR or not,according to the remaining substrate resources. If the VNR is accepted, the SN will refer to one specific VNE algorithm for embedding the VNR and spares enough resources of the substrate nodes and paths to fulfill all resource demands of the VNR. When the VNR expires,the allocated resources are leased to SN.

Generally, the embedding of a VNR consists of two main components: the component that fulfills the mapping of virtual nodes, and the component that ensures the mapping of virtual links.

1) Virtual Node Embedding: Each virtual node of the same VNR must be assigned to a different substrate node of SN. This does benefit to the flexibility, manageability and stability of SN. The assignments of all virtual nodes are determined by a node-mapping function FN( ) : NV→ NS.

FN(M) ∈NS

FN(M) = FN(N), if and only if M=N

subject to

where expression 5 is to ensure the node capacity requirement of any virtual node M must not exceed the remaining capacity of the substrate node that accommodates M; expression 6 shows the node location constraint. the expression aims to ensure that the deviation relationship between any virtual node M and its selected substrate node must be within the radius LR(M). The node location constraint is very crucial in VNE study. For instance, a hot event is happening in Xin Jie Kou (Nanjing,China). A virtual node acts as the broadcasting node. The virtual node and some virtual nodes form a star topology. According to the broadcasting requirements, proposed by the Service Provider (SP) [6], the broadcasting virtual node must be embedded to a substrate node, within the maximum allowed derivation/distance, e.g. 2 km of the virtual node. That is to say, upon embedding the broadcasting virtual node, only substrate nodes, within the maximum allowed distance, are taken into consideration. To the service aspect, substrate nodes, near to the event site, enable to decrease service propagation delay and further ensure quality of service (QoS), comparing with other substrate nodes, far away from the event site; to the algorithm aspect, the number of variables can be cut down on. The node location constraint contributes to decreasing the computation complexity, comparing with the algorithm, no considering the node location constraint.

In the node embedding stage, both two expressions must be fulfilled at the same time.

2) Virtual Link Embedding: Each virtual link of the same VNR is mapped onto a single substrate path (unsplittable flow) in this paper between the corresponding substrate nodes that host the end virtual nodes. Different paths do not interfere with each other. This is a key characteristic of VNE-RSOT. The link embedding is implemented according to the link-mapping function FL( ) : LV→ PSfor all virtual links per VN.

where expression 7 is to ensure the link bandwidth demand of any virtual link MN must not exceed the available bandwidth of one selected substrate path that accommodates MN.The lower part of figure 1 shows also shows the embedding results of two virtual networks,along with node-link resource requirements fulfilled.

3.4 Mapping metrics

In order to assess the performance of any selected VNE algorithm, and compare with other algorithms, evaluation metrics are necessary to be defined. This subsection introduces some basic and important metrics in VNE area.

1) The revenue of a VNR: Similar to the definition in [13] and [14], the revenue of a VNR is defined:

As derived from the expression 8, the universal revenue of a VNR is set to be the sum of all virtual node capacity and virtual link bandwidth of this VNR [6]. Wight factors (α and β) are used to balance different types of network resources.

2) The cost of a VNR: Though expression 8 gives an insight into how much revenue can be earned by accepting a VNR, it is useless without knowing how much substrate resources are consumed for embedding the VNR. In order to evaluate the effect of embedding the VNR,expression 9 formulates the cost of embedding a VNR:

As shown in expression 9, the left part of expression 9 is same to what is defined in expression 8. In VNE, any substrate path may consist of multiple substrate links. Therefore,therepresents the number of substrate links in the path mn, mapped onto MN. Based on this, the cost of substrate links is the sum of the product of the number of substrate links and consumed virtual link bandwidth.

3) VNR acceptance ratio: The VNR acceptance ratio, in expression 10 below, is used to evaluate an algorithm’s ability of batch processing VNRs and is a rather important metric in VNE research. It is determined by the number of accepted VNRs a’ and the number of proposed VNRs a in a time window:

4) Average Link Path: The average link path, shown in expression 11 below, is used to measure an algorithm’s ability of consuming substrate resources and is a quite important metric in VNE research. It is determined by the number of occupied substrate links b’ and the number of virtual links b in the accepted VNs. Smaller average link path, more available resources will be left for accepting the coming VNs:

With respect to some other VNE metrics,average node utilization and execution time,readers can refer to references [6] and [7] for a detailed definition.

IV. EFFICIENT VNE ALGORITHM VNERSOT

This section elaborates on the algorithm VNERSOT for solving the VNE problem. The restrictive selection is presented at first. Then,two kinds of variables, used in the optimization theory approach, are defined. Next, two different objective functions, making up the algorithm VNE-RSOT, are presented. Each object is considered as a sub-algorithm of VNE-RSOT. At last, the constraints are formulated and presented. Node-link constraints are also included. The index notations used in this section are same to what have been used in Section III.

4.1 Restrictive selection

The restrictive selection of each VN aims to select candidate substrate nodes and substrate paths ahead, for the following optimization theory approach. Virtual node location requirement (for all virtual nodes of the same VN) and restrictive number k (for all virtual links of the same VN) must be fulfilled in the restrictive selection.

Every time a VN comes, the location constraint of all virtual nodes is taken into consideration at first. The required location of any virtual node M is defined by x and y coordinates, (XM, YM). The virtual node M maps onto one substrate node m, (Xm, Ym),within the allowed location distance LR(M).Equation 12 and 13, the detailed version of expression 6, aim to ensure that the Euclidean Distance between M and m must not exceed the allowed location radius LR(M) of virtual node M. All substrate nodes that are within the allowed location radius LR(M) of virtual node M make up the substrate node set of virtual node M. To sum up, the number of substrate node sets is equal to the number of virtual nodes of the VN. To deal with the occasional situation where two different virtual nodes(M and N) have the same candidate substrate node, m, within their own allowed location radius (LR(M) and LR(N)), the smaller allowed location radius of the virtual node (M or N)selects m as the candidate substrate node.

After selecting the candidate substrate nodes of each virtual node of the VN, the restrictive number k is adopted to select the candidate substrate paths. The restrictive number k is valid to all virtual links of the VN in the restrictive selection stage.

For instance, if the restrictive number k of a VN is set to be 3. For any two different virtual nodes, having a logical link between them, M and N, the number of substrate links in the path( m is one candidate substrate node of the virtual node M, n is one candidate substrate node of the virtual node N) must not exceed 3. These paths, each consisting of no more than 3 substrate links, are selected and make up the candidate substrate path set of the virtual node pair, M and N. The pseudo code of restrictive selection stage is described in Restrictive Selection. Particularly, in line 2 of Restrictive Selection, the VNi, having the lowest revenue among the proposed VNs, is preferred to be embedded. It is owing to the fact that the goal of this paper is to evaluate different VNE algorithms’ abilities of batching processing VNs in a time window. The average VNR acceptance ratio, the ratio of accepted VNs, is an important metric in VNE research.To accept as many VNs as possible, the VNs are processed in increasing order in this paper.Therefore, the VNiof lowest revenue are in priority.

With completing the restrictive selection per VN, candidate substrate nodes and candidate substrate paths are gathered. The optimization theory approach is then adopted to model the restricted problem and implement the further embedding. An efficient and optimal embedding of each proposed VN is able to be found in the restricted/sharped solution space. It is due to the fact the procedures of selecting candidate nodes and paths contribute to largely decreasing the number of binary variables, adopted in optimization theoryapproach. Therefore, the embedding can be found in reasonable time. Numerical results in Section V will prove the efficiency of VNERSOT. The optimization theory approach of VNE-RSOT is formulated in the following subsections in detail. The ILP model of optimization theory is adopted.

Restrictive Selection

4.2 Variables

The binary variable x is used for the assignment of virtual node M to its candidate substrate node m. x is defined in expression 14.With respect to the virtual links per VN, the binary variable y is defined in expression 15.Different from the link-link based MIP model of reference [14] and the link-link based ILP model of reference [19], the model in this paper is a link-path based ILP model.

4.3 Objective functions

Constructing proper and appropriate objective functions is one challenge in the VNE research. It is important to optimize the allocation of substrate resources so as to improve the efficiency of substrate resources. This subsection presents two objective functions, with regard to different paradigms. Each objective function is a sub-algorithm of the VNE-RSOT.

1) Cost Function (CF): In general, the dominating aspect in VNE study is to minimize the cost of accepted VNRs in order that more substrate resources can be reserved and available.Leaving more substrate resources will lead to accommodating more coming VNRs. The CF is selected as the first sub-algorithm of VNERSOT. The CF, aiming at consuming less substrate node capacity and link bandwidth,is formulated in expression 16. All binary variables of the ILP model are included. The right part of expression 16 is the link mapping cost of the VN, which is to be processed. Two binary virtual link variables,and, aim to ensure that substrate path mn maps onto the virtual link MN or NM, with two end nodes(m and n) mapped successfully. For instance,when substrate path mn is mapped onto the virtual link MN,is equal to 1. Meanwhile,virtual nodes m and n map onto substrate nodes M and N. Therefore, the corresponding variableis equal to 0. α and β are weight factors in this expression. Similar to references [14] and [19], α and β are set to be equal in this paper.

2) Cost and Load Balancing Function(CLBF): Expression 16 goes well in situations where the SN has abundant network resources.When the degree of flexibility in the resource assignment process is of great importance, it is necessary to consider VN cost and substrate load balancing at the same time. Both two goals can be constructed and achieved in this part. Expression 17 below is the objective function CLBF. The CLBF is another important sub-algorithm of VNE-RSOT. Same to references [14] and [19], α and β are set to be equal. All binary variables of the restricted ILP model are also included in CLBF.

4.4 Constraints

To ensure the correct embedding of nodes and links, and obey to the conservation law of nodes and links, proper constraints are formulated and presented below.

1) Virtual Nodes’ Mapping to Substrate Nodes: Equation 18 below aims to assure that once any virtual node of the same VNR is mapped, only a substrate node of the SN is assigned to that virtual node.

2) Substrate Nodes’ Mapping to Virtual Nodes: Equation 19 is to ensure that each substrate node of the SN can accommodate no more than one virtual node per VNR. Both equation 18 and 19 vividly describe the relationship between virtual node M and substrate node m in VNE.

3) Conservation of Node Capacity: Equation 20 aims to ensure that each selected substrate node m must have reserved available node capacity for accommodating the demand of virtual node M.

4) Assignment of Virtual Links to Substrate Paths: Different from the previous algorithms[14][19], the unsplittable flow constraint [25]is used here. Each virtual link per VNR is allocated to one selected candidate substrate path with fulfilling the requirements of two end nodes. Due to the goal of achieving the minimization of substrate cost, it is necessary to adopt to the unsplittable flow constraint.Equation 21 shows the unsplittable flow con-straint of virtual links.

5) Link Bandwidth Conservation: Equation 22 aims to ensure that the selected substrate path mn must spare enough link bandwidth to accommodate the bandwidth demand of virtual link MN that maps onto the selected path mn.

V. PERFORMANCE EVALUATION

This section presents the simulation settings followed by the results. This section primarily elaborates on quantifying the efficiency of VNE-RSOT. Several typical and state-of-art heuristic algorithms and a pure exact algorithm (link-path based ILP model) are selected to make up the simulation part.

5.1 Simulation environment and settings

To evaluate the VNE-RSOT, a discrete event simulator in JAVA has been implemented. The open source software tool GLPK [30] is used to solve the linear programming problem of VNE-RSOT, with two different objects, and the exact algorithm VNE-ILP. Since network virtualization is still an emerging field, the actual characteristics of the substrate network and virtual networks are still not well understood. Therefore, synthetic network topologies are used to evaluate the proposed VNE algorithms.

The simulation work is implemented and evaluated on the ‘Simulation Platform for Scotfield Cao’ [34], originating from the opensource project ALEVIN [31]. The authors of this paper further program and develop the simulation project. The VNE-RSOT is also coded by the authors. Some codes are available in [34], for free.

In this paper, the substrate network is generated using the Waxman topology method[32], which has been integrated as a function module in ‘Simulation Platform for Scotfield Cao’. Different from the universal exact solution simulation settings (15 nodes, ref [16])and heuristic solution simulation settings (50 nodes, ref [13][14][24]), the authors of this paper aim to achieve a balance of the simulation settings, particularly for the scale of substrate network. Therefore, the number of substrate nodes is set to be 40 in this paper. Set α=0.4 and β=0.3 in the Waxman model of substrate network. The substrate network of this paper can be viewed as a medium-scaled substrate network. The node capacity and link bandwidth of substrate nodes and substrate links are integers uniformly distributed between 50 and 100. Each substrate node is randomly located within a uniformly distributed position between 0 and 100 on x and y coordinates.

VNRs are also generated using the Waxman topology method. It is set that VNRs arrive in a Poisson process and evaluated by varying VNRs arrival rate from 2 VNs per time window to 9 VNs per time window. The arrival rate increases by 1 each time. Each VNR has an exponentially distributed lifetime with an average value of μ=1000 time units.These parameters are similar to what are set in reference [14] and [19]. To every VNR,the number of virtual nodes is an integer and follows a uniform distribution between 2 and 8. Link connectivity parameters of each VNR are same to what are set in substrate links. The node capacity and bandwidth requirements of virtual nodes and virtual links are integers uniformly distributed between 1 and 20. Virtual nodes are randomly located within a uniformly distributed position between 0 and 100 on x and y coordinates. The distance deviation of each virtual node is an integer and uniformly distributed between 3 and 8.

To avoid an insight into two opposite case scenarios, such as with a very high or low VNR acceptance ratio, many trials are necessary to be conducted for each arrival rate. In this paper, 10 trials are made for each arrival rate. In each trial, a new set of VNs and a new substrate network are generated. All simula-tions are set to run up to 50000 time units to remove the initial transient phase effect [33]and to present the steady-state performance.

All simulations for different VNE algorithms are run on a Window 8 Desktop, with an Intel® Core (TM) CPU i7-4790＠ 3.6GHz Processor and 16.00G RAM Machine. The time per network embedding is registered. The GLPK version 4.58 is used to solve the linear programming problem of VNE-RSOT and pure exact algorithm VNE-ILP. The restrictive number k ranges from 1 to 3 in this paper.With k increasing to ∞, the VNE-RSOT will be turned into the pure link-path based ILP exact algorithm (considering all substrate paths and largely increasing the number of binary variables) VNE-ILP. In VNE-RSOT, weight factors (α and β) are all set 1 in this paper. To the VNRs proposed in a time window, the VN with smaller revenue is preferred. Evaluation metrics are derived from Section III-D and reference [6].

5.2 Compared VNE algorithms

Eight VNE algorithms make up the simulation part. Besides of two sub-algorithms of VNERSOT, remaining algorithms are Greedy Node Mapping with Shortest Path Link Mapping(G-SP) [10], Randomized or Deterministic Coordinated Node Mapping with Shortest Path Link Mapping (ViNE-SP) [14], Virtual Network Embedding with Degree, Farness and Betweeness (VNE-DFB) [35], Virtual Network Embedding with Degree and Cluster-ing Coefficient Information (VNE-DCC) [36],the Pure Link-Path based ILP exact algorithm(VNE-ILP). These algorithms are typical or latest in VNE research and are all slightly modified to fit into the simulation of this paper(e.g. node location considered). All VNE algorithms are enumerated in table 2, along with short characteristic descriptions.

Table II Compared VNE Algorithms

5.3 Efficiency and eあectiveness of VNE-RSOT

1) VNR Acceptance Ratio: figure 2 depicts the average VNR acceptance ratio as a function of VNRs arrival rate. VNR acceptance ratio is an important metric in evaluating different VNE algorithms. As can be observed from figure 2,the acceptance ratio of all selected algorithms almost decays linearly with the variation on the VNRs. This decay shows the fact that there are no infinite substrate resources for embedding increasing proposed VNRs. In addition,the VNE-RSOT, with two different objects,outperforms the selected heuristics. The difference between the best heuristic and VNERSOT-CF is at least 10%. It is run as expected because the ILP model of VNE-RSOT is applied to solve the VNE problem after the restrictive selection. Therefore, optimal mapping of each VN, with respect to one object, can be obtained in the restricted solution space. When to the heuristics, a feasible mapping is tried to be found. Another reason for the results is the nature of the VNE-RSOT. The VNERSOT considers the universe of all possible embedding solution in the restricted solution space, rather than some potential solutions.For example, the first case with 2 VNRs in a time window, the VNE-RSOT will accept all VNRs, while the acceptance ratios of the remaining heuristics are between 65% and 80%.The VNE-RSOT-CLBF achieves the highest acceptance ratio while the lowest ratio is obtained by G-SP. On the whole, the VNE-RSOT outperforms the heuristics in all scenarios.VNE-RSOT is an efficient and effective VNE algorithm through the simulation. If a feasible assignment of a network scenario exists, the VNE-RSOT will find out the optimal mapping in the restricted solution space. However, it is not always the case for the heuristic algorithm.Frequently a feasible assignment will be found out though it may be the sub-optimal mapping in some cases.

In addition, in a stable VN arrival rate (e.g.2 VNs in a time window), with the restrictive number k (from 1 to 3) increasing, the VNR acceptance ratio of VNE-RSOT (CF/CLBF)will slightly increases, too. When k increases to ∞, the VNE-RSOT will turn into the pure exact algorithm VNE-ILP. All possible embedding assignments of each VN are considered by VNE-ILP. The optimal embedding per VN is selected. The VNR acceptance ratio of VNE-ILP will increase, comparing with the VNE-REOT. Therefore, the VNE-ILP algorithm is considered as the normalized version of the VNE-REOT. As can be concluded from the figure 2, the VNE-ILP can calculate out the embedding results when the VN arrival rate is no more than 5. However, with the number of VNRs increasing to 6, it is difficult to calculate out the optimal embedding of each VN in limited time. Many factors, such as exponentially increasing binary variables and ILP model solvers (GLPK in this paper),contribute to this phenomenan. Therefore, the embedding results (VNR acceptance ratio,node utilization and execution time) of VNEILP are not plotted in these situations (the number of VNRs in a time window is more than 6). This is in accord with the previous VNE studies [14][20][21]. Therefore, the pure ILP/MIP exact algorithm cannot be applied in the medium-sized VNE network scenarios.

2) Node Utilization: The average node utilization as a function of VNRs arrival rate is depicted in figure 3. With the arrival rate increasing, the node utilization of all selected algorithms increases, too. When the number of VNRs is small, i.e., 2 VNRs, the node utilization does not go beyond 25% and 35% for the heuristics and VNE-RSOT respectively.As illustrated in figure 3, the VNE-RSOT consumes more resources of substrate nodes than the heuristics, which is expected according to the performance of VNR acceptance ratio.The reason for VNE-RSOT having a larger node utilization than the heuristics lies in VNE-RSOT’s ability of accommodating more VNRs than the heuristics. When the number of VNRs is large, the algorithm, VNE-RSOT, is able to embed VNRs efficiently and loads the substrate nodes to full capacity. To the pure VNE-ILP, it considers all possible mappings and further loads all the substrate nodes to full capacity. Every time the embedding is calculated out, the optimal embedding is presented.Comparing with the selected algorithms, the node utilization of VNE-ILP is therefore the highest. With VNRs increasing to 6, the embedding can not be calculated out optically in the simulation work. This situation owes to the fact that the number of binary variables grow exponentially, as analyzed in above subsection.

3) Link Utilization: The link utilization is plotted in figure 4 and does not have the same behavior according to the VNRs arrival rate for all algorithms, as shown in figure 3 for the node utilization. It is evident that the algorithm VNE-RSOT, especially for VNE-RSOTCLBF, has lower utilization on the substrate links; in the extreme scenario (9 VNRs per time window) the average link utilization of VNE-RSOT-CLBF is around 65%. With respect to the highest link utilization, ViNE-SP has a link utilization of around 70%.

Fig. 2 VNR acceptance ratio

Fig. 3 Average node utilization

Fig. 4 Average link utilization

The differences in the link utilization result from the link mapping strategy. For instance,if the object is to consume less bandwidth, the shortest path method (SP) will be adopted and the corresponding average link utilization will be high. Since the node and link mappings are two separate stages in VNE. The performance of node mapping will have a great influence on the following link mapping stage. In figure 4,these algorithms (i.e. G-SP), which use greedy node mapping, have a lower link utilization though SP approach is adapted in the link mapping. Based on this, it is of great importance to simultaneously map virtual nodes and links according to the mathematical programming model. Therefore, the VNE-RSOT behaves well in link utilization generally. To the universal version of VNE-RSOT (VNE-ILP),the average link utilization behaves well and is around 55% (5 VNRs in a time window).

4) Average Link Path: figure 5 shows the average link path as a function of VNRs arrival rate. Comparatively speaking, it runs as expected. With the number of VNRs increasing,the average link path of all selected algorithms increases, same to the node/link utilization illustrated before. To all selected algorithms,they all prefer to have the paths, consisting of more and more substrate links, mapped onto virtual links in order that more proposed virtual network requests can be accommodated.

In addition, two main discoveries can be also derived from the figure 5. The first discovery is that the VNE algorithms, such as G-MCF, that support path splitting and adopt to the multi-commodity fl ow method will lead to a larger average link path than others, i.e.G-SP, that do not support path splitting. The second discovery is that the VNE-RSOT has a better link path than all the heuristics. This discovery lies to the restrictive selection and ILP model of VNE-RSOT. With running the VNERSOT, at most one intermediate node (k=2) is allowed in the link mapping stage. Therefore,the average link path of VNE-RSOT is within the range of 1 and 2. One indirect proof of supporting the second discovery is that the advantage of VNR acceptance ratio of VNERSOT model is not apparent than that shown in reference [19], no taking the restrictive selection into consideration. The VNE-RSOT sacrifices part VNR acceptance ratio for improving the performance of average link path.The detailed analysis of quantifying average link path is not illustrated because of limited space.

5) Execution Time: Another important metric for evaluating VNE algorithms is the time that is required to embed the proposed VNRs in a time window. This metric is known as so called execution time. In this paper, the execution time as a function of the VNRs arrival rate is depicted in figure 6.

To make the execution time valuable and worthy illustrated, several items must be set same in advance: i. all algorithms must run on the same computer; ii. all algorithms must run by using the same platform (e.g. ‘Simulation Platform for Scotfi eld Cao’ in this paper); iii.the time to embed proposed VNRs must depend on the physical characteristics (e.g. CPU)of the computer and the nature of the VNE algorithm; iv. the same LP solver (GLPK in this paper) and same LP solving method (i.e.branch and bound method) must be adopted to solve VNE-RSOT, ViNE-SP and VNE-ILP.

Through illustrating the figure 6, three main behaviors can be observed. One behavior is that the execution time of all algorithms increases with the number of VNRs increasing.This is apparent and expected as a function of increased VNRs. More computation, more execution time. The other behavior is that algorithms which perform linear programming operations, VNE-RSOT, ViNE-SP and VNEILP, have more execution time than the pure heuristics in general, such as G-SP, VNEDFB and VNE-DCC. At last, to the VNERSOT, candidate substrate nodes and paths are selected with fulfilling the restrictive selection. Therefore, the number of binary variables decreases a lot. The ILP model of the optimization theory approach is able to be solved in reasonable time, with regard to each object. Constraints of node capacity and link bandwidth are considered simultaneously.However, with the number of k increasing, the number of candidate substrate paths increase exponentially. Thus largely increasing the number of binary variables considered in the ILP model. The execution time will further increase in the end. With the k increasing to∞, the VNE-RSOT will turned into the pure VNE-ILP in the end. The execution time of VNE-ILP grows exponentially with the number of VNs increasing. When the number of VNRs increasing to 6 or more, the embedding cannot be executed. The authors of this paper only plot the execution time of VNE-ILP when the number of VNRs is no more than 5. It is as shown in figure 6 below. This phenomena also indirectly proves the conclusion of references [20][21] that pure VNE exact solution/algorithms are time-consuming and cannot be apply to the medium-sized VNE problem.

Fig. 5 Average link path

Fig. 6 Execution Time of Selected Algorithms

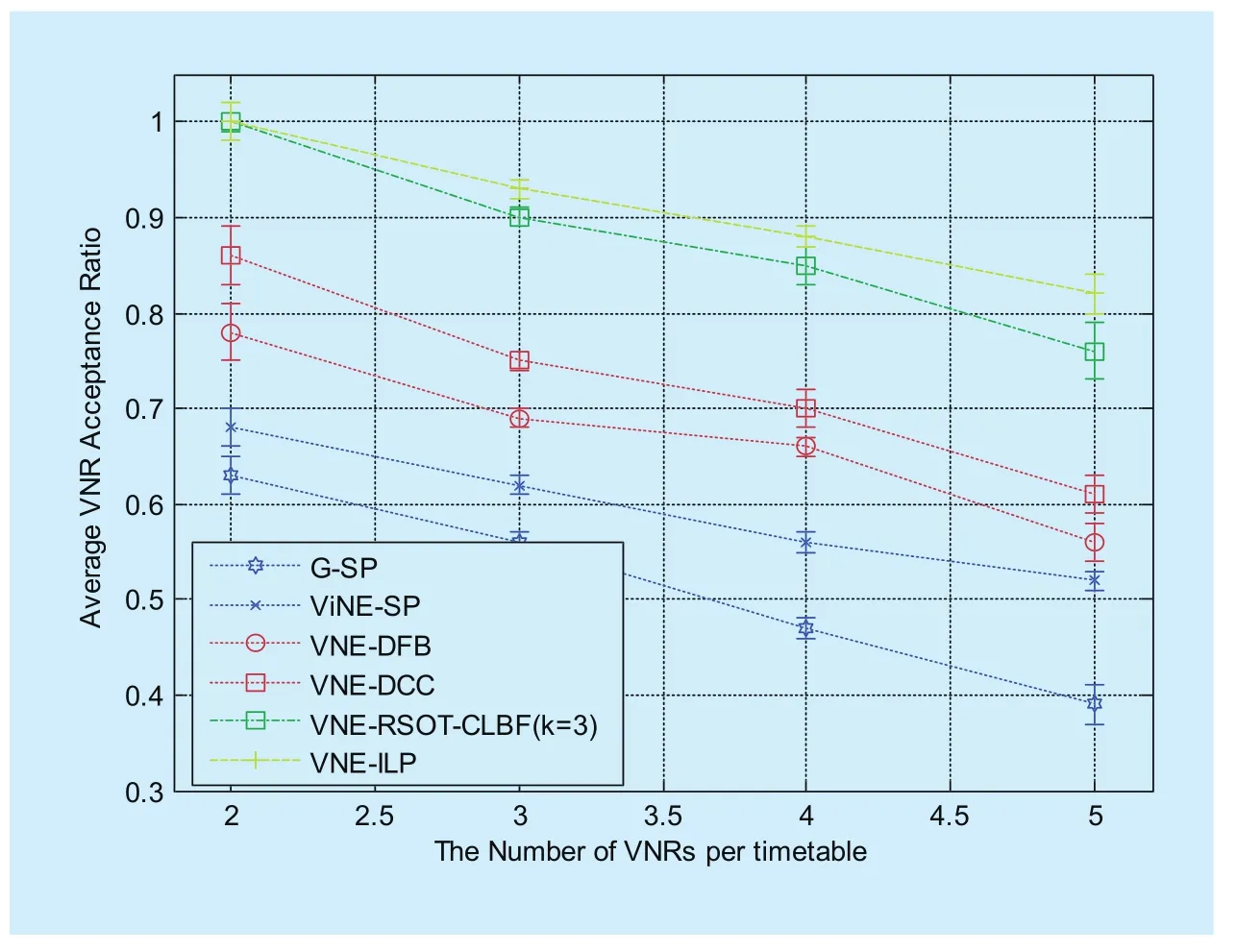
Fig. 7 VNR Acceptance Ratio in Small-scaled Network Scenarios

Fig. 8 Execution Time in Small-scaled Network Scenarios

5.4 Performance comparison in small-scaled and large-scaled network scenarios

As presented above, VNE-RSOT outperforms the typical and latest algorithms in moderately sized network scenarios, such as performances of average VNR acceptance ratio. To further prove this issue true, a simulation, making up of a small-scaled SN with several VNRs and a large-scaled SN with several VNRs,is conducted in this subsection. The VNERSOT-CLBF (k=3), behaving best among the other sub-algorithms of VNE-RSOT above, is selected in this subsection. Five algorithms,G-SP, ViNE-SP, VNE-DFB, VNE-DCC and VNE-ILP, are also selected to make up the simulation. The small-scaled SN is set to be 20 nodes. The large-scaled SN is set to be 100 nodes. Other parameters are same to what are set in Section V-A. Evaluation results are plotted ranging from figure 7 to figure 9 as a function of VNRs arrival rate. Due to the limited space, only two primary metrics, VNR acceptance ratio and execution time are plotted.What’s more, the execution time of 100-node network scenario is not plotted because of the exponential computation of VNE-ILP. To the VNE-ILP, one and a half hours is required for a single embedding involving a SN of 100 nodes and a VN of 5 nodes. Thus omitting the execution time of large-scaled network scenarios.

1) In Small-scaled Network Scenarios: figure 7 is the VNR acceptance ratio as a function of VNRs arrival rate. It is evident that VNERSOT-CLBF (k=3) has a close average VNR acceptance ratio to what is obtained by VNEILP. Other heuristic algorithms have a percentage of, at least 10%, lower than VNE-ILP and VNE-RSOT-CLBF (k=3). That is to say, VNEPO-CLBF is able to behave as well as the VNE-ILP, in small-scaled network scenarios.However, in many cases, researchers are more likely to select VNE-ILP to map proposed VNs. This is due to the fact that the VNE-ILP considers all possible VN assignments and can pick out the optimal VN mapping in the end.

With respect to the performance of execution time, figure 8 illustrates that G-SP,ViNE-SP, VNE-DFB and VNE-DCC have comparatively low execution time than that of VNE-RSOT-CLBF (k=3), in small-scaled network scenarios. G-SP, VNE-DFB and VNEDCC are not mathematical algorithms and are therefore of low time complexity. While to the ViNE-SP, it lies to solving the relaxed LP model. Though solved in polynomial time,they have higher execution time than the G-SP. To the VNE-RSOT-CLBF (k=3), candidate substrate nodes and paths are selected with fulfilling candidate substrate nodes and preliminary paths ahead. The number of binary variables decreases a lot. The ILP model is restricted to be solved in reasonable time.However, the execution time of ILP model is still higher than the relaxed LP model through numerous simulations. To the pure VNE-ILP,the execution time grows exponentially in figure 8. However, the pure ILP model can be applied to solve VNE problem in small-scaled network scenarios, when the time is allowed.

In general, in small-scaled network scenarios, VNE-ILP outperforms the VNR-RSOT.The VNE-ILP enables to achieve the optimal VN assignment, with considering all feasible VN mappings.

2) In Large-scaled Network Scenarios:figure 9 is the VNR acceptance ratio as a function of VNRs arrival rate, in large-scaled network scenarios. Derived from the figure 9, it is evident that the VNE-RSOT-CLBF (k=3) still performs better than the G-SP and ViNE-SP.However, the VNE-RSOT-CLBF (k=3) is unable to act as well as the VNE-DFB and VNEDCC, considering many topology attributes in the node mapping stage. That is to say, in large-scaled network scenario, it is necessary to consider topology information and rank nodes ahead. Essential topology information does benefits to the VN embedding. Simply selecting candidates nodes and using mathematical approaches may lead to poor VNR acceptance ratio in VNE.

Therefore, in the large-scaled network scenarios, the VNE-RSOT is not able to perform as well as these VNE algorithms, considering the topology information and ranking nodes ahead.

According to the illustration in 1) and 2), it can be further concluded that the VNE-RSOT outperforms the typical and up-to-date algorithms in moderately sized networks.

Fig. 9 VNR Acceptance Ratio in Large-scaled Network Scenarios

5.5 Discussion of the allowed maximum distance between each virtual node and potential substrate nodes

To discuss the impact on the overall performance of the different VNE algorithms due to the constraint of the allowed distance between virtual nodes and substrate nodes represented in expressions (12) and (13), a new set of simulation experiments are performed in this subsection. The VNE arrival rate is fi xed to 4 VNRs per trial; the allowed maximum distance between each virtual node and its potential substrate nodes is set to vary between 5 and 20 within intervals of 2.5 distance units.For each considered value of allowed maximum distance, the same settings of VNRs are used. The other remaining parameters, such as virtual nodes per VN and link probability,are all maintained. To further increase the readability of all result figures, only the G-SP,ViNE-SP, VNE-DCC, and VNE-RSOT-CLBF(k=3) are selected in this subsection.

Fig. 10 VNR Acceptance Ratio as a Function of Allowed Maximum Distance

Fig. 11 Node Utilization as a Function of Allowed Maximum Distance

1) VNR Acceptance Ratio: figure 10 depicts the VN request acceptance ratio as a function of the allowed maximum distance between each virtual node and its potential substrate nodes. Two main different behaviors can be observed. Firstly, the average VNR acceptance ratio increases with the allowed distances increasing. This is the case of the VNE-RSOTCLBF (k=3). This behavior is expected as all mapping assignments are considered, where VNRs are initially not mapped due to the distance constraint. With further increasing the permitted distance between virtual nodes and their substrate nodes, more proposed VNs are to be embedded successfully. Secondly,increasing the distance between virtual nodes decreases the acceptance ratio: this is the case of the assignment methods G-SP, ViNE-SP,VNE-DCC.

2) Node Utilization: figure 11 depicts the average substrate node utilization as a function of the allowed maximum distance between virtual nodes and substrate nodes. The behavior observed for each selected VNE algorithm can be compared to that of the VN acceptance ratio.

3) Link Utilization: The average physical link utilization is also depicted in figure 12. Two main behaviors can be observed according to the performances of selected VNE algorithms. One behavior is that G-SP and VNE-DCC both reduce slightly the link utilization with the allowed distance increasing. The ViNE-SP is able to maintain the link utilization, despite some fluctuations may be observed. The other behavior is that the VNERSOT-CLBF (k=3) enables to slightly increase the link utilization, along with the allowed maximum distances increasing. This behavior runs as expected and is in accordance with the increase on the VNR acceptance ratio.

5.6 Discussion of the VNE-RSOT and the NFV problem

In the above subsections, the VNE-RSOT has proven to be an efficient VNE problem and enables to conduct the VN embedding effectively. Generally speaking, the VNE problem can be viewed as the resource allocation in NV. Therefore, the VNE-RSOT is concerned with solving the resource allocation problem optimally, with regard to several objects, such as the embedding cost, QoS, economical revenue and energy efficiency.

To the resource allocation problem in Network Function Virtualization (NFV), it is in the same problem domain with the VNE problem. The outcome of both two problems is the efficient allocation of virtual requests on top of the substrate network infrastructure. There-fore, the strategy and optimization theory approach of VNE-RSOT can also be used in the resource allocation problem of NFV. However,both two problems still have three main differences.

1) In VNE, static virtual network requests are proposed. Topologies of these VNs are fixed. Therefore, virtual nodes are arranged in a predetermined order. In contrast, in the resource allocation of NFV, the input is a network service request composed of a set of Virtual Network Functions (VNFs) with precedence constraints and resource demands that can be denoted by several Virtual Network Function Forwarding Graphs (VNF-FGs). The goal of the first stage of the resource allocation of NFV is to efficiently build a suitable VNF-FG with regard to the Internet operator’s goals.

2) Resource requests may vary depending on the traffic load. For instance, computing resource demands/node capacity of a transcoding VNF vary depending on how many multimedia data have to be transcoded. In addition,link bandwidth requirements change depending on the ordering of VNF instances, whereas resource requests/VNRs are mostly static in VNE.

3) VNE is similar to the second stage of NFV-RA: Virtual Network Function Forwarding Graph Embedding (VNF-FGE). In fact, VNF-FGE is widely accepted as another generalization of VNE. It lies to the fact that,while the VNE only considers one type of physical (networking) device, a wide number of different network functions will coexist in VNF-FGE, mapped in different kinds of hardware devices, such as the networking, computation and storage devices.

For a comprehensive knowledge of the NFV, readers and researchers can refer to reference [37].

VI. CONCLUSION AND FUTURE WORK

Fig. 12 Link Utilization as a Function of Allowed Maximum Distance

This paper presents an efficient and effective VNE algorithm VNE-RSOT to solve the VNE problem. Restrictive selection and optimization theory approach make up the algorithm VNE-RSOT. VNE-RSOT is able to simultaneously embed virtual nodes and virtual links per VN. Two different objective functions are proposed: the CF which aims to minimize the cost of the substrate network; the CLBF which aims to minimize the cost of the substrate network and tries to achieve the load balancing of the substrate network. Each object is regarded as an isolated sub-algorithm. Both two different sub-algorithms make up the VNE-RSOT.

Simulation results vividly reveal how far the selected heuristic algorithms are from VNE-RSOT. In terms of VNR acceptance ratio, the difference between the heuristics and VNE-RSOT is, at least, 10% (see figure 2).The node utilization of VNE-RSOT is also higher than the heuristics because of the fact that VNE-RSOT accommodates more VNs than the heuristic solutions. However, the link utilization of VNE-RSOT is similar to the heuristics. When it is to the performance of average link path, VNE-RSOT outperforms the best-behaved heuristic (see figure 5). All mapping assignments are considered in the restricted solution space. The optimal mapping is able to be found by the algorithm VNE-RSOT. Overall, the VNE-RSOT, consisting of two sub-algorithms, proves to be an efficient VNE approach. Not only the VNE-RSOT provides feasible mapping per VN, but also the performance of VNE-RSOT is better than the heuristics.

Comparing with the pure link-path based exact algorithm VNE-ILP, VNE-RSOT cannot behave as well as VNE-ILP, in terms of the ability of processing each VN. It is owning to the fact that VNE-RSOT only aims to find the optimal embedding of a VN in restricted solution space. VNE-ILP considers each potential embedding in the solution space. VNE-ILP selects the optimal assignment as the output,with respect to the concrete object. However,VNE-RSOT can calculate out the sub-optimal embedding in limited time. The number of binary variables, particularly for the link-path variables, have been largely cut down in the restrictive selection stage. With the number of k increasing to ∞, the VNE-RSOT will turned into the pure VNE-ILP in the end.

For the future work, it is to further study the convergence characteristic of VNE-RSOT.Same to references [20] and [21] (a combination of exact and heuristic algorithms), the accurate time complexity is still necessary to be calculated out, though numerical results have proven the efficiency of VNE-RSOT.Another research direction of VNE is to study the convergence accuracy and convergence time of different optimization algorithms (e.g.branch and bound), used to solve the MIP/ILP model of VNE exact algorithms. Optimization solvers, such as GLPK, CPLEX, act as the black box to directly solve the MIP/ILP model of VNE problem all the time. VNE papers, so far in the literature, have never split this black box to study the concrete convergence characteristic of each optimization algorithm used in solvers deeply. This is also another important VNE research area.

ACKNOWLEDGMENT

Some results have been presented in the 2017 16th International Conference on Optical Communications and Networks(ICOCN'2017).This paper was supported by the National Basic Research Program of China (973 Program)under Grant 2013CB329104, the National Natural Science Foundation of China under Grant 61372124 and 61427801, the Key Projects of Natural Science Foundation of Jiangsu University under Grant 11KJA510001.

[1] T. Anderson, L. Peterson, S. Shenker, and J. Turner, “Overcoming the internet impasse through virtualization,” Computer, vol. 38, no. 4, pp. 34-41, 2005.

[2] N. Chowhury and R. Boutaba, “Network virtualization: state of the art and research challenges,” IEEE Commun. Mag., vol. 47, no. 7, pp. 20-26, July 2009.

[3] N. Chowhury and R. Boutaba, “A survey of network virtualization,” Comput. Net., vol. 64, no. 5,pp. 862-876, 2010.

[4] J. Turner and D. Taylor, “Diversifying the internet,” in Proc. IEEE GLOBECOM, 2005, vol. 2, pp.755-760

[5] N. Feamster, L. Gao, and J. Rexford, “How to lease the internet in your spare time,” Comput.Commun. Rev., vol. 37, no. 1, pp. 61-64, 2007.

[6] A. Fischer, J. Botero, M. Till Beck, H. De Meer,and X. Hesselbach, “Virtual network embedding: A survey,” IEEE Commun. Surveys Tuts., vol.15, no. 4, pp. 1888-1906, 4thQuart. 2013.

[7] H. Cao, L. Yang et al., “Exact Solutions of VNE: A Survey” China Commun., vol. 13, no. 6, pp. 48-62, June 2016.

[8] D. Andersen, “Theoretical approaches to node assignment,” 2002 [Online].Available:http://www.cs.cmu.edu/～dga/papers/andersenassign.ps.

[9] Y. Zhu and M. Ammar, “Algorithms for assigning substrate network resources to virtual network components,” in Pro. 2006 IEEE INFOCOM, pp.1-12.

[10] M. Yu, Y. Yi, et al., “Rethinking virtual network embedding: substrate support for path splitting and migration,” SIGCOMM Comput. Commun.Rev., vol. 38, no. 2, pp. 17-29, Mar. 2008.

[11] J. Lischka and H. Karl, “A virtual network embedding algorithm based on subgraph isomorphism detection,” in Proc. 1stACM Workshop VISA, 2009, pp. 81-88.

[12] X. Cheng et al., “Virtual network embedding through topology-aware node ranking,” SIGCOMM Comput. Commun. Rev., vol. 41, no. 2,pp. 38-47, Apr. 2011.

[13] M. Chowhury, M. Rahman, and R. Boutaba, “Virtual network embedding with coordinated node and link mapping,” in Proc. IEEE INFOCOM, Apr.2009, pp. 783-791.

[14] M. Chowhury, M. Rahman, and R. Boutaba,“Vineyard: Virtual network embedding algorithms with coordinated node and link mapping,” IEEE/ACM Trans. Netw., vol. 20, no. 1, pp.206-219, Feb. 2012.

[15] I. Houidi, W. Louati, and D. Zeghlache, “A distributed virtual network mapping algorithm,” in Proc. 2008 IEEE ICC, pp. 5634-5640.

[16] J. Botero et al., “Energy efficient virtual network embedding,” IEEE Commun. Lett., vol. 16, no. 5,pp. 756-759, May 2012.

[17] S. Su, et al., “Energy-Aware Virtual Network Embedding,” IEEE/ACM Trans. Netw., vol. 22, no. 5,pp. 1607-1620, Oct. 2014.

[18] S. Su, et al., “Energy-aware virtual network embedding through consolidation,” in Proc. IEEE INFOCOM WS-CCSES: Green Networking and Smart Grids, 2012, pp. 2708-2713.

[19] M. Melo et al., “Optimal Virtual Network Embedding: Node-Link Formulation,” IEEE Trans.Netw. and Serv. Manag., vol. 10, no. 4, pp. 356-368, Dec. 2013.

[20] R. Mijumbi et al., “A Path Generation Approach to Embedding of Virtual Networks,” IEEE Trans.Netw. and Serv. Manag., vol. 12, no. 3, pp. 334-348, Sep. 2015.

[21] A. Jarray and A. Karmouch, “Decomposition approaches for virtual network embedding with one-shot node and link mapping,” IEEE/ACM Trans. Netw., vol. 23, no. 3, pp. 1012-1025,Jun.2015.

[22] T. Trinh, H. Esaki, and C. Aswakul, “Quality of service using careful overbooking for optimal virtual network resource allocation,” in Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology(ECTI-CON), 2011 8thInternational Conference on,May 2011, pp. 296-299.

[23] M. Rahman and R. Boutaba, “SVNE: Survivable Virtual Network Embedding Algorithms for Network Virtualization,” IEEE Trans. Netw. and Serv. Manag., vol. 10, no. 2, pp. 105-118, Jun.2013.

[24] Long Gong, Huihui Jiang, Yixiang Wang and Zuqing Zhu, “Novel Location-Constrained Virtual Network Embedding(LC-VNE) Algorithms Towards Integrated Node and Link Mapping,”IEEE/ACM Trans. Netw., vol. 24, no. 6, pp. 3648-3661, 2016.

[25] S. Kollopoulos and C. Stein, “Improved approximation algorithms for unsplittable flow problems,” in Proc. IEEE FOCS, 1997, pp. 426-435.

[26] A. Schrijiver, Theory of Linear and Integer Programming. New York, NY, USA: Wiley, 1998.

[27] T. H. Cormen, C. Stein, R. L. Rivest, and C. E.Leiserson, Introduction to Algorithms, 2nded.New York, NY, USA:McGraw-Hill, 2001.

[28] M. Khan, N. Shahriar, R. Ahmed, and R. Boutaba,“Multi-path link embedding for survivability in virtual networks,” IEEE Trans. Netw. and Serv.Manag., vol. 13, no. 2, pp. 253-266, 2016.

[29] S. Chowdhuryet al., “Dedicated Protection for Survivable Virtual Network Embedding,” IEEE Trans. Netw. and Serv. Manag., vol. 13, no. 4, pp.913-926, May. 2016.

[30] “GLPK(GNU Linear Programming Kit),” Jul. 2016.Available: http://www.gnu.org/software/glpk/.

[31] A, Fischer, J. F. Botero, M. Duelli, et al., “ALEVIN-a framework to develop, compare, and analyze virtual network embedding algorithms,” Electronic Commun. of the EASST, vol. 37, pp. 1-12,2011.

[32] B. M. Waxman, “Routing of multipoint connections,” IEEE J. Sel. Areas Commun., vol 6, no. 9,pp. 1617-1622, 1988.

[33] R. Jain, The Art of Computer Systems Performance Analysis. John Wiley & Sons, 1991, vol.182. Available: http://www.cmg.org/proceddings/1991/91INT145.pdf.

[34] http://pan.baidu.com/s/1gekPZrl.

[35] M. Feng, J. Liao, J. Wang, et al., “Topology-aware virtual network embedding based multiple characteristics,” in Proc. 2014 IEEE ICC, pp.2956-2962.

[36] P. Zhang, H. Yao and Y. Liu, et al., “Virtual network embedding based on the degree and clustering coefficient information,” IEEE Access,vol. 4, pp. 8572-8580, 2016.

[37] J. Herrera and J. Botero, “Resource allocation in NFV: A comprehensive survey,” IEEE Trans.Netw. and Serv. Manag., vol. 13, no. 3, pp. 518-532, Sept. 2016.