函数与方程的思想在高中数学中的应用
陈少婉


函数与方程的思想是高中数学的基本思想之一,是通过建立函数或方程,运用函数的图像、性质等去分析问题,解决问题;更重要的是产生函数或方程的方法,能上升到思想高度主动思考问题.运用函数与方程的相互转化解决零点问题、构建函数解决不等关系问题与最值问题、利用方程的思想解决消参求值问题以及切点弦问题等等,是近年高考的热点和重难点.下面举例说明函数与方程的思想在高中数学解题中的应用.
一、零点问题中的函数与方程思想
函数的零点问题是近几年高考题的高频考点和重难点.许多函数问题要用方程的知识与方法来支持;许多方程的问题,需要用函数的知识与方法去解决.函数思想是对函数内容在更高层次上的抽象、概括与提炼,方程问题的函数视角就是利用函数的图像、性质来研究方程的根及范围问题.
1.1.与函数的零点或方程的根或函数图像的交点个数问题
例题1.1.(1)已知函数y=f(x)的周期为2,当x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图像与函数y=|lgx|的图像的交点共有( )
A. 10个 B. 9个 C. 8个 D. 1个
综上所述,原方程有4个实根.
点评:函数零点问题的解题思路主要有两个方向,一是算出来,即利用方程求根,运用方程的思想求解,二是画出来,即转化为函数图像与轴的交点问题或者两个函数图像的交点问题,运用函数的思想以及数形结合的思想求解.在解题过程中,函数与方程相互转化.本题根据分段函数不同区间的特征,综合运用解方程、构造函数,讨论单调性等方法求解.
1.2求参数的值或取值范围问题
例题1.2. 已知函数f(x)=|x2-1|,g(x)=x2+ax+2,x∈R,若函数h(x)=f(x)+g(x)+2在(0,2)上有两个零点x1,x2求实数a的取值范围.
点评:运用函数的思想转化零点问题,构造的函数不同,解法也不同,但用到的思想方法是相同的,在解题中要注意函数与方程的相互转化.
1.3.借助零点,考查导数探究函数的性质
例题1.3. 设函数f(x)=e2x-alnx.
(Ⅰ)讨论f(x)的导函数f′(x)的零点的个数;
值范围,体现了函数的思想.解题时要注意自变量c的取值范围,即函数定义域的确定.
三、立体几何中的函数方程思想
函数方程思想不仅在代数解题中发挥着重要的作用,而且在立体几何中也有着巧妙的应用.在立体几何的动点问题、最值问题和逆向问题中,通常要运用函数与方程的思想求解.
3.1利用函数的图像及性质解决立几中动点的轨迹问题
例题3.1. 如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上. 过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N. 设BP=x,MN=y,则函数y=f(x)的图像大致是( )
点评:本题是一道立体几何与函数图像相结合的题目,主要考查了函数图像的变化.由于题目中给出了自变量和因变量,如能求出函数解析式,问题即可获解.因此,可根据几何体的特征和条件分析两个变量的变化情况,通过M,N,P作底面的垂线作出M,N在平面ABCD内的正投影,保持其长度不变,从而把空间问题平面化,建立一次函數模型.
3.2利用方程的思想解立体几何逆向题
例题3.2. 如图,已知四棱台ABCDA1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P,Q分别在棱DD1,BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二面角PQDA的余弦值为,求四面体ADPQ的体积.
解析:由题设知,AA1,AB,AD两两垂直,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A(0,0,0),B1(3,0,6),D(0,6,0),D1(0,3,6),Q(6,m,0),其中m=BQ,0≤m≤6.
点评:本题是一道立体几何逆向题.通过设定变量m,λ利用二面角PQDA的余弦值为以及PQ∥平面ABB1A1的条件建立等量关系,求出变量m,λ的值,体现了方程的思想.
3.3运用函数的思想解决立几中的最值问题
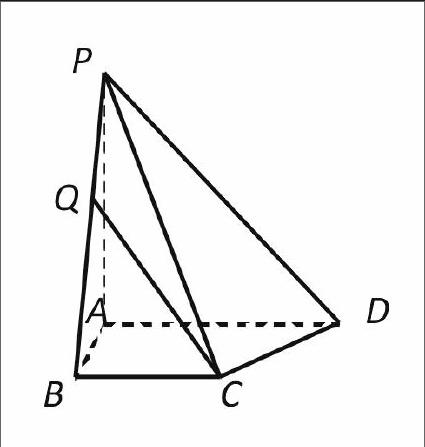
例题3.3. 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成角最小时,求线段BQ的长.
解析:以{,,}为正交基底建立如图所示的空间直角坐标系A-xyz,则各点的坐标为B(1,
总之,作为高中数学基础知识的重要内容,数学思想与数学方法属于教学中的重点,也是学生学习过程中的难点.通过思想与方法的学习能够真正理解数学的价值和意义.函数与方程的思想是高中数学的基本思想方法之一,也是高考的重中之中,是掌握许多数学知识的基础. 运用函数与方程的思想方法去解题,才举一反三,融会贯通,才能俯瞰题目,达到“一览众山小”的境界.函数与方程思想的运用在高中数学中无处不在,在解题中应注意体会,归纳总结,形成方法和能力.
责任编辑 徐国坚

