轮履变换车辆主动轮与履带板啮合损耗分析

苏 杰， 李春明， 范知友

(中国北方车辆研究所，北京 100072)

轮履变换车辆主动轮与履带板啮合损耗分析

苏 杰， 李春明， 范知友

(中国北方车辆研究所，北京 100072)

为研究轮履变换车辆主动轮与履带板啮合的损耗变化，首先结合轮履变换车辆结构，对其进行受力分析；然后采用Matlab和RecurDyn建立了主动轮与履带板啮合数学模型和多体动力学仿真模型；最后，仿真分析了该车辆在轮式状态和履带状态下，分别在硬质路面上以10 km/h、20 km/h、30 km/h、40 km/h、50 km/h匀速行驶一段时间内的主动轮与履带板啮合的功率损耗，结果表明，该车辆在轮式状态下匀速行驶时，其主动轮与履带板啮合的功率损耗低于履带状态，特别是在轮式状态下以40 km/h匀速行驶时，其主动轮与履带板啮合的功率损耗比在履带状态下匀速行驶时减少了36.49%.

履带车辆；变形轮；主动轮；张紧力；摩擦损耗

履带车辆的行驶环境复杂多变，对各类地形都有良好的适应能力才能满足多元化的使用需求.一方面，要求履带车辆要有复杂地域和恶劣路况下的通过能力；另一方面，要求车辆要有硬路面的高速行驶能力，从而利于车辆在公路、城市等环境下的快速反应和灵活机动.履带装置可以提高车辆对地形的适应能力，但其高速行驶时摩擦损耗大.为提高履带车辆机动性能，变形轮技术得到广泛应用.王东亮等作者提出了一种变形轮行走机构设计方案[1]，兼有轮式行走机构高速性和履带式行走机构高通过性特点，该结构具有借鉴意义，但受限于承载能力，其设计无法适用于重型车辆.美国Inuktun公司的履带可变形侦察机器人(VGTV)[2]通过控制伸展摆臂的伸长与收缩改变履带的形状，实现履带接地面积可调，但由于行驶速度有限，无法实现高速机动.为满足重型履带车辆高机动性要求，对传统履带结构进行改进是实现履带车辆高速行驶的有效途径.通过轮履变换可实现履带环形运动，减小履带接地面积，降低行驶阻力，提高车辆高速性能.

履带车辆高速行驶时，主动轮与履带板啮合摩擦损失占据总功率损失的比重较大，因此，降低主动轮啮合摩擦损耗可以有效改善履带车辆行驶功率损耗.而履带张紧力是主动轮啮合损耗的重要影响因素，况且履带车辆在行驶时，履带张紧力呈剧烈波动状态，导致履带与主动轮之间的啮合摩擦损耗的波动[3].为实现履带车辆高速行驶性能，对履带的张紧力提出更高要求.履带张紧力过小容易导致履带“脱齿”现象的发生，张紧力过大会增加磨损，降低车辆的动力传递效率.履带张紧力是求解主动轮啮合摩擦力的前提，进而求解出啮合摩擦损耗.针对传统履带结构，袁芬等作者[4]针对传统履带结构提出了精确计算诱导轮张紧力的方法，并进行仿真验证，而肖永开等作者[5]建立履带车辆动力学模型，着重分析预张紧力对车辆行驶的影响.本研究参考上述张紧力计算和分析方法，针对变形轮结构建立动力学模型，求解主动轮啮合损耗.

1 动力学分析

车辆行驶时，作用在履带环上的力分为恒定力和交变力.恒定力包括预紧力、牵引力和离心力，产生履带张紧力的恒定分量；交变力包括履带、负重轮和车体的纵向和横向振动，由啮合不均匀和履带板块结构造成的动载荷，产生履带张紧力的可变分量[6].由于张紧力的可变分量难以计算，通常采取强度储备系数方式进行估算，现讨论履带环上张紧力的恒定分量.

1.1 履带环张紧力分布

轮履变换车辆的主动轮位于顶部，诱导轮和负重轮固定在可以调节的保持架上.通过调整保持架形状，实现轮履转换，高速行驶时为轮式状态，如图1所示；越野行驶时为履带状态，如图2所示.

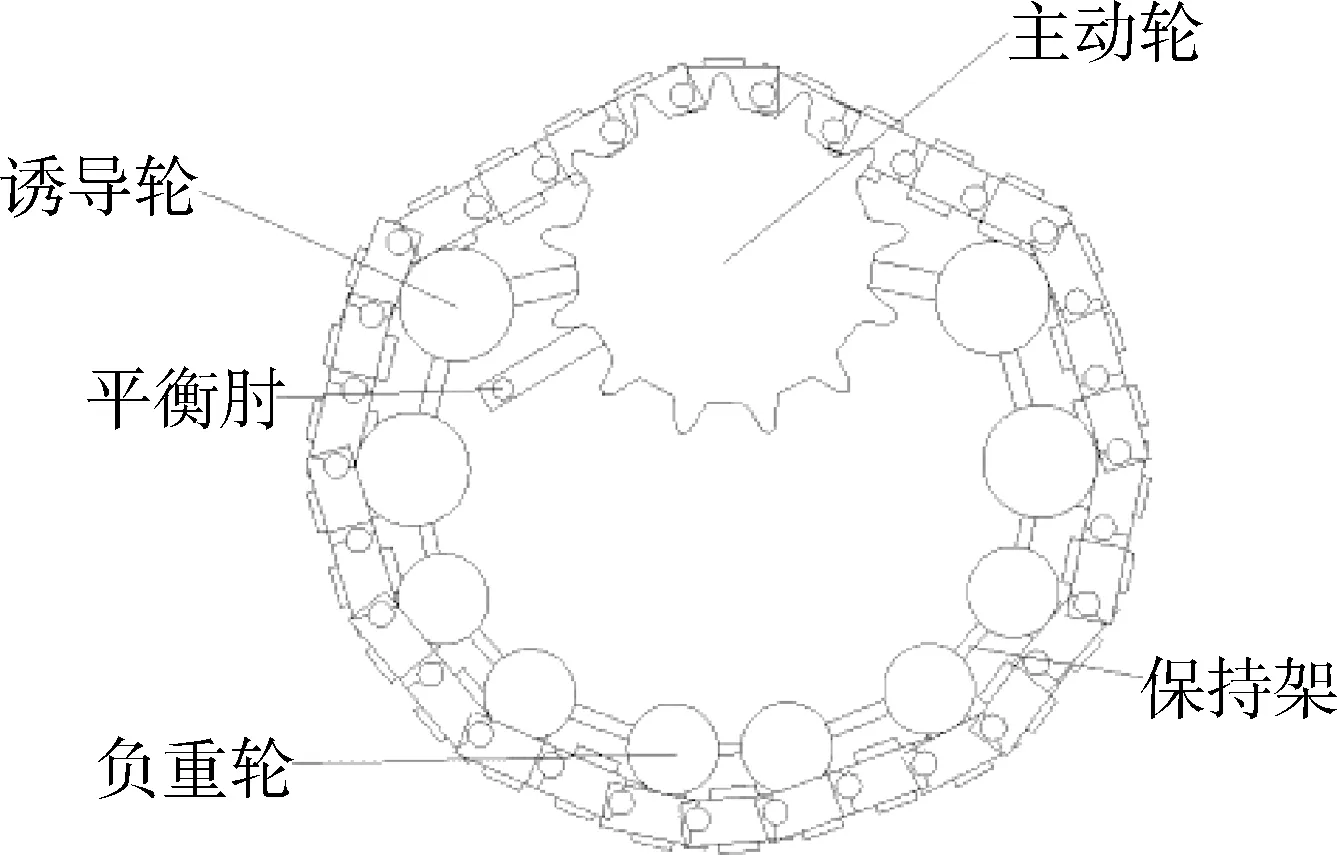
图1 轮式状态结构图

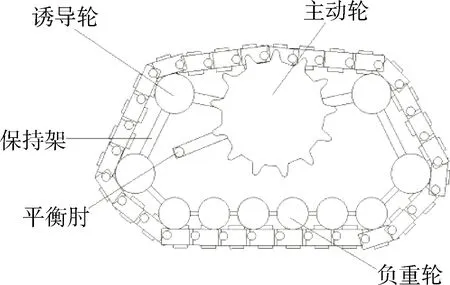
图2 履带状态结构图

如图3和图4所示，将履带环分为三部分：工作段、非工作段、接地段

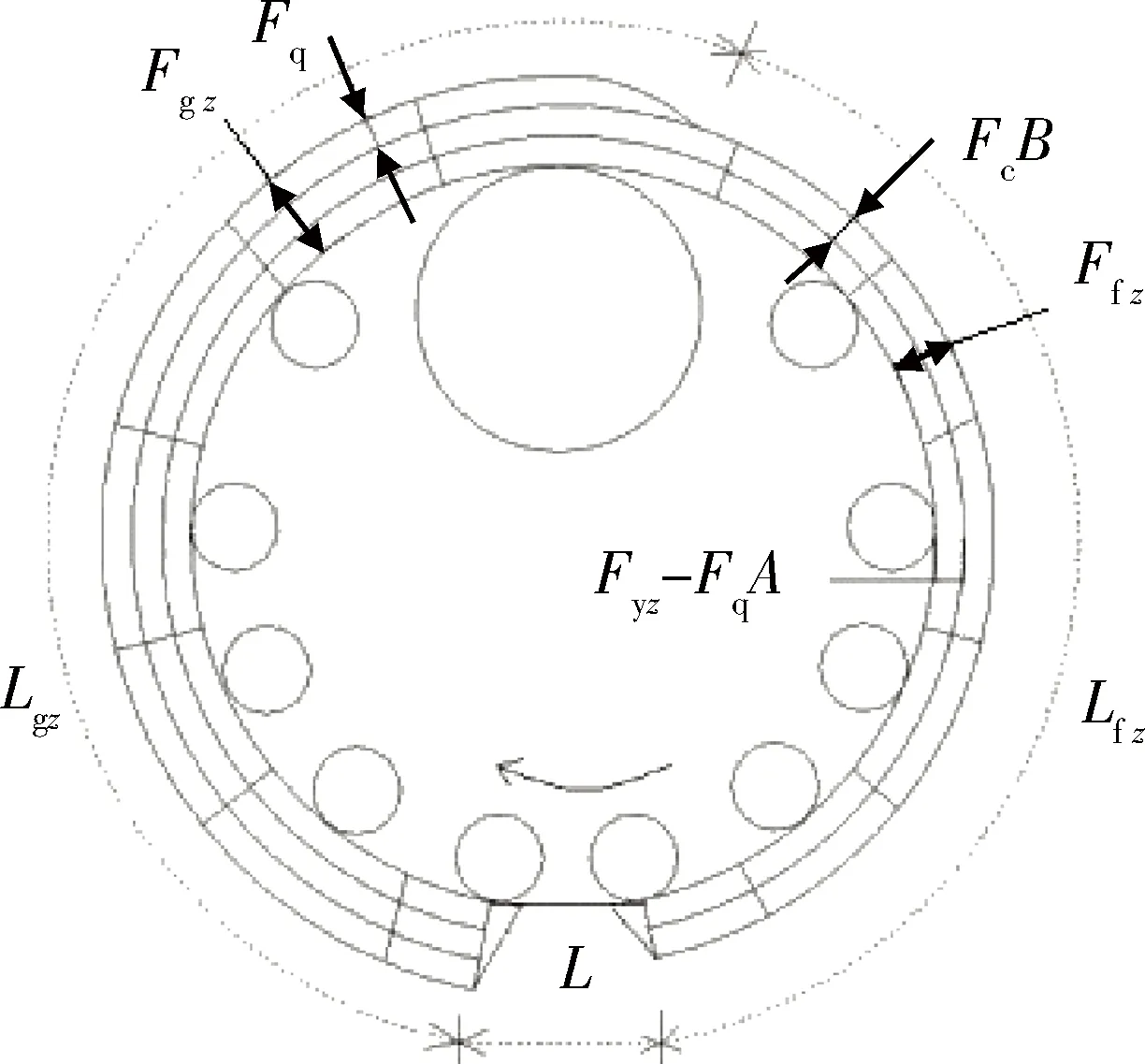
图3 轮式状态张紧力分布情况

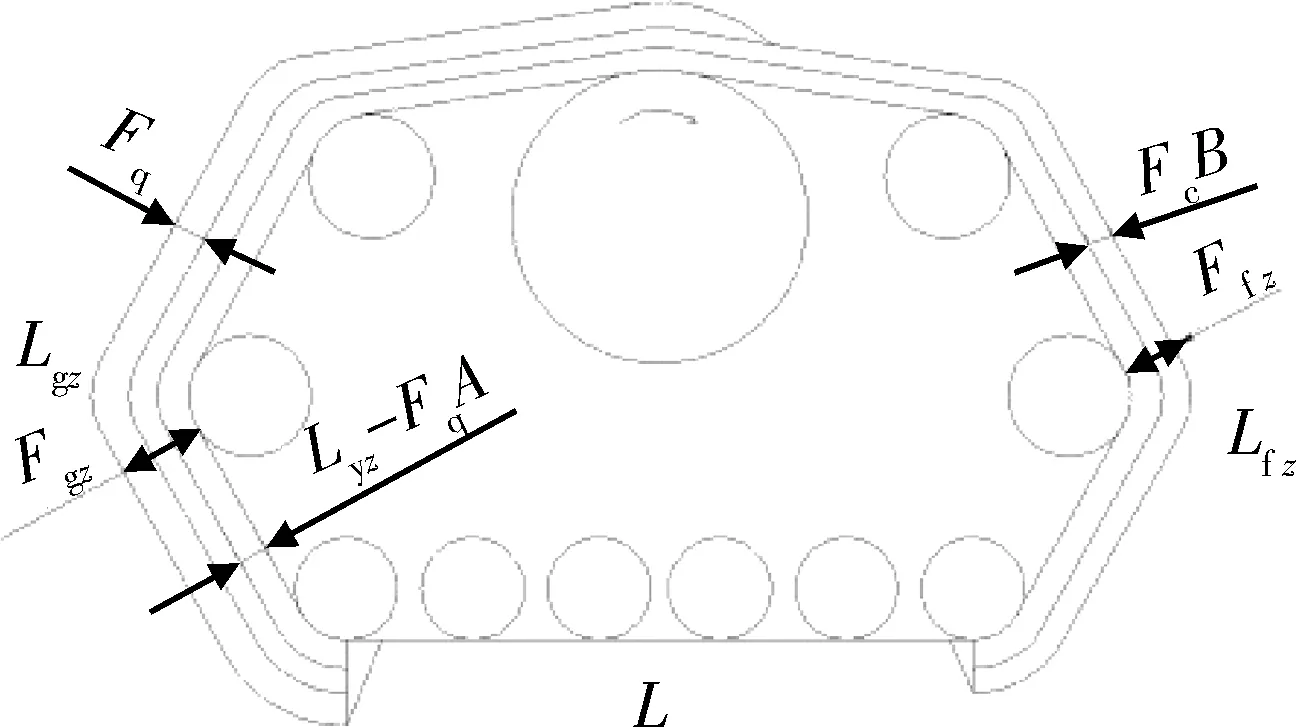
图4 履带状态张紧力分布情况

图中，Ffz为非工作段张紧力：

Ffz=Fyz-FqA+FcB，

(1)

A=1/(1+Lgz/Lfz),

(2)

B=K/(1+K).

(3)

式中：Fq为主动轮所产生的驱动力；Fc为履带板位移方向变化产生的离心力；Fyz为履带预紧力；K为履带挠度和行驶部分结构的参数，对于挂胶履带行驶装置来说，K=0.2～0.5.

工作段张紧力Fgz包括非工作段张紧力和主动轮驱动力.

Fgz=Fyz+Fq(1-A)+FcB.

(4)

考虑到履带与负重轮、诱导轮、主动轮以及履带链节之间的摩擦力影响，引入影响系数Kd.对于有拖带轮的行动装置和有预加扭转角的履带，Kd=2.

则离心张紧力Fc为

Fc=0.03Kdmdv2.

(5)

式中：md为履带的单位长度质量；v为车辆行驶速度.

1.2 主动轮动力学分析

主动轮处受力情况如图5所示，履带板相对转动角度如图6所示.

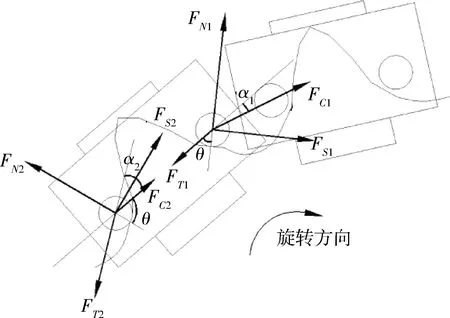
图5 主动轮处受力情况

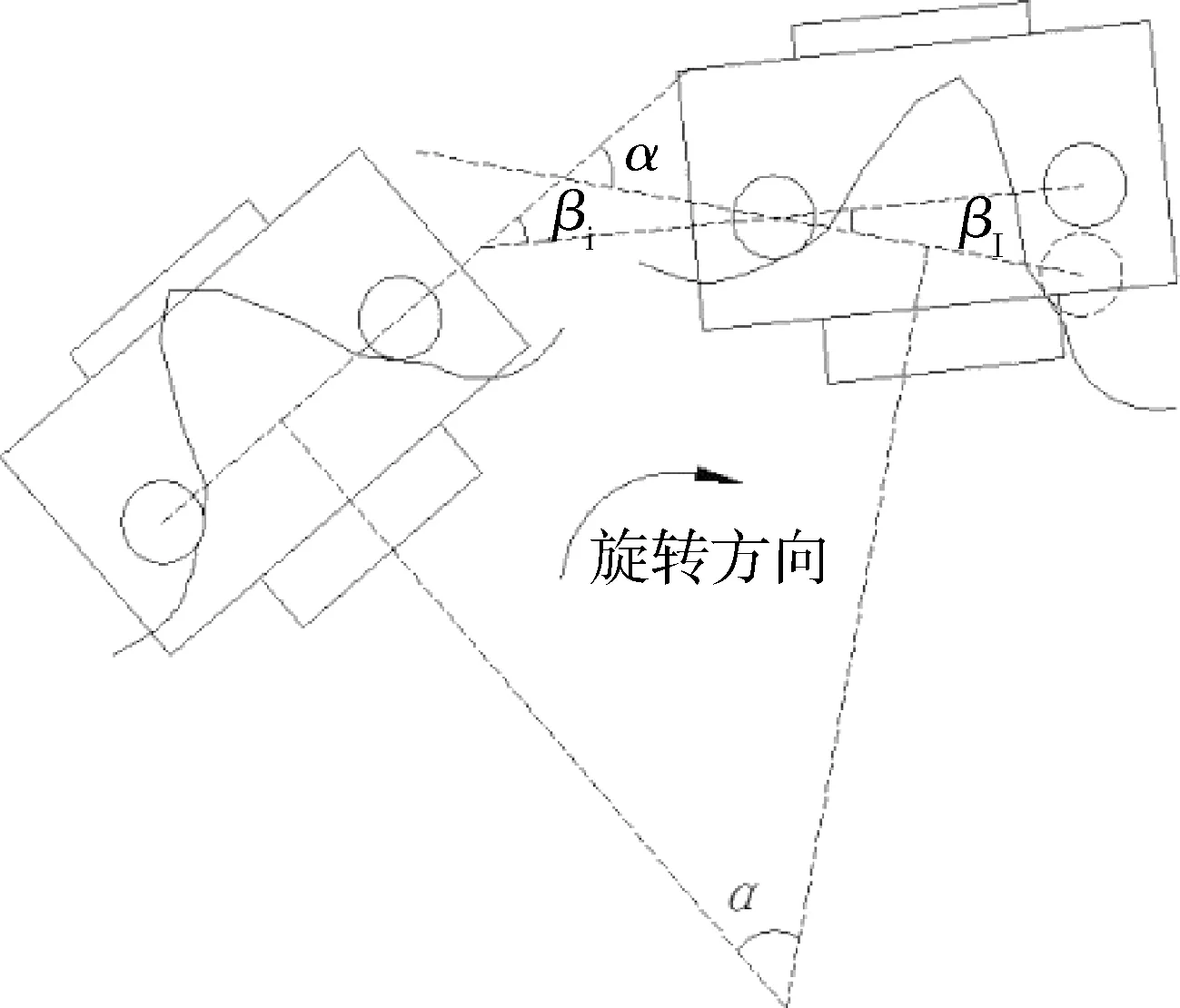
图6 履带板相对转动角度

对于进入啮合的履带板的第1个履带销，其受力平衡方程为

FN1+FC1cos(α1+θ)-FT1cosθ=0

,

(6)

FS1+FC1sin(α1+θ)-FT1sinθ=0

,

(7)

FS1=μ1FN1.

(8)

对于第2个履带销，其受力平衡方程为

FN2+FT2cos(α2+θ)-FC2cosθ=0

,

(9)

FS2-FT2sin(α2+θ)-FC2sinθ=0

,

(10)

FS2=μ1FN2.

(11)

联立以上各式可得：

(12)

(13)

(14)

(15)

式中：θ为压力角，即啮合点的法线与传力的相邻履带销中心的夹角；α1为双销履带绕过主动轮时，前端联器相对履带板的转角；α2为履带板相对于后端联器的转角；μ1为摩擦系数，钢与钢摩擦可取0.16.

FC1和FC2为履带销松边张紧力，FT1和FT2为履带销紧边张紧力.在加速和匀速前进时，前一个履带销的紧边是后一个履带销的松边，即

FT1=FC2.

(16)

对于第1块进入啮合的履带板，FT1即为整条履带中的工作段履带张紧力.

FT1=Fgz=Fyz+Fq(1-A)+FcB.

(17)

在实际行驶中，由于受路面不平度和履带与地面间的摩擦力的影响，履带工作段张紧力并不是预紧力、离心力和牵引力的简单相加，因此需要建立履带张紧力动力学模型进行详细分析计算.

1.3 主动轮与履带板啮合摩擦功率损耗

对主动轮进行动力学分析，可得主动轮与履带板啮合传力过程中，履带销在主动轮齿圈表面的相对滑动产生的功率损耗P1.

(18)

s=rβ1，

(19)

β1=α-βi.

(20)

式中：s为履带销与主动轮齿圈相对滑动位移；t1为啮合过程时间；r为履带销半径；β1为履带销滑动相对转角，等于履带板转角βi与主动轮齿圈转角差值.

由以上各式可得摩擦功率损耗：

(21)

式中：ω0为主动轮转速；ωi为履带板转动角速度.

2 虚拟样机仿真

2.1 RecurDyn功能介绍

履带车辆行驶过程包含动态载荷、接触损耗、冲击碰撞等情况，是一个复杂的多刚体系统动力学问题，传统动力学仿真软件难以准确求解摩擦损耗.与其他同类型软件相比，RecurDyn具备分析复杂多体动力学问题的优势，在履带车辆动力学分析方面优势更加明显.RecurDyn软件提供了高速履带模块(High Track)和低速履带模块(Low Track)，包括常用的实体和元素，同时提供履带板和路面轮廓库.模型库中预设多种类型车轮结构，如主动轮、拖带轮、负重轮.履带板结构包括单销式履带板和双销式履带板，在给定参数的情况下能够快速建立行动装置模型.该软件还增加了并行求解算法，改进原有的接触算法，提出了解析解接触算法、实体接触算法和针对柔性体的接触算法，以满足大型有限元多体动力学问题的计算需求.具备与Matlab/Simulink对接的能力，可以进行机械系统和控制算法的联合求解，并且针对各个行业设计多种不同接口，允许用户进行二次开发.

2.2 RecurDyn与Matlab联合仿真

针对轮履变换车辆采用轮毂电机驱动的结构，由于RecurDyn程序不提供电机驱动，仅能施加主动轮扭矩且拟真度较低，所以建立的虚拟样机缺乏真实准确的电机驱动及其控制策略.当以主动轮恒定转速为控制目标进行仿真分析时，扭矩波动与电机输出情况不匹配，并且无法有效计算行动系统功率损耗在电机输出功率所占的比值.因此利用RecurDyn的接口技术将虚拟样机模型和基于Matlab/Simulink建立的电机及其控制器模型结合起来，实现机械系统和控制系统的联合仿真.通过设定电机控制策略，在控制策略中引入主动轮转速反馈来保证车辆匀速直线行驶的稳定性，来模拟轮履变换车辆分别以10 km/h、20 km/h、30 km/h、40 km/h、50 km/h的车速匀速行驶时主动轮与履带板啮合的功率损耗情况.

2.3 车辆虚拟样机建立

根据轮履变换车辆的详细结构数据，基于RecurDyn的高速履带模块Track/HM建立车辆模型.如图7所示，该模型包括车身和6个履带轮.履带轮由主动轮、诱导轮、负重轮、保持架、悬挂装置、履带板、张紧装置组成.对各相对运动部件进行约束，按照设计参数设置悬挂装置扭转弹簧的刚度系数和阻尼系数、履带板的刚度系数和阻尼系数、张紧装置弹簧刚度和自由长度，通过调整张紧装置来改变履带预紧力.

图7 虚拟样机模型

2.4 运动学仿真分析

在实际行驶过程中，车体振动的根源是路面不平度，路面模型是否准确可靠会直接影响仿真结果[7].为了正确分析主动轮与履带板啮合摩擦损耗，需要构造合理的路面模型.鉴于本研究主要针对轮履变换车辆在硬质路面高速行驶工况的啮合摩擦损耗变化情况，故采用RecurDyn软件提供的平坦坚实硬地面进行仿真分析.RecurDyn中硬路面上履带板与地面之间的压力是通过履带接触(ground-track link shoe pad)来定义的，计算公式为F=-k(q-q0)n-cq,其中，q0为初始沉陷量，q为行驶沉陷量，k为地面刚度，c为地面阻尼，n为土壤变形指数，具体参数如表1所示.RecurDyn根据库仑定律Ff=fc·F实时计算履带与地面间摩擦力，进而求得履带张紧力、履带板转动角度等未知量.

表1 平坦坚实硬地面特征参数值

运行仿真程序，分别对轮式状态和履带状态进行分析计算，可以得到10 km/h、20 km/h、30 km/h、40 km/h、50 km/h五种不同车速下的履带张紧力、相邻履带板转动角度、主动轮与履带板啮合压力.使用公式(14)和公式(21)，按照图8所示的计算过程，可以求出各车速对应的主动轮与履带板啮合的摩擦损耗.

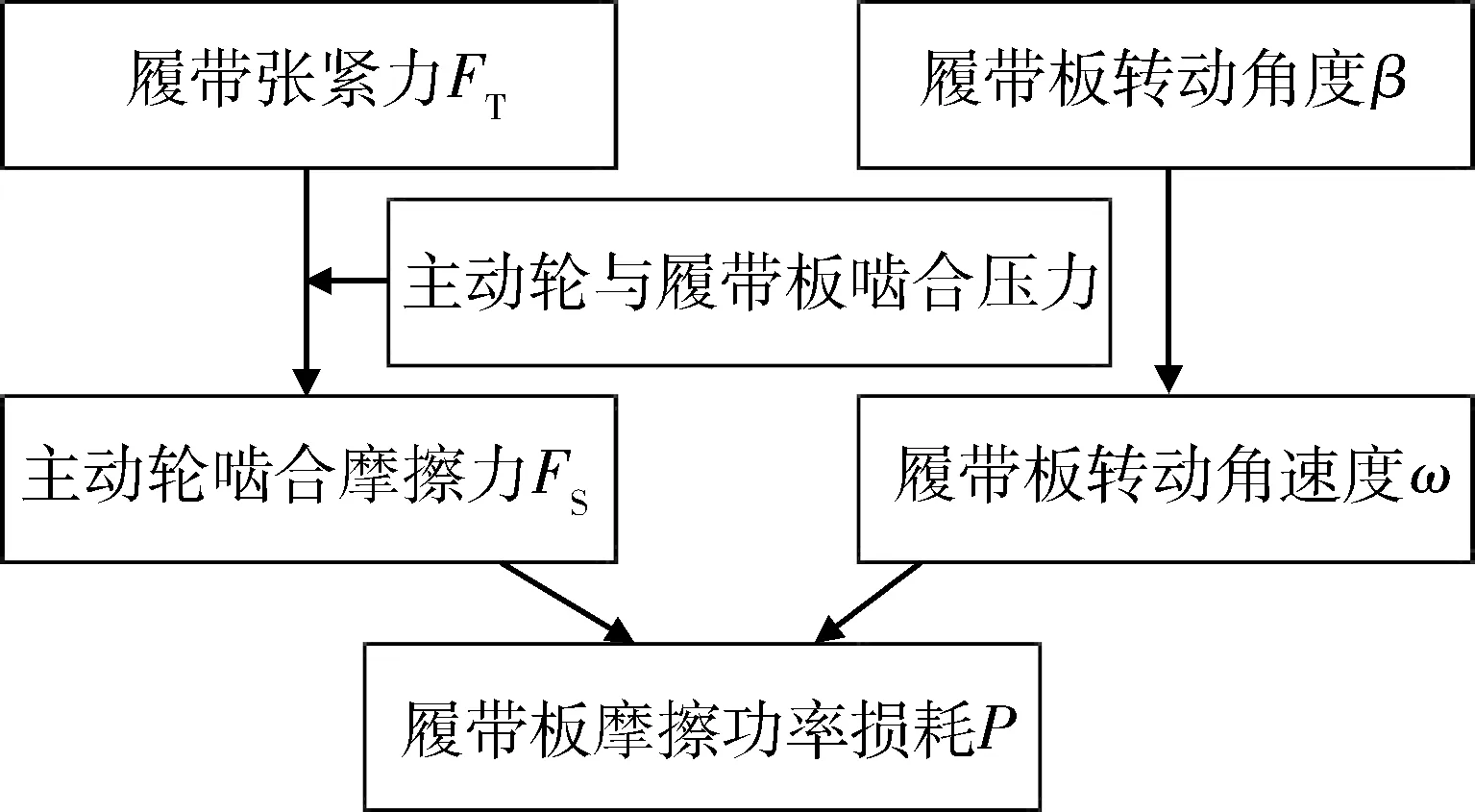
图8 计算流程图

图9为10 km/h时啮合摩擦功率损耗.由图9可以求得7 s至10 s匀速行驶时主动轮与履带板啮合的摩擦功率损耗平均值，轮式状态为33.09 W，履带状态为41.61 W.

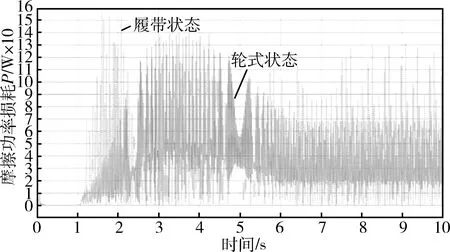
图9 加速至10 km/h时主动轮与履带板啮合的摩擦功率损耗

图10为20 km/h时啮合摩擦功率损耗.由图10可以求得7 s至10 s匀速行驶时主动轮与履带板啮合的摩擦功率损耗平均值，轮式状态为131.63 W，履带状态为157.65 W.

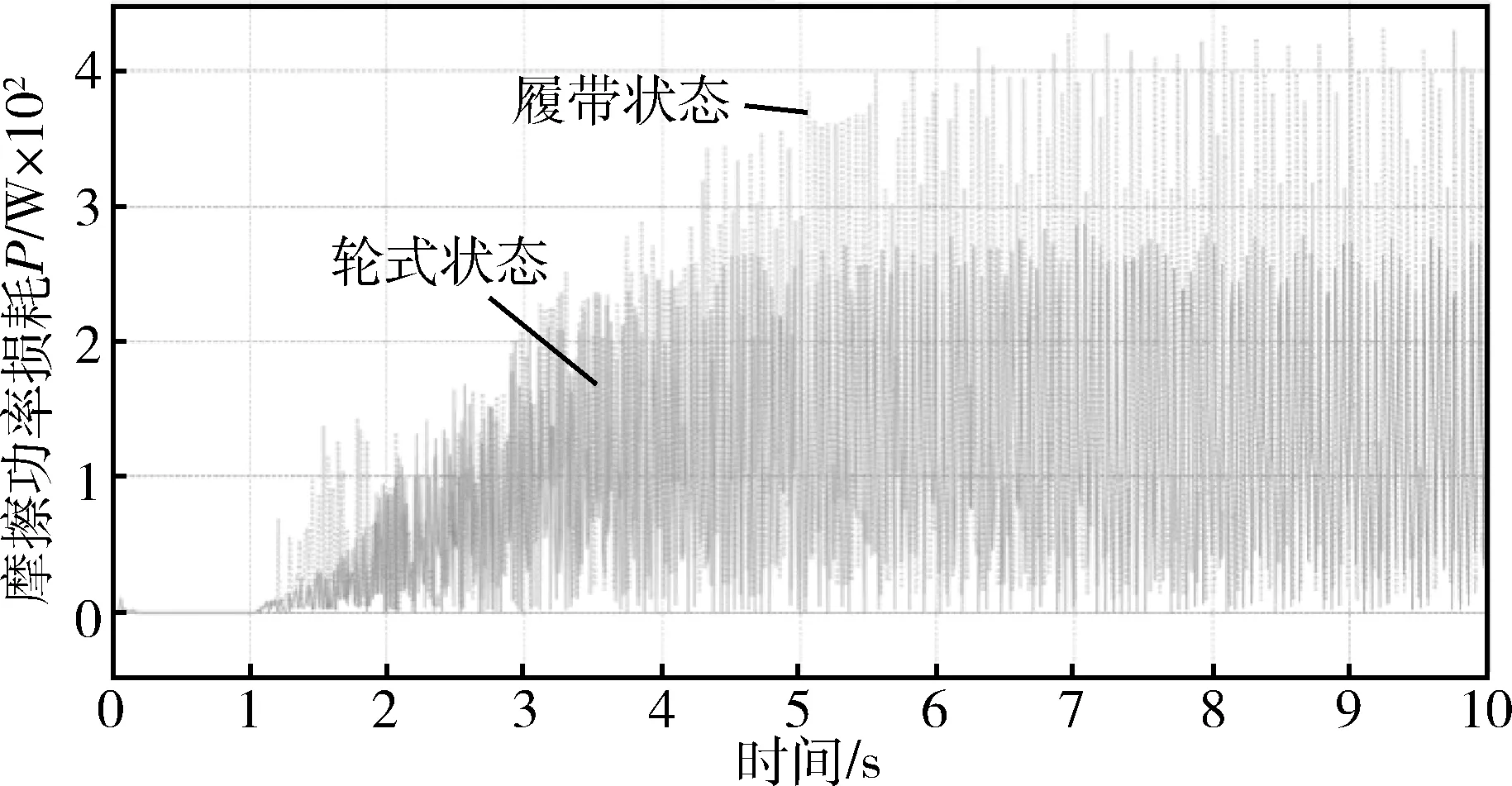
图10 加速至20 km/h时主动轮与履带板啮合的摩擦功率损耗

图11为30 km/h时啮合摩擦功率损耗.由图11可以求得7 s至10 s匀速行驶时主动轮与履带板啮合的摩擦功率损耗平均值，轮式状态为244.75 W，履带状态为299.86 W.

图11 加速至30 km/h时主动轮与履带板啮合的摩擦功率损耗

图12为40 km/h时啮合摩擦功率损耗.由图12可以求得7 s至10 s匀速行驶时主动轮与履带板啮合的摩擦功率损耗平均值，轮式状态为343.18 W，履带状态为540.33 W.

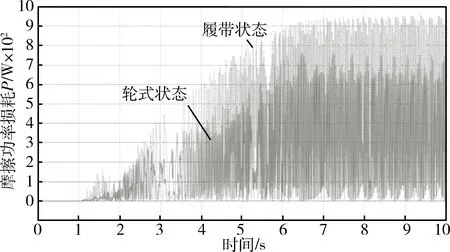
图12 加速至40 km/h时主动轮与履带板啮合的摩擦功率损耗

图13为50 km/h时啮合摩擦功率损耗.由图13可以求得7 s至10 s匀速行驶时主动轮与履带板啮合的摩擦功率损耗平均值，轮式状态为527.07 W，履带状态为769.51 W.

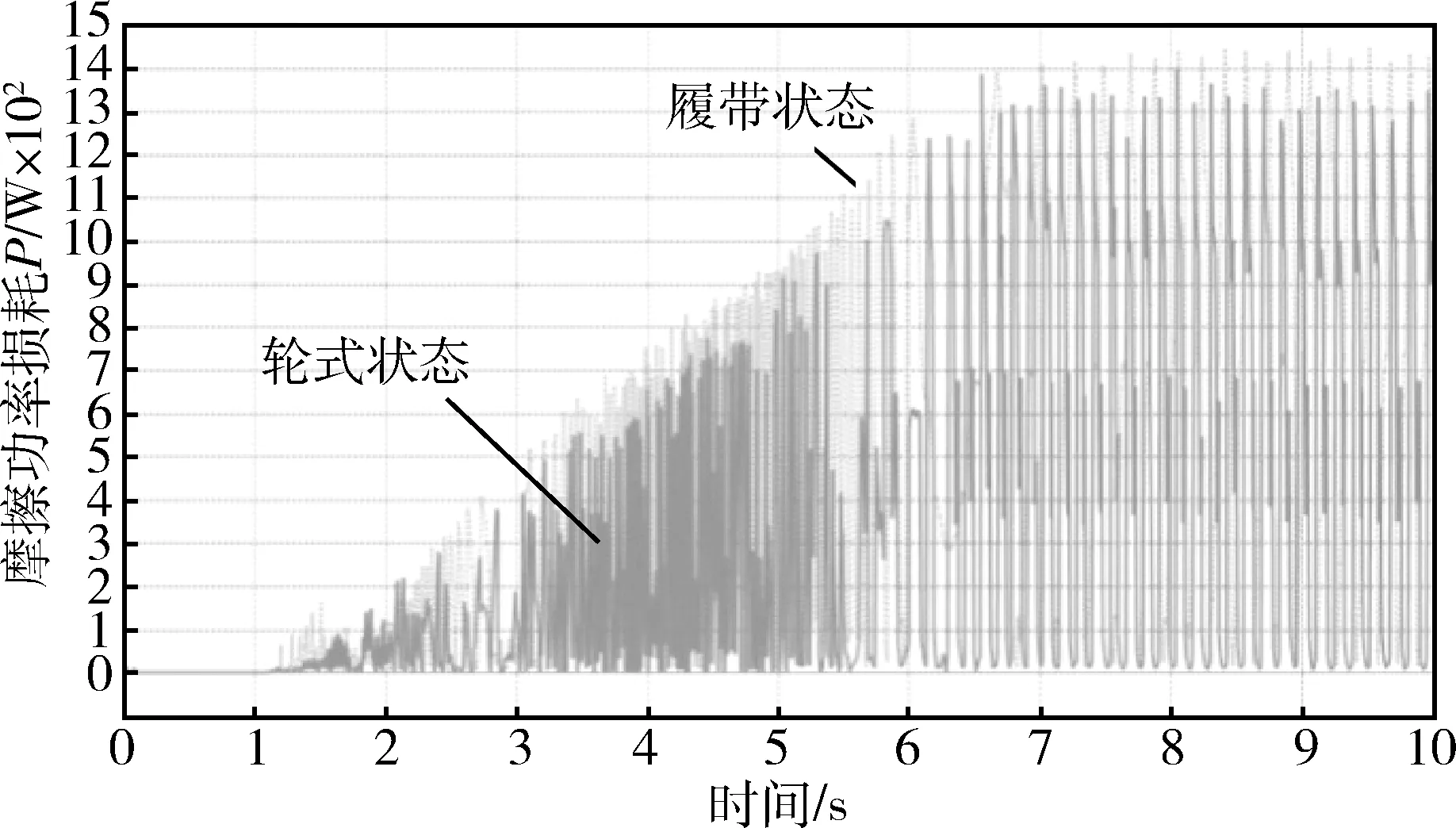
图13 加速至50 km/h时主动轮与履带板啮合的摩擦功率损耗

由于车辆在加速过程中主动轮与履带板接触情况复杂，驱动力变化快、幅度大，行动装置部件会产生剧烈的冲击碰撞，要准确计算加速过程中主动轮与履带板啮合的摩擦功率损耗比较困难，因此本研究是针对图9至图13中的7 s至10 s匀速行驶阶段的啮合摩擦损耗进行分析计算的.使用多项式对所得数据进行拟合，可以得到轮履变换车辆主动轮与履带板啮合的摩擦功率损耗与车速的函数关系，轮式状态为P=0.0059v3-0.4202v2+19.2487v-125.136，履带状态为P=-0.0031v3+0.5128v2-2.8912v+24.962.当轮履变换车辆在硬质路面以特定车速行驶时，可以使用该公式对车辆的主动轮与履带板啮合的摩擦功率损耗情况进行测算.

图14是根据函数关系绘制的曲线，可以看出：主动轮与履带板啮合摩擦功率损耗随着车速增加逐渐增加，车辆在硬质路面以10 km/h至40 km/h的速度行驶时，轮式状态损耗均小于履带状态，车速越高，轮式状态对啮合损耗的改善情况越明显；而以50 km/h的速度匀速行驶时，轮式状态对啮合损耗的降低幅度有所减少.如图12所示，车辆在硬质路面以40 km/h的速度匀速行驶时，轮式状态的主动轮与履带板啮合损耗比履带状态降低了36.49%，此时主动轮与履带板啮合的摩擦损耗的改善效果最明显.而车辆在硬质路面以50 km/h的速度匀速行驶时，如图13所示，轮式状态的主动轮与履带板啮合损耗比履带状态仅降低了31.51%.

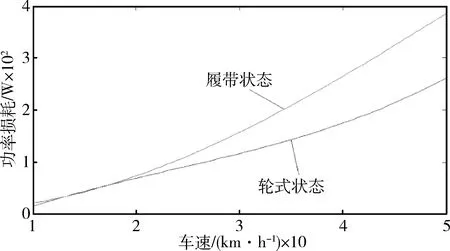
图14 主动轮与履带板啮合的摩擦功率损耗随车速变化

3 结 论

为改善履带车辆主动轮与履带板啮合的摩擦功率损耗情况，针对功率损耗大的问题，使用Simulink和RecurDyn进行联合仿真，对车辆在履带状态和轮式状态下分别以不同车速匀速行驶时主动轮与履带板啮合的摩擦功率损耗进行分析研究.研究结果表明，轮履变换车辆在轮式状态可以有效改善主动轮与履带板啮合的摩擦损耗情况，在40 km/h时啮合摩擦损耗降低36.49%.本研究未讨论车辆在加速过程中的主动轮啮合损耗情况，对土路、沙石路等软路面行驶工况下主动轮啮合损耗情况也有待进一步研究.

[1] 王东亮, 孙逢春, 程守玉. 一种新型变形轮行走机构研究[J]. 北京理工大学学报,2012, 32(1):33.

[2] Jeehong Kim, Changgoo Lee, Gunho Kim. Study of Machine Design for a Transformable Shape Single-tracked Vehicle System[J]. Mechanism and Machine Theory, 2010, 45(1):1082-1095.

[3] 刘 斌. 高速履带车辆推进装置的动力学特性研究[D]. 北京:北京理工大学,2015:23.

[4] 袁 芬, 张 明. 高速履带车辆诱导轮张紧力的计算与仿真[J]. 车辆与动力技术,2008,(1):44-50.

[5] 肖永开, 李晓雷. 高速履带车辆履带预紧张力对平顺性的影响[J]. 计算机仿真,2006,(7):253-255.

[6] 闫清东, 张连第, 赵毓芹. 坦克构造与设计(下)[M]. 北京:北京理工大学出版社, 2007: 517.

[7] 李 超. 履带车辆履带张紧力分析[D]. 北京:北京理工大学, 2012:50.

Analysis on Sprocket and Track Mesh Power Loss ofWheel-tracked Vehicle

SU Jie, LI Chun-ming, FAN Zhi-you

( China North Vehicle Research Institute, Beijing 100072, China)

In order to research the transformation of sprocket mesh power loss of wheel-tracked vehicle, loads analysis combined with wheel-tracked vehicle structure was conducted at first. Then mathematical models of sprocket and track were built. Multi-body dynamics simulation of wheel-tracked vehicle was conducted based on Matlab and RecurDyn.Finally, dynamic transformation of sprocket mesh power loss in the invariable speed process on hard road was analyzedat the speed of 10 km/h, 20 km/h, 30 km/h, 40 km/h and 50 km/h. The result indicated that the wheel state of wheel-tracked vehicle decreased the sprocket mesh power loss efficiently. Especially at the speed of 40 km/h, sprocket and track mesh power loss of wheel state is 36.49% less than that of track state.

tracked vehicle; deformable wheel;sprocket;tension; friction loss

1009-4687(2017)01-0015-06

2017-01-03.

苏杰(1992-)，男，硕士研究生，研究方向为车辆动力学.

TJ81+0.1；TJ81+0.33

A