基于迭代最邻近的多视角目标识别算法研究

刘洲峰, 赵亚茹, 李春雷, 王宝瑞, 刘超蝶

(中原工学院, 郑州 450007)

基于迭代最邻近的多视角目标识别算法研究

刘洲峰, 赵亚茹, 李春雷, 王宝瑞, 刘超蝶

(中原工学院, 郑州 450007)

针对传统图像识别视角单一问题，提出了一种改进的多视角目标识别算法，结合空间结构连续性，利用迭代最邻近算法ICP(Iterative Closest Points)进行多视角目标识别。首先，构建高斯尺度空间来提取具有尺度不变性的SURF(Speed-up Robust Features)特征点,得到特征描述子，且根据描述子的相似性得到初始转换参数；然后，将描述子相似性与空间结构连续性相结合，利用ICP求得匹配对，并进行配准；最后，在各个角度的图像中对目标图像进行识别，取得了较好的效果。实验结果表明，所提出算法识别效果显著，准确率高，具有很好的鲁棒性。

特征相似性；图像配准；局部结构限制；空间连续性

随着现代军事电子技术的不断发展，目标识别技术应运而生。目标识别可以提供目标属性、类别等信息，可以大幅度提高军队的攻防能力、国土防空反导能力和战略预警能力，可以广泛应用于军事目标识别和战场环境仿真。

特征点匹配作为目标识别的重要组成部分，决定了目标识别的精确度。目前常用的图像配准方法可以分为两类：基于区域灰度信息的方法、基于特征的方法。灰度信息配准利用图像灰度信息建立图像的相似性度量，从而进行图像配准。这种方法由于对灰度变化敏感，计算复杂度高，对目标的旋转和形变比较敏感，通常不单独用于遥感图像配准中实时性要求较高的场合。基于特征点的图像配准方法能够克服灰度信息配准的缺点，首先提取图像特征点，然后利用相似性度量方法进行特征匹配，建立图像间的映射关系，之后进行插值，得到配准结果[1]。特征点图像配准因速度快、计算量小、鲁棒性好等优点而得到了广泛的应用。但是，由于其图像采集过程仍然存在因空间转换、视角变换而产生的空间形变、灰度差异，因此图像配准还面临许多挑战。

为了应对这些挑战，需要选用对尺度变化、角度差异具有不变性的特征点进行图像配准，以达到稳定的配准效果，从而精确地对目标进行识别[1]。近年来，许多学者致力于研究图像配准技术，提出了许多图像配准方法。Zitová B等总结了图像配准的几种方法，并根据它们的特性和4个图像配准步骤(特征检测、特征匹配、映射函数设计、重采样)对图像配准的方法进行分类，最后陈述了这些方法的应用以及优缺点[1]。Scott G L等描述了如何联系两个图像的特征点，求得描述子的相似性程度[2]。Wen G J等引进一个独立变量作为匹配矩阵的目标函数，来描述两个特征之间的对应关系，且该对应关系是通过求取目标函数的最大值来确定的[3]。Li A等提出一种新的基于特征相似性和空间结构双向限制的图像配准方法，其中空间连续性不仅包括空间距离连续性，而且包括局部结构连续性[4]。

本文利用ICP(Iterative Closest Points)算法的框架和尺度不变的SURF(Speed-up Robust Features)特征点，结合描述子相似性和局部结构限制方法进行图像配准以达到最优匹配，用于多角度目标的识别。

1 图像配准方法

特征点图像配准包括特征点检测与描述、提取特征描述子、特征匹配、图像融合，其流程框图如图1所示。

图1 特征点图像配准框图

1.1 特征点检测与描述

特征点对图像匹配具有不同的鲁棒性。利用Mikolajczyk和Schmid提供的数据集进行测试，可得出在旋转变换、模糊变换、光照变换、尺度变换、视角变换等情况下鲁棒性均较高的SURF(Speed-up Robust Features)特征点[5-8]。SURF在重复度、独特性、鲁棒性3个方面的性能均超过或接近以往提出的同类方法，并且在计算速度上具有优势[9-10]。因此，本文采用SURF特征点进行配准。

1.2 特征匹配

给定一幅参考图像F和一幅待识别图像S，首先使用Hessian-Affine从F和S中提取关键点，利用SURF描述子对这些特征点进行描述，找到两幅图像中反映相同物理位置的特征点的对应关系。然后用特征描述子相似性SSD(Sum of Squared Differences)进行匹配,得到匹配点对的坐标点集。其匹配准则为最近距离与次近距离的比值不超过阈值thresh。按上述匹配准则进行特征点匹配，可以避免因尺度信息不同造成的图像中没有对应点却检测出匹配点对及描述子距离最近点不是匹配点的误匹配现象。

若DescriAi和DescriBi是任意两点A和B的描述子向量，则A、B两点之间的距离D可表示为:

(1)

用ND表示最近距离，NND表示次进距离，则距离之比Rod=ND/NND。若Rod小于阈值thresh则匹配成功，否则，匹配失败，即：

(2)

1.3 转换参数估计

假设有参考图像F和待拼接图像S，需要对两幅图像的特征点进行检测与描述，然后通过特征匹配得到匹配点对。计算过程中可能存在误匹配现象，需要剔除误匹配点(外点)来减少错误匹配。可利用随机抽样一致性算法(M-estimatorSampleConsensus，MSAC)将匹配对中的外点剔除，计算两幅图像的转换矩阵，得到初始的转换参数。如果最后得到的匹配对的数量大于2，则进行下一步匹配，否则匹配失败。

2 改进的目标识别算法

本文将描述子相似性与空间连续性相结合，利用双向匹配准则进行匹配，并且用MSAC去除误匹配对，最终实现目标识别。算法可分为初始转换参数估计、匹配矩阵求解、双向限制匹配、目标识别四大部分。算法的流程框图如图2所示。首先，根据特征匹配得到的匹配点对求得初始转换参数，并利用MSAC去除误匹配点；然后，根据每个图像的局部结构限制求得各自的空间连续性，并将特征相似性与空间连续性相结合，求得各自的匹配矩阵；接着，按照双向匹配准则求得最终的匹配矩阵，得到匹配特征点集；最后，计算出最终转换参数，将参考图像转换到待识别图像所在的坐标系，在待识别图像上标记出参考图像，即为目标。

图2 算法流程框图

2.1 空间连续性

根据文献[11]，引入LE算法来描述两幅图像间空间结构的相似性。

以参考图像为例，fi与fk都是参考图像F中的特征点，权重矩阵W中的元素表示特征点fi与fk的相近程度。如果fk为fi的k近邻点，则wik>0,否则wik=0。

那么，局部结构限制可以描述如下：

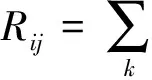
(4)

(5)

引入高斯核进行平滑，可优化如下：

(6)

同理，根据待识别图像的局部结构限制可以求出待配准图像的空间连续性，即：

(7)

2.2 转换参数

描述子相似性矩阵的计算过程可能存在误匹配现象，MSAC是RANSAC的变形。因此，可利用MSAC将匹配对中的外点剔除(阈值设为4)，计算两幅图像的转换矩阵，得到初始的转换参数[12]。如果最后得到的匹配对的数量大于2，则进行下一步匹配，否则匹配失败。

2.3 匹配矩阵

假设f={f1,f2,f3,…,fNF}为参考图像F的特征点集，s={s1,s2,s3,…,sNS}为待识别图像S的特征点集，NF和NS是特征点的个数，fi为第i个参考点，sj为第j个参考点。引入一个函数，它的独立变量是一个匹配矩阵，一旦待识别图像被完全转换到参考图像所在的坐标系中，最佳的匹配效果便可通过求取以下目标函数的最大值获得：

(8)

式中：M为匹配矩阵；Q为F和S的相似性测度矩阵。为了稳固地建立参考图像与待识别图像特征点之间的对应关系，需要将特征相似性与空间连续性相结合，求得相似性测度矩阵Q。假设特征相似性矩阵为C，且D为空间连续性矩阵，则Q=D·C。根据得到的初始转换参数，利用迭代思想可求得最优解。为了忽略两幅图像的不对等限制，将得到的匹配矩阵M增加一行一列，来解决匹配点对中具有外点的问题，增加的元素为0。有：

(9)

(10)

(1)初始化β=0.3。

(11)

(3)通过迭代得到最优的匹配矩阵M。

匹配矩阵M的收敛条件为：

(12)

式中，ε0=0.05。

(13)

(14)

增加β进行迭代，使β=β/0.9，再次有：

(15)

匹配矩阵的求解步骤结束。

2.4 双向匹配

3 实 验

为了验证本文算法的性能，本文选择的实验平台为MATLAB2016，利用从Google Earth上得到的高楼图像进行实验。其中一幅高楼图像与地面成90°方向(见图3)，另外几幅作为待识别图像，与目标物体成不同角度方向(见图4)。需要利用算法在待识别图像中找到参考图像。

图3 参考图像

(a) (b) (c) (d)

(e) (f) (g) (h)图4 待识别图像

将改进算法与现有算法进行对比，得到的对比结果如表1所示。从表1以及大量实验结果可以看出，本文算法在垂直方向一定的角度内能够得到更多的匹配点对。因此，本文算法比利用SURF进行目标识别的精确性更高。

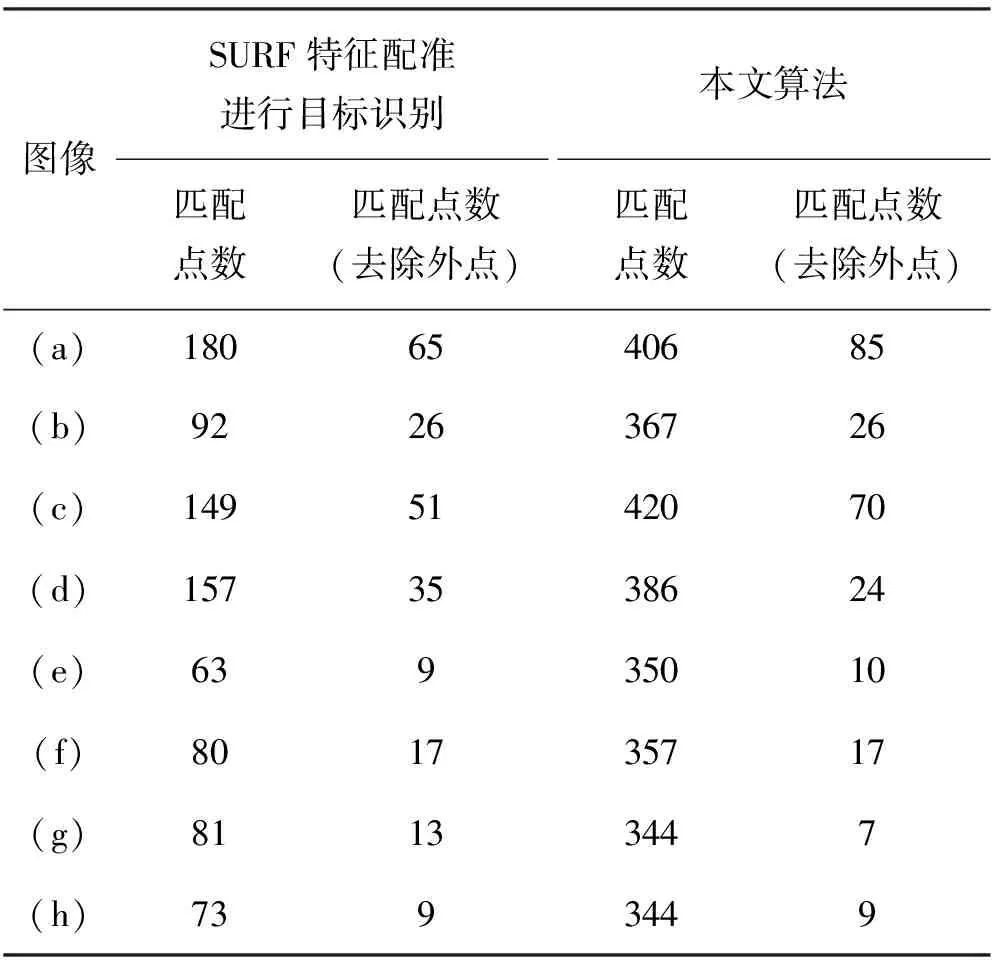
表1 改进算法与原算法对比

本文选取的图像包含100组不同目标的图像，匹配误差为0.730 9个像素。实验结果如图5所示。从图5左边数起，第一列为待识别图像，第二列为将待识别图像转换到参考图像所在坐标系所得到的配准结果图像，第三列为目标识别结果。

图5 实验结果

4 结 语

SURF特征点对平移、旋转、缩放均有一定的不变性。本文在结合特征相似性与空间连续性的基础上，对配准算法的框架和其中参数进行改进，并利用MSAC剔除误匹配点，对目标进行识别。通过大量实验对目标识别结果进行测试和评估。实验结果表明，本配准算法的精确性高、鲁棒性强，能够有效地进行目标检测，且算法运行效率较高。

[1] Zitová B, Flusser J. Image Registration Methods: A Survey[J]. Image & Vision Computing, 2003, 21(11):977-1000.

[2] Scott G L, Longuet-higgins H C. An Algorithm for Associating the Features of Two Images[J]. Proceedings of the Royal Society B Biological Sciences, 1991, 244(1309):21-26.

[3] Wen G J, Lv J J, Yu W X. A High-Performance Feature-matching Method for Image Registration by Combining Spatial and Similarity Information[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(4):1266-1277.

[4] Li A, Cheng X, Guan H, et al. Novel Image Registration Method Based on Local Structure Constraints[J]. IEEE Geoscience & Remote Sensing Letters, 2014, 11(9):1584-1588.

[5] 索春宝, 杨东清, 刘云鹏,等. 多种角度比较SIFT、SURF、BRISK、ORB、FREAK算法[J]. 北京测绘, 2014(4):23-26.

[6] Leutenegger S, Chli M, Siegwart R Y. BRISK: Binary Robust Invariant Scalable Keypoints[J]. Iccv, 2011, 58(11):2548-2555.

[7] Rublee E, Rabaud V, Konolige K, et al. ORB: An Efficient Alternative to SIFT or SURF[C]// IEEE International Conference on Computer Vision. Washington:IEEE, 2011:2564-2571.

[8] Ortiz R. FREAK: Fast Retina Keypoint[C]// IEEE Conference on Computer Vision and Pattern Recognition. Washington:IEEE Computer Society, 2012:510-517.

[9] Bay H, Tuytelaars T, Gool L V. SURF: Speeded Up Robust Features [J]. Computer Vision & Image Understanding, 2006, 110(3):404-417.

[10] Rangarajan A, Mjolsness E, Pappu S, et al. A Robust Point Matching Algorithm for Autoradiograph Alignment[J]. Medical Image Analysis, 1996, 4:379-398.

[11] Belkin M, Niyogi P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation[J]. Neural Computation, 2003, 15(6):1373-1396.

[12] Wang Z, Wang Z, Liu H, et al. Scale-invariant Feature Matching Based on Pairs of Feature Points[J]. Iet Computer Vision, 2015, 9(6):789-796.

(责任编辑：王长通)

Multiple View Object Recognition Based on Iterative Closest Points Framework

LIU Zhou-feng， ZHAO Ya-ru, LI Chun-lei, WANG Bao-rui, LIU Chao-die

(Zhongyuan University of Technology, Zhengzhou 450007, China)

Object recognition plays a great role in machine vision. Traditional image recognition just considers only viewpoint. An object recognition system has been developed in this paper. Firstly，Gaussian scale space is built to extract scale invariant feature points, and the SURF descriptor is utilized to characterize those feature points and get the transformation parameters. Then, feature similarity is combined with spatial consistency based on the iterate closest point. Finally, object is recognized in multiple view. Comparative experiments show that the algorithm has high performance in accuracy and robustness.

feature similarity; image registration; local structure constraints ;spatial consistency

2016-12-27

河南省科技攻关计划项目(132102210058)；河南省教育厅科学技术研究重点项目(13A510123)

刘洲峰(1962-)，男，河南原阳人，教授，博士,主要研究方向为智能信息处理与识别。

1671-6906(2017)01-0073-05

TP416;TN959.17

A

10.3969/j.issn.1671-6906.2017.01.016