函数与方程思想在高中数学解题中的应用

栾秀平，崔贤顺，朴勇杰

(1.延边大学 理学院，吉林 延吉 133002；2.延边第一中学，吉林 延吉 133001)

函数与方程思想在高中数学解题中的应用

栾秀平1，崔贤顺2，朴勇杰1

(1.延边大学 理学院，吉林 延吉 133002；2.延边第一中学，吉林 延吉 133001)

函数与方程思想在高中数学解题中有着重要的作用，针对函数与方程思想的概念，通过对高中数学中数列、实际问题、三角函数等模块进行具体的分析，探讨更利于学生学好数学的思想方法，以提高学生的学习质量和解题速率。

函数与方程思想；高中数学；解题应用

一、引言

数学方法是从量的方面展示数学作为科研工具的一种规律性的科学方法。究其本质而言，抽取出各种量以及量的变化和各量之间的联系，从而将研究对象与其他特性分离开来，最终形成对研究对象的数学解释和推理。数学方法是为数学解题而服务的，因而找到恰当的解题方法去处理相应的数学问题是十分必要的。数学方法是通过不断的实践积累推导运算产生的。就数学方法的高度抽象性、逻辑性、精确性、随机性特点而言，可以说数学方法是数学思想的另一种表达形式，通常称为“数学思想方法”[1]。

函数思想，是高考数学中重要的解题思想方法，利用灵活多变的手段，合理地分析数学中各种数量之间的联系，建立起相应的数学模型和各类函数干系，最终用函数思维和概念去解决问题。

方程思想，是从给定问题的条件开始着手，利用合理的数学语言将抽象的数学问题转化为通俗易懂的数学模型，运用数学中列方程解方程、列不等式解不等式使问题得到解决。

函数与方程思想，即是学会用函数和参数来思考，建立已知与未知之间的联系，对函数与方程的考核，首要看是不是能运用函数与方程思想去解题。针对实际问题，合理转化函数和方程，这类思想叫做“函数与方程思想”。

二、函数与方程思想的应用

1.函数与方程思想在数列中的应用

从数列与函数的观点看问题，可以给人以直观的表达，数列是函数的一种特别表达方式。数列与函数的关系并不仅是含义相似，更大的意义是数列本身具有的函数意义，运用函数思想可使许多数列问题迎刃而解。

例1：设数列{an}的前n项和为sn，满足sn=2nan+1-3n2-4n，n∈N*，且S3=15。

(1)求a1,a2,a3的值；(2)求数列{an}的通项公式。

解得a1=3,a2=5,a3=7

(2)因为sn=2nan+1-3n2-4n

①

所以当n≥2时，

sn-1=2(n-1)an-3(n-1)2-4(n-1)

②

最后用数学归纳法证明得到，综上所述，∀n∈N*，an=2n+1。

评注：函数与方程思想是一种运算策略，使问题中各个数量关系紧密地结合在一起，成为一个不可分割的整体，建立起恰当函数关系式，等式运算直指结论。同时也可以减少过程量，提高准确率，也使解题过程得到了升华，这对求解此类数列题型都具有必然的参考方向[2]。

2.函数与方程思想在现实问题中的运用

在高中数学中，以现实社会生产、生活问题为背景的数学应用题愈来愈受到关注，教学中要引导学生学会用函数与方程思想来解决生活中各类题型，提高学生的解题能力。

例2：某班20名孩子在一直线公路一侧植树，每人植一棵，相邻两棵树相距10米，开始时需将树苗集中放置在某一树坑旁边，现将树坑从1到20编号，为使列位学生从各自树坑前领取树苗所走的距离总和最小，树苗可以放置的两个最佳的编号为( )。

A.(1)和(20)B.(9)和(10)

C.(9)和(11)D.(10)和(11)

试题分析：设树苗可以放置的树坑编号为x，并列出此时学生从各自树坑前来领取树苗所走的距离总和，由绝对值性质，联系二次函数的知识便可获得树苗位置的最佳坑位的编号。

评注：本题考查的重点是函数最值的运用，其中包含绝对值的含义，运用函数与方程思想将现实问题转化为函数方程解答，我们将求一个绝对值函数最值知识，变成二次函数的最值知识，通过利用函数方程思想把复杂的问题简单化，从而使问题得到解决。

3.函数与方程思想在三角函数中的运用

三角函数是高中数学的重要知识，在三角函数中，运用方程(函数)思想解决求值、证明及研究三角函数性质，可使复杂的三角函数问题转变成简单的代数问题。

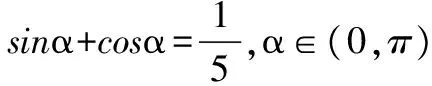
解析：由已知得:

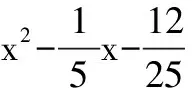
因为x∈(0,π)，sinαcosα<0

评注：本题考查的知识点为三角函数的求值知识，根据三角函数变量之间的联系，建立起求解一元二次方程根的代数式，从而使三角函数问题转化为学生熟悉的一元二次方程求根形式，使难懂的问题简单化。

三、小结

函数与方程思想在高中数学解题中具有重要的地位。函数描画了自然界中数量之间的联系，对于具体问题，构建函数恰当的数学模型，挖掘题目中的隐含条件，建立起函数表达式，准确表达函数的意义，是运用函数思想的精髓。学生如若掌握了这种数学思想，对他们解决高中许多数学问题一定会有很大的帮助，并能有效地提高解题效率，对培养学生观察、分析、理解、判断问题有一定的帮助，从而也节约了时间和精力[3]。

[1]邵光华.作为教育任务的数学思想与方法[M].上海：上海教育出版社，2009.

[2]李爽.在高中数学中函数思想的应用案例研究[J].数学学习与研究，2013(1).

[3]潘政显.函数思想在高中数学中的应用[J].语数外学习(数学教育)，2013(1).

〔责任编辑：李海波〕

Application of Function and Equation in the High School Mathematics Problem-Solving

LUAN Xiu-ping1, CUI Xian-shun2, PIAO Yong-jie1

(1.College of Science, Yanbian University, Yanji 133002, China;2.Yanbian No.1 Middle School, Yanji 133001, China)

The function and equation have an irreplaceable role in the high school mathematics problem-solving. In view of the concept of function and equation, the paper explores the good mathematical way of thinking so as to improve the quality of student learning and problem- solving rate through the specific analysis of the sequence, the actual problems and the trigonometric function modules in the high school mathematics.

function and equation; high school mathematics; problem-solving application

10.3969/j.issn.1008-6714.2017.03.037

2017-01-07

栾秀平(1991—)，女，吉林延吉人，数学教育专业研究生；通讯作者：朴勇杰(1962—)，男(朝鲜族)，吉林延吉人，教授，理学博士，从事数学教育和非线性分析研究。

G633.6

A

1008-6714(2017)03-0079-02