基于多级维纳滤波的ESPRIT算法
张 超,黎仁刚,顾 军
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
基于多级维纳滤波的ESPRIT算法
张 超,黎仁刚,顾 军
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
因奇异值分解引入了庞大的计算量,子空间分解类的测向算法在工程中难以实现实时处理。多级维纳滤波(MSWF)算法,避免了奇异值分解运算,有效地减少了运算量。通过对多级维纳滤波算法进行改进,提出了一种信源数目的估计方法。与传统多级维纳滤波算法相比,该方法提高了测向精度。通过仿真证明了该算法的有效性。
阵列信号处理;多级维纳滤波;信源数目估计;测向精度
0 引 言
波达方向估计(DOA)在通信、雷达、电子对抗、导航等领域中有着举足轻重的地位[1]。随着信息技术的不断发展,电磁环境变得越来越复杂,传统的测向技术无法满足当下的需求,以MUSIC[2]和ESPRIT[3]算法为代表的超分辨测向算法应运而生,并受到广大研究人员的青睐。但其算法需要进行子空间分解,计算量庞大,不易实现实时性。为了减少算法的运算量,提高测向速度,许多学者也提出了一些方案,文献[4]通过协方差矩阵实值化处理,将复矩阵分解转换成矩阵分解,文献[5]通过将阵元空间转换到波束空间,降低矩阵维度。
以上所提出的算法都需要进行子空间分解,文献[6]提到了传播算子(PA),此方法利用线性算子从阵列数据中提取信号子空间与噪声子空间,以矩阵相乘代替特征值分解,减小了运算量,但此方法无法对信源数目进行估计,需要预先知道信源数目才能构造分块矩阵。Goldstein等人在1998年提出了基于多级维纳滤波的方法[7],此方法在自适应波束形成、自适应干扰抑制等领域广泛应用。文献[8]将多级维纳滤波技术应用在子空间分解类算法中,避免了特征值分解,大大降低了运算量。文献[9]通过协方差矩阵来初始化数据,不需要训练信号就能进行测向,但在低信噪比、小快拍数的情况下,误差变大甚至可能失效。文献[10]通过对初始化数据进行优化,使其在低信噪比、小快拍数的条件下,估计性能得到改善。文献[11]提出了一种信号源数目与波达方向联合估计的方法,但此方法需要进行M(阵元数)次迭代,在阵元数较多的情况下,运算量也较为庞大。本文通过改进多级维纳滤波算法,优化初始矩阵,提出一种高效的信源数目估计方案,在阵元数较多的条件下,与文献[11]中方法相比,有效降低了计算量。
1 改进算法
1.1 信号模型
对于均匀圆阵,N个全向天线均匀分布在圆周上,如图1所示,D个不相关的远场窄带信号入射,方位角与俯仰角分别为θi和βi(i=1,2,…,D)。阵元的输出数据模型为:
X=As+n
(1)
A=[α(θ1,β1),…,α(θD,βD)]
(2)
α(θ,β)=[ej2πcosθsinβ,ej2πcos(θ-φ1)sinβ,…, ej2πcos(θ-φN-1)sinβ]T
(3)
φi=2π(i-1)/N,i=1,2,…,N
(4)
式中:A为均匀圆阵的方向矢量;s为入射信号;n为阵列上的噪声,均值为0,方差为σ2。
噪声相互独立,且与信号互不相关。
对于均匀圆阵而言,其方向矢量的表达式相对较复杂,且不具备均匀线阵的范得蒙矩阵形式。因此,首先要将其进行波束空间转换变成虚拟线阵。
设空间离散傅里叶变换(DFT)矩阵:
(5)
(6)
(7)
(8)
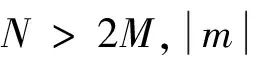
定义变换矩阵C:
C=diag{j-M,…,j-1,j0,j-1,…,j-M}
(9)
FH=VHCWH
(10)
根据X=As+n,求出X的协方差矩阵RX,再将矩阵RX进行变换,得到:
RF=FHRXF
(11)
式中:RF为在波束空间下对应的协方差矩阵,取RF的实部代替RF。
1.2 多级维纳滤波优化
维纳滤波技术是在最小均方误差(MMSE)准则下的一种线性滤波,在已知信号与噪声相关函数的条件下,通过Winner-Holf方程RxWx=r=As+nxd对信号进行最优滤波。Goldstein等人提出的多级维纳滤波技术的思想是通过对观测数据进行多次正交投影,每次投影得到2个子空间,其中一个子空间平行于参考信号与上次观测数据的互相关矢量,另一个子空间正交于这个子空间,然后再对这个正交于互相关矢量的子空间用同样的方法继续进行正交投影。其结构如图1所示。
多级维纳滤波算法需要参考信号di(k)与观测数据Xi(k),而实际工程中,并不一定能够获得,因此采用任意单元的数据来代替参考信号。信号之间相互独立,假设为高斯白噪声。观测信号每次投影,分别得到与观测数据平行的分量和正交的分量,这些代表的就是信号子空间与噪声子空间。具体步骤如下所示:
第1步,初始化观测数据和阵列接收数据:
(12)
(13)
式中:R为协方差矩阵。
第2步,求互相关矢量hi(i=1,2,3,…,D):
(14)
(15)
(16)
(17)
第3步,估计信号源数目,确定信号子空间:
(18)
(19)
式中:S代表信号子空间;G代表噪声子空间。
数据初始化使用协方差矩阵来代替,在文献[10]中提出的初始数据优化方法,通过将协方差矩阵行取平均,得到:
(20)
此方法应用于均匀线阵,在低信噪比、小快拍数条件下,适当提高了算法的估计性能。
本文算法是基于均匀圆阵的,经过波束空间映射到虚拟均匀线阵,模式数为2M+1。本文提出的优化方法是选用协方差矩阵第M行初始化数据:
(21)
针对均匀圆阵,本文所提出的优化方法比起文献[10]中提出的方法,在低信噪比、小快拍数下的精度更高,下文仿真实验可见。
1.3 信号源数目估计
在常规的子空间分解测向算法中,信号源数目的估计一般采用Akaike信息论(AIC)准则和最小描述长度(MDL)准则,这2个准则具有相同的似然函数,只是惩罚函数不一样。但这2个准则的使用前提需要对阵列协方差矩阵进行特征值分解。而在多级维纳滤波算法中,通过正交投影取代了特征值分解。阵列协方差矩阵分解所得到的特征值分别代表信号或噪声功率的大小。与特征值分解类似,通过多级维纳滤波算法得到的正交投影信号d1(k),d2(k),…,dM(k),可以用σi来代表其功率:
(22)
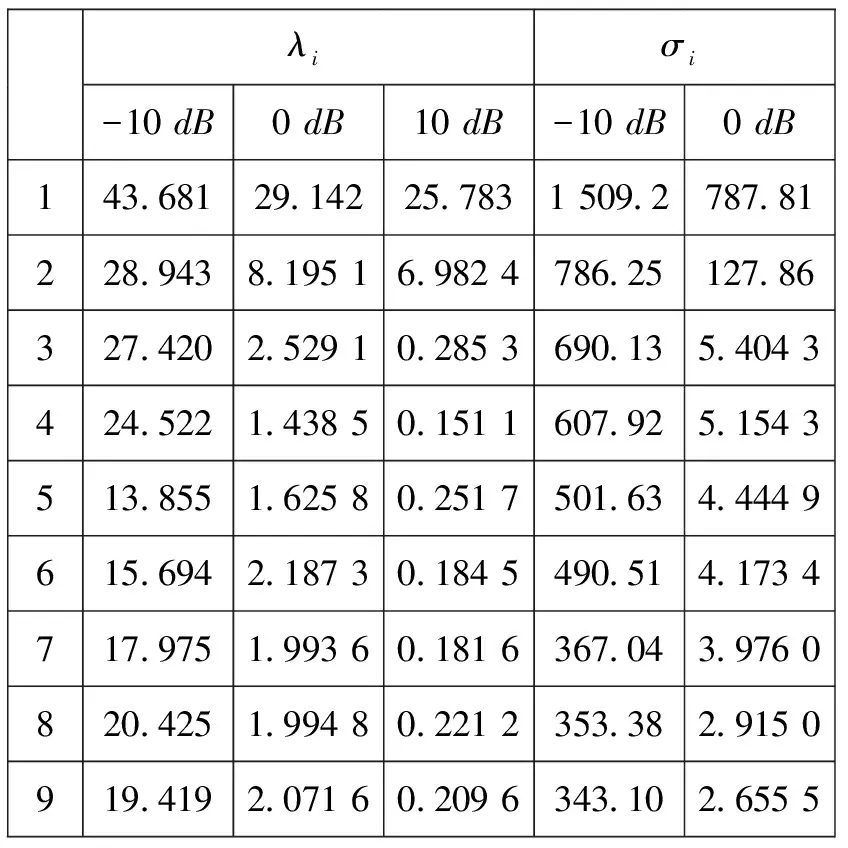
表1 不同信噪比下σi与特征值λi的比较
从表1可以看出,多级维纳滤波算法在低信噪比时,信号能量会泄露到噪声子空间中,导致无法判断信号子空间。文献[7]中提出了一种信号源数目的估计方法,判断信号子空间。但该方法在阵元数比较多的时候,计算量较大。本文提出一种估计方法,适合多阵元数条件下的信号源数目估计。
第1步:初始化后进行4次投影得到正交投影信号,求出代表其功率的σi。
第2步:构造判决函数,判断信号子空间需要滤波的级数:
fori=1:M-4
δi=(σi+1+2σi+2)/3
Δi=(σi-δi)/δi/2
ifΔi<1
ThenD=i
elseifσi<1
ThenD=i
endif
endfor
根据判决,得到信号源数目为i。
第3步:构造信号子空间S=[h1,h2,…,hD]。
1.4ESPRIT算法
经过多级维纳滤波正交投影,得到的信号子空间S=[h1,h2,…,hD]相似于B:
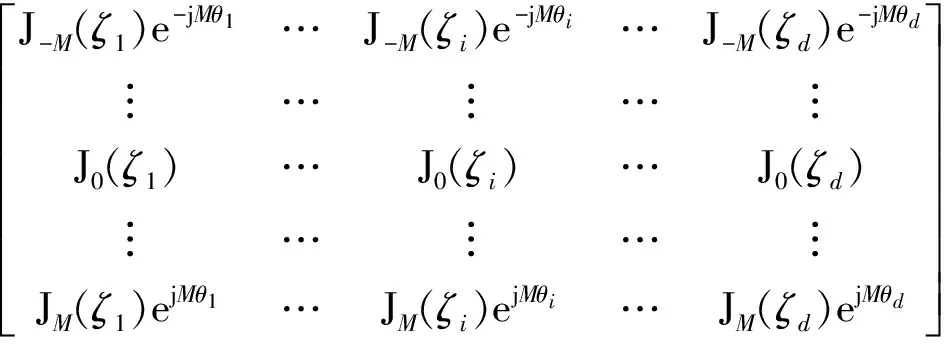
(23)
式中:Jm(ζ)为第一类贝塞尔函数,m为阶数,ζ为变量。
根据贝塞尔函数的性质可得:
ΓZ0=Z-1Φ+Z1Φ*
(24)
Γ=(λ/πr)diag{-(M-1),…,0,…,M-1}
(25)
Φ=diag(sinβ1ejθ1,sinβ2ejθ2,…,sinβDejθD)
(26)
式中:Z-1,Z0和Z1分别为信号子空间Z前2M-1行,中2M-1行和后2M-1行。
最后求解得到Φ,即可估计出信号源方位角与俯仰角。
2 仿真与分析
本文采用阵元数为16的均匀圆阵,模式数2M+1为9,2个不相干的信号源入射角分别为(75°,20°)与(60°,55°),对比常规波束空间ESPRIT算法(算法1)、文献[10]中所提出的算法(算法2)以及本文算法(算法3)3种算法的性能。定义联合均方根误差(RMSE)为:
(27)
式中:P为蒙特卡洛试验次数;θi与βi分别为第i次试验的方位角与俯仰角的估计值;θ与β分别为方位角与俯仰角的真实值。
试验1:选择信噪比为4dB与6dB,在不同的快拍数下,进行200次蒙特卡洛试验,仿真结果如图3所示。
从图3可以看出,小快拍数的情况下,本文算法的估计性能优于常规的多级维纳滤波算法,接近协方差矩阵分解算法的估计性能。随着快拍数的增加,各算法的估计性能也随之提高。
试验2:选择快拍数为40次与80次,在不同的信噪比下,进行200次蒙特卡洛试验,仿真结果如图4所示。
从图4可以看出,在低信噪比的情况下,本文算法的估计性能优于常规的多级维纳滤波算法。随着信噪比的提高,各算法的估计性能也随之提高,并且均方根误差趋于一致。
试验3:对于本文提出的信号源数目估计方法,分别在低信噪比、小快拍数下进行200次蒙特卡洛试验,观察其成功概率。
从图5、图6中可以看出,在低信噪比时随着快拍数增加和信噪比的提高,信号源数目估计的成功概率都将提高。本文提出的信号源数目估计方法中引入了σi<1这一判决条件,可避免在大信噪比时噪声功率偏小,导致噪声功率之间的相对偏差较大,引起估计错误。
传统的多级维纳滤波算法的运算量为O(M3),而本文所提出的信号源数目估计方法的运算量为O[M2(K+3)],其中M为阵元数目,K为信号源数目。相比文献[11]中的信号源数目估计方法,本文方法在阵元数较多而信号源数目较少的情况下,能有效减少运算量。
3 结束语
根据多级维纳滤波的特点,本文提出了一种基于多级维纳滤波的改进算法,用协方差矩阵代替参考信号,并通过优化初始数据来提高估计精度。与常规的子空间分解算法相比,其避免了特征值分解,大大减小了运算量。此外,在多级维纳滤波投影过程中,低信噪比条件下存在子空间泄露问题。本文提出了一种信号源数目的估计方法,能够在低信噪比时有效估计出信号源的数目。尤其是在大阵元数、信号源数目不多的情况下,本文方法比常规多级维纳滤波算法运算量更低,更适用于工程实现。
[1] 王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
[2]SCHMIDTRO.Multipleemitterlocationandsignalparameterestimation[J].IEEETransactionsonAntennasandPropagation,1986,34(3):276-280.
[3]ROYR,PAULRAJA,KAILATHT.ESPRIT——asubspacerotationapprochtoeatimationofParameterofcisoidsinnoise[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing,1986,34(5):1340- 1342.
[4] 孙继红,杨科,张瑾.一种实值MUSIC算法[J].空间电子技术,2006(3):36-38.
[5] 李绍滨,赵宜楠,胡航.均匀圆阵波束空间二维DOA算法[J].哈尔滨工业大学学报,2004,36(6):796- 798.
[6]MARCOSS,BEBIDIRM.Onahighresolutionarrayprocessingmethodnon-basedoneigenanalysisApproach[C]//ETTERDM.InternationalConferenceonAcoustics,speechandSignalProcessing.NewMexico,USA:IEEEPress,1990:2955-2958.
[7]GOLDSTAINJS,REEDIS,ScharfLL.Amultistagerepresentionofthewinnerfilterbasedonorthogonalprojection[J].IEEETransactionsonInformationTheory,1998,44(7):2943-2959.
[8] 黄志忠,李万玉,强勇.多级维纳滤波在子空间类测向算法中的应用[J].火控雷达技术,2009(1):11-14.
[9] 于红旗,黄知涛,周一宇,徐欣.一种不需要特征值分解的ESPRIT方法[J].信号处理,2008(3):357-360.
[10]李堰,宋爱民,刘剑.多级维纳滤波测向算法的参考信号优化方法[J].电讯技术,2010(12):75-80.
[11]包志强,吴顺君,张林让.一种信源个数与波达方向联合估计的新算法[J].电子学报,2006(12):2170- 2174.
ESPRIT Algorithm Baesd on Multi-stage Winner Filtering
ZHANG Chao,LI Ren-gang,GU Jun
(The 723 Institute of CSIC,Yangzhou 225001,China)
Because of the enormous calculating quantity introduced by singular value decomposition,the direction finding algorithm based on subspace decomposition is difficult to be realized in engineering in real time.The multi-stage Wiener filtering (MSWF) algorithm avoids the singular value decomposition calculation,reduces the calculating quantity effectively.This paper puts forward an estimation method of source number by improving MSWF algorithm.The algorithm improves the direction-finding accuracy compared with traditional MSWF algorithms.The validity of this algorithm is validated through simulation.
array signal processing;multi-stage Wiener filtering;estimation of source number;direction-finding accuracy
2016-09-01
TN971.1
A
CN32-1413(2017)01-0074-05
10.16426/j.cnki.jcdzdk.2017.01.016

