改进型PID控制永磁偏置磁悬浮轴承

谢 磊，聂洪平,何 莹

(1.中国海上卫星测控部，江阴 214431;2.泰州学院，泰州225300)

改进型PID控制永磁偏置磁悬浮轴承

谢 磊1，聂洪平1,何 莹2

(1.中国海上卫星测控部，江阴 214431;2.泰州学院，泰州225300)

针对传统PID控制超调与调节时间存在矛盾及磁悬浮轴承的特殊性，提出了具有一定非线性补偿能力的改进型PID控制算法，根据偏差与偏差变化率的关系，使比例、积分、微分调整大小、分时作用。在MATLAB的Simulink环境下搭建永磁偏置磁悬浮轴承的控制系统模型，用 S-function函数实现改进型PID的控制算法和永磁偏置磁悬浮轴承的非线性模型，并进行了动态仿真。仿真结果表明，改进型PID控制器相对于传统PID控制器对永磁偏置磁悬浮轴承在动态性能、抗干扰能力上有比较好的控制效果，且提高了永磁偏置磁悬浮轴承的刚度，其算法在数字控制器中较容易实现。

永磁偏置磁悬浮轴承；控制系统；非线性；改进型PID

0 引 言

磁悬浮轴承通过控制磁力的大小与方向使转子稳定悬浮，具有摩擦损耗小、不需润滑、使用寿命长、对极端高温、极端低温适应性好等优点，在高速驱动、多电全电飞机等领域具有广泛的应用前景[1-2]。磁悬浮轴承本质是一个二阶不稳定系统，必须通过闭环控制才能实现转子的稳定悬浮[3]。磁悬浮轴承的性能很大程度上取决于控制系统，其刚度和阻尼都与控制系统有关。对于磁悬浮轴承系统，目前PID控制仍然比较普遍，传统的PID控制器结构简单，易于实现，其稳定性好，但传统PID控制中超调与调节时间之间存在矛盾，控制的稳定性与轴承的刚度之间存在矛盾[4-5]。文献[6]提出的变速积分PID控制在磁悬浮轴承中的应用与改进对积分控制提出了改进，但使系统稳定的基本控制规律是PID控制，该文献未对比例与微分环节提出改进方案；文献[7-9]提出的变参数PID控制，根据偏差大小与偏差变化量(非负)取比例、积分、微分参数，但在不同区域所取参数的大小有一定的盲目性，有时难以调到合适的参数，且没有体现参数与偏差的动态关系；文献[10]体现了PID参数与偏差的动态关系，但没有考虑到磁悬浮轴承起浮阶段偏差较大且偏差往减小方向变化的特殊性，其所搭建的控制对象模型是基于磁悬浮轴承在平衡位置附近的线性化模型，没有充分考虑到磁悬浮轴承在远离平衡位置处的非线性特性，没有考虑到在偏差较大时比例系数较大，完全取消微分作用容易产生较大超调，其算法应用于本实验室永磁偏置磁悬浮轴承产生较大超调。针对以上算法的不足，本文在基于有限元仿真的前提下考虑软磁材料的磁阻及漏磁阻，建立较为准确的永磁偏置磁悬浮轴承的磁路模型，在MATLAB的Simulink环境下通过S-function函数实现永磁偏置磁悬浮轴承的非线性模型，在考虑起浮阶段特殊性的前提下，改进型PID根据偏差和偏差的微分关系使比例、积分、微分分时作用，改善系统性能，提高磁悬浮轴承的刚度。

1 永磁偏置磁悬浮轴承工作原理及数学模型

以三自由度永磁偏置磁悬浮轴承为例，其磁通路径如图1 所示[11-13]。

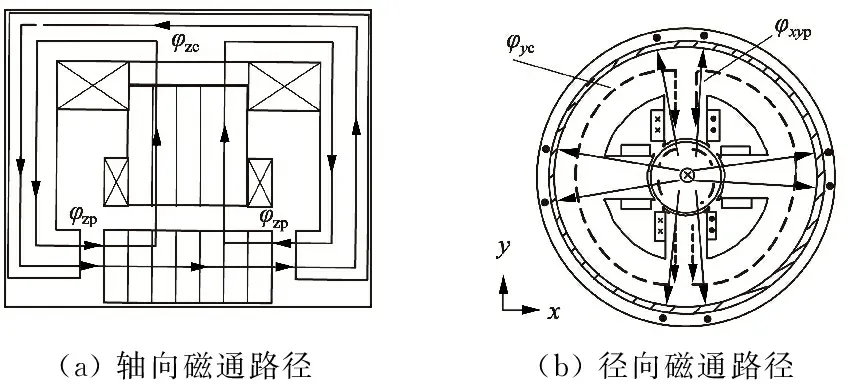
(a)轴向磁通路径(b)径向磁通路径

图1 磁通路径

永磁偏置磁悬浮轴承一般采用差动激磁方式，当转子受到扰动偏离平衡位置时，位移传感器检测出磁悬浮轴承转子位置信号传递给处理器，处理器输出控制信号经功率放大电路转化为控制电流，产生电磁场，转子气隙增大侧的磁场是永磁铁产生的磁场与电磁铁产生的磁场相加，转子气隙减小侧的磁场是永磁铁产生的磁场与电磁铁产生的磁场相减。通过改变控制电流的大小和方向，改变转子所受合力，使转子稳定在平衡位置。

针对磁悬浮轴承的受力分析通常采用等效磁路法，为简化磁路模型，一般不考虑软磁材料磁阻与漏磁阻，这样建立的磁路模型不精确，计算结果存在较大偏差。文献[14]在充分考虑上述两者的前提下，建立永磁偏置三自由度磁悬浮轴承等效磁路模型，并对各部分磁阻进行量化分析。本文根据其研究成果，计及气隙及永磁体处漏磁，依据有限元仿真结果建立永磁偏置磁悬浮轴承等效磁路模型，如图2、图3所示。

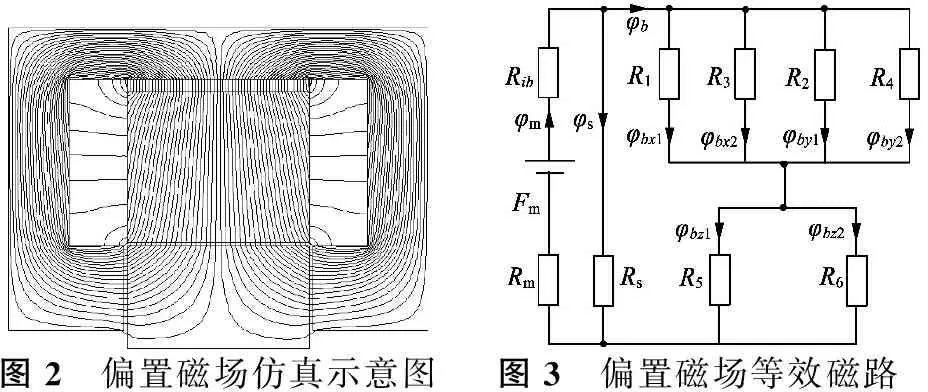
图2 偏置磁场仿真示意图图3 偏置磁场等效磁路

图3中，Fm为环形永磁体磁动势，Rm为永磁体磁阻，Rs为漏磁阻，包括永磁体漏磁与气隙处漏磁。径向气隙磁阻R1,R2,R3,R4以及轴向气隙磁阻R5,R6分别并联连接，以轴向永磁偏置磁悬浮轴承为例，磁拉力：

偏置磁通：

Rs1,Rs2分别为永磁体漏磁和气隙处漏磁,参考文献[19]中磁悬浮轴承设计方法,漏磁阻计算式:

轴向控制磁场仿真及等效磁路图如图4、图5所示。

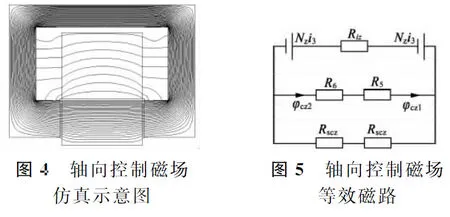
Rsz=1∫Do2Di28μ0r(2r-Drpi)dr(6)

φcz=2NrirR5+R6(7)

将式(1)在x=0,ir=0处泰勒展开，忽略二阶以上无穷小量,得

式中:kx为永磁偏置磁悬浮轴承的位移刚度，kiz为永磁偏置磁悬浮轴承的电流刚度。对于一个确定的永磁偏置磁悬浮轴承系统，在平衡位置附近，二者的大小是确定的。

式(8)即为在小偏差范围内得到的永磁偏置磁悬浮轴承推力线性化模型。由式(1)～式(7)可以看出，永磁偏置磁悬浮轴承系统的磁拉力与转子位置、绕组电流、磁悬浮轴承结构参数是复杂的非线性关系。

2 改进型PID 控制器

传统的PID控制器如图6所示。

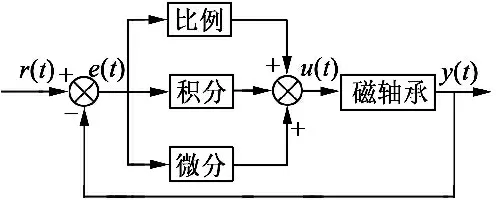
图6 标准PID控制系统

标准的PID控制系统包括PID控制器和被控对象永磁偏置磁悬浮轴承两部分，永磁偏置磁悬浮轴承转子与平衡位置的位移偏差作为控制器的输入，控制器根据控制算法算得控制永磁偏置磁悬浮轴承所需的电流控制被控对象。其控制规律

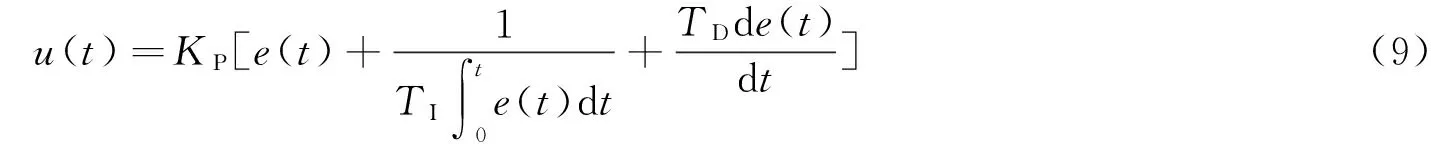
式中:KP为比例系数；TI为积分时间常数；TD为微分时间常数。

比例环节是成比例地反映永磁偏置磁悬浮轴承与平衡位置之间的位移偏差，位移偏差一旦产生，比例控制器瞬间对其作出反应，使磁悬浮轴承向平衡位置运动。增大比例系数，磁悬浮轴承向平衡位置运动的速度变快；反之，减小比例系数，运动速度变慢，增加系统的调节时间。但在平衡位置附近，如果比例系数选择过大，则会导致磁悬浮轴承的运动速度过快，产生较大超调，甚至可能使系统不稳定。对于永磁偏置磁悬浮轴承系统而言，比例系数还与永磁偏置磁悬浮轴承刚度相关。刚度是轴承的基本参数之一，刚度过高，磁悬浮轴承在小位移偏差时就会产生很大的力，有可能使系统达到力饱和。刚度过低，若系统刚度与轴承负刚度kx不在一个数量级上，kx的精度偏差可能使系统不稳定。一般选取合适的比例系数，使系统刚度为轴承负刚度的2～8倍。

微分环节影响磁悬浮轴承位移偏差的变化趋势，当磁悬浮轴承向某个方向运动时，提前预报磁轴承位移偏差的变化方向，有效减小超调[15]。微分系数(kD=kPTD)影响磁悬浮轴承控制系统的阻尼比，阻尼比过小，起浮阶段和受干扰时振荡加剧，系统相对稳定性变差。增加阻尼意味着增加微分系数，阻尼过大，将导致系统调节时间过长，且微分作用会放大反馈信号中的干扰，因此不能过大，一般选取合适的微分系数，使阻尼比为0.5～1。

积分环节将磁悬浮轴承控制系统位移偏差的累积作为输出，主要用于消除系统静差，提高系统无差度[15]。积分系数(kI=kP/TI)越大，系统静差越小，但同时系统动态响应变慢，在位移偏差较大时易引起积分饱和。

PID控制器基于磁轴承位移偏差信号的比例、积分、微分运算的简单线性组合控制磁轴承，系统的快速性与鲁棒性存在严重的矛盾。控制器的参数基于永磁偏置磁悬浮轴承在平衡点附近线性化后设计，在远离平衡位置处，控制参数可能不匹配。对于永磁偏置磁悬浮轴承这种非线性、时变、强耦合系统而言，传统PID控制效果往往不是很理想。

本文提出的改进型PID控制算法，以磁悬浮轴承位移偏差与位移偏差变化率作为改进型PID控制器的输入，根据位移偏差的大小与变化率在系统响应的过程中动态调整控制器的参数。

3 改进型PID控制算法

3.1 改进型比例控制

当系统出现干扰，磁悬浮轴承转子位移偏差变化率必然发生较大变化。当偏差与偏差变化率乘积大于0(或偏差较大，针对起浮阶段)，表明磁悬浮轴承正向远离平衡位置方向运动，此时补偿环节应适当放大比例系数，及时消除扰动对磁悬浮轴承的影响。当偏差与偏差变化率乘积小于0且偏差较小，表明磁悬浮轴承正向平衡位置运动，此时应使调节器的输出小于补偿前调节器的输出，尽量避免过调造成振荡，缩小调节时间，增强鲁棒性。具体实现形式如图7所示。

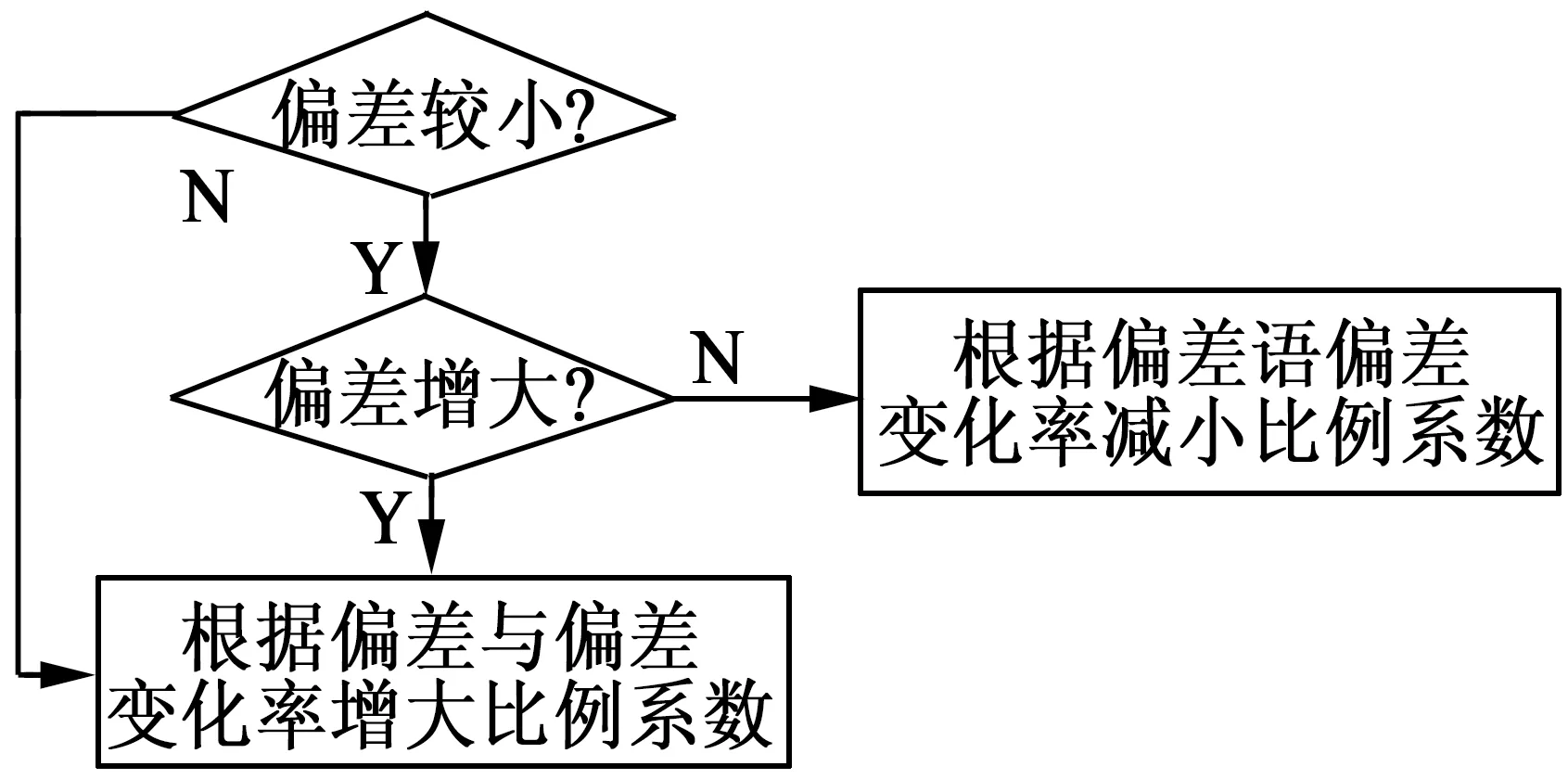
图7 比例系数调整准则

3.2 改进型积分控制

假设磁悬浮轴承控制系统位移偏差曲线如图8所示，在(a，b)与(b，c)中，系统出现超调，常规控制是增加负量控制，以压低超调，但由于(o，a)区间存在位移偏差累积，(a，b)与(b，c)积分首先要抵消(o，a)区间作用，延长系统过渡时间；在(c，d)与(d，e)中，积分作用使磁悬浮轴承向平衡位置运动。但在(d，e)区间积分作用继续增强，结果势必造成磁悬浮轴承控制系统再次出现超调。

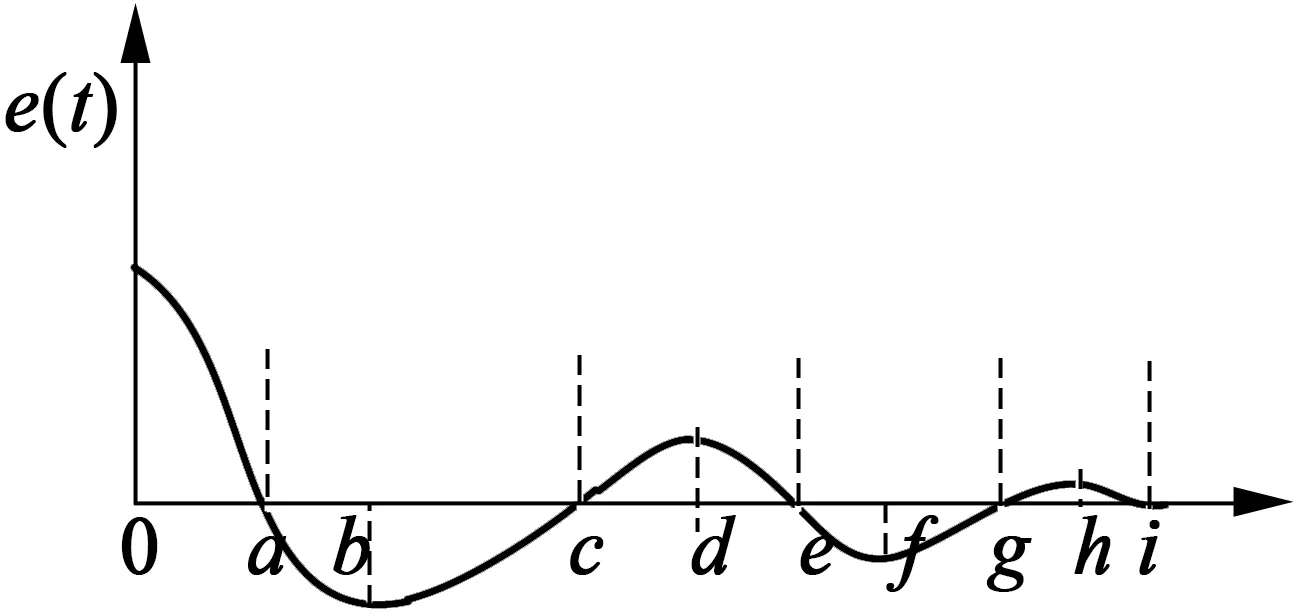
图8 偏差曲线

基于以上积分控制控制磁悬浮轴承的缺点，改进型积分控制仅在(a，b),(c，d),(e，f),(g，h)区间积分，抑制磁悬浮轴承系统的稳态偏差；在磁轴承向平衡位置运动时取消积分作用，系统靠惯性向平衡位置运动，但此时系统比例微分仍起作用。这种积分有选择的记忆有用信息，遗忘无用信息，能克服常规积分作用的一些缺点。

3.3 改进型微分控制

微分系数主要是响应磁悬浮轴承位移偏差变化速率的，当位移偏差导数较大时，微分作用在一定程度上会抵消比例控制的作用，使轴承到达平衡位置的时间延长。因此，在磁轴承起浮阶段微分控制作用不能太强，但也不能为0(或者太小)，因为此时比例系数较大，微分太弱，极易出现大的超调；当偏差接近0时，则加强其作用。

综上所述，在磁悬浮轴承位移偏差较大时根据偏差与偏差变化率增大比例系数，同时取较小微分系数；偏差较小时，取较大微分系数，同时判断偏差变化方向：若偏差往减小方向变化，则根据偏差与偏差变化率减小比例系数，取消积分作用；若偏差往增大方向变化，则根据偏差与偏差变化率增大比例系数，加入积分作用。

4 系统仿真研究

在MATLAB的Simulink环境下搭建如图9所示系统，模拟实际系统从左到右分别为控制器、功放电路、单相全桥电路、控制对象永磁偏置磁悬浮轴承。通过S-function函数编程实现改进型PID控制模块与永磁偏置磁悬浮轴承非线性模型，比例系数具体实现形式如下[16]：

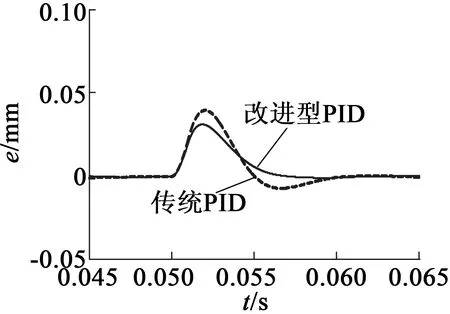
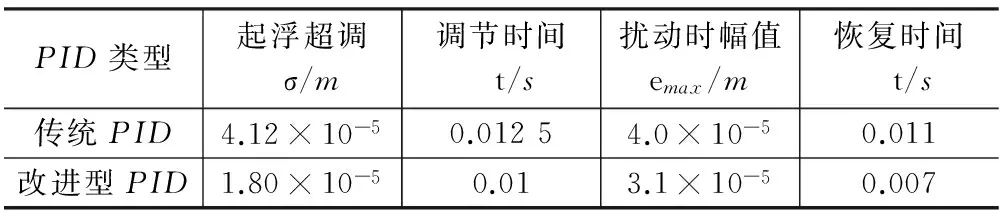
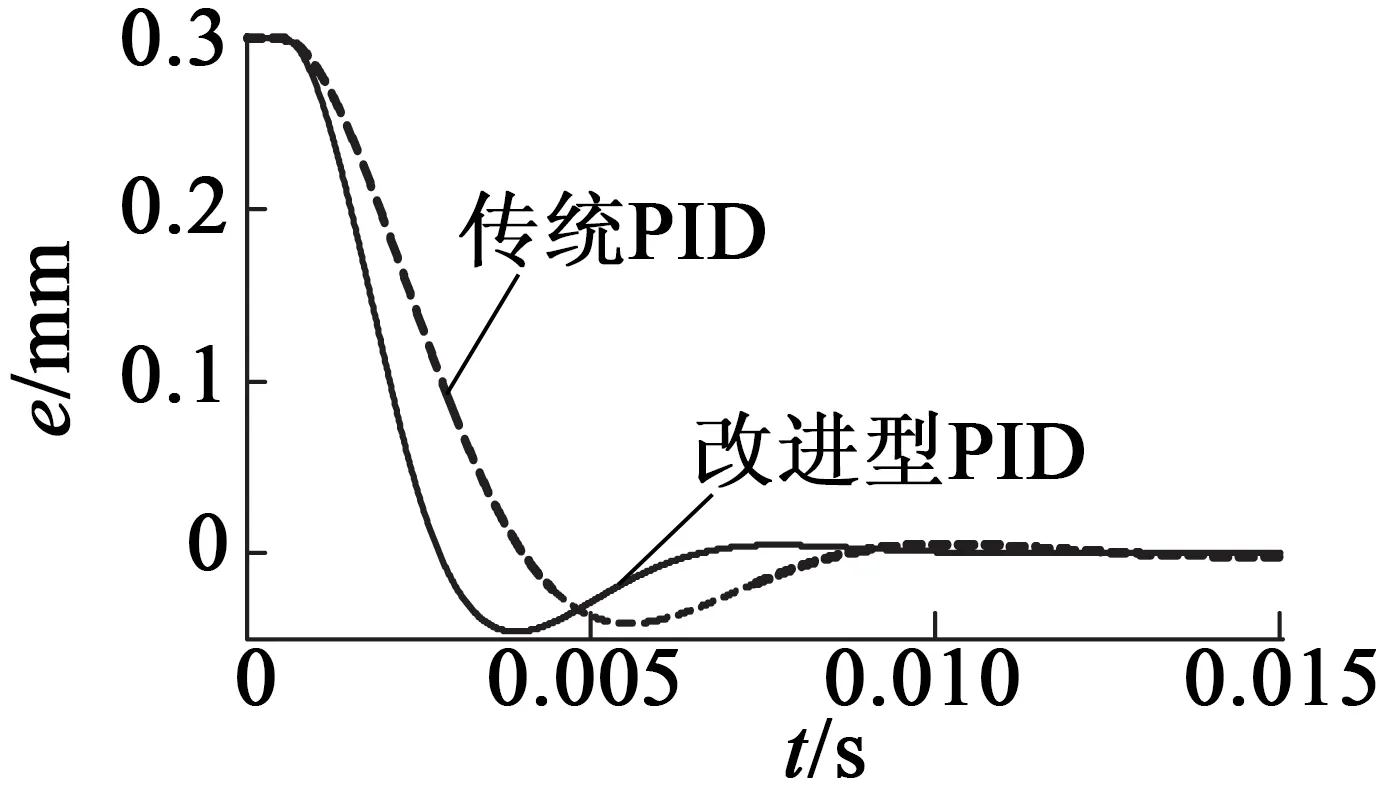
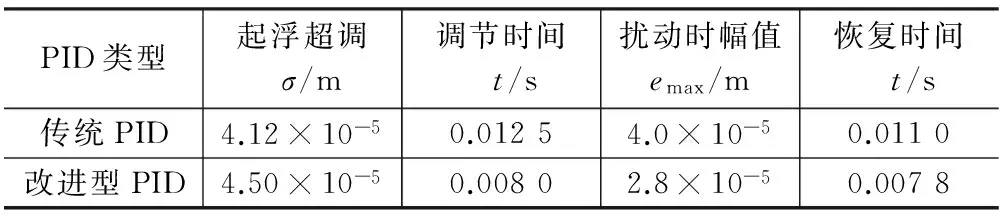
if((e>0 &&e>e1)||e>0.5)|| ((e<0 &&e

kpn=6.15*(1+k0*(1-exp(abs(k1*(e-e1)))));

elseif(e>0 &&ee1 &&e>-0.5)

kpn=kp*exp(-abs(k2*(e-e1)));

其中e为本次采样误差；e1为上一次采样误差；k0,k1,k2是放大系数；kp是补偿前的比例增益；kpn是补偿后的比例增益，控制系统框图如图9所示。

图9 控制系统框图

仿真数据取自实际永磁偏置磁悬浮轴承实验装置，气隙宽度为0.5mm，位移刚度为4 880N/mm，电流刚度为628N/A，质量为3.5kg，根据参数整定原则与仿真取比例系数为5，积分系数为3，微分系数为0.002，放大系数k0为3.5，k1为2.5，k2为0.05。系统在0.05s时施加200N的干扰，持续时间为0.001s。观察控制系统对永磁偏置磁悬浮轴承起浮与受扰动时的控制效果。

起浮阶段与扰动时仿真结果如图10、图11所示；而控制性能比较结果如表1所示。

图10 永磁偏置磁悬浮轴承起浮仿真

图11 永磁偏置磁悬浮轴承扰动仿真

表1 传统PID与改进型PID控制性能比较

由图10及表1可见，改进型PID控制永磁偏置磁悬浮轴承超调很小，可以进一步增加比例系数，减小调节时间，增加磁悬浮轴承刚度。增加比例系数到6，其余参数不变，仿真结果如图12、图13所示，在保证起浮超调大致相同的情况下，减小了调节时间，且抗干扰能力变得更好。表2为传统PID与改进型PID(加刚度)控制性能比较结果。

图12 永磁偏置磁悬浮轴承起浮仿真

图13 永磁偏置磁悬浮轴承扰动仿真

表2 传统PID与改进型PID(加刚度)控制性能比较

仿真结果表明，改进型PID控制要比传统PID控制输出超调量小很多,进一步提高比例系数，减小调节时间，提高了磁悬浮轴承的刚度和抗干扰能力,说明其控制特性要优于传统PID控制。

5 结 语

根据传统PID控制的一些缺点以及磁悬浮系统的特殊性，提出了一种改进型PID控制永磁偏置磁悬浮轴承的控制算法，根据系统偏差与系统偏差变化率，对PID控制进行一定程度的非线性补偿，新控制器的动、静态性能得到改善，有更强的鲁棒性，提高了永磁偏置磁悬浮轴承的刚度。另外，数字控制器很容易实现这些控制思想或算法。

[1] SCHWEITER G,BLEULER H,TRAXLER A.Active magnetic bearings basics, properties and application of active magnetic bearings[M].ETH：Switzerland,1994.

[2] 虞烈．可控磁悬浮转子系统[M]．北京：科学出版社，2003．

[3] 苏义鑫，王娟，周祖德，等．主动磁轴承的MATLAB仿真研究[J]．武汉化工学院学报，2003，25(2)：51-53．

[4] 王晓琳，贺鹏．无轴承扰动补偿悬浮系统的稳定性分析与验证[J].控制理论与应用，2012，29(5)：665-672．

[5] 王晓琳，丁强．基于速度信息观测的无轴承永磁同步电机悬浮解耦控制[J].控制理论与应用，2011，28(12)：1803-1807．

[6] 丁懿，郝娟，肖定国，等．变速积分PID控制在磁悬浮轴承控制中的应用和改进[J].实验室研究与探索，2006，25(3)：287-289．

[7] 钟庆昌，谢剑英，李辉.变参数PID控制器[J].信息与控制，1999，28(4)：273-277．

[8] 朱建公，张俊俊.变参数PID控制器设计[J].西北大学学报，2003，33(4)：397-400．

[9] 苏义鑫，王娟，胡业发. 磁悬浮轴承的变参数PID 控制[J].武汉理工大学学报(信息与管理工程版)，2004，26(2)：35-37.

[10] 梁立超，蒋启龙，王麦海,等．磁轴承轴向控制系统的仿人智能PID控制[J].机械工程与自动化,2006，6(3)：116-118.

[11] 汪波．高速磁悬浮开关磁阻电机的研究[D]．南京：南京航空航天大学，2012．

[12] 赵旭升，邓智泉，王晓琳，等．永磁偏置轴承的研究现状及其发展[J]．电工技术学报，2009，24(9)：9-20．

[13] 李冰，邓智泉，严仰光．一种新颖的永磁偏置三自由度电磁轴承[J]．南京航空航天大学学报，2003，35(1)：81-85.

[14] PICHOT M A,KAJS J P,MURPHY B R.Active magnetic bearings for energy storage systems for combat vehicles[J].IEEE Transactions on Magentic,2001,37(1):318-323．

[15] 陶永华，尹怡欣，葛芦生.新型PID控制及其应用[M].北京：机械工业出版社，1998.

[16] 李祥生，邓智泉，陈志达，等．一种电流型四桥臂开关功放控制方法的研究[J]．电工技术学报，2011，26(2)：156-164.

Improved PID Control of Permanent Magnet Bias Magnetic Bearings

XIELei1，NIEHong-ping1，HEYing2

(1.China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China；2.Taizhou University,Taizhou,225300,China)

For contradictions of conventional PID control overshoot and settling time and magnetic bearings are unique, made with a certain nonlinear ability to compensate improved PID control algorithm, according to the deviation and the deviation rate of change of its relationship with the proportional, integral, differential resize , time effect. In the MATLAB Simulink environment to build control system model, using S-function function to prepare the modified PID control algorithm and permanent magnet bias magnetic bearings nonlinear model and the dynamic simulation. Simulation results show that the improved PID controller relative to the conventional PID controller for permanent magnet bias magnetic bearings in a dynamic performance, anti-jamming capability has better control effect and improves the stiffness of permanent magnet bias magnetic bearings, which algorithm more easily achieved in the digital controller.

permanent magnet biased magnetic bearings； control systems； nonlinear; improved PID

2016-04-05

TH133.3;TM315

A

1004-7018(2017)02-0023-04

谢磊,男，硕士研究生，研究方向为伺服控制。