基于组结构字典稀疏表示的地震数据随机噪声压制

徐小红, 张 洋, 屈光中, 毕云云

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

基于组结构字典稀疏表示的地震数据随机噪声压制

徐小红, 张 洋, 屈光中, 毕云云

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

基于地震数据自身学习得到的自适应字典能够更精确地表示地震数据,针对稀疏表示传统方法训练出来的自适应字典的无结构性问题,文章提出一种基于组结构字典稀疏表示的地震数据随机噪声压制算法。该算法首先通过地震数据本身训练得到自适应学习型并具有一定结构性的组结构字典,然后利用该组结构字典对地震数据进行稀疏表示,通过得到的表示系数重建地震数据。所用的组结构字典能够更好地适应地震数据自身特性,对地震数据进行稀疏表示可得到更加稀疏的表示系数,滤除了通常系数很小的随机噪声,从而能够有效压制随机噪声。实验表明,文中所提出的地震数据随机噪声压制算法具有良好的去噪效果。

稀疏表示;字典学习;组结构字典;地震数据去噪

0 引 言

地震资料中常常含有较强能量的随机噪声,如微震、背景干扰等,这些噪声的存在极大地降低了地震资料的信噪比,严重影响地震资料的后续处理流程,降低地震记录的解释精度,因此地震数据噪声的压制显得尤为关键。为有效去除地震数据中的随机噪声,国内外研究者提出了多种去除随机噪声的方法。按去噪机制的不同可归为3类。

第1类,基于滤波的去噪方法,该类方法利用有效信号和噪声在空间域、频率域或频率波数域内具有较好的分选性,通过滤波的方式对噪声进行去除,其中较常用的有中值滤波[1]、F-K滤波[2]、F-X反褶积滤波[3]等。

第2类,基于变换的去噪方法,该类方法利用有效信号和噪声经某种变换后投影到变换域内系数具有可分离性来对两者进行分离,主要有傅里叶变换法[4]、离散余弦变换法[5]、小波变换法[6-7]、曲波变换法[8]等。

第3类,基于有效信号相干性的方法,该类方法通过利用多道地震信号的相干性以及噪声的随机性,提取有效信号特征值重构信号,实现噪声的去除,常用的方法有多项式拟合去噪以及奇异值分解(singular value decomposition，SVD)去噪[9]等。

基于变换的去噪方法是在随机噪声的压制中比较常用的方法。其中,傅里叶变换由于不具备时频局部性,不能有效捕捉到地震数据的局部特征;小波变换虽然能够更好地捕捉信号的局部性特征,但是不具备方向识别能力,只对点奇异特征有很好的捕捉性能,而地震数据通常是由地震波前构成的曲线奇异,因此,小波变换也不是处理地震数据的理想变换;曲波变换具有多尺度和方向选择性,更适合表示具有较多曲线特征的地震数据,然而曲波变换会产生伪影现象,同时在同相轴边缘产生不光滑现象,影响地震数据去噪质量。该类方法都是事先选定某一固定变换基,不能根据数据特征的变化而变化,从而不能有效表示地震数据,影响去噪效果。

自适应学习基可通过数据本身训练学习得到,能根据数据本身的特点自适应地调整基函数,能够更好地表示地震数据。基于稀疏表示的随机噪声去除方法既可利用固定变换字典表示数据,也可通过字典学习得到自适应字典,提高数据表示的精度。文献[10]提出一种基于自适应学习型字典表示的地震数据随机噪声压制方法,该方法通过地震数据本身学习训练自适应字典对地震数据进行稀疏表示,得到稀疏的表示系数,再通过稀疏表示系数重建信号。在稀疏编码阶段,在求得的稀疏的地震数据表示系数中,表示随机噪声的小系数被剔除了,因此，用稀疏的表示系数重建地震数据时,数据中的随机噪声能够被有效地去除,取得了良好的去噪效果。

基于稀疏表示的地震数据噪声压制要达到理想的去噪效果,需所用字典能用较少的原子或基函数逼近原始地震信号,即要求所用的字典能有效地表示地震数据。结构稀疏性[11-12]可考虑信号的空间结构性,将这种结构稀疏性约束于字典学习中,相比于稀疏表示中传统的字典学习得到的字典的无结构性,则能够更加稀疏地表示信号。因此,本文结合自适应学习型字典和组结构稀疏性[13-17],基于地震数据本身,训练出一种能够充分表示地震数据自身特性的自适应学习型结构性字典,利用该字典对地震数据进行稀疏重建,提高了地震数据的信噪比。

1 地震数据稀疏表示去噪模型

1.1 基于稀疏表示的地震数据去噪

含噪地震数据模型可表示为:

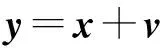
(1)

其中,x为待估计的不含噪声地震数据,常被噪声污染;v为非耦合的随机噪声;y为所测得的含噪地震数据。

所谓噪声压制,是指从测得的含噪数据y中估计出x,即通过一定的方法来降低噪声v。地震信号x在某一变换字典D下的稀疏表示模型为:

(2)

其中,α为x在变换域D中的表示系数向量。α的0-范数‖α‖0表示α中非零元素的个数,其值越小,表示α越稀疏,同时也意味着信号x在该变换域内越稀疏。

基于稀疏表示的地震数据去噪问题可以描述为如下一般的形式[18]:

(3)

其中,D为选定的某种变换字典;λ为正则参数。

1.2 学习型字典表示下的地震数据去噪

设有n个含噪地震数据训练样本yi∈Rm(i=1,2,…,n),假设每个样本yi都可以表示为字典D中部分原子的线性组合,即可通过字典学习方法训练字典,得到基于地震数据自身特性的自适应学习型字典。

自适应字典的学习过程可描述为下述问题的优化过程:

(4)

其中,D为期望学习得到的字典;αi为yi在字典D下的分解系数向量;λ为正则参数,用来平衡信号的重建误差精度和稀疏度。

(4)式的第1项是重建能力约束项,第2项是稀疏度约束项。K奇异值分解(K-singular value decomposition，K-SVD)[19]、最优化方向(method of directions，MOD)[20]等都是比较经典的字典学习方法。

将地震数据的字典学习过程和信号重建过程结合,基于学习型字典稀疏表示的地震数据去噪可以通过最小化如下函数来求解[18]:

(5)

2 组结构字典表示下的地震数据去噪

2.1 组结构字典学习

传统的字典学习算法只考虑了表示系数向量的整体稀疏性,并没有考虑到稀疏表示向量中任何隐藏的结构,因此学习得到的字典没有结构性。组结构稀疏旨在对稀疏表示向量进行分组,分别考虑每个组的稀疏性,用来反映稀疏表示向量中的相邻元素间的局部依赖性,通过更新字典的过程,将这种结构反映到字典中。

利用稀疏表示系数组结构稀疏性来学习得到的结构性字典称为组结构字典(group-structured dictionary，GSD)。设集合{1,2,…,p}被划分成s个不相交的组G1,G2,…,Gs,若给定n个维度为m的地震数据训练样本yi∈Rm(i=1,2,…,n),则组结构字典的学习过程可描述为下述问题的优化过程:

(6)

其中,DG∈Rm×p为想要学习得到的组结构字典;αi为yi在字典DG下的分解系数;αiGj为αi的索引在组合Gj内的系数。(6)式第1项为重建能力约束项;第2项为稀疏系数向量分组及每组稀疏性的正则约束项,其既保证稀疏表示系数向量稀疏性又考虑了表示系数向量相邻元素间的局部依赖性,使得学习得到的字典具有结构性。

块坐标下降算法(block-coordinate descent,BCD)[21-23]是目前广泛采用的字典学习算法,其思想是固定其中一个变量,优化关于另一个变量的问题,如此2个变量交替迭代直到收敛。

(6)式组结构字典学习即可用该算法来学习,学习过程可分为2个阶段。

第1阶段，利用DG,t-1(假设当前是第t次迭代)求未知的表示系数；由于DG,t-1、yi已知，则可通过求解(7)式最小化任务得到未知的αi,t，即

(7)

第2阶段，由得到的αi,t求解(8)式，得到组结构字典DG,t。

(8)

通过上述2个不断交替的过程，最终可以得到自适应学习型的具有结构性的组结构字典DG。

2.2 基于组结构字典的地震数据去噪

本文将上述具有结构性的组结构字典应用于地震数据稀疏表示中，并提出一种基于组结构字典表示的地震数据随机噪声压制算法。给定n个含噪地震数据训练样本yi∈Rm(i=1,2,…,n)，则地震数据基于组结构字典的去噪可通过求解如下函数最小化问题来实现：

(9)

基于组结构字典稀疏表示的地震数据随机噪声压制算法流程如下。

输入：初始含噪地震数据y。

(1) 初始化。初始信号x=y，初始字典D=D0。

(2) 组结构字典学习(迭代J次)。利用BCD算法进行字典学习，学习过程分为稀疏编码和字典更新2个不断更替的阶段，直到迭代结束。

3 实验结果与分析

3.1 合成地震数据处理

实验在Matlab环境下运行,所用数据是合成的标准segy格式地震数据,含有601道,每道包含2 000个采样点。含噪地震数据是通过添加加性随机噪声得到的。利用信噪比来衡量各类字典的去噪效果。定义信噪比为:

(10)

为测试本文算法的性能,选取离散余弦变换(discrete cosine transform，DCT)字典和无结构学习型字典(K-SVD,由地震数据本身通过K-SVD算法训练得到)对地震数据进行稀疏表示重建,与本文具有组结构的学习型字典(GSD,由地震数据本身训练得到)进行对比实验。

实验结果见表1所列,从表1可以看出,单一固定字典(DCT字典)的去噪效果要比基于数据本身学习得到的字典(学习型字典、学习型组结构字典)的去噪效果差;而具有一定结构性的组结构字典比无结构学习型字典的去噪效果更好。

表1 不同字典去噪后的信噪比 dB

各个字典稀疏表示下的去噪结果如图1所示。本文算法去噪下第1道地震数据的去噪结果如图2所示,从第1道数据的去噪分析中可以清晰地看出本文算法能够有效去除随机噪声。

上述地震数据去噪实验通过纵向对比基于不同字典稀疏表示的地震数据去噪,有效证明了本文去噪算法的优越性。

F-X域反褶积滤波算法因其简单高效而被普遍应用于地震数据随机噪声的压制中;曲波变换(curvelet transform，CT)在地震数据稀疏表示中有着广泛的应用,其能够有效进行地震数据去噪处理。下面通过实验来横向对比本文算法与以上2种方法的去噪效果,实验结果见表2所列,从表2可以看出本文算法与上述2种去噪方法相比,有着更优的去噪效果,充分证明了本文去噪算法的有效性。

图1 不同字典的去噪结果

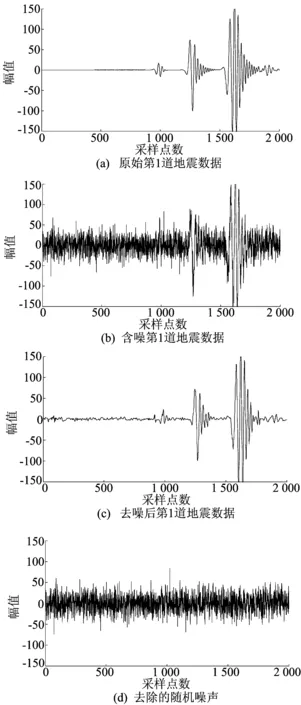
图2 本文算法第1道合成地震数据去噪结果 表2 不同方法去噪后的信噪比

dB

3.2 实际地震数据处理

本文算法在实际地震数据处理中的有效性如图3所示。

实际地震数据剖面如图3a所示,共240道,每道720个采样点,可看出在实际地震数据中含有较多无规则的随机噪声,严重干扰有效信息的解释。使用本文算法对图3a数据进行降噪,噪声得到压制,有效信息突显出来。

图3 实际地震数据去噪结果

4 结 论

基于稀疏表示的地震数据去噪的关键点是寻找到能够有效表示地震数据的稀疏变换字典。本文结合稀疏表示信号中的组结构稀疏性,通过组结构字典学习算法训练出具有一定结构性的字典,其不仅能够根据地震数据自身的变化而变化,而且能够反映信号的结构信息,有效提高了表示数据的精度。本文利用该组结构字典,提出基于组结构字典稀疏表示的地震数据随机噪声压制算法。实验结果表明,本文所提出的去噪算法具有更好的去噪效果。

[1] LIU Y，LIU C，WANG D.A 1D time-varying median filter for seismic random，spike-like noise elimination[J].Geophysics，2009，74(1)：V17-V24.

[2] NAGHIZADEH M.Seismic data interpolation and denoising in the frequency-wavenumber domain[J].Geophysics，2012，77(2)：V71-V80.

[3] CHEN Y，MA J.Random noise attenuation by f-x empirical-mode decomposition predictive filtering[J].Geophysics，2014，79(3)：V81-V91.

[4] CANALES L L.Random noise reduction[C]//54th Annual International Meeting of Society of Exploration Geophysicists.[S.l.:s.n.]，1984：525-572.

[5] 陆文凯.基于离散余弦变换的地震随机噪声压制技术[J].石油地球物理勘探，2011，46(2)：202-206.

[6] 文莉，刘正士,葛运建.小波去噪的几种方法[J].合肥工业大学学报(自然科学版)，2002，25(2)：167-172.

[7] WANG G X，CHEN L，GUO S，et al.Application of a new wavelet threshold method in unconventional oil and gas reservoir seismic data denoising[J].Mathematical Problems in Engineering，2015(3)：1-7.

[8] GO′RSZCZYK A，ADAMCZYK A，MALINOWSKI M.Application of curvelet denoising to 2D and 3D seismic data：practical considerations[J].Journal of Applied Geophysics，2014，105：78-94.

[9] GAN S W，CHEN Y K，ZU S H，et al.Structure-oriented singular value decomposition for random noise attenuation of seismic data[J].Journal of Geophysics and Engineering，2015，12(2)：262-272.

[10] TANG G，MA J W，YANG H Z.Seismic data denoising based on learning-type overcomplete dictionaries[J].Applied Geophysics，2012，9(1)：27-32.

[11] PEYRE G，FADILI J.Group sparsity with overlapping partition functions[C]//19th European Signal Processing Conference.[S.l.:s.n.],2011：303-307.

[12] HUANG J Z，ZHANG T.The benefit of group sparsity[J].The Annals of Statistics，2010，38(4)：1978-2004.

[13] HUANG J Z，ZHANG T，METAXAS D.Learning with structured sparsity[J].Journal of Machine Learning Research，2011，12(7)：3371-3412.

[14] ZHANG L，MA C.Low-rank decomposition and Laplacian group sparse coding for image classification[J].Neurocomputing，2014，135(8)：339-347.

[15] MAIRAL J，JENATTON R，OBOZINSKI G，et al.Convex and network flow optimization for structured sparsity[J].Journal of Machine Learning Research，2011，12(3)：2681-2720.

[16] SUK H I，WEE C Y，LEE S W，et al.Supervised discriminative group sparse representation for mild cognitive impairment diagnosis[J].Neuroinformatics，2015，13(3)：277-295.

[17] LAZZARO D，MONTEFUSCO L B，PAPI S.Blind cluster structured sparse signal recovery：a nonconvex approach[J].Signal Processing，2015，109：212-225.

[18] ELAD M，AHARON M.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Transactions on Image Processing，2006，15(12)：3736-3745.

[19] AHARON M，ELAD M，BRUCKSTEIN A.K-SVD：an algorithm for designing over complete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing，2006，54(11)：4311-4322.

[20] ENGAN K，AASE S O，HUSOY J H.Method of optimal directions for frame design[C]//IEEE International Conference on Acoustics，Speech and Signal Processing.Washington,D.C.:IEEE Computer Society，1999：2443-2446.

[21] SZABO Z，POCZOS B，LORINCZ A.Online group-structured dictionary learning[C]//IEEE Conference on Computer Vision and Pattern Recognition.Washington,D.C.:IEEE Computer Society,2011：2865-2872.

[22] MEIER L，VAN DE GEER S，BUHLMANN P.The group lasso for logistic regression[J].Journal of the Royal Statistical Society：Series B (Statistical Methodology)，2008，70：53-71.

[23] YUAN M，LIN Y.Model selection and estimation in regression with grouped variables[J].Journal of the Royal Statistical Society：Series B (Statistical Methodology)，2006，68：49-67.

(责任编辑 张淑艳)

Seismic data denoising via adaptive learning-type group-structured dictionary sparse representation

XU Xiaohong, ZHANG Yang, QU Guangzhong, BI Yunyun

(School of Computer and Information， Hefei University of Technology， Hefei 230009， China)

The adaptive dictionary learned by seismic data can more accurately represent seismic data. According to the reason that the adaptive dictionary trained by traditional sparse representation method has no structure， an algorithm to suppress random noise of seismic data based on adaptive learning-type group-structured dictionary is proposed. The algorithm can be divided into three steps. The first step is to train an adaptive learning-type group-structured dictionary by seismic data. The second step is to represent seismic data by using the group-structured dictionary. The third step is to reconstruct seismic data by representation coefficients obtained from the second step. The group-structured dictionary used in the paper is able to adapt to the individual characteristics of seismic data， so more sparse representation coefficients can be obtained by using the group-structured dictionary to represent seismic data. The random noise coefficients can be removed effectively by using the group-structured dictionary to represent seismic data， so the algorithm proposed in the paper can effectively suppress random noise. The experimental results show that the algorithm proposed in the paper to suppress random noise of seismic data has a good denoising effect.

sparse representation; dictionary learning; group-structured dictionary; seismic data denoising

2015-12-18；

2016-02-06

国家重大科研装备研制资助项目(ZDYZ2012-1)

徐小红(1976-)，男，安徽望江人，博士，合肥工业大学副教授，硕士生导师.

10.3969/j.issn.1003-5060.2017.02.009

P315.01

A

1003-5060(2017)02-0186-06