山东半岛蓝色经济区经济—环境复合系统仿真与发展对策研究

董会忠++王格��

摘要：构建了以山东半岛蓝色经济区为例的经济—环境复合系统发展系统动力学模型，运用VENSIM软件对区域未来发展情景进行定量化动态研究与模拟。通过调节复合系统的决策变量，设定了4种不同的发展情景方案，预测在不同情景方案下山东半岛蓝色经济区的发展状况，得出山东半岛蓝色经济区经济—环境复合系统协调发展的最优方案，为山东半岛蓝色经济区的规划、治理和发展提供决策支持。

关键词：山东半岛蓝色经济区；系统动力学；决策变量；情景方案

DOI：10.13956/j.ss.1001-8409.2017.02.22

中图分类号：F205；F127 文献标识码：A 文章编号：1001-8409（2017）02-0103-06

Study on Simulation and Development Countermeasures of

Economyenvironment Composite System in

Shandong Peninsula Blue Economic Zone

DONG Huizhong，WANG Ge

（School of Business， Shandong University of Technology， Zibo 255012）

Abstract：This paper constructed a system dynamics model of composite system of environment and economic development taking Shandong Peninsula Blue Economic Zone as an example. It used the VENSIM software to do quantitative study and dynamic simulation on the future development situation of the region. By adjusting the composite decision variables of the system， it set up 4 different kinds of development scenarios and predicted the development status of Shandong Peninsula Blue Economic Zone in different scenarios， then get the optimal solution of Shandong peninsula blue economic zone on complex system of economy and environment coordinated development to provide decision support for the planning， management and development of Shandong Peninsula blue Economic Zone.

Key words：Shandong Peninsula Blue Economic Zone； system dynamics； decision variables； scenarios

区域协调发展涉及到社会、经济、资源、环境等诸多因素[1]，是多个子系统耦合演化的结果。许多地区在发展过程中仅仅关注经济发展速度，而忽视当地资源与环境承载力，造成资源的严重短缺和生态环境的普遍恶化，区域发展处于失衡状态，难以持续发展。当前，人们已普遍意识到以牺牲资源环境为代价的发展不可持续，努力探求社会经济与生态环境协调发展的途径已成为各国政府高度关注的焦点和众多学者研究的热点。作为一个复杂巨系统，区域经济—环境复合系统具有多变量、非线性、动态性和多重反馈的特性，系统动力学是研究复杂巨系统的科学方法，能够对不同情景方案下的区域发展态势进行有效研究，并对未来发展趋势进行科学预测。该方法在国外广泛应用于经济社会与生态环境研究领域[3-5]，代表文献有《增长的限制》和《趋向全球平衡》（以WORD Ⅲ模型为基础）[2]。上世纪80年代初，系统动力学方法被引入我国后普遍应用于国民经济、区域合作、可持续发展、技术创新等领域[6-11]。本文采用系统动力学仿真技术对山东半岛蓝色经济区环境经济复合系统进行仿真模拟，并对系统状态进行评估，定量研究半岛经济区经济—环境系统协调发展状态，对各种情景的作用和效果进行比较和分析，从而作出合理选择，为山东半岛蓝色经济区发展规划的制定提供科学依据。

1系统动力学模型构建

11研究区域边界确定

山东半岛蓝色经济区陆域面积64万平方千米，范围包括青岛、东营、烟台、潍坊、威海、日照6市及滨州的无棣、沾化2个沿海县所属陆域，海域面积1595万平方千米，包括山东全部海域。为研究方便，本文构建的模型及相关数据分析界定在青岛、东营、烟台、潍坊、威海、日照及滨州市全部区域。

12区域复合系统的结构分析及子系统划分

根据经济环境协调发展理论[12]，将山东半岛蓝色经济区经济环境复合系统划分为经济、人口、资源、环境四个子系统，各子系统内部要素相互作用，相互关联，形成一个动态复杂系统，以系统各变量之间的相互关系为基本框架，建立山东半岛蓝色经济区复合系统模型，通过调整决策变量，对预设发展模式进行仿真模拟，进而找到山东半岛蓝色经济区发展的最佳模式。

（1）经济子系统

经济子系统把能够反映经济发展水平的第一产业、工业、建筑业和第三产业产值作为流位变量（水平变量）；把第一产业GDP增加值、第三产业GDP增加值、建筑业GDP增加值和工业GDP增加值作为流率变量（速率变量）；把区域GDP、第一产业GDP增长率、第三产业GDP增长率、建筑业GDP增长率和工业GDP增长率等作为辅助变量。通过人均GDP、产业用水、工业COD排放量和工业氨氮排放量等輔助变量分别与人口、资源、环境子系统建立关联。“三产”比例是反映山东半岛蓝色经济区区域经济产业结构合理性的指标，因此以第一产业GDP增长率、工业GDP增长率和第三产业GDP增长率作为经济子系统的决策变量。通过以上指标建立经济子系统模型。包括14个方程和4个表函数，其中，主要方程有：

第一产业GDP=INTEG（第一产业GDP增加值，70731，单位：亿元）

建筑业GDP=INTEG（建筑业GDP增加值，38204，，单位：亿元）

工业GDP=INTEG（工业GDP增加值，317624，单位：亿元）

第三产业GDP=INTEG（第三产业GDP增加值，21111，单位：亿元）

区域GDP=第一产业GDP+第三产业产业GDP+建筑业GDP+工业GDP（单位：亿元）

工业GDP增长率=工业GDP增长率 LOOKUP（Time）

建筑业GDP增长率=建筑业GDP增长率 LOOKUP（Time）

第一产业GDP增长率=第一产业GDP增长率 LOOKUP（Time）

第三产业GDP增长率=第三产业GDP增长率 LOOKUP（Time）

（2）资源子系统

土地、水、能源及其他矿产等自然资源是人类社会发展的重要物质基础，自然资源的合理开发和利用对于区域协调发展具有重要意义。在资源子系统中，把可用水资源量和耕地面积作为水平变量；国家基建占地、退耕还林还草占地、乡村集体占地以及水资源可供量和工业用水量、农业用水量、生活用水量、水资源循环利用率，再用水回用率等作为辅助变量。通过生活用水量以及人均耕地面积与人口子系统建立关联，以生活污水处理回用量作为资源子系统和环境子系统沟通的桥梁。通过引入耕地压力指数模型[13]来考察山东半岛蓝色经济区耕地压力情况。耕地压力指数——最小人均耕地面积与实际人均耕地面积之比，其算法如下：

K=SminS（1）

式中K为耕地压力指数，Smin为最小人均耕地面积，即一定区域范围内保障食物需求的最小人均耕地面积，S为人均实际耕地面积。计算耕地压力指数时，在给出人均实际耕地面积的情况下，最小人均耕地面积是影响耕地压力指数的关键变量，其算法如下：

Smin=Gr×βP×Q×k（2）

式中，Smin为山东半岛蓝色经济区最小人均耕地面积，Gr为山东半岛蓝色经济区区域人均粮食需求量，β为山东半岛蓝色经济区区域粮食自给率，P为山东半岛蓝色经济区区域粮食单产，Q为山东半岛蓝色经济区区域粮食播种面积占总播种面积的比重，k为山东半岛蓝色经济区区域复种指数。

当K>1时，表明耕地压力明显，容易出现粮食危机，需要采取紧急必要措施降低耕地压力指数；当K<1时，表明耕地压力不明显，粮食生产处于安全范围之内；K=1时，最小人均耕地面积等于实际人均耕地面积，表明耕地压力开始显现，应当密切关注耕地面积的变化，采取措施避免耕地压力变大，确保粮食生产的安全。资源子系统方程有22个，表函数6个，主要方程有：

水资源量=INTEG（生产量-消耗量，1101，单位：亿立方米）

生活用水量=农村生活用水量+城镇生活用水量（单位：亿立方米）

工业用水量=工业GDP×工业亿元产值用水量（单位：亿立方米）

再用水回用量=生活污水处理量×再用水回用率（单位：亿立方米）

工业亿元产值用水量=工业亿元产值用水量 LOOKUP（Time）

城镇人均生活用水量=城镇人均生活用水量 LOOKUP（Time）

耕地面积=耕地增加量-耕地减少量（单位：公顷）

耕地压力指数=最小人均耕地面积/实际人均耕地面积

（3）人口子系统

人口子系统建模过程中选取总人口作为流位变量（水

平变量）；以年自然增长人口和年净迁入人口为流率变量（速率变量）；把农村人口、城镇人口、自然增长率、人口净迁入率作为辅助变量。人口子系统共有方程9个，3个表函数，主要方程有：

总人口=INTEG（年自然增长人口+年净迁入人口，528628，单位：万人）

城镇人口=总人口×城市化水平（单位：万人）

农村人口=总人口-城镇人口（单位：万人）

自然增长率=自然增长率 LOOKUP（Time）

人口净迁入率=人口净迁入率 LOOKUP（Time）

城镇化水平=城镇化水平 LOOKUP（Time）

（4）环境子系统

环境子系统建模过程中，选取COD存量和氨氮存量作为流位变量（水平变量）；以COD产生量、COD削减量，氨氮增加量、氨氮削减量为流率变量（速率变量）；以工业COD产生量、生活COD产生量、工业废水COD削减量、工业氨氮产生量、工业废水氨氮削减量、生活COD削减量、生活氨氮产生量、生活氨氮削减量、工业废水处理量、工业废水排放量、工业废水治理费用、工业亿元产值废水量等为辅助变量。选取COD和氨氮存量作为水环境污染程度的指示指标。环境子系统共有方程22个，表函数11个，主要方程有：

COD存量=INTEG（COD产生量-COD削减量，539793，单位：吨）

氨氮存量=INTEG（氨氮产生量-氨氮削减量，53538，单位：吨）

工业废水产生量=工业GDP×工业亿元产值废水量（单位：吨）

生活污水产生量=城镇人口×城镇居民人均生活污水产污系数（单位：万吨）

工业废水治理费用占工业GDP比重=工业废水治理费用占工业GDP比重 LOOKUP（Time）

城镇居民人均生活污水产污系数=城镇居民人均生活污水产污系数 LOOKUP（Time）

13經济—环境复合系统模型构建

通过对山东半岛蓝色经济区经济、社会、资源、环境子系统的结构分析，选取能够合理描述各子系统的变量，建立复合系统动力学模型（如图1所示）。

14模型有效性检验

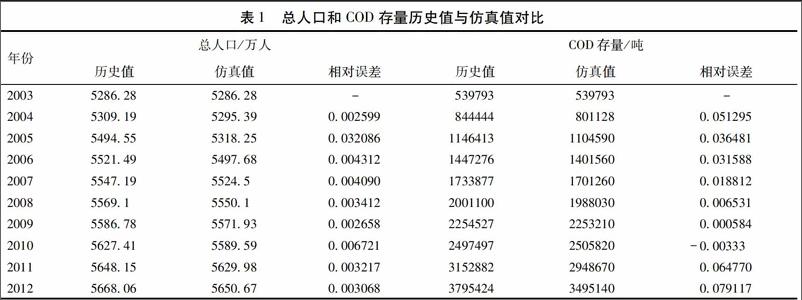
系统动力学通过Vensim软件建立系统动力学模型，对复合系统发展态势进行预测，其中模型的有效性检验是模型预测的关键环节。本模型模拟运行时间为2013～2020年，以2013年为基准年，仿真步长为1年，模型有效性检验采用的历史统计数据主要来源于《山东省统计年鉴》以及各市统计年鉴。以2003～2012年历史数据为检验依据，其中某些指标如年净迁入率、自然增长率、城镇居民人均COD产污系数等是根据2003～2012年所收集数据计算得出，某些指标随着时间的推移而变化，这些指标采用表函数的形式给出，而变量间关系不明确的指标也是采用表函数形式给出。本文采用相对误差法对半岛蓝色经济区复合系统模型模拟的结果进行检验，以总人口和COD存量两个水平变量为主要例证，检验结果如表1，通过表1可以看出，2003～2012年总人口和COD存量的仿真值和历史值的相对误差介于-1%～51295%之间，拟合精确度较高，相对误差检验结果比较理想。

2山东半岛蓝色经济区模型预测与分析

21情景设定

在对2003～2012年数据有效性检验的基础上，本文设定不同的决策变量来调控2013～2020年山东半岛蓝色经济区区域经济发展的模式。选取第一产业GDP增长率、工业GDP增长率、第三产业GDP增长率作为调整经济结构的决策变量，将工业废水治理费用占工业GDP的比重、再用水回用率以及农业亿元产值用水量作为调控环境和资源的决策变量。由于实际人均耕地面积与人口基数有很大关系，在耕地面积逐年减少、人口不断增加的情况下，实际人均耕地面积呈现逐年减少的状况，因而最小人均耕地面积成为影响耕地压力指数的关键变量；在粮食自给率为1，粮食单产保持2012年的水平上，复种指数成为影响最小人均耕地面积的关键变量。根据山东省三次产业比重调整战略，提高第三产业比重，降低第一、二产业比重的方向，设定出四种发展模式情景：

情景Ⅰ：设定第一产业GDP增长率降低25个百分点，从2013年的11%下降到2020年的85%；工业GDP增长率增加17个百分点，从2013年53%增加到2020年的7%；第三产业GDP增长率小幅度稳步提高，增加29个百分点，从2013年的127%增加到2020年的156%；工业废水治理费用占工业GDP的比重和复种指数以及农业亿元产值用水量维持在2012年的水平，再用水回用率从2013年到2020年提高6个百分点。

情景Ⅱ：设定第一产业GDP增长率2016年降低到情景Ⅰ2020年85%的水平，到2020年降低到62%；工业GDP增长率略微降低，2013年到2020年降低08个百分点；第三产业GDP增速与情景Ⅰ相比较明显，2016年达到情景Ⅰ2020年156%的水平，到2020年第三产业GDP增长率达到175%；工业废水治理费用占工业GDP的比重、再用水回用率、复种指数均稳步提升；农业亿元产值用水量略微降低。

情景Ⅲ：设定第一产业GDP增长率降低幅度与情景Ⅰ相似；工业GDP增长率明显降低，2016年降低到情景Ⅱ2020年45%的水平，到2020年工业GDP增长率降低到40%；第三产业GDP增速明显提高，2016年达到164%，2020年达到185%；再用水回用率以及复种指数在情景Ⅱ的基础上继续提高，工业废水治理费用占工业GDP的比重略微提升，与情景Ⅱ相似，农业亿元产值用水量在情景Ⅱ的基础上继续降低。

情景Ⅳ：第一产业GDP增长率、工业GDP增长率显著降低，降幅较情景Ⅱ相比较大。其中，第一产业GDP增长率到2020年降低到43%，工业GDP增长率降低到35%；第三产业GDP增长率显著提高，到2020年第三产业GDP增长率达到268%，工业废水治理费用占工业GDP比重显著增加，再用水回用率、复种指数显著提高，与情景Ⅲ相比提升幅度较大，农业亿元产值用水量明显减少。

22模拟结果分析

情景模拟结果分析目的在于找出适合山东半岛蓝色经济区的较为理想的发展模式，因而指标变量的选取至关重要，它能够反映区域复合系统的基本情况。图2至图5为模型运行得出的指标变量变化趋势图，表3为模型运行得出的各项指标模拟值。

从仿真模拟出的结果可以看出：

情景Ⅰ发展模式是逐步降低第一产业GDP增长率，略微增加工业GDP增长率，同时第三产业GDP增长率稳步提高；工业废水治理费用占工业GDP比重、复种指数、农业亿元产值用水量维持在2012年的水平。从模拟结果可以看出，区域GDP增速从2016年开始增幅略高于目前发展模式；COD存量与目前发展模式相比无明显差异；可用水资源量下滑趋势明显降低，低于目前发展模式下的水资源量，供水形势严峻，2016年供水缺口为1375亿立方米，2020年供水缺口达到2891亿立方米；耕地压力指数与现状相比，无明显变化，耕地压力形势严峻，容易产生粮食危机。

情景Ⅱ发展模式是在稳步降低第一、二产业GDP增长率的前提下，在情景Ⅰ的基础上提高第三产业GDP增长率的速度；同时工业废水治理费用占工业GDP比重、复种指数稳步提高，再用水回用率从2013年的40%提高到2016年的45%、再到2020年的48%，农业亿元产值用水量减少缓慢。从模拟结果可以看出，区域GDP与情景Ⅰ相比，无明显差别，但增速略高于情景Ⅰ；COD存量增长趋势趋于平缓，明显低于情景Ⅰ，到2020年COD存量为54741万吨，明显低于情景ⅠCOD存量2020年87036万吨的水平；可用水资源量减少趋势明显低于情景Ⅰ，但供水缺口仍然存在，2016年供水缺口为105亿立方米，2020年供水缺口为2211亿立方米，耕地压力指数呈现降低趋势但依然高于1，耕地压力依然明显。

情景Ⅲ发展模式是第一、二产业GDP增长率降幅与情景Ⅰ相似，但低于情景Ⅱ，第三产业GDP增长率较情景Ⅱ相比增幅较大，2016年第三产业GDP增长率为164%，2020年为185%；同时工业废水治理费用比重提高，与情景Ⅱ相比，无明显差别，再用水回用率2016年提高到48%，2020年達到50%，农业亿元产值用水量降低幅度高于情景Ⅱ。从模拟结果可以看出，区域GDP增速略高于情景Ⅰ和情景Ⅱ；COD存量增速明显低于情景Ⅰ和现状发展模式，但高于情景Ⅱ，可用水资源量降幅低于情景Ⅱ，耕地压力指数明显低于情景Ⅱ， 2020年耕地压力指数为126，耕地压力依然存在。

情景Ⅳ发展模式是明显降低第一、二产业增长率，同时大幅提高第三产业GDP增长率，到2016年，第三产业GDP增长率为185%，2020年达到268%；工业废水治理费用比重明显加大，再用水回用率、复种指数明显提高，农业亿元产值用水量明显降低。从模拟结果可以看出，区域GDP增长幅度明显高于情景Ⅰ、Ⅱ、Ⅲ，区域GDP规模2016年为417429亿元，2020年达到942623亿元，人均GDP明显提高；COD存量大幅度降低，从2016年开始COD存量开始降低，到2020年，COD和氨氮治理明显，水环境明显改善， 2016年供水缺口为695亿立方米，2020年供水缺口为1176亿立方米，间接提高了水资源可用量；耕地压力指数2020年为098，低于1，耕地压力明显改善。

3结论与建议

根据以上分析可以得出在情景Ⅰ中虽注重产业结构调整，但产业结构调整比例不明显，COD和氨氮环境压力形势较现状发展更加严峻，耕地压力指数较大，耕地压力明显；情景Ⅱ调整了经济产业结构，第一产业增速降低，第二产业增速小幅增高，第三产业增速较情景Ⅰ稳步提高，同时提高环境治理费用，提高再用水回用率，环境压力明显减小，但可用水资源量的紧张程度依然明显，供水缺口比情景Ⅰ有所减少，耕地压力指数与情景Ⅰ相比虽有所下降，但依然高于1，耕地压力明显；情景Ⅲ第一、二产业增速逐步降低，第三产业增速有较大提高，环境治理费用比重、再用水回用率、复种指数提高，农业亿元产值用水有较明显的减少，环境压力比情景Ⅰ明显缩小，与情景Ⅱ相比有小幅增加，供水缺口低于情景Ⅰ、Ⅱ，水资源紧张程度依然存在；情景Ⅳ是着重加大产业结构调整，明显降低第一、二产业增长速度，大幅提高第三产业增长速度，环境治理投资比重增大，再用水回用率明显提高，农业亿元产值用水量明顯较少，到2020年，区域经济产值达到942623亿元；COD存量2016年为471253万吨，到2020年COD存量基本消除，COD和氨氮治理明显，水环境压力明显改善；供水缺口2016年为695亿立方米，2020年为1176亿立方米，有效缓解了水资源紧张程度。通过以上结论，推荐情景Ⅳ为山东半岛蓝色经济区发展方向的最优情景。

通过上述四种情景发展模式的仿真模拟结果，提出如下建议：（1）结合山东半岛蓝色经济区6市差异，进一步推动产业结构优化升级，降低第一、二产业的比重，大力提高第三产业比重，推动宏观产业结构优化，形成合理的产业结构发展模式，以进一步提高经济发展的质量和效益；（2）以“保持经济平稳增长、水资源消耗低增长”为发展模式，推进节水减排计划，合理分配水资源用水量在各产业结构中的比例；（3）出台相关的政策和提高排污标准，制定相应的评价体系，通过增加工业废水治理费用，大力发展废水再回用水的循环利用率，从而达到减少水环境污染、增加水资源量的双重效果。

参考文献：

[1]覃成林. 区域协调发展机制体系研究[J]. 经济学家， 2011， （4）： 63-70.

[2]王其藩. 系统动力学[M].2009年修订版. 上海：上海财经大学出版社， 2009.

[3]Forrester J W. The System Dynamics National Model： Macrobehavior from Microstructure Modeling Growth Strategy in a Biotechnology Startup Firm [J].System Dynamics Review， 1989， 7（2）： 93-116.

[4]S M Disney A，T Potter， B M， Cardner. The Impact of Vendor Managed Inventory on Transport Operation [J].Transportation Research E， 2003.

[5]Marquez A C， Bianchi C， Gupta J N D. Operational and Financial Effectiveness of Ecollaboration Tools in Supply Chain Integration[J]. European Journal of Operational Research，2004.

[6]张建慧，雷星晖，李金良. 基于系统动力学城市低碳交通发展模式研究——以郑州市为例[J]. 软科学， 2012， 26（4）： 77-81.

[7]陈国卫，金家善，耿俊豹. 系统动力学应用研究综述[J]. 控制工程， 2012， 19 （6）：921-928.

[8]李维乾，解建仓，李建勋，等. 基于系统动力学的闭环反馈水资源优化配置研究[J]. 西北农林科技大学学报（自然科学版）， 2013， 41（11）：209-216.

[9]贾一伟. 基于系统动力学的高校科技产业可持续发展研究[D]. 北京交通大学， 2013.

[10]谭术魁，张路，齐睿. 基于系统动力学的区域耕地压力指数研究[J]. 自然资源学报， 2012， 27（5）：757-765.

[11]李华，蔡永立. 基于SD的生态安全指标阈值的确定及应用——以上海崇明岛为例[J]. 生态学报， 2010， 30（13）： 3654-3664.

[12]刘伟，陈超凡，桓汉青，等. 基于系统动力学模型的低碳城市发展研究[J]. 环境污染与防治， 2014， 36（4）： 86-91.

[13]蔡运龙，傅泽强，戴尔阜. 区域最小人均耕地面积与耕地资源调控[J]. 地理学报， 2002， 57（2）： 127-134.

（责任编辑：辜萍）