元胞自动机模型在交通流中的应用研究

姚层林++左传

摘要：由于目前交通状况带来的诸多问题，通过科学理论的指导增进对交通系统的管理和控制，充分利用其资源，减轻环境污染并解决其他问题，达到安全与便捷的较好统一。元胞自动机模型已广泛应用于交通领域的研究，它的建立是描述和模拟复杂交通系统的最好方法。根据不同道路的交通情况，构建交通流模型，以定量的视角理解交通拥堵的成因。交通状况随着社会发展而不断变化，元胞自动机在交通系统的应用，对于推动元胞自动机模型的改进和完善交通运输情况具有重要意义。

关键词：元胞自动机模型 交通流理论 应用研究

中图分类号：TP23.U491 文献标识码：A 文章编号：1007-9416（2016）10-0080-03

元胞自动机（Cellular Automata，简称CA）实质上是定义在一个具有离散、有限状态的元胞组成的元胞空间上，并按照一定的局部规则，在离散的时间维度上演化的动力学系统。实际上，著名计算机科学家Von Neumann早在1968年就提出元胞自动机基本思想[1]。他提出模仿人脑的行为，人脑包含自控制和自维护机理，这个元胞系统按照离散时间进行演化。Wolfram提出了元胞自动机的动力学分类方法，1986年，M.Cremer和J.Ludwig将CA最早应用于交通系统[2]的研究。元胞自动机从产生以来，被广泛地应用到生物学、生态学、物理学、化学、交通科学等多个领域。交通系统是一个十分复杂、具有不确定性的系统，CA的特点与交通流的特点极其相似，决定了CA在交通领域应用的合理性。用CA对交通系统进行模拟，体现交通流的变化特征，寻找交通流的规律，揭示交通拥堵产生的机理，进而有效地改良交通运输状况。

1 CA基础理论

1.1 构成

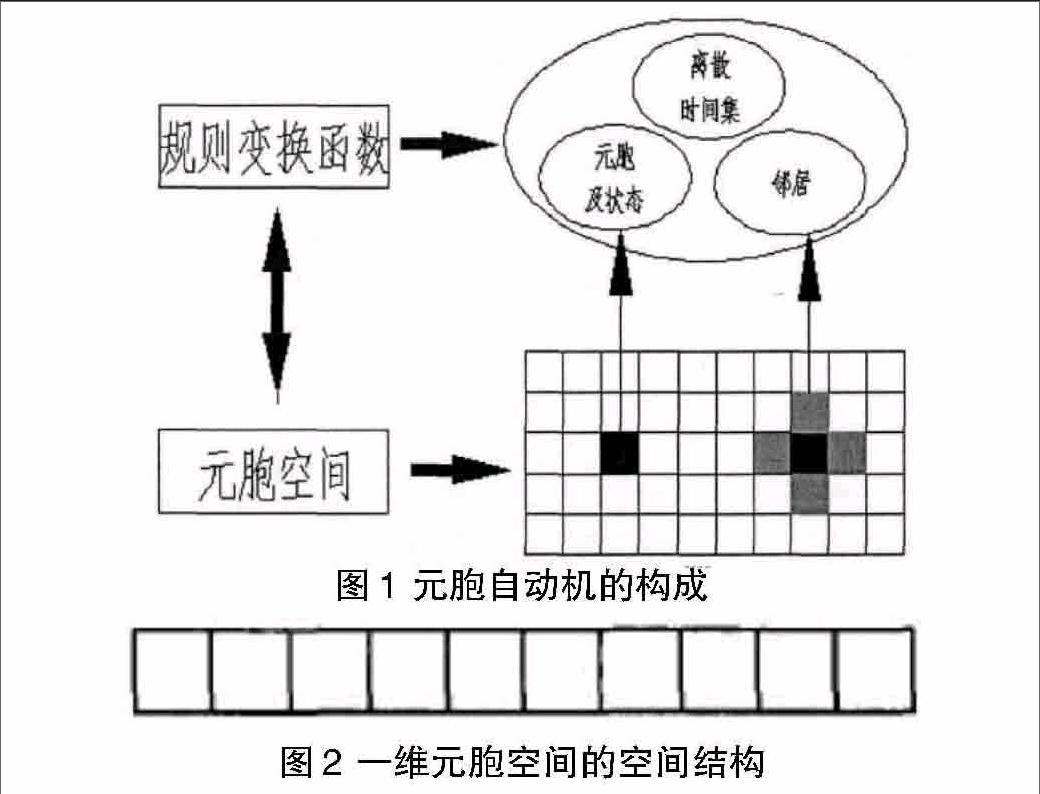
CA最基本的组成单元是元胞、元胞空间、邻居及规则四部分，另外还应包括元胞的状态和时间，如图1所示。可以将CA视为一个元胞空间和定义于该空间的变换函数所组成。

1.2 元胞

CA最基本的组成部分就是元胞，又称为单元、细胞或基元，离散地分布于一维、二维或多维欧几里得空间的晶格点上。某一时刻，每个元胞都有自己的状态。

1.3 元胞空间

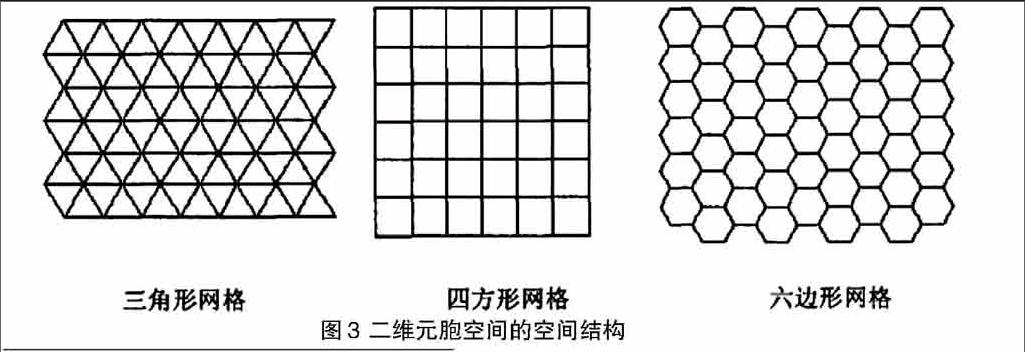
元胞在空间中分布的网格点的集合就是元胞空間。目前研究多集中在一维和二维元胞自动机上。一维元胞自动机的元胞空间只有一种划分，二维元胞自动机通常有三种划分方式：三角形、正方形和正六边形，如图2、图3所示。对于高维的元胞自动机，元胞空间的划分则可能有多种形式。

1.4 邻居

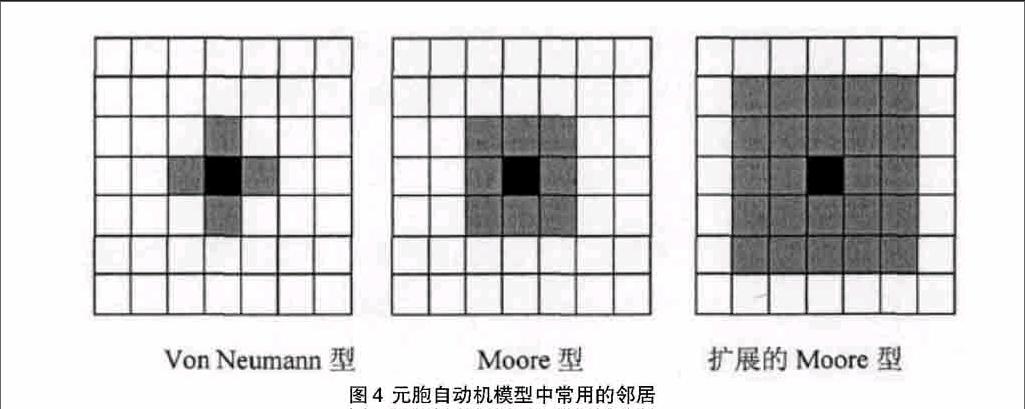
在元胞自动机中，一个元胞下一时刻的状态决定于本身状态和它的邻居元胞的状态。通常以半径来确定邻居，距离一个元胞内的所有元胞均被认为是该元胞的邻居。二维元胞自动机通常有以下几种邻居：Von Neumann型、Moore型和扩展的Moore型，如图4所示的结构。

1.5 边界条件

理论上，元胞空间通常是在各个维度上无限延展的，但是在实际应用中，理论条件无法在计算机上实现，所以需要定义不同的边界条件。

1.6 演化规则

演化规则是根据元胞当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数，简单来说，就是一个状态转移函数。记为+1=f（，），我们称f为元胞自动机的局部映射，为t时刻i元胞的邻居元胞状态[3]。

2 元胞自动机的一般特征

从元胞自动机的定义及构成分析，元胞自动机具有如下特征[4]：同质性、齐性；时间离散；空间离散；状态离散有限；同步计算；时空局域性；维数高。元胞自动机的价值取决于其演化规则，体现在元胞的动力学系统的内涵。

3 交通流理论

3.1 交通流基本参数的关系

交通流基本参数有交通流量、车辆速度、车辆密度、车头间距和车头时距等，在实际的研究领域中，最重要的三个基本参数是交通流量、行车速度和交通密度。交通流量，即单位时间内通过交通道路某断面的车辆数，用符号q表示；行车速度为道路上车辆行驶速度的平均值，用符号v表示；交通密度，即某一瞬间单位长度的车道上行驶的车辆总数，用符号k表示。三者之间的关系可表示为：q=v×k（q、v、k的单位分别是辆/小时、公里/小时和辆/公里，这一关系式称为交通流基本模型）。

3.2 交通实测现象

3.2.1 交通堵塞

交通堵塞是一种常见的、研究广泛的交通现象。日常生活中人们理解的堵塞和交通流理论中的堵塞有一定的区别：通常人们理解的车速远远低于最大车速、车流量非常低时才是堵塞；而在交通流理论中，只要车辆以低于最大值的速度行驶且车道出现集簇现象，就称之为堵塞。实测的交通堵塞，大多发生在交通瓶颈的上游；比如道路缩减和交叉路口的上游[5]。交通瓶颈处，主干道的车辆密度增大，道路的局部通行能力降低，使得瓶颈的上游易处于交通拥堵状态；一段时间的交通疏导使得车辆逐渐恢复正常行驶，所以瓶颈的下游多为典型的自由流状态。此外，交通事故易导致车辆聚集，也是产生堵塞的一个原因。

3.2.2 自组织现象

自组织现象是指系统通过系统内部各子系统之间的非线性相互作用，在一定的条件下，自发产生在时间、空间和功能上稳定的结构。在真实的交通中，存在着一定的密度区域，在该区域内交通流的状态是亚稳定的，由于车辆之间的相互作用，一些交通流的状态会自发形成[6]。比较典型的是向后传播的堵塞波的形成，这种堵塞的特点有：（1）产生堵塞的随机性；（2）堵塞幅度的不断变化；（3）堵塞会消失。一般来说，这种现象易发生在入口、出口匝道等瓶颈处。

4 交通应用

车辆组成的交通流实质是一个离散系统，而又紧密相互联系，导致复杂的交通现象。元胞自动机模型是交通流模型的理论基础，能够从微观层面分析复杂交通系统的研究工具。184号模型是以Wolfram命名的最基本的一维元胞自动机模型，其中包含的基本要素能够实现一些交通现象的模拟，但是不能完全适应复杂的实际交通状况。目前交通流的元胞自动机大致可分为两大类：以NS模型为代表的研究高速公路的模型，以BML模型为代表的研究城市网络交通的模型，这两类模型是对184号模型的进一步完善和发展。

4.1 NS模型

NS模型，由一维CA模型简化而来，于1992年由德国学者Nagel和Schreckenberg提出[7]。

在NS模型中，时间、空间和车辆速度都被整数离散化，道路被划分为等距离的离散的格子，即元胞，并且每个元胞或者是空的，或者被一辆车所占据，车辆n行驶的速度为Vn（t），速度可以取0，1，2，……，Vmax，Vmax是行驶车辆在道路上的最大行驶速度。车辆n和其前车n-1在时间步t的位置用Xn-1（t）和Xn-1（t）表示，dn（t）代表车辆n与其前车的车间距，即dn（t）=Xn-1（t）-Xn-1（t）-1。Pn（t）为车辆n在时间步t时随机慢化过程中的减速概率。ΔVn（t）是车辆n与其前车n-1的行驶速度之差，即ΔVn（t）=Vn（t）-Vn-1（t）。该模型以如下规则演化：

（1）加速，Vn（t+1）→min（Vn（t）+1，Vmax），表示驾驶员期望以最大速度驾驶车辆；

（2）减速，Vn（t+1）→min（Vn（t+1），dn（t）），表示避免与前车发生事故；

（3）随机慢化，以减速概率P使车辆的行驶速度Vn（t+1）→max（Vn（t+1）-1，0），表示实际的交通情况下各种不确定的因素使得减速行驶；

（4）运动，Xn（t+1）→Xn（t）+Vn（t+1），车辆位置更新，速度调整，继续向前运动。

NS模型具有简单的形式，仅用4条演化规则就表达出车辆行驶的不同情况。为了能够描述更多复杂的交通现象，在NS模型的基础上衍生和发展了许多模型，比如通过改进慢化规则，提出慢启动模型，巡航控制极限模型；通过改进加速规则，提出FI模型；以及考虑前车速度效应的模型，舒适驾驶模型等等。

4.2 BML模型

一维高速公路交通流模型很难模拟出二维城市交通系统的复杂的道路网结构，而BML模型实现了复杂路网结构的模拟。1992年，O.Biham，A.Middleton和D.Levine[8]三位学者提出一种元胞自动机模型（BML模型）用来模拟城市道路的交通现象，研究了交通堵塞的问题。简单形象的BML模型定义在一个N×N的方形格点网络中，点阵上分布着仅有东西方向和南北方向行驶的数目相等的两种车辆，每个格点可以拥有一辆南北方向行驶的车辆，也可以有一辆东西方向行駛的车辆，还有一种可能就是没有车辆占据。在每一个奇数时间步内，南北方向的车辆可以向前进一格；在每一个偶数时间步内，东西方向的车辆可以向前进一格；若车辆前方的格点以被其他车辆占据，因此这辆车只能保持静止不动。在这种情况下，两个方向的车辆分别在奇偶时间步内行驶，每个格点相当于信号控制的交叉路口，反映出交通信号灯的作用。

4.3 NS和BML耦合模型

BML模型不能完整地体现实际交通情况，表现在：（1）BML模型只有两个车流运动方向，未考虑其它转动方向；（2）BML模型中网络没有路段，只有交叉口。1999年，Chowdhury和Schadschneider等学者提出了一个更符合实际的W×W条道路组成的路网。基于BML模型，将两个相邻交叉口之间的路段（包括其中的一个交叉口）划分为D个元胞。因此每一条道路有W×D个元胞。在任意时刻，每一个元胞或者保持静止，或者被其他车辆占据。当D=1时，路网结构为BML模型。如图5所示，其中N=5，D=8东西方向和南北方向车辆分别用符号→和↑表示。

在该组合模型中，堵塞产生的内因与NS模型相近，系统自发的堵塞现象与BML模型十分类似。

5 结语

以上对应用前景进行了分析，建立了符合交通实际情况的模型，结果体现出：（1）通过元胞自动机在交通中的研究，可以形象地模拟出交通路口车辆的通行情况。（2）构建的元胞自动机模型具有时间、空间的离散性，决定了它在交通领域的重要价值。（3）城市交通网络受多种因素影响，交通拥堵的成因及分布十分复杂，还有许多问题未考虑。可以从更大网络规模、更符合实际的交通流量开展进一步研究。

参考文献

[1]V.Neumann.Celluar automata[M].New York：Academic Press，1968.

[2]S.Wolfram.Statistical mechanics of celluar automata[J].Rev.Mod.Phys.1983，55：601-644.

[3]B.Chopard and M.Droz.Celluar Automata Modelling of physical systems，//祝玉学，赵学龙（译）.物理系统的元胞自动机模拟.北京：清华大学出版社，（2003）.

[4]谢惠民.非线性科学从书：复杂性与动力系统.上海：上海科技教育出版社，（1994）.

[5]C.F.Daganzo，M.J.Cassidy，R.L.Bertini.Possible explanations of phase transitions in highway traffic [J].Transp.Res.A，1999，33：365-379.

[6]B.S.Kerner.Experimental features of self-organization in traffic flow [J].Phy.Rev.Lett，1998，81（17）：3797-3800.

[7]K.Nagel，M.Schreckenberg.A celluar automaton model for freeway traffic [J].J.Phys.I（France）1992，2：2221-2229.

[8]O.Biham，A.A.Middleton，D.A.Levine.Self-organization and a dynamical transition in traffic flow models[J].Phys.Rev.A 1992，46：R6124-R6127.

收稿日期：2016-08-26

基金项目：武汉市社科基金项目《大规模建设背景下的武汉道路拥堵区域疏散管理研究》（项目编号：14021）研究成果。

作者简介：姚层林（1972—），男，山东日照人，教授，高级工程师，毕业于华中科技大学硕研，研究方向：交通运输工程、高等教育管理等。