基于鲁棒的认知无线电功率分配算法

朱 孟， 王宏志， 周明月， 柏 杨

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)



基于鲁棒的认知无线电功率分配算法

朱 孟， 王宏志， 周明月*， 柏 杨

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

考虑授权用户的干扰功率阈值,认知用户的总发射功率预算和各个SU的信干噪比，提出了一种基于鲁棒的多用户认知无线电能量有效的功率分配算法。利用凸优化的相关理论，采用拉格朗日算法得到增益最坏情况下的功率分配。仿真结果证明了该功率分配算法的可行性和有效性。

认知无线电； 功率分配； 鲁棒优化

0 引 言

广泛应用的无线电技术正在深刻影响并改变着人们的日常生活，iphone、智能穿戴、电子阅览等电子设备已经成为生活中不可缺少的物品。各种无线设备的应用都不能脱离频谱。无线服务需求的增加，使得频谱资源变得匮乏和日益拥挤，亟需一种通信技术能够有效地解决这一困境。认知无线电(Cognitive Radio, CR)作为能够缓解频谱资源匮乏的新技术在无线通信领域获得了广泛应用，CR技术能够有效利用空闲频谱和低利用率频谱，从而可以极大地提高无线频谱利用率[1]。

在认知无线电网络中，通过合理调整SU发射机的工作功率，获得SU满意的用户服务质量(Quality of Service, QoS)[2]。关于功率分配，很多学者从减少能耗、最大化能量效率和认知网络容量的角度进行研究[3-6]。考虑多波段多天线的认知无线电网络，研究最小化SU的总功率消耗问题[3]。M H Islam[4]等提出了一种波束形成的分布式功率控制算法来解决最小化SU功耗问题。考虑认知无线电网络中能量博弈的层次结构，Lasaulce[5]等研究SU的能量效率的最大化问题。针对共享频谱的认知网络吞吐量最大化问题，Stotas[6]等介绍了一种新的接收器和帧结构的频谱共享认知无线电网络，来达到提高系统吞吐量的需求。这些算法都没有考虑认知系统的动态特性，即没有考虑信道参数的扰动，不符合认知系统的实际状况。

文中研究认知无线电网络中能量有效的功率分配问题。在满足PU的干扰功率阈值、SU的总发射功率预算和各个SU的SINR需求的前提下，考虑信道增益的扰动，实现认知系统SU发射功率的最小化。

1 系统模型和问题规划

文中研究Ad-Hoc的认知无线电网络，其中包括了多个分布式认知链路，M个SU和N个PU共享授权频谱。在分布式资源分配模型进行功率分配时，考虑了信道增益的扰动。假设通过感知方法，每个SU可以准确获得它们的位置信息，这些信息可以通过反馈信道传输到相应的发射机。

当SU与PU共享同一授权频段时，SU产生的干扰要小于PU接收机所能承受的门限阈值：

(1)

式中：hi----链路i上SU发射机与PU接收机之间的信道增益；

pi----链路i上SU发射机的工作功率；

Ith----PU所能承受的干扰功率阈值。

认知无线电网络中，PU是频谱的拥有者，SU是通过伺机方式接入的用户，SU总的发射功率要低于其自身的门限阈值，有：

(2)

式中：pmax----SU发射机总的工作功率上限值。

为了保证SU的QoS，每个SU的SINR必须高于某一目标值来保证用户可靠的信息传输。因此，每个SU的SINR应严格满足：

(3)

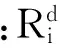
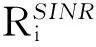
(4)

式中：hij----链路j上SU的发射机到链路i上SU的接收机之间的信道增益；

pj----链路j上SU发射机的工作功率；

Ipi----PU发射机对链路i上SU接收机产生的干扰，Ipi=p0Gi；

p0----PU发射机的工作功率；

Gi----PU发射机与链路i上SU接收机之间的信道增益；

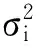
SINR的问题可以写成如下形式：

(5)

在满足限制条件(1)、(2)和(3)情况下，能量有效的功率分配问题的数学模型如下：

(6)

2 鲁棒分布式功率分配算法

在实际认知无线电网络中，信道增益的扰动会给SU带来较大的不确定性。针对这种不确定性，鲁棒算法可以使其免受数据不确定性的影响，实现认知网络的可靠通信。根据信道增益扰动的特性，考虑worst-case的情况进行鲁棒规划。

根据Cauchy-Schwarz不等式[7]，考虑信道增益扰动最大时，能量有效的功率分配问题的数学模型转化为：

(7)

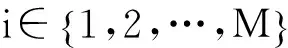
ε,η,φ----分别表示信道增益hi,χij,Gi最坏情况下的扰动值。

可以知道上述问题是一个凸优化问题[8]，运用Lagrange对偶算法解决，得到最优功率分配。则Lagrange函数如下：

(8)

式中：λi,μi,νi----分别为PU的干扰功率阈值、SU总发射功率预算和各个SU的SINR需求的Lagrange乘子。

根据次梯度更新算法，Lagrange乘子的更新函数如下：

(9)

其中α,β,γ为更新函数的步长，t为更新时间间隔，(·)+=max(·,0)。

相应的Lagrange次梯度函数表示为：

(10)

根据上面的论述与推导，考虑KKT(Karush Kuhn Tucker)条件下[8-10]，对于给定的λi,μi,νi最优解为：

(11)

式(11)即为用户i的最优的功率分配。

3 仿真结果与分析

3.1 仿真参数设定

运用仿真软件Matlab进行仿真验证来支持上述的理论分析。假设Ad-Hoc网络中有3个SU和1个PU，PU所能承受的干扰功率阈值为0.85 mW，SU总发射功率预算为1.50 mW，各个SU的目标SINR分别为6.85,7.60,8.30 dB。具体的仿真参数设定见表1。

表1 具体参数设定方案

3.2 仿真结果的性能分析

非鲁棒方案和鲁棒方案的功率收敛情况和容量比较情况如图1所示。

(a) 功率收敛情况

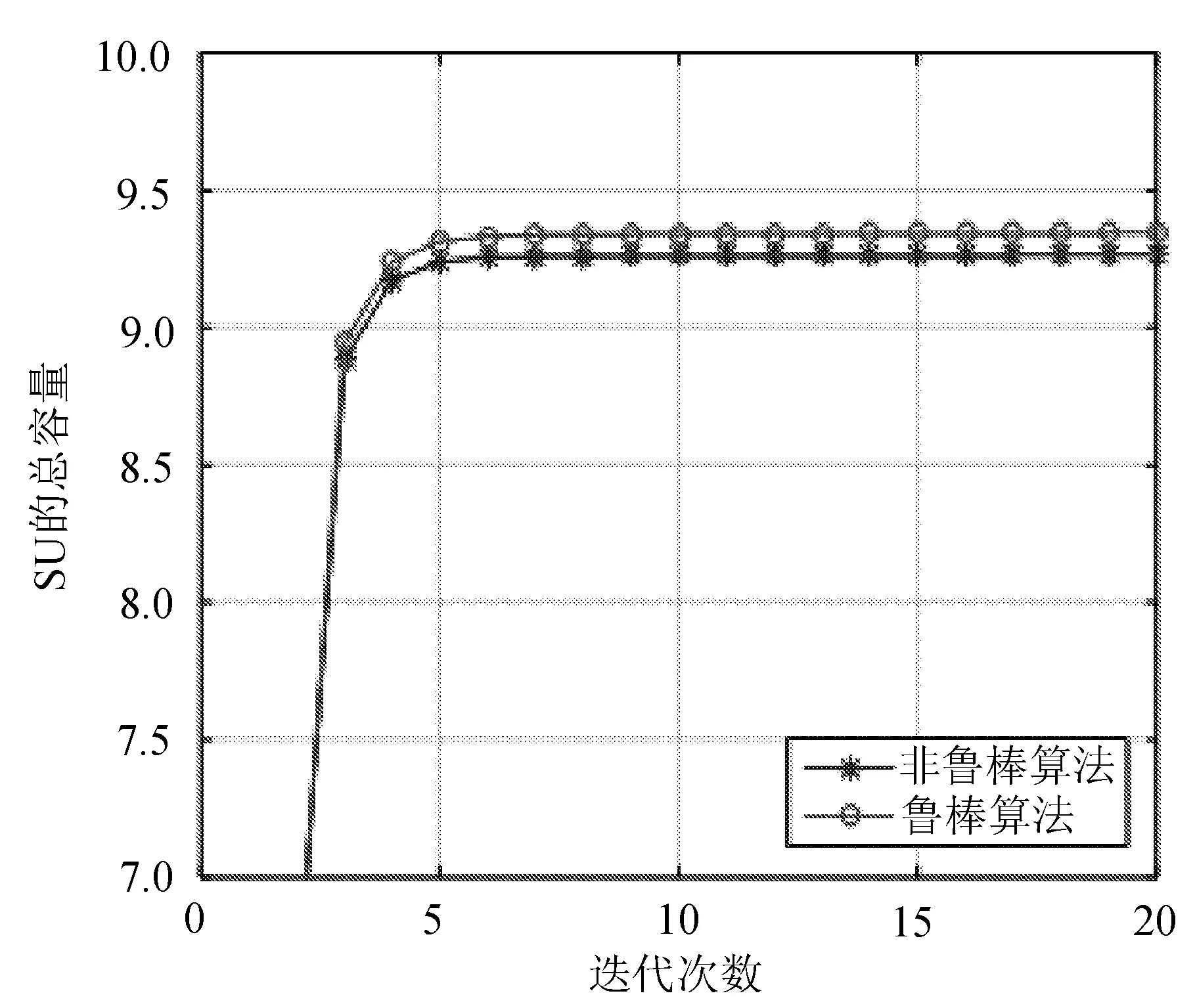
(b) 容量比较

图1 两种方案下的功率收敛和容量比较情况

功率迭代过程中非鲁棒方案主要考虑完美信道估计，而鲁棒方案根据实际信道情况考虑参数的不确定性。从图中可以看出，二者的功率值都很快趋于稳定，鲁棒方案下的功率分配为了抵消信道增益扰动的影响，适当提高功率值，系统的容量也会增加，这是鲁棒性和功率消耗之间的一个权衡。

非鲁棒方案与鲁棒方案对PU产生干扰的性能比较如图2所示。

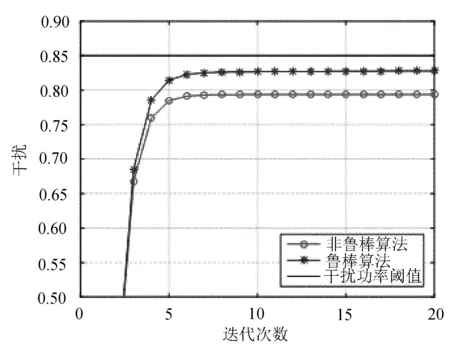
图2 两种方案下对PU产生干扰的性能比较

在信道增益存在扰动的情况下，非鲁棒功率分配方案以完美信道估计状况下的最优功率进行干扰功率运算，给PU带来的干扰能够满足PU的需求。鲁棒功率分配方案带给PU的干扰也满足系统需求。

非鲁棒方案与鲁棒方案总功耗的性能比较如图3所示。

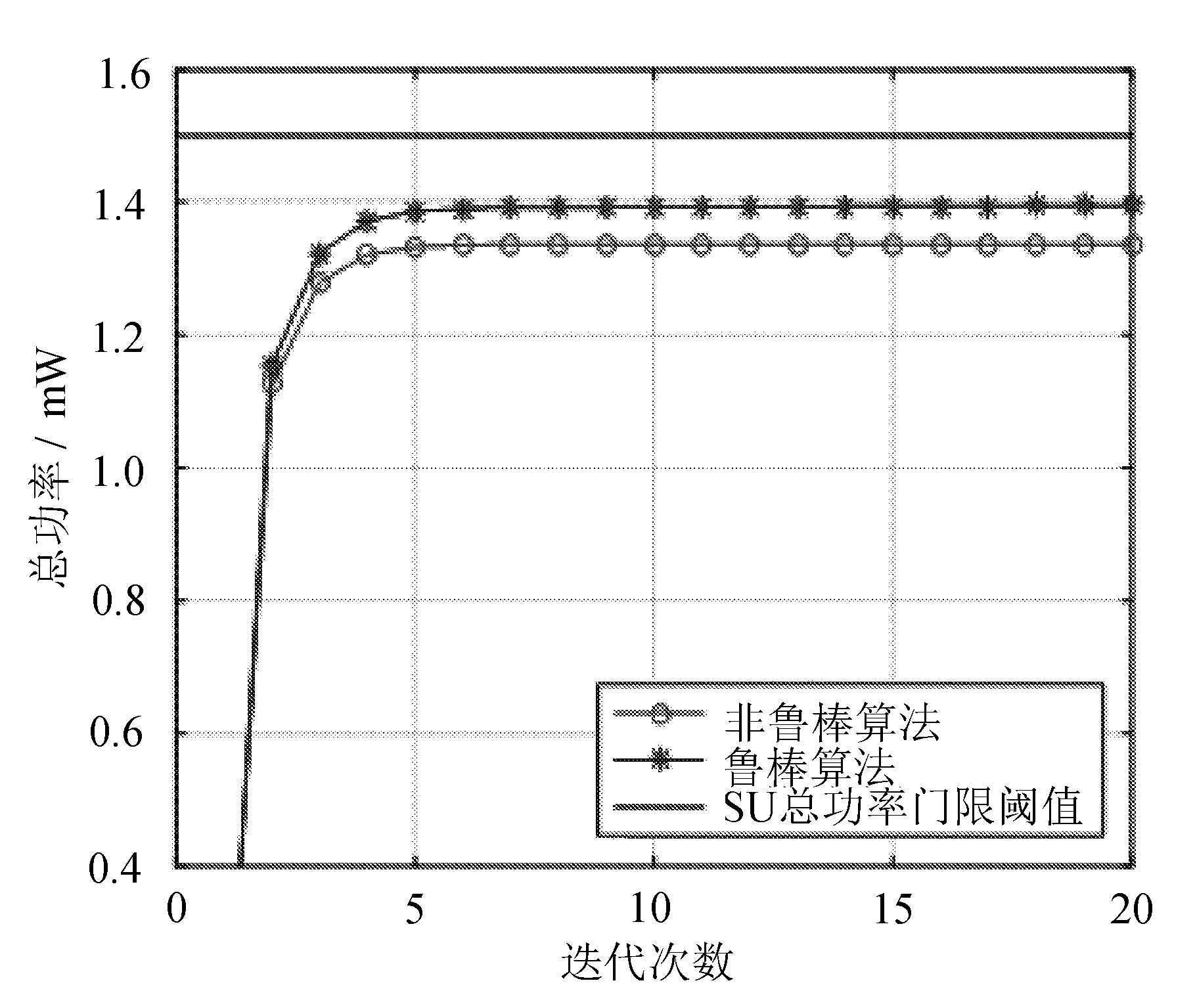
图3 两种方案下总功耗的性能比较

非鲁棒方案下SU消耗的功率小，鲁棒方案考虑了信道的扰动，消耗的功率虽然有所增加，却保证了各个SU的QoS需求。鲁棒功率分配算法中，SU满足认知系统总功率预算门限的要求，符合理论的分析，验证了鲁棒算法的可行性。

非鲁棒方案与鲁棒方案SINR的性能比较如图4所示。

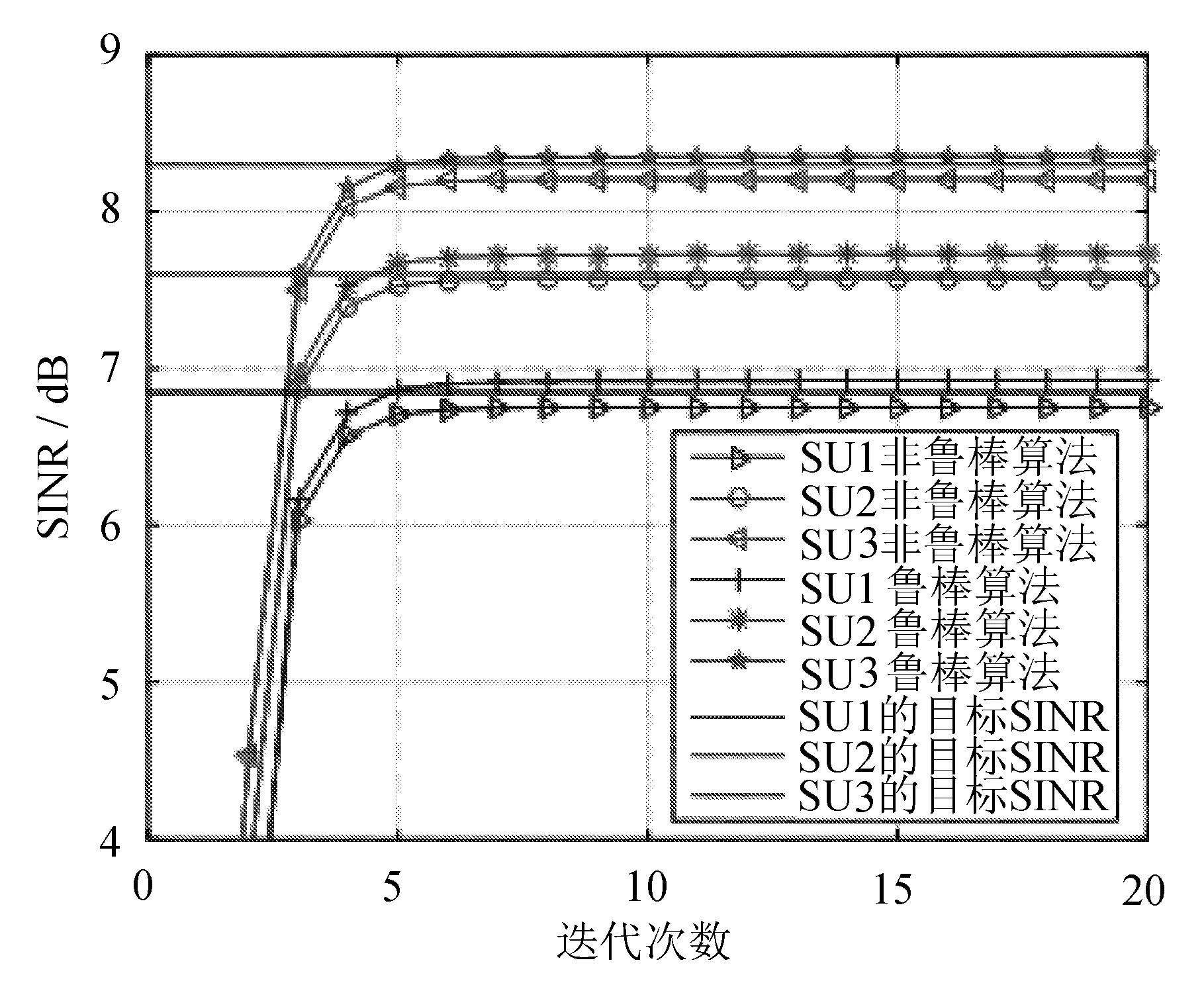
图4 两种方案下SINR的性能比较

从图4可以看出,鲁棒方案满足了对应用户的目标SINR，而非鲁棒方案却没能满足。虽然非鲁棒功率分配算法满足PU的干扰功率阈值约束，但是却不能实现SU满意的QoS。对于动态的认知无线电通信系统，非鲁棒方案显然是无能为力的。鲁棒方案在满足SINR需求的前提下，最小化SU的功耗，既保证了系统的无缝通信，又提高了系统的能量效率。

4 结 语

在Ad-Hoc认知无线电网络中，考虑了信道增益的扰动，提出了一种基于鲁棒的功率分配算法。仿真结果表明，该功率分配算法与非鲁棒算法相比，既能快速达到纳什均衡，又能保证各个SU的QoS需求，更加高速快捷地实现频谱资源共享。

[1] S Haykin. Cognitive radio: Brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.

[2] L Cao, H Zheng. Distributed rule-regulated spectrum sharing[J]. IEEE Journal on Selected Areas in Communications,2008,26(1):130-143.

[3] C H Pan, J Z Wang, W C Zhang. Power minimization in multi-band multi-antenna cognitive radio networks[J]. IEEE Transactions on Communications,2014,13(9):5056-5069.

[4] M H Islam, Y C Liang, A T Hoang. Distributed power and admission control for cognitive radio networks using antenna arrays[C]// Proc. IEEE DySPAN07, Dublin, Ireland：[s.n.],2007:250-253.

[5] S Lasaulce, Y Hayel, R El Azouzi, et al. Introducing hierarchy in energy games[J]. IEEE Transactions on Communications,2009,8(7):3833-3843.

[6] S Stotas, A Nallanthan. Enhancing the capacity of spectrum sharing cognitive radio networks[J]. IEEE Transactions on Vehicular Technology,2011,60(8):3768-3779.

[7] 黄镇.认知网络中非完美CSI下的鲁棒功率分配研究[D].长沙:中南大学,2013.

[8] S Boyd, L Vandenberghe. Convex optimization[M]. England: Cambridge University Press,2004:24-46.

[9] 王盼盼.基于信道增益不确定性的认知无线电网络鲁棒功率控制算法[D].秦皇岛:燕山大学,2014.

[9] 王宇飞.认知无线电资源分配鲁棒算法[J].长春工业大学学报，2015，36(5):515-518.

Robust power allocation algorithm for cognitive radio systems

ZHU Meng, WANG Hongzhi, ZHOU Mingyue*, BAI Yang

(School of Computer Science and Engineering, Changchun University of Technology, Changchun 130012， China)

Considering the interference power threshold from primary user (PU), overall transmission power budget for Secondary User (SU) and Signal to Interference Noise Ratio (SINR), we put forwards an energy-efficiency power allocation algorithm based on robustmultiuser cognitive radio networks. Lagrange algorithm is used to obtain the power allocation in the worst situation with the theory of convex optimization. Simulation results indicate that the algorithm is feasible.

cognitive radio; power allocation; robust optimization.

10.15923/j.cnki.cn22-1382/t.2017.1.08

2016-09-25

吉林省教育厅基金资助项目(2016343)

朱 孟(1991-)，男，汉族，安徽淮南人，长春工业大学硕士研究生，主要从事认知无线电功率分配方向研究,E-mail:zhumengvipzm@163.com. *通讯作者：周明月(1980-)，女，汉族，吉林长春人，长春工业大学讲师，博士，主要从事认知无线电系统中资源分配问题研究,E-mail:zmyjlu@ccut.edu.cn.

TN 929.5

A

1674-1374(2017)01-0043-05