岭回归和主成分回归下的农业总产值因素分析

董小刚, 赵 浪, 林诗明, 王纯杰

(长春工业大学 基础科学学院， 吉林 长春 130012)



岭回归和主成分回归下的农业总产值因素分析

董小刚, 赵 浪, 林诗明, 王纯杰

(长春工业大学 基础科学学院， 吉林 长春 130012)

选取7个影响吉林省农业总产值的因素,运用SAS软件建立了农业总产值的多元回归模型。为解决经典线性回归模型的多重共线性问题， 运用主成分回归模型和岭回归模型对其进行了修正,最后对这两个修正模型进行了比较分析,得出岭回归模型相对较优的结论。

SAS软件; 多重共线性; 主成分回归; 岭回归

0 引 言

吉林省地处中国东北中部地区,拥有辽阔的平原地带和富饶的水域环境等自然资源,素有“黑土地之乡”的美称,其人均耕地面积处于全国前列,是中国重要的粮食生产基地之一。无论是从地理位置还是从拥有的自然资源来看,吉林省都具有高效农业发展的优势,了解吉林省农业总产值的影响因素,提出有利于吉林省农业发展的政策建议,有效促进农业的发展,这对吉林省以及全国都有重要的影响。文中将通过建立多元线性回归模型分析影响吉林省农业总产值的影响因素。

1 影响因素的选取与数据的来源

很多因素影响农业总产值,哪些才是主要的影响因素,这又是一个复杂的问题。由于农业发展直接影响国民生活,因此影响农业产值因素的分析一直以来备受关注,梅玟[1]从时间序列分析的角度研究了政策因素对安徽省农业产值增长的制约;汤鹏主[2]采用协整分析方法,并基于VAR模型对变量建立脉冲响应函数和进行方差分解,对财政支农支出和农业产值两者的关系进行了研究;孙杨[3]通过线性回归的方式研究了农业机械化水平对农业总产值的影响;高雯[4]对农业总产值与化肥施用量、农用机械总动力、有效灌溉面积、成灾面积进行了回归分析;张溥[5]分析了中国农业产值影响因素并对影响因素与农业产值之间进行了多元回归分析;钟雅珊[6]通过多元对数计量经济模型研究了农业生产总值与农用机械总动力、第一产业就业人数、财政对农业的支出的关系。上述研究中,涉及对农业总产值的影响因素相当有限,难以看出这些因素综合起来对农业总产值的影响,文中将对被解释变量为农业总产值,解释变量为7个对农业总产值影响较大的因素进行多元回归分析。即:农业总产值Y为被解释变量,指从事农林牧渔业总产值[3-6];农业从业人员X1,指从事农林牧渔业的劳动者人数;农作物播种面积X2,指实际播种或移植有农作物的面积;有效灌溉面积X3,指具有一定水源配套设备的耕地面积;农业机械总动力X4,指主要用于农林牧渔业的各种动力总和;农村用电量X5,指农村范围内从事生产经营、日常生活用电总量;化肥使用量X6,指本年内实际用于农业生产的化肥数量;财政支农支出X7,指国家财政对农村各项生产的支出。文中影响因素指标和数据皆来源《吉林省统计年鉴2015》,数据分析均在SAS9.4环境中[7]实现。

2 多元线性回归模型分析

[8]

对农业总产值增长的研究方法多种多样,有采用柯布—道格拉斯生产函数模型[9],有采用脉冲响应函数方法来分析[10],也有基于灰色关联度分析[11];常见的是采用逐步回归分析的方法来分析[12-14]。文中分别采用了主成分回归和岭回归两种方法来对影响农业总产值因素进行分析，并对这两种方法进行比较分析。

首先,对被解释变量Y和各个解释变量Xi进行相关分析,从输出的结果可以看出,被解释变量与解释变量之间具有很大的相关性,除了Y和X1的相关系数为0.5左右,其余的都为0.9左右,其中Y与X4的相关系数甚至高达0.992;再通过绘制散点图，考察被解释变量Y随各解释变量Xi的变化情况。从被解释变量与各个解释变量的“散点图矩阵”也可以看出,除了解释变量X1外,被解释变量Y与其他的解释变量Xi均成线性趋势关系,说明可以考虑建立一个多元线性回归模型。再对各个解释变量间进行相关分析,从输出的相关系数矩阵可以看出,各相关系数对应的P值都很小,说明各个解释变量之间是显著相关的。

设被解释变量Y与解释变量X1,X2,…，X7的多元线性回归模型的一般形式为:

式中：β0,β1,β2,…,β7----未知参数；

β0----回归常数；

β1,β2,…,β7----回归系数；

ε----随机误差。

运用普通最小二乘估计的方法求得各个参数估计值。拟合出回归模型:

0.077 3X3+0.298 7X4+50.167 3X5+

由方差分析表可知,F统计量的值为1 051.99,所对应的P值<0.000 1,说明模型整体拟合得很好;复决定系数R2=0.996 2,调整后的R2=0.995 3,说明模型对样本的拟合效果很好。再由参数估计表知,解释变量X2,X3,X4,X6,X7的t检验统计量所对应的P值均>0.05,说明这些变量对被解释变量影响不显著。在上述分析中已知各个解释变量之间具有很大的相关性,则出现解释变量检验效果不显著可能是存在多重共线性的缘故。

共线性诊断见表1。

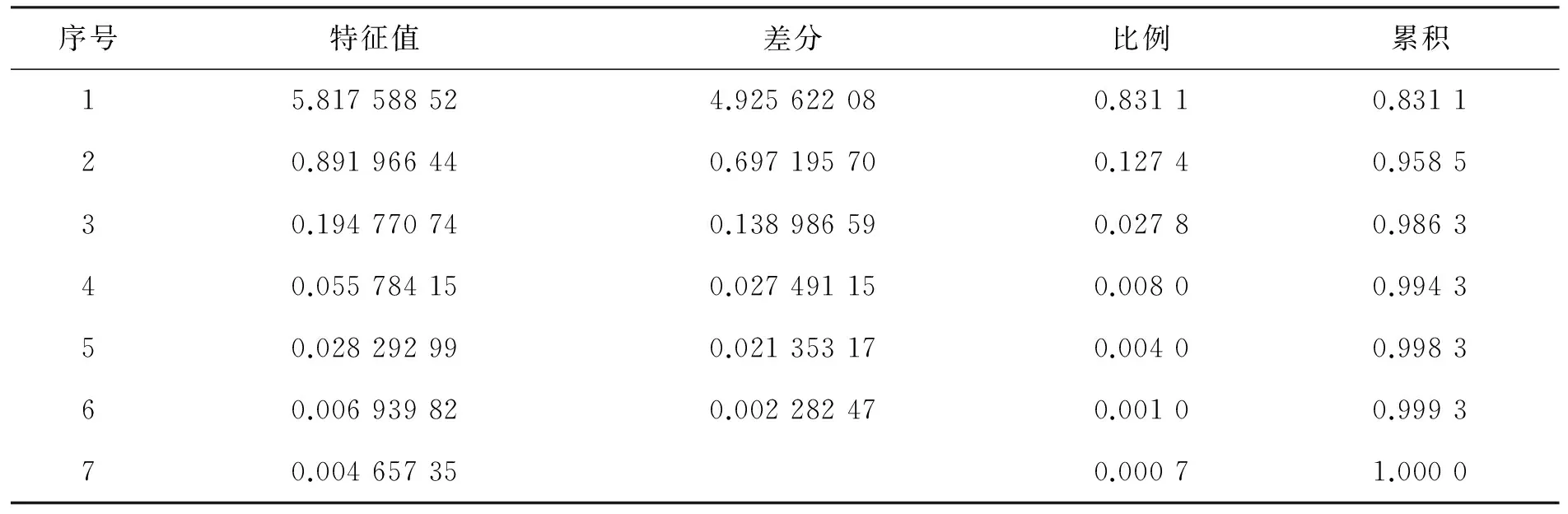
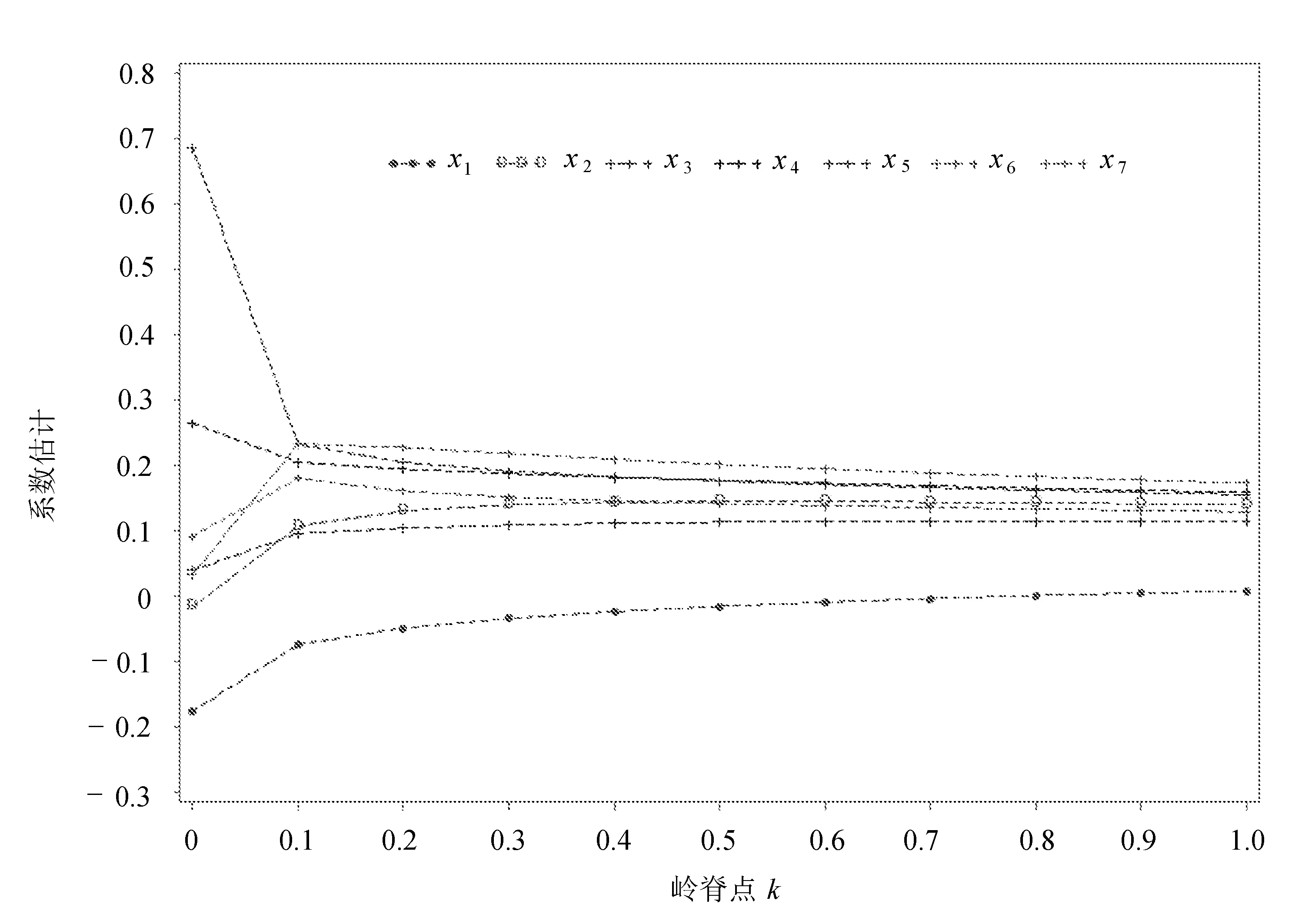
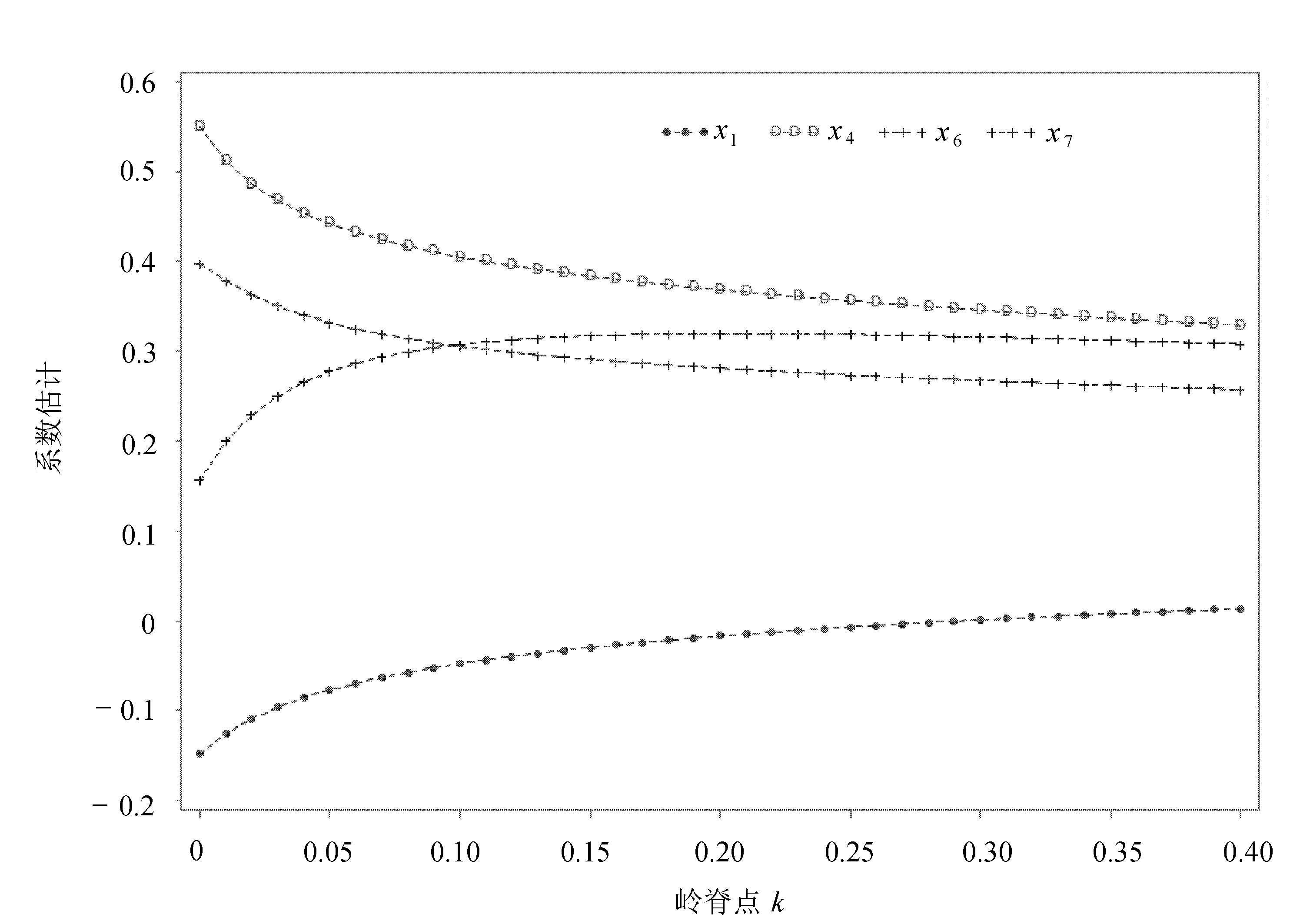
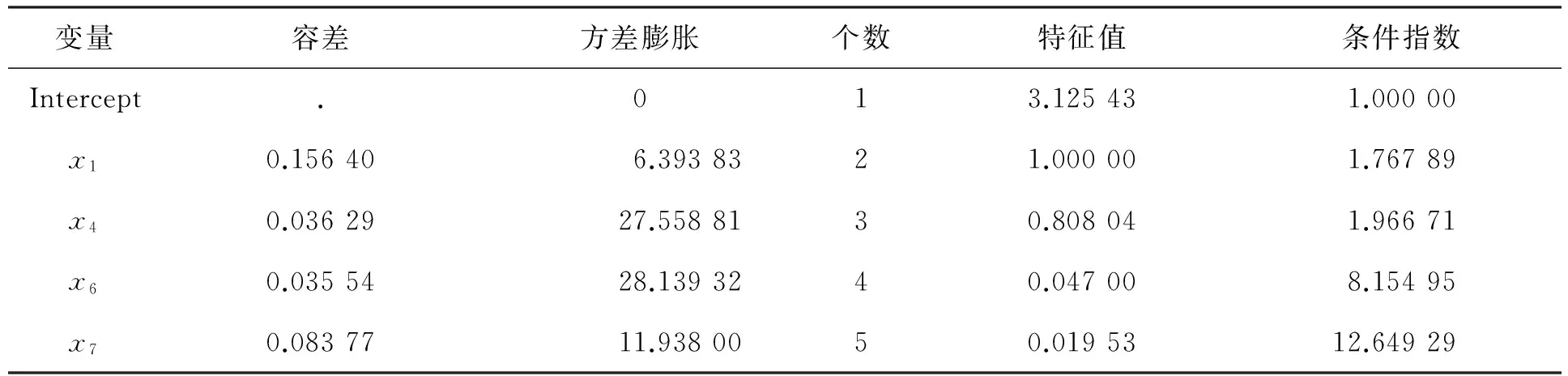
根据spearman相关系数表知样本等级相关系数rs的t检验统计量所对应的P值均>0.05,说明不存在异方差性;由Durbin-Watson D诊断表知DW=1.778,经查DW检验表知dL=0.877,dU=1.749,dU

表1 共线性诊断

3 主成分回归和岭回归分析

考虑到各个解释变量之间的单位不同,先把原始数据标准化,这样可以消除量纲对数据结构的影响。

3.1 主成分回归

主成分回归方法与普通最小二乘回归方法不同,当存在多重共线性关系时,主成分回归是以牺牲无偏性换取方差的大幅度减小,最终降低均方误差,达到回归估计最优的目的;主成分回归主要运用主成分分析里面降维思想,由于主成分分析是在不至于损失太多信息的情况下利用正交旋转变换把多个指标转化为几个综合指标,且各个综合指标之间互不相关,所以再用这些综合指标来进行回归分析就很好地消除了多重共线性带来的影响。

相关矩阵的特征值见表2。

表2 相关矩阵的特征值

表2中,最大的特征值为5.817 588 52,最小的是0.004 657 35。再看看累积贡献率,第一个主成分为83.11%,说明第一个主成分里面包含了原始数据里面的83.11%的信息量,前两个主成分的累积含有原始数据里面的95.85%的信息量。所以取两个主成分就足够。即:

Z1= 0.254 386STDX1+0.385 153STDX2+0.393 001STDX3+0.407 750STDX4+

Z2= 0.825 713STDX1-0.273 124STDX2+0.109 378STDX3-0.176 918STDX4-

再用Y对这两个主成分Z1,Z2作普通最小二乘回归,得到主成分回归方程为:

从方差分析表可以看出,F统计量的值为1 223.46,其P值<0.000 1,说明该模型整体拟合得很好;复决定系数R2=0.986 3,调整后的R2=0.985 5,说明这个模型对样本的拟合效果很好。再由参数估计表知,Z1,Z2的t检验统计量的P值均<0.01,即参数通过检验。综上所述,该主成分回归模型可行,该模型为:

将Z1,Z2代入上式即得标准化的主成分回归方程:

还原为原始数据的主成分回归方程为:

从模型(8)可知,X1每增加一个单位,Y就减少0.616 45个单位;X2每增加一个单位,Y就增加0.219 09个单位;X3每增加一个单位,Y就增加0.263 75个单位；X4每增加一个单位,Y就增加0.219 09个单位;X5每增加一个单位,Y就增加12.606 3个单位;X6每增加一个单位,Y就增加1.116 61个单位;X7每增加一个单位,Y就增加1.862 83个单位。说明农业总产值与农业从业人员(X1)表现出负相关的关系,农业总产值与其他影响因素都表现为正相关的关系,且在各个因素中,农村用电量(X5)对农业总产值的影响处于最大,化肥使用量(X6)和财政支农支出(X7)对农业总产值的影响也很大。农业总产值实际值与主成分回归拟合值的对比折线图如图1所示。

图1 农业总产值实际值与主成分回归拟合值的对比折线图

从图中可以看出,该模型拟合出来的值与实际值接近。

3.2 岭回归分析

岭回归(ridge regression)是对普通最小二乘估计的一种改进方法,由霍尔(A.E.Hoerl)在1962年首次提出来,1970年霍尔又和肯纳德(Kennard)对岭估计给予了详细讨论。当解释变量间存在多重共线性,|X′X|≈0时,如果把一个正常数矩阵kI(k>0)加到X′X中,则X′X+kI接近奇异的程度就会比X′X接近奇异的程度小很多,进而改进普通最小二乘估计,达到消除共线性影响的效果。用岭回归方法消除多重共线性的问题,其实就是一种解释变量选元过程。岭迹图如图2所示。

由图2可以看出,当k值较小时,X5的标准化岭回归系数的绝对值比较大,并且随着k的增大而迅速减小,根据原则二[8]将X5剔除;X3的标准化岭回归系数相对稳定并且系数的绝对值比较小,则根据原则一[8]可将其剔除;同样,可将变量X2剔除。再对剩余的变量X1,X4,X6,X7重新作岭回归分析,岭迹图如图3所示。

图2 岭迹图

图3 重岭回归岭迹图

从图3可以看出,岭回归模型的岭参数k处于0.20～0.30时,岭参数基本处于稳定状态,因此取岭参数k=0.25,此时Y对X1,X4,X6,X7标准化后岭回归方程为:

由方差分析表可知,F统计量的值为1 115.07,所对应的P值<0.000 1,说明岭回归模型整体拟合效果很好;复决定系数R2=0.992 9,调整后的R2=0.992 0,说明此模型对已知样本的拟合效果非常好。再由参数估计表知,X1,X4,X6,X7的t检验统计量的P值均<0.01,即参数通过检验。综上所述,此岭回归模型可行。再对模型进行多重共线性检验,见表3。

表3 共线性诊断

由表3可知，最大方差膨胀值和最大条件指数分别为28.139 32和12.649 29,这比普通最小二乘回归下的最大方差膨胀值(145.814 65)和最大条件指数(139.486 75)有了很大的减少,说明岭回归模型在很大程度上消除了多重共线性的影响。

由模型(9)可知,X1每增加一个单位,Y就减少0.007 02个单位;X4每增加一个单位,Y就增加0.356 02个单位;X6每增加一个单位,Y就增加0.273 53个单位;X7每增加一个单位,Y就增加0.318 85个单位。说明农业总产值Y和农业从业人员(X1)存在着负相关关系,农业机械总动力(X4)、化肥使用量(X6)、财政支农支出(X7)为影响农业总产值Y的主要因素。农业总产值实际值与岭回归拟合值的对比折线图如图4所示。

图4 农业总产值实际值与岭回归拟合值的对比折线图

从图中可以看出,该模型拟合出来的值与实际值接近。

3.3 模型对比分析

在上述分析中,分别运用了主成分回归法和岭回归法来消除多重共线性的影响,最终得出两个模型,见表4。

表4 解释变量选择准则

从模型检验和参数检验来看,各个检验统计量的P值均<0.01,说明模型与参数均通过检验;从C(p)准则来看,2.000 0<4.000 0,说明主成分回归模型相对较优;从R2准则来看,0.986 3<0.992 9,说明岭回归模型相对较优;从AIC准则来看,-151.455 1>-171.012 0,说明岭回归模型相对较优。并且岭回归的变量解释更加符合实际,综上分析,岭回归模型相对较优,即:

因此,影响农业总产值Y的主要因素有农业机械总动力(X4)、化肥使用量(X6)、财政支农支出(X7)。而农业总产值Y受农业从业人员因素(X1)的影响很小,并且农业总产值Y和农业从业人员因素(X1)表现出负相关的关系。

4 结论与建议

4.1 农业劳动力投入

从模型(10)可以看出,农业总产值和农业从业人员存在着负相关的关系,且系数绝对值较小,反映出劳动力过剩、利用效率低下的状况。进入21世纪以来,科技快速发展,农业机械化水平越来越高,逐渐取代了手工劳动,农业从业人员的增加不再是拉动农业产值的重要途径。为了解决这一问题,政府应该拓宽农村从业人员的工作渠道,转移一定量的农业劳动力到其他产业,并对继续从事农业的劳动力进行培训教育,使其掌握先进的技术来提高农业产出。

4.2 农业机械总动力

从模型(10)可以看出,农业总产值和农业机械总动力存在着正相关的关系,且系数绝对值最大,表明了农用机械总动力对农业总产值有着最大的影响,农业机械化是现代农业科技水平的表现,也是农业产值增加的关键。因此,吉林省政府应该加大对大型拖拉机、收割机、农药喷洒机等大型机械设备的投入,来大幅度提高农业生产率和生产力水平。

4.3 财政支农支出

从模型(10)可以看出,农业总产值和财政支农支出存在着正相关的关系,且系数的绝对值第二大,表明财政支农支出对农业总产值起着至关重要的影响,增加农业财政支出力度会引起农业总产值的增加。因此,吉林省政府应该加大对农业的财政倾斜力度,保持对农业补贴的持续、稳定增长,并对吉林省财政支农支出的结构进行调整,对财政支农支出资金的管理体制进行完善。同时,积极引导社会力量投资于农业的生产、技术开发、新品种推广，以弥补国家财政的不足。

4.4 化肥使用量

从模型(10)可以看出,农业总产值和化肥的使用量存在着正相关的关系,且系数的绝对值第三大,表明化肥使用量对农业总产值的影响较大,增加化肥的投入量会引起农业产值的增加。但在实际中,我们不仅不能大规模的增加化肥的投入量,反而应该对其采取谨慎的态度,合理施用。过量施肥会增加不必要的成本,降低了农作物的产出,更为严重的是导致了土地盐碱化、土壤肥力的下降,不利于农业的可持续发展。因此,化肥的使用必须合理,在保证农产品需要的基础上,对化肥实行有效配置,对氮磷钾合理配置,提高化肥的利用率,保证农业总产值的稳定增长。

[1] 梅玟.安徽省农业产值增长制约因素的相关分析[J].技术经济,2006,25(7):84-86.

[2] 汤鹏主.财政支农支出和农业产值增长的关系[J].现代经济探讨,2008(8):71-75.

[3] 孙杨.农业总产值影响因素的分析:以机械总动力为影响因子[J].内蒙古科技与经济,2008(11):2-3.

[4] 高雯.我国“两型”农业发展影响因素分析[J].安徽农业科学,2011,39(27):17049-17051.

[5] 张溥.中国农业产值影响因素分析[J].商场现代化,2013(5):106-107.

[6] 钟雅珊.农业总产值的影响因素综合分析[J].经济研究,2013(29):56-60.

[7] 夏坤庄.深入解析SAS[M].北京：机械工业出版社,2015:442-469.

[8] 何晓群.应用回归分析[M].4版.北京:中国人民大学出版社,2015:57-203.

[9] 漆文萍.农业总产值指数影响因素的模型分析:以江西省为例[J].南昌大学学报,2005,36(4):67-72.

[10] 李国璋.我国农业产值的影响因素分析[J].统计与决策,2007(22):83-85.

[11] 徐静.吉林省农业产业结构的灰色关联度分析[J].企业导报,2013(23):159-160.

[12] 迪娜·帕夏尔汗.影响新疆农林牧渔产值增长因素的逐步回归分析法:基于1979-2013年时间序列数据[J].新疆农业科技,2015(3):1-3.

[13] 吕海燕.基于逐步回归分析的河南粮食产量因素研究[J].河南科学,2013,31(12):2133-2136.

[14] 王纯杰，董小刚，陈嘉，等.基于分位数回归的长春市职工工资水平的分析[J].长春工业大学学报：自然科学版,2010,31(4):367-373.

Agriculture output factor analysis with ridge regression and principal component regression

DONG Xiaogang, ZHAO Lang, LIN Shiming, WANG Chunjie

(School of Basic Sciences, Changchun University of Technology, Changchun 130012， China)

Seven factors influencing agricultural output of Jilin Province are selected and then the multiple regression model for the output is established with SAS software. To solve the multicollinearity problem in the classical linear regression model, we adjust the model with both the principal component regression and ridge regression model. The improved the models are compared and it comes to a conclusion that the ridge regression has better performance.

SAS software; multicollinearity; principal component regression; ridge regression.

10.15923/j.cnki.cn22-1382/t.2017.1.01

2016-10-17

国家自然科学基金资助项目(11301037,11571051); 吉林省教育厅“十三五”规划项目(2016317)

董小刚(1961-)，男，汉族，吉林长春人，长春工业大学教授，博士，主要从事数理统计方向研究,E-mail:dongxiaogang@ccut.edu.cn.

C 812

A

1674-1374(2017)01-0001-07