径向固定瓦滑动轴承动特性计算及分析

洪红伦，宋晓明，韩彦龙，马永凯，谷 巍

(1.承德石油高等专科学校 机械工程系，河北 承德 067000；2.中海石油(中国)有限公司 湛江分公司，广东 湛江 524000)



径向固定瓦滑动轴承动特性计算及分析

洪红伦1，宋晓明1，韩彦龙1，马永凯2，谷 巍1

(1.承德石油高等专科学校 机械工程系，河北 承德 067000；2.中海石油(中国)有限公司 湛江分公司，广东 湛江 524000)

以径向固定瓦滑动轴承为研究对象，研究载荷和转速对轴承动特性的影响。针对上述目的建立径向固定瓦滑动轴承的数学模型，并基于有限元法对相关方程进行数值求解。通过该方法获得了载荷和转速对径向固定瓦滑动轴承动特性影响的相关规律：动特性系数基本上随转速增加而有所减小，随比压增加而增加，但也因方向的不同导致其变化的幅值出现较大差异。

有限元；固定瓦轴承；数学模型；动特性

随着我国工业的迅速发展，滑动轴承已广泛应用于石油化工、机械制造以及钢铁冶炼等众多行业的生产设备中，并且往往是这些设备能否安全可靠运行的关键[1]。该类轴承性能计算的理论为流体动力润滑[2,3]，流体动压油膜具有润滑性能，同时也具有动力学性能，对于轴承-转子系统的振动有很大影响[4,5]。通常将油膜等效为线性的弹簧和阻尼器，用弹簧的刚度系数和阻尼器的阻尼系数来描述油膜的动特性，即动特性系数[6]。笔者建立以雷诺方程为核心的数学模型，并利用有限元数值解法求解相关方程，研究载荷和转速对滑动轴承动特性的影响，相关规律可为同行业的工作者提供参考。

1 数学模型及数值求解

1.1 数学模型的建立

1.1.1 雷诺方程

计算轴承特性时，一般先由雷诺方程解出压力分布，然后积分获得相关性能。本文假设轴承定常工况下运转，且具有等温膜油润滑，考虑润滑油的紊流效应，则相应雷诺方程为公式(1)。

(1)

式中：U为轴颈的表面切向速度；p为油膜压力；h为油膜厚度；μ为润滑油的动力黏度；kx、kz为流态系数。

1.1.2 膜厚方程

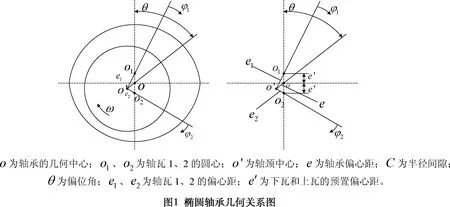
对于椭圆轴承(如图1所示)，需分别表达下瓦1和上瓦2的膜厚，表达下瓦h1时，从连心线OjO1远离h1 min的一端作为φ1角的原点，则由椭圆轴承的几何关系可得到下瓦和上瓦的膜厚为：

(2)

式中：

由此，下瓦和上瓦的最小膜厚分别为：

h1min=C-e1

h2min=C-e2

(3)

轴承性能求解中，两膜厚的较小值即为最小膜厚。

1.2 数值求解

1.2.1 方程求解

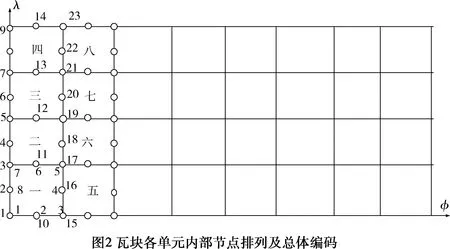
本文轴承性能计算采用有限元法进行。轴瓦关于轴向中分面对称，故兼顾计算效率与准确度，仅求解轴瓦的一半即可。网格划分如图2所示，瓦块包角150°的范围共划分网格数为(20×8)个，其中20为周向网格数，8为轴向网格数(取一半进行求解时轴向划分为4个)。

1.2.2 动特性计算

在轴心在静平衡位置附近作微小运动时，油膜力的增量可由下列线性关系表达：

(4)

式中：

则轴承的动力特性系数可表达如下：

(5)

2 轴承结构介绍

以某椭圆轴承为例，研究载荷和转速对径向固定瓦滑动轴承动特性的影响。该轴承额定转速为3 000r·min-1，轴承直径480mm，轴承宽度为300mm，其他结构参数见表1。对于滑动轴承而言，一般用比压表征轴承的载荷，所以研究载荷对动特性的影响分析就是研究比压对动特性的影响。本文分别计算了比压为2.0MPa、2.4MPa、2.8MPa、3.0MPa、3.3MPa和3.5MPa的轴承的动特性。

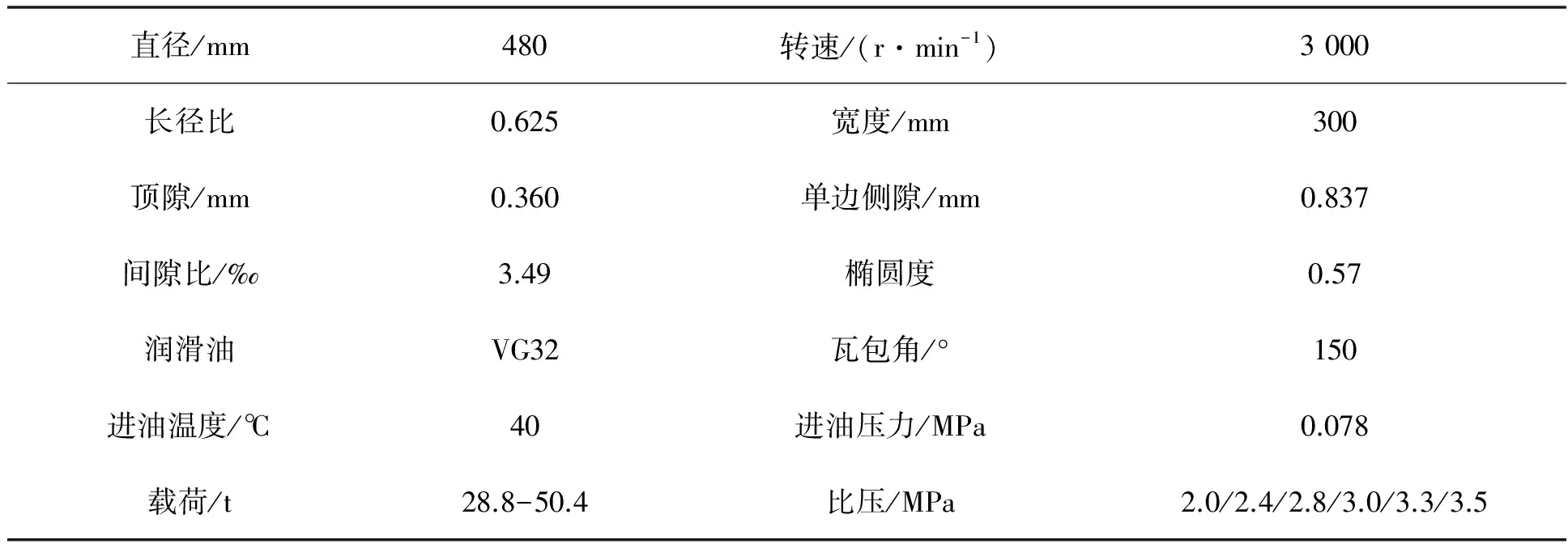
表1 椭圆轴承参数

3 动特性分析

针对表2中的椭圆轴承，计算多种比压下的动特性，绘制相关曲线。图3为不同比压下刚度随转速变化曲线。从图3(a)～图3(d)可以看出动特性中的四个刚度系数随比压的增大而增大。转速由1 000 r·min-1增加至3 500 r·min-1，水平主刚度Kxx出现波动，但基本数值变化不大；垂直主刚度Kyy、交叉刚度Kxy和交叉刚度Kyx三个动特性系数在不同比压下则随转速的增大而呈现减小现象。

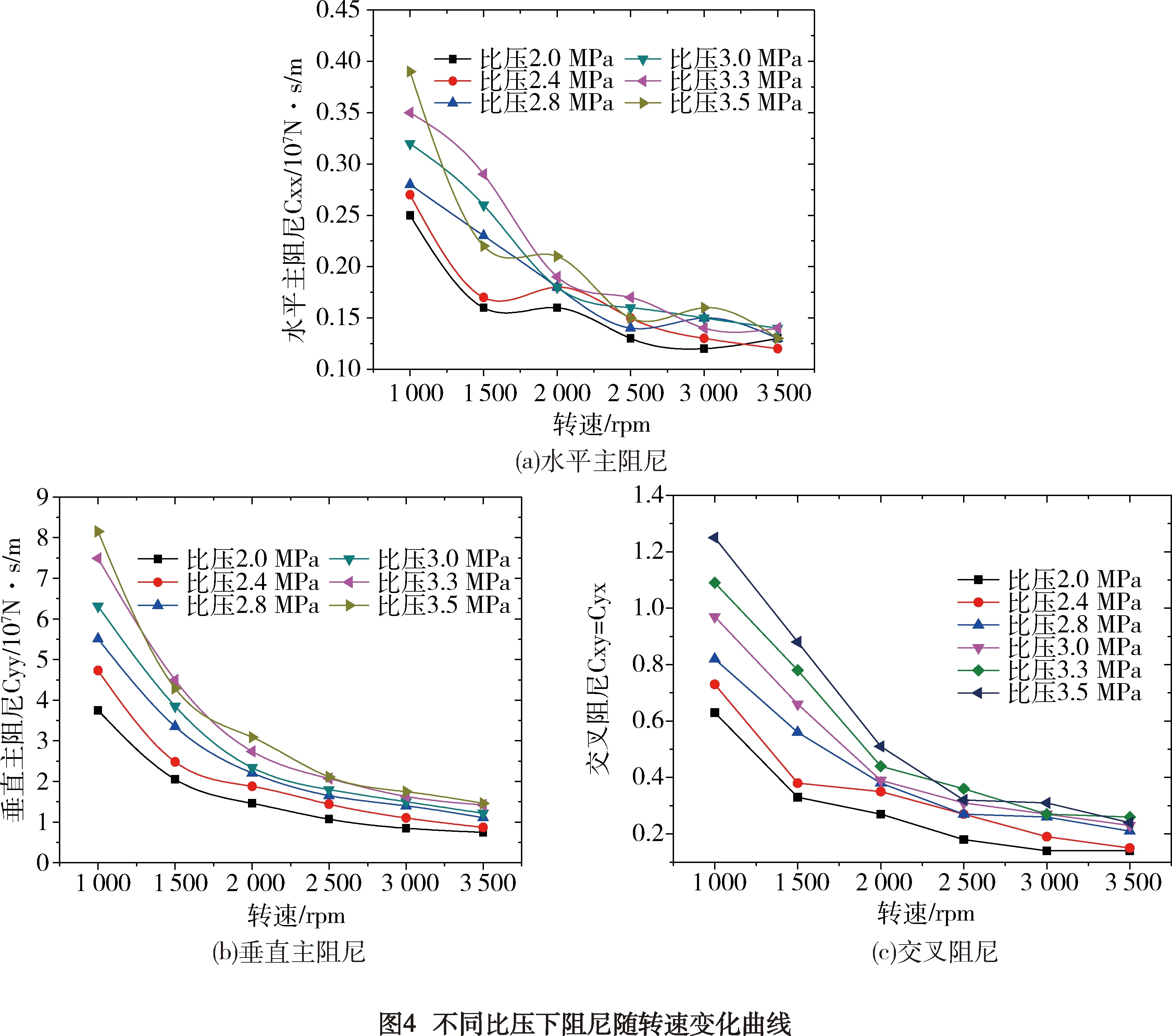
图4为不同比压下阻尼随转速的变化曲线。从图4(a)～图4(c)可以看出动特性中的四个阻尼系数随比压的增大而增大。转速由1 000 r·min-1增加至3 500 r·min-1，阻尼系数在不同比压下随转速的增大而呈现减小现象。同时，两个交叉阻尼项Cxy和交叉刚度Cyx相等。

由图3和图4看出，随转速增加，各比压下的轴承主刚度和主阻尼均有所减小，且垂直主刚度和垂直主阻尼下降幅度远大于水平主刚度和水平主阻尼。图5为额定转速下主刚度和主阻尼随比压变化规律图。图5显示比压增加时，轴承的垂直主刚度和垂直主阻尼大幅增加，水平主刚度和水平主阻尼变化不大。额定转速3 000 r·min-1下，比压由2.0 MPa增加到3.5 MPa时，垂直主刚度增加162%，水平方向主阻尼增加100%。

4 结论

本文建立以雷诺方程为核心的数学模型，并基于有限元法对相关方程进行数值求解，为研究载荷和转速对滑动轴承动特性的影响建立理论基础。总体上看，不同比压下，随转速增加轴承主刚度和主阻尼均有所减小,且垂直主刚度和垂直主阻尼下降幅度远大于水平主刚度和水平主阻尼。比压增加时，轴承的垂直主刚度和垂直主阻尼大幅增加，水平主刚度和水平主阻尼变化不大。此外，两个交叉刚度均随比压的增大而增大，随转速的增大而减小，并且二者不相等；两个交叉阻尼项则完全相等，受比压和转速的影响规律与交叉刚度类似。

[1] O Pinkus and B Sterlicht.流体动力润滑理论[M].西安交通大学轴承研究组译.北京：机械工业出版社，1980.

[2] 孙大成．润滑力学讲义[M]．北京：中国友谊出版公司，1985．

[3] 朱均.流体润滑滑动轴承技术的研究动态[J].润滑和密封,1993,95(1):62-68.

[4] Zavyalov OG, Alyabyeva YV, Savchenkova OS. Effect of the lubricating layer on rotor stability in sliding bearings[J].Journal of Friction and Wear, 2009,30(4):235-241.

[5] 闻邦椿,武新华,丁千，等.故障旋转机械非线性动力学的理论与试验[M].北京:科学出版社,2004.

[6] 史冬岩,张成,任龙龙,等.滑动轴承压力分布及动特性系数[J].哈尔滨工程大学学报,2011(9):1134-1139.

Calculation and Analysis of Dynamic Characteristics of Radial Fixed Bearing

HONG Hong-lun1, SONG Xiao-ming1, HAN Yan-long1, MA Yong-kai2, GU Wei1

(1.Department of Mechanical Engineering, Chengde Petroleum College, Chengde 067000, Hebei, China; 2.Zhanjiang Branch of CNOOC Limited, Zhanjiang 524000, Guangdong, China)

In this paper, the influence of load and speed on the dynamic characteristics of the radial fixed bearing is studied. The mathematical model of the radial fixed bearing is established. Based on the finite element method, the relevant equations of the mathematical model are solved by numerical method. Thus we obtain the relevant rules of dynamic characteristics: dynamic coefficient basically decreases with speed increasing, increases with load increasing. However amplitude of the change is also a large difference because of the different direction.

finite element; fixed bearing; mathematical model; dynamic characteristics

2016-09-03

洪红伦(1990-)，男，河北保定人，助教，硕士，主要研究滑动轴承、转子动力学,E-mail:1043295785@qq.com。

TH133.3

A

1008-9446(2017)01-0036-05