区域似大地水准面精化的方法探讨与精度分析
布金伟,左小清
(昆明理工大学 国土资源工程学院,云南 昆明 650093)
区域似大地水准面精化的方法探讨与精度分析
布金伟,左小清
(昆明理工大学 国土资源工程学院,云南 昆明 650093)
阐述与GPS/水准高程拟合相关的基本理论及区域似大地水准面精化的原理与方法,并结合区域的具体实例,重点比较二次多项式曲面拟合法、三角剖分双线性内插法、加权平均推估法的精度情况,从中得到结论。实验表明,在没有足够重力数据的支持下,三角剖分双线性内插法获得比较理想的精度,利用该方法精化似大地水准面获得的高程可以代替四等水准。
GPS/水准;区域似大地水准面;二次多项式曲面拟合法;三角剖分双线性内插法;加权平均推估法
随着全球导航卫星(GNSS)定位技术及连续运行参考站(CORS)的广泛应用,能提供高于10-7相对精度的大地测量数据,但我国使用的高程系统是正常高系统,GNSS 获得的数据高程为大地高。如果地区没有一个高精度高分辨率似大地水准面模型,即使能用GNSS给出高精度的大地高,也无法达到GPS大地高至正常高的高精度转换[1-2]。为了满足用GPS代替水准测量方法测定高程的需求,似大地水准面需要达到厘米级精度。而在地形起伏复杂的某些区域,还存在一定的缺陷,因此本文从理论上利用不同类型的观测数据,从算法上对似大地水准面进行精度分析。
1 几种拟合方法的原理
1.1 多项式曲面拟合法
曲面拟合[3-6]是一种局部逼近的方法。基本思想是以每一个内插点为中心,用内插点周围数据点的值建立一个拟合曲面,使其到各数据点的距离加权平方和为极小,而这个曲面在内插点上的值就是所求内插值。
根据地区高程变化的复杂程度,可选n次曲面来拟合,设高程控制点的高程异常值ζ与坐标(x,y)之间的函数关系式为
ζ(x,y)=a0+a1x+a2y+a3xy+
a4x2+a4y2+….
(1)
各高程异常点的已知高程异常与其拟合值之差为
Δi=ζ(x,y)-ζ(x,y).
(2)
Δi称为残差。根据最小二乘原理,应有
(3)
原则下,求出式中各系数ai,那么就可以利用相应的拟合方程推算出其它点的高程异常值。对函数式求一阶偏导,则
(4)
求二阶偏导
(5)
一旦拟合函数确定(确认拟合次数),ai(i=1,2…)均为一常数,模型函数与某一切平面存在一个切点,说明几何表示为一抛物单曲面,仅有一个凹面或图面。
上述的多项式曲面拟合存在以下问题:拟合多项式阶次过高,则拟合曲面形态过于复杂;拟合多项式阶次过低,GPS/水准点使用率太低,其携带的高精度信息体现不显示;残差模型不通过GPS/水准点,容易出现异常点;且拟合面边缘地区会出现剧烈的震荡现象。考虑到山区地形起伏大,似大地水准面变化复杂。由此,论文提出进一步分区拟合的思想,采用三角剖分双线性内插法与加权平均推估法进行拟合。
1.2 小三角形双线性内插法
1.2.1 Delaunay准则三角形剖分
三角剖分是将离散的残差点剖分成不规则的三角形网,Delaunay三角剖分满足以下两个准则:①空圆准则,网中任一三角形的外接圆范围内不会有其它点存在;②最大化最小角准则,其所形成的三角形的最小角最大。采用Delaunay准则进行三角剖分具有如下特点[7]:①以最临近的三点形成三角形,且各线段皆不相交,可保证拟合成果具有高空间相关性;②剖分结果唯一性;③任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么两个三角形6个内角中最小角不会变大,避免内插时出现病态方程;④改变任意节点只会影响相邻三角形,保证误差不会整网传递。
1.2.2 双线性内插法的原理
设三角形的3个端点分别为A,B,C,点L、点R分别位于AB与AC上,待求点P为直线LR上的点,又由于三点决定一面,即点P在此面上,而通过P点的二维直线段在此面上有无数条,又因为无论任何一条从理论上内插出的点值是唯一的,故为方便计算,设上述点P,L,R中Y值相同,即YP=YL=YR。则点P,点R,点L的内插高程异常差值算式为
(6)
1.3 加权平均推估法
关于推估问题,主要有两种方法:一种是以最小二乘推估法为代表的统计推估方法;另一种是函数拟合法、加权平均法等为主的解析推估方法。由于前者的计算工作量大,本论文采用加权平均法推估内插点处的高程异常差值。
假设三角形为ABC,待求点为P, 则算式为
(7)
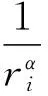
2 残差模型的建立
在没有足够重力数据的条件下,构想利用地区局部区域高精度GPS/水准高程异常控制网与省级精化似大地水准面叠加融合,利用局部高精度高分辨率纠正广域低精度低分辨率,实现建立局部区域厘米级精度似大地水准面模型。
首先将GPS/水准获得的高程异常值[8]与省级精化似大地水准面计算的高程异常值求差,获得残差值。
Δξ=ξGPS-ξG,
(8)
ξGPS=H水准-H大地高,
(9)
ξG=H插值-H大地高.
(10)
综合以上算式得到简化算式为
Δξ=H水准-H插值.
(11)
式中:Δξ为两种基准高程异常值差值;ξGPS为GPS/水准获得的高程异常值;ξG为省级精化似大地水准面计算的高程异常值。
利用离散的残差值采用几何方法构造一个连续的拟合数值模型
Δξ=f(B,L).
(12)
式中:B,L为坐标系与椭球参数统一的纬度与经度。
在连续的残差数值模型上叠加融合省级精化似大地水准面计算的高程异常值ξG,即采用移去-恢复法完成区域似大地水准面的构建。
ξ′(B,L)=Δξ(B,L)+ΔξG(B,L).
(13)
该方法避免了缺少重力数据而丢失物理场信息的弊端,以及纯几何拟合内插的缺陷,可靠性和精度更高。
3 算例分析
3.1 项目说明
整个项目共有4个分区,论文采用一分区作为实验区域,测区范围为98.625 km2。其中,已有测区周围GPS的C级点2个,GPS的D级点16个,坐标系为×××市坐标系,测区内有1985国家高程基准的一等水准点1个,二等水准点18个,同时有***局提供的三等水准点成果。
基于连续运行参考站(CORS)同步快速静态观测模式进行GPS一级控制测量,完成GPSⅠ级控制点35个;利用四等水准测量对GPS一级点进行高程联测,完成四等水准观测88.5 km。其中,35个一级GPS点转换至2000国家坐标系后,参与插值软件计算,高程异常差值见表1,残差统计结果见图1。

表1 高程异常差值表 m
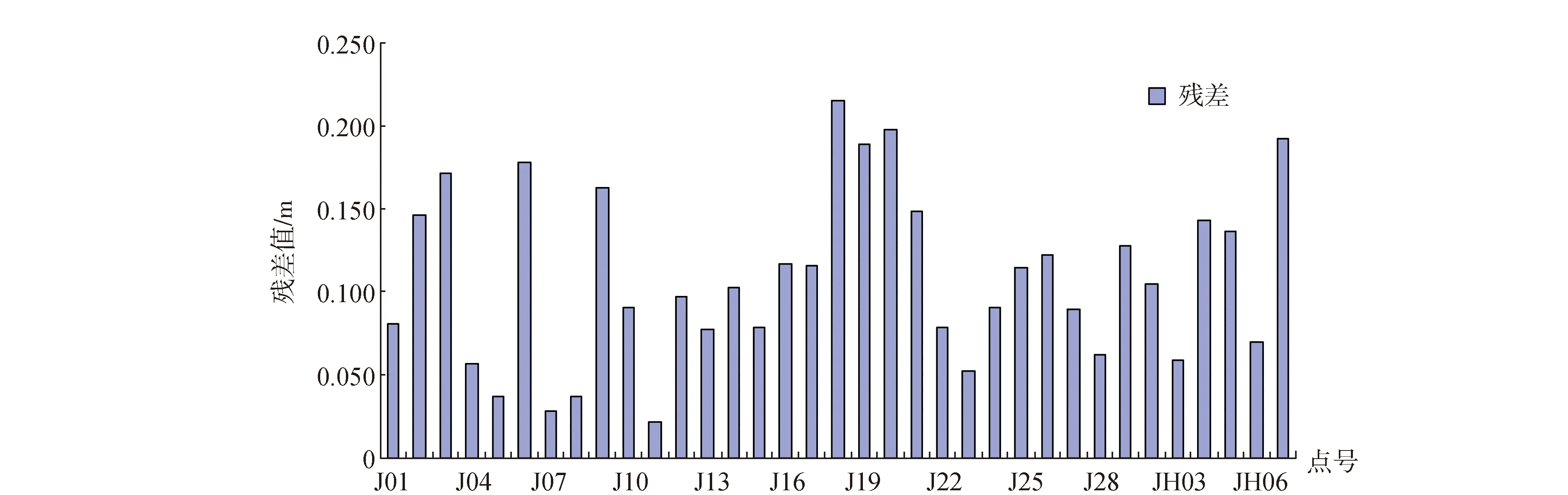
图1 残差统计
3.2 残差模型算法分析
残差模型法的关键在于寻求数学算法,确定f(B,L),使其能准确反映区域GPS/水准与省级精化似大地水准面之间的差距。
3.2.1 多项式曲面拟合法
按二次计算,则高程异常差值算式为
Δξ(x,y)=a0+a1x+a2y+a3xy+a4x2+a5y2.
(14)
其中,35个一级GPS点全部参与拟合计算,最终内符合精度统计见表2。

表2 多项式曲面拟合残差表 m
根据统计计算,高程异常差值拟合残差中误差:MΔξ=0.028 5 m。
3.2.2 三角剖分双线性内插法与加权平均推估法
3.2.2.1 Delaunay准则三角形剖分
根据试验区35个GPS/水准点以及计算的相应的省级精化似大地水准面高,选择27个点参与计算,其余8个分布均匀的点用于外部检核。以这27个残差点为节点,采用Delaunay准则将整个测区剖分成小的三角形区域,整个测区的三角剖分结果见图2。

图2 Delaunay三角剖分示意图
3.2.2.2 三角剖分双线性内插
在对高程异常差值点进行三角剖分后,要对待求点所在小三角形进行拟合计算,计算采用双线性内插法。然后,根据式(12)将ξG省级精化似大地水准面与残差拟合模型叠加,建立区域精化似大地水准面ξ′(B,L)。则拟合叠加以后计算的正常高高程为
H′=H+ξ′(B,L).
(15)
通过计算,检核点的拟合、叠加计算高程与实际GPS/水准高程对比数据见表3。
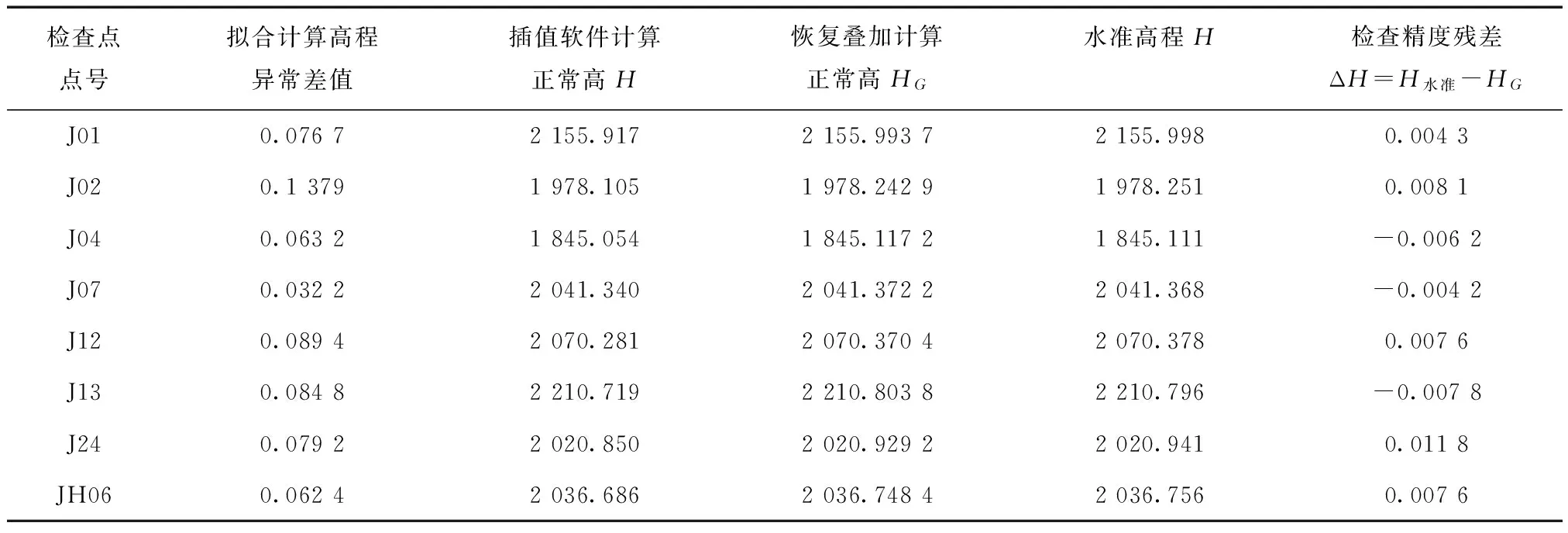
表3 双线性内插法精度检查统计表 m
根据表3分析统计,建立的区域似大地水准面基于水准数据的检核中误差为:

3.2.2.3 加权平均推估

选择27个点参与计算,其余8个分布均匀的点用于外部检核。

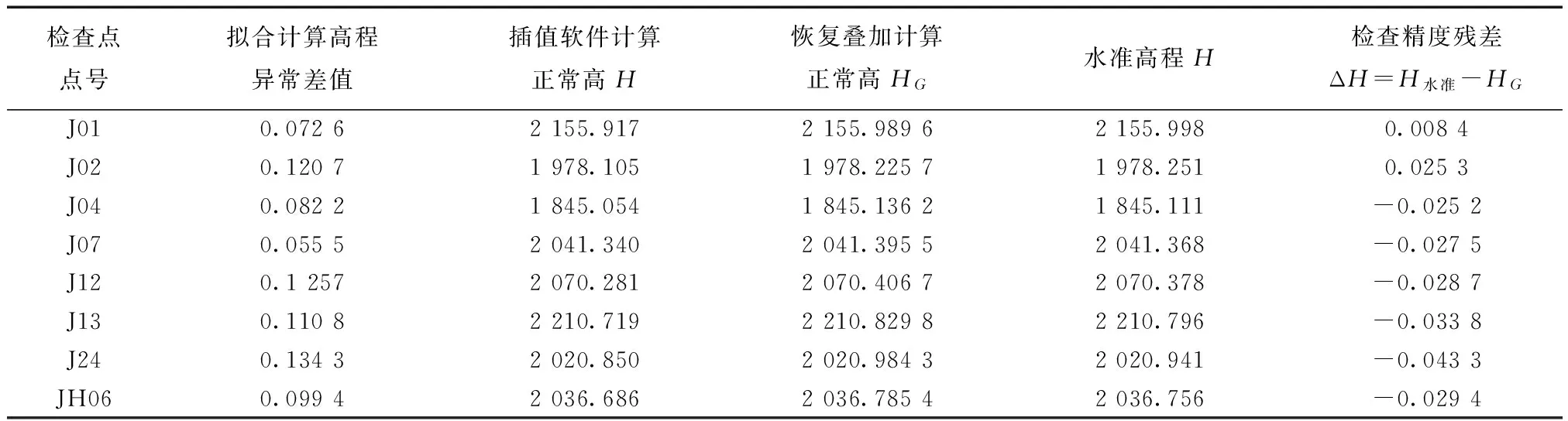
表4 加权平均推估法精度检查统计表 m


表5 加权平均推估法精度检查统计表 m


表6 加权平均推估法精度检查统计表 m
3.3 精度对比分析
由表7和图3分析可知:三角剖分双线性内插法和加权平均推估法明显比二次曲面拟合法效果更为理想,精度相对更高。主要原因有两点:①由于二次曲面拟合为整体区域拟合,可能由于似大地水准面变化不平缓引起拟合函数无法准确表达,而三角剖分则使得拟合区域分成若干小的三角形拟合区域,拟合精度分配较为均匀;②二次曲面拟合是不过点拟合,拟合后的曲面不经过已知高程异常控制点,而三角剖分双线性内插法和加权平均推估法是以各个已知高程异常控制点为顶点进行内插,保证过点拟合的优势。


表7 二次曲面拟合法、三角剖分双线性内插法和加权平均推估法精度对比表 m
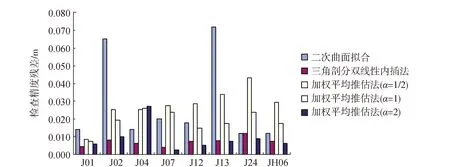
图3 二次曲面拟合法、三角剖分双线性内插法和加权平均推估法精度对比图
4 结 论
从实验数据分析得出的精度,可得如下结论:
1)在没有足够重力数据的支持下,三角剖分双线性内插法获得了比较理想的精度,利用该方法精化似大地水准面获得的高程可以代替四等水准。

[1] 魏立峰.城市似大地水准面精化成果的应用[J].地理空间信息,2016,14(7):57-58.
[2] 郭春喜,聂建亮.区域似大地水准面拟合方法及适用性分析[J].大地测量与地球动力学,2013,33(1):103-107.
[3] 朱毅.云南省局部区域似大地水准面精化方法探讨与精度分析[D].昆明:昆明理工大学,2012.
[4] 高西峰.GPS水准在带状区域似大地水准面精化中的应用研究[D].西安:长安大学,2007.
[5] 王绍地.区域大地水准面精化理论与应用研究[D].西安:长安大学,2013.
[6] 黄鹏.市级大地水准面精化的研究与应用[D].青岛:山东科技大学,2010.
[7] 刘振宇,高炳浩.基于CQG2000的吉林省西部地区似大地水准面的建立[J].测绘学报,2010,39(5):441-443,464.
[8] 范占永,李磊.GPS似大地水准面精化及精度分析[J].水利与建筑工程学报,2015,39(5):161-164.
[责任编辑:张德福]
Discussion of quasi local level method and its precision analysis
BU Jinwei, ZUO Xiaoqing
(School of Land and Resources Engineering, Kunming University of Science and Technology, Kunming 650093,China)
This paper presents the principle and method of GPS/ leveling fitting the basic theory and the regional quasi geoid. Combined with concrete examples of regional key comparison, two polynomial curve fitting methods: bilinear interpolation method of triangulation, and weighted average push accuracy estimate method are given to obtain some useful conclusions. The experimental result shows that in the absence of sufficient gravity data, triangulation bilinear interpolation can obtain the ideal accuracy,by which the method of refined quasi geoid height can cover the fourth level.
GPS/ level; quasi local level; two degree polynomial surface fitting method; bilinear interpolation method; weighted average method
引用著录:布金伟,左小清.区域似大地水准面精化的方法探讨与精度分析[J].测绘工程,2017,26(6):40-45.
10.19349/j.cnki.issn1006-7949.2017.06.008
2016-07-15
布金伟(1992-),男,硕士研究生.
P228
A
1006-7949(2017)06-0040-06

