一种加快BDS精密单点定位初始化的方法

杨克凡，柴洪洲，潘宗鹏

(信息工程大学，河南 郑州 450001)

一种加快BDS精密单点定位初始化的方法

杨克凡，柴洪洲，潘宗鹏

(信息工程大学，河南 郑州 450001)

由于BDS卫星的星座特性及卫星的轨道和钟差的精度影响，使得传统消电离层组合精密单点定位(PPP)的初始化时间较长。针对上述问题，文中对附加电离层约束的非组合精密单点定位算法进行研究。首先介绍非组合PPP算法，分析其与传统PPP的差异；其次分别利用CODE电离层格网产品，以反距离加权算法计算的站星电离层延迟、低阶球谐函数建立的区域电离层产品等作为先验信息对非组合PPP进行约束。通过MGEX观测网实测数据静态和仿动态计算表明，相比传统消电离层组合PPP，附加电离层约束的非组合PPP能够有效缩短初始化时间，同时能够获得高精度的定位结果。

精密单点定位；区域电离层模型；先验信息；电离层约束；快速收敛

随着我国北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)的逐步完善和发展，基于BDS的PPP技术吸引了国内外学者的广泛关注。我国BDS自2012年底向亚太地区提供服务以来，国内外相关科研人员对BDS以及其它GNSS组合定位性能开展较为丰富的研究，得到许多有价值的理论。PPP作为一种有效便捷的高精度定位技术在测绘领域有着不可估量的前景，但由于BDS系统的卫星的星座特性及卫星的轨道和钟差的精度影响，使其收敛时间较长，限制PPP在实时、准实时领域的应用[1]。因此，如何针对北斗系统多星座和三频特点，提高北斗系统 PPP 的收敛速度，对于扩大PPP应用范围，扩展北斗应用领域，具有重要的理论研究价值和实际应用价值。

一般来说，PPP的首次收敛时间需要几十分钟甚至更长的时间。张小红等利用MGEX观测网数据对BDS与GPS收敛时间进行对比分析，得出无论静态还是动态，BDS都比GPS收敛时间长50 min左右的结果[1]。郝明等通过筛选最适合参数解算的初值，提出利用选权拟合的方法缩短PPP解算的收敛时间[2-3]。丁文武等针对卫星信号中断等原因导致的实时PPP重新初始化问题，设计了电离层延迟变化预报模型，并提出预报信息定权方法，实现PPP快速重新初始化[4]。林晓静等研究不同纬度地区的收敛速度，结果表明，纬度越高收敛越慢[5]。Garrett通过恒星日滤波法去掉多路径误差提高伪距精度，来加快精密单点定位的收敛[6]。

以上方法大多是基于传统的消电离层组合精密单点定位算法来进行PPP快速收敛的研究。然而，传统PPP算法在消电离层组合过程中不但舍弃了部分观测信息，而且观测噪声放大近3倍，不利于位置参数的快速收敛[7～9]。针对此问题，本文采用基于原始观测数据的非组合精密单点定位算法，该算法能够有效避免传统精密单点定位消电离层组合过程中观测噪声的放大。

文献[10]研究表明，采用非组合观测量理论上与消电离层组合PPP(Ionosphere-free Combination PPP, IF-PPP)等价，能够获得一致的最终定位结果。但采用非组合观测量，将电离层延迟当成参数进行估计[11～12]，不仅能够获得相应的电离层延迟产品，同时能够充分利用先验的电离层延迟信息，作为先验约束，增强方程的强度，使得缩短精密单点定位的初始化时间成为可能。因此，本文采用非组合精密单点定位算法对BDS PPP的快速初始化进行研究。

1 精密单点定位模型及数据处理策略

1.1 观测方程

非组合精密单点定位(Uncombined Precise Point Positioning, UC-PPP)是一种基于单台接收机的双频非差原始观测数据，利用IGS等机构发布的精密卫星轨道和钟差产品确定全球任一点位置、接收机钟差、天顶对流层湿延迟及测站至卫星视线方向电离层延迟的方法[13]。忽略电离层高阶项，接收机r对卫星s第i频点的非组合观测方程为

(1)

(2)

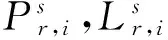
传统的消电离层组合精密单点定位算法(Ionosphere-free Combination PPP, IF-PPP)采用双频伪距和载波的无电离层组合来消除电离层延迟一阶项，消电离层组合观测方程可表示为

(3)

(4)

由上述两种算法的观测方程可知，两者均含有位置参数、接收机钟差参数、对流层湿延迟参数和模糊度参数，且模糊度参数中均含有伪距和相位硬件延迟偏差，失去整数特性，通常采用实数解。不同的是非组合PPP中含有电离层延迟项，并且把接收机端伪距硬件延迟作为参数进行估计。但是由于电离层参数与卫星端硬件延迟偏差线性相关，不能直接分离，为此本文利用先验的电离层延迟信息，引入一个电离层虚拟观测方程，作为先验约束。其虚拟观测方程为

(5)

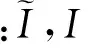
1.2 电离层先验信息

本文中的电离层先验信息除了采用CODE发布的GIM格网产品外，还采用反距离加权算法计算相应监测站非组合PPP估计的电离层参数，以及利用球谐函数建立的区域电离层模型产品。

1.2.1 反距离加权算法

首先利用非组合PPP算法解算出待估测站周围监测站相应卫星的电离层延迟信息，然后根据窗口法挑选出距离适宜的若干个监测站(见图1)，再采用反距离加权算法计算待估测站的电离层延迟信息作为先验信息。

反距离加权算法的数学表达式为

(6)

式中：I,Ii分别为待估测站和监测站的电离层延迟信息；di为相应监测站到待估测站的距离；n为窗口内监测站总数目。

图1 窗口法示意图

1.2.2 球谐函数建模

首先利用低阶球谐函数模型建立局域的电离层延迟模型，然后计算相应穿刺点的天顶方向电子总量(Vertical Total Electron Content, VTEC)值，再利用单层投影函数计算相应频点的电离层斜延迟。本文采用3阶的球谐函数模型，其数学表达为

(anmcosms+bnmsinms).

(7)

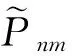
1.3 数据处理策略与参数估计

BDS PPP对于未知参数和各项误差项的处理方式与GPS PPP类似。在数据预处理过程中需要剔除存在明显错误的伪距观测值、观测值类型不完整以及数据历元个数较少的弧段，并综合采用MW组合法和电离层残差法进行周跳探测和粗差剔除。

非差数据载波相位周跳的修复比探测更加困难，某些周跳组合难以确定具体发生周跳的频率[14]，而且周跳修复结果受码伪距观测质量影响较大，修复正确率不高。因此，采取只探测不修复的策略，只要任意频点上探测到周跳，则认为两个频点上均发生周跳并同时做好标记，以便在解算过程中初始化模糊度参数。在定位解算的过程中还需对相对论效应误差、相位缠绕误差、天线相位中心偏差等影响在厘米级以上的系统误差进行模型改正，改正模型可参考文献[3]。

本文采用静态和仿动态定位模式，使用GFZ提供的精密星历和钟差产品来固定卫星轨道和钟差。由于卫星端DCB能保持较高的平稳性，且MGEX已发布高精度的GPS/BDS卫星端各频点的DCB产品。为减小数据处理复杂度，本文在数据预处理过程中先对单频伪距观测值进行卫星端DCB改正，在滤波过程中直接估计得到斜向电离层延迟和接收机端DCB参数。此外，由于观测量的精度与观测信号有关，在观测时，高度角较低的卫星信号受大气延迟和噪声影响高于高度角大的卫星，因此本文采用三角函数模型来计算不同高度角的卫星观测量精度。

同时，本文分别采用消电离层组合精密单点定位(Ionosphere-free Combination PPP, IF-PPP)，非组合PPP+电离层约束(Ionospheric Constrained PPP, IC-PPP)，两种模式下进行PPP定位解算。其中，为分析先验信息精度对IC-PPP定位解算性能的影响，电离层约束的先验信息分别采用CODE的GIM格网产品(GIM Ionosphere, GIMI), 区域建模产品(Area Model Ionosphere, AMI), 非组合PPP电离层反距离加权产品(PPP Estimates Ionosphere, PEI)来进行IC-PPP的解算，分别记为IC-GIMI-PPP, IC-AMI-PPP, IC-PEI-PPP。

本文采用扩展卡尔曼滤波(EKF)进行参数估计，具体的参数处理策略如表1所示。

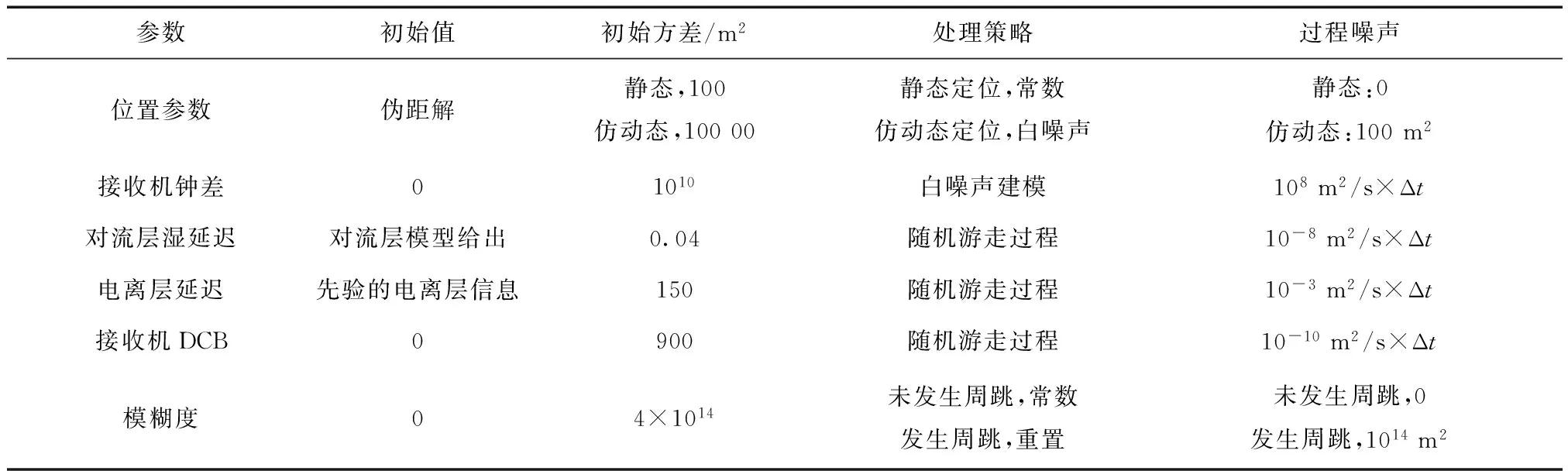
表1 滤波初始条件与参数处理策略

2 试验与分析

2.1 试验数据

由于北斗系统星座特点和全球监测站分布的限制，试验数据选取15个中国地壳运动观测网监测站2015年DOY 055-057共计3 d的观测数据，进行区域电离层建模，并用相应时段内的MGEX观测网JFNG站的观测数据作为实验对象，数据采样间隔为30 s，截止高度角10°。本文所采用数据监测站位置分布如图2所示。

图2 测站位置分布

实验将每个测站24 h观测数据切割，按每3 h重新初始化，共计8个收敛弧段。将各弧段的PPP解算结果与GFZ网平差结果作差，以统计分析GPS/BDS PPP的收敛速度和定位精度。

2.2 实验结果及分析

本文中的收敛条件为定位偏差小于10 cm，且其后连续5 min定位偏差不超过10 cm。首先以DOY 055 JFNG站第一时段的定位结果为例，比较分析GPS/BDS PPP的定位偏差序列。

2.2.1 静态PPP收敛分析

图3、图4给出JFNG站GPS/BDS水平方向和高程方向静态的定位偏差序列。 从图中可以看出，在静态精密单点定位的收敛阶段，GPS IF-PPP的收敛速度和GPS IC-PPP的收敛速度相当，收敛时间均约为25 min；而BDS IC-PPP的收敛速度要快于BDS IF-PPP的收敛速度，前者收敛时间约为65 min，后者约为70 min。这主要是由于BDS异构星座中的GEO卫星基本保持不变，造成BDS卫星几何结构变化缓慢，同时BDS的精密星历和精密钟差精度要低于GPS，造成两种系统不同的收敛效果。此外，由于使用先验的电离层信息作为约束，增加BDS冗余观测量，增强方程的强度，使得BDS IC-PPP的收敛速度相对于BDS IF-PPP有一定的提高。但由于GPS精密星历和精密钟差精度较高，卫星几何结构变化较快，方程强度较稳定，解算的位置参数精度较高，因此定位变化不如BDS明显。

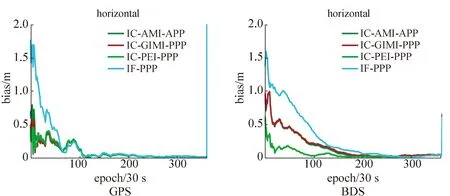
图3 DOY 055 JFNG站GPS/BDS水平方向静态定位结果

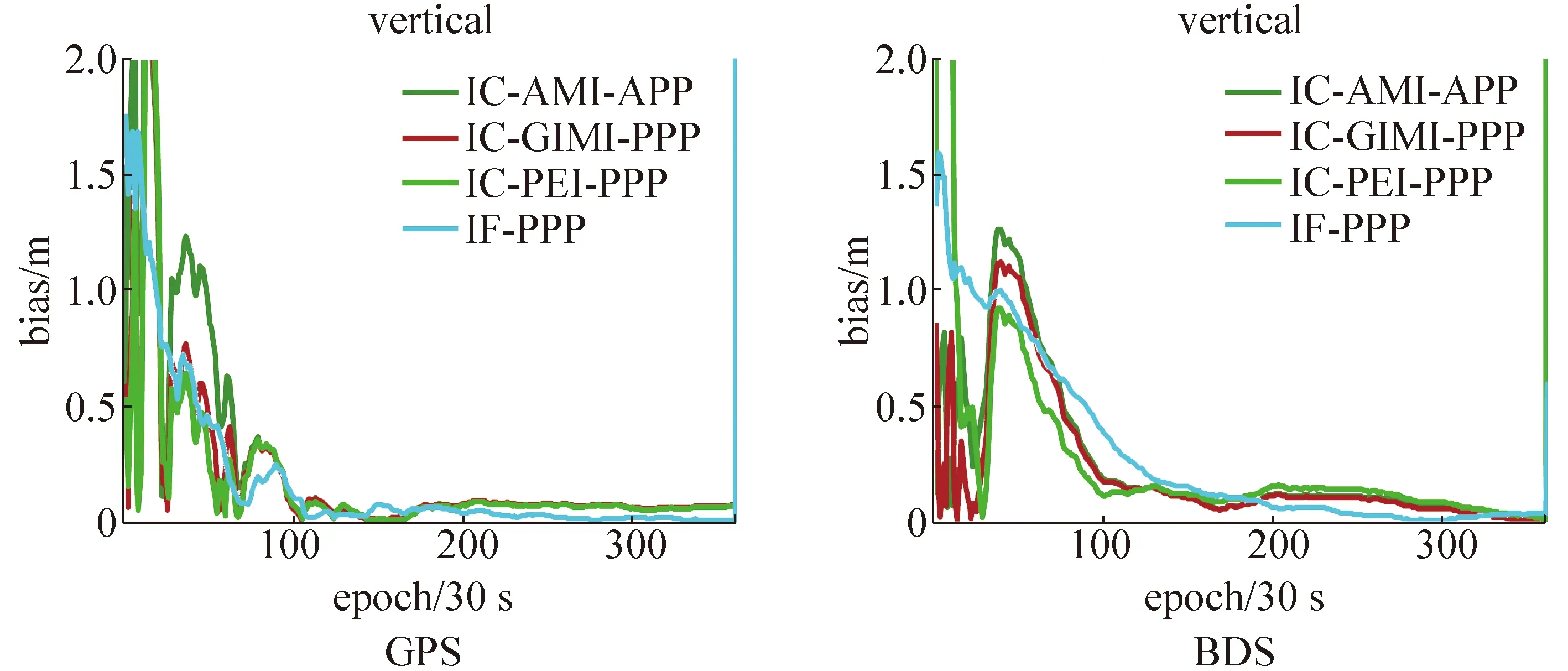
图4 DOY 055 JFNG站GPS/BDS高程方向静态定位结果

同时，对于附加电离层先验信息约束的IC-PPP 3种方案来说，GPS的收敛速度没有明显的区别，收敛速度基本相当；而对于BDS系统，水平方向IC-PEI-PPP的收敛速度明显要快于另外两种，高程方向三者基本相同，同时IC-GIM-PPP与IC-AMI-PPP的收敛速度相当。这是由于距离较近的监测站与待估测站时空相关性较强，计算得到的电离层信息精度较高，使得IC-PEI-PPP收敛速度要快于IC-GIM-PPP与IC-AMI-PPP的收敛速度。

图5给出静态PPP 8个收敛时段相同观测时间的三维定位偏差RMS值。从图中可以看出，相对于传统的消电离层组合PPP算法，附加电离层约束的非组合PPP算法的收敛速度得到明显的提高。

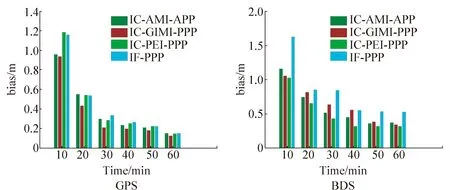
图5 DOY 055 JFNG站GPS/BDS静态PPP相同观测时间收敛对比

2.2.2 动态PPP收敛分析

图6、图7给出JFNG站GPS/BDS水平方向和高程方向仿动态的定位偏差序列。 从图中可以看出，在仿动态精密单点定位水平方向的收敛阶段，GPS IF-PPP的收敛速度和GPS IC-PPP的收敛速度趋于一致，收敛时间约为45 min；而BDS IC-PEI-PPP的收敛速度与BDS AMI-PPP在水平方向的收敛速度基本相当，均快于IC-GIM-PPP与IC-IF-PPP的收敛速度，前两者的收敛时间约为70 min，后两者的收敛时间约为85 min，这可能是由于PEI和AMI产品的精度要高于GIM产品的精度造成的结果。在高程方向，GPS 4种PPP方案的收敛时间基本相同；而对于BDS，IC-PEI-PPP在50 min时达到收敛精度，其余3种方案在70 min时达到收敛精度。

图6 DOY 055 JFNG站GPS/BDS水平方向仿动态定位结果

图8给出仿动态PPP 8个收敛时段相同观测时间的三维定位偏差RMS值。从图中可以看出，相同观测时间内IC-PEI-PPP与IC-AMI-PPP的收敛精度最高，IC-GIM-PPP的收敛精度次之，IF-PPP的收敛精度最低。这主要是由于在中国区域的IGS观测站较少，计算的GIM格网产品精度与中国区域电离层模型精度相比较低，说明电离层先验信息的精度越高，对非组合PPP的收敛速度提高的越大。此外，相对于传统的消电离层组合PPP算法，短时间动态条件下，不考虑时空相关性，附加电离层先验信息的非组合PPP算法能够提高PPP的收敛速度，获得较高精度的定位结果。

2.2.3 平均收敛时间分析

为进一步分析附加电离层先验信息约束的非组合PPP算法对收敛速度的影响，统计分析了DOY 055～077计3 d的平均收敛时间，收敛条件为三维定位偏差小于10 cm，且后续5 min定位偏差不超过10 cm，统计结果如表2所示。

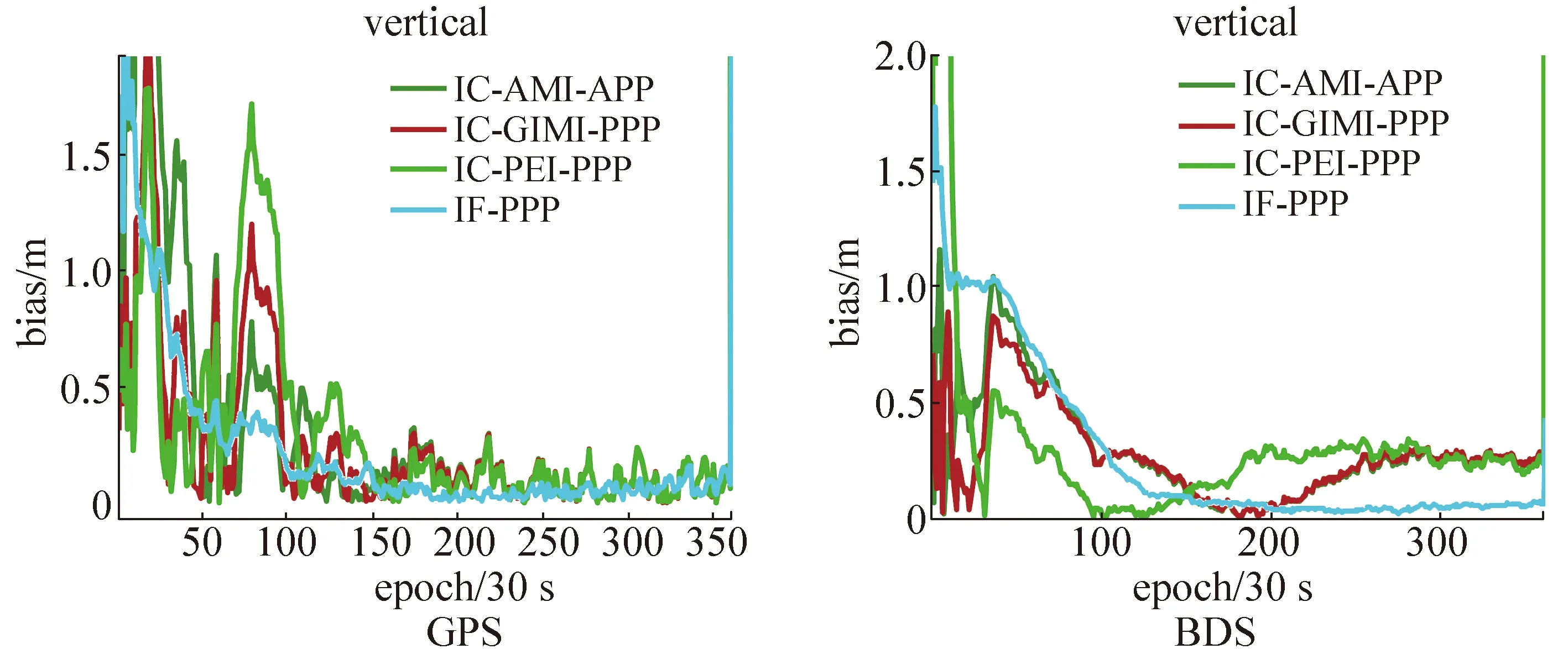
图7 DOY 055 JFNG站GPS/BDS高程方向仿动态定位结果

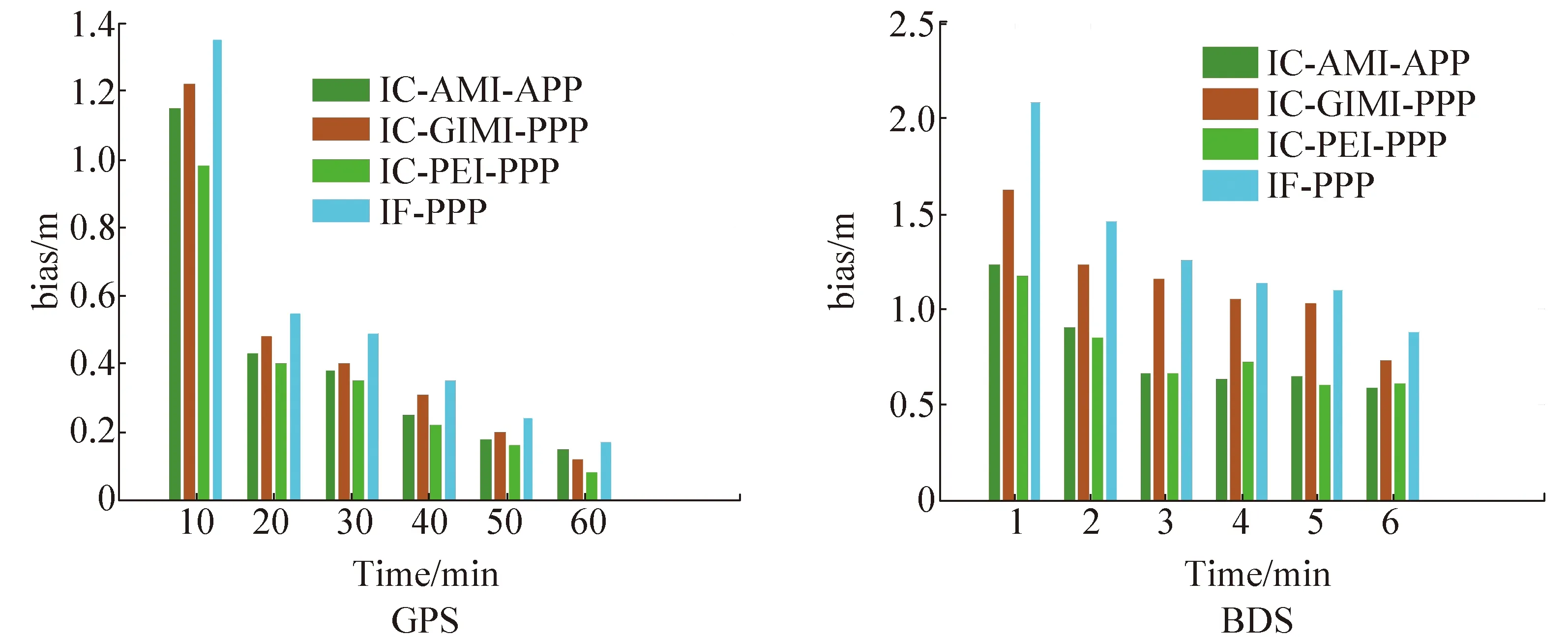
图8 DOY 055 JFNG站GPS/BDS动态PPP相同观测时间收敛对比

表2 DOY 055～077静态/仿动态平均收敛时间 min

从表2可以看出，对于GPS/BDS静态和仿动态PPP，3种附加电离层先验信息约束的非组合PPP收敛时间均低于传统消电离层组合PPP，同时GPS IC-PPP与IF-PPP平均收敛时间的差异要小于BDS。此外在仿动态条件下，IC-PEI-PPP与IC-AMI-PPP的平均收敛时间要低于IC-GIM-PPP的平均收敛时间。这也说明，相对于消电离层组合PPP算法，附加电离层约束的非组合PPP算法能够增加冗余观测量，增强方程的强度，加快PPP的收敛速度，且先验的电离层信息精度越高，收敛速度提高的越快。但BDS PPP收敛速度提高要高于GPS，这主要是由于BDS卫星几何结构变化缓慢，精密星历和精密钟差精度较低造成的。

3 结 论

针对BDS消电离层组合PPP初始化时间较长的问题，本文采用附加电离层延迟约束的非组合PPP算法，将电离层斜向延迟作为参数进行估计，来进行BDS PPP的快速初始化研究，并分析不同精度的电离层先验信息对非组合PPP收敛速度的影响。实验结果表明：在短时间观测条件下，附加电离层延迟约束的非组合PPP的收敛速度要明显快于传统的消电离层组合PPP，但是对于GPS收敛速度的提高没有BDS显著。同时，在局域范围内，反距离加权算法计算得到的电离层先验信息对于BDS非组合PPP的收敛速度提高的最大，可考虑用反距离加权算法计算电离层延迟信息，并播发给用户，以便提高其PPP收敛速度。

[1] 张小红，左翔，李盼，等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J].测绘学报，2015,44(3):250-256.

[2] 郝明，欧吉坤，郭建峰，等.一种加速精密单点定位收敛速度的因素分析[J].武汉大学学报(信息科学版)，2007,32(10):902-905.

[3] 李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉：武汉大学，2013.

[4] 丁文武. 附件电离层延迟约束的实时动态PPP快速重新初始化方法[J]. 地球物理学报， 2014 ，57(6)：1720-1731.

[5] 林晓静，张小红，郭斐，等.影响精密单点定位收敛速度的因素分析[J].测绘信息与工程，2010(3):10-12.

[6] SEEPERSAD G, BISNATH S. Reduction of PPP convergence period through pseudorange multipath and noise mitigation [J]. GPS Solutions, 2015, 19(3):369-379.

[7] 张宝成，欧吉坤，袁运斌，等. 基于GPS双频原始观测值的精密单点定位算法及应用[J].测绘学报，2010，39(5):478-483.

[8] LI X, GE M, ZHANG H, et al. A method for improving uncalibrated phase delay estimation and ambiguity-fixingin real-time precise point positioning[J]. Journal of Geodesy, 2013,87(5):405-416.

[9] 张小红, 左翔, 李盼. 非组合与组合PPP模型比较及定位性能分析[J]. 武汉大学学报(信息科学版)，2013，38(5):561-565.

[10] 张宝成.GNSS非差非组合精密单点定位的理论方法与应用研究[D].北京：中国科学院，2012.

[11] 张宝成，欧吉坤，袁运斌，等.利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J].测绘学报，2011,40(4):447-453.

[12] 张宝成，欧吉坤，李子申，等. 利用精密单点定位求解电离层延迟[J].地球物理学报，2011,54(4):950-957.

[13] 闫伟.GNSS系统仿真及精密单点定位研究与应用[D].北京：中国科学院，2012.

[14] 王爱生.数据质量控制理论及在GPS数据处理中的应用[D].北京：中国科学院测量与地球物理研究所，2009.

[责任编辑：张德福]

An accelerated initialization method of BDS precise point positioning

YANG Kefan, CHAI Hongzhou, PAN Zongpeng

(Information Engineering University, Zhengzhou 450001, China)

Due to the constellation characteristic of BDS satellite and the influence of satellite orbit and clock error, the traditional ionosphere-free combination precision point positioning (IF-PPP) tends to be longer. As for the problem, the uncombined precise point positioning (UC-PPP) algorithm with additional ionosphere constraints is studied. Firstly, the UC-PPP algorithm is introduced and then the difference between the UC-PPP and the IF-PPP is analyzed. Furthermore, the UC-PPP is constrained with the CODE global ionospheric map (GIM) updated every two hours, and with a regional satellite-specific correction model and a regional ionospheric model established by the low order spherical harmonic function. Finally, the MGEX data calculation shows that, compared to the IF-PPP, the UC-PPP with additional ionospheric constraint can effectively shorten the initialization time and obtain high accuracy of positioning result.

precision point positioning; regional ionospheric model; priori information; ionospheric constraint; rapid convergence

引用著录：杨克凡，柴洪洲，潘宗鹏.一种加快BDS精密单点定位初始化的方法[J].测绘工程，2017，26(6)：18-23，29.

10.19349/j.cnki.issn1006-7949.2017.06.004

2016-07-15

国家自然科学基金资助项目(41274045；41574010；41604013)

杨克凡(1989-)，男，硕士研究生.

P228

A

1006-7949(2017)06-0018-06