Henstock积分Newton-Leibniz公式的简捷证明
李伟
(集美大学理学院, 福建 厦门 361021)
宋述刚
(长江大学信息与数学学院,湖北 荆州 434023)
Henstock积分Newton-Leibniz公式的简捷证明
李伟
(集美大学理学院, 福建 厦门 361021)
宋述刚
(长江大学信息与数学学院,湖北 荆州 434023)
Newton-Leibniz公式是微积分学基本定理的一个重要应用,其建立了定积分与被积函数的原函数之间的联系,使得计算定积分问题从求和式的极限转化为求被积函数的原函数值差的问题。在Riemann积分、Lebesgue积分、Newton积分和δ(x)精细分划的基础上,建立了Henstock积分有关的基本概念,简述了Henstock引理及其证明,由此给出Henstock积分中的Newton-Leibniz公式,并给予简捷证明。
Riemann积分;δ(x)精细分划;Henstock积分;连续函数
Riemann积分[1](简称R-积分)建立之后,1902年在测度论[2]的基础上又建立了Lebesgue积分[3](简称L-积分)。L-积分推广了R-积分,但不是R-积分的全部推广,比如广义R-可积不一定是L-可积。从空间完备化观点看,L-积分不过是C[a,b](连续函数类)中函数R-积分的一种完备化扩张[4],可见L-积分具有一定的局限性。因此,人们一直试图寻找一种新的积分。1957~1958年,R.Henstock建立了一种完全Riemann型的积分,称为Henstock积分[5](简称H-积分)。H-积分的本质是“非绝对型”的,因此有时也称之为非绝对型积分。H-积分既推广了L-积分,又包括了Newton积分[6](简称N-积分)和反常R-积分。下面,笔者就非绝对型H-积分理论进行研究:首先给出δ(x)精细分划的定义,然后引进区间[a,b]上的非绝对型H-积分,从而在Henstock引理的基础上给出了H-积分中的Newton-Leibniz公式,并给予了简捷证明。
1 相关定义与引理
定义1[7]设δ(x)为区间[a,b]上的正值函数,所谓[a,b]上的分划D是δ(x)精细的,是指存在有序分点a=x0 ξi-δ(ξi) 即: ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 定义2[5]称实函数f(x)在区间[a,b]上Henstock可积,其积分值为A,如果对∀ε>0,∃实函数δ(x)>0,对区间[a,b]上任作δ(x)精细分划D: a=x0 ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 当ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi))(i=1,2,…,n)时,总有: 或简记为: 其中,[u,v]为分划D中典型区间,满足: ξ-δ(ξ) 若f(x)在[a,b]上Henstock可积(以下简称为H-可积),其积分记为: 定义2与R-积分不同之处在于: 1)R-积分定义中要求δ是正常数,这里的δ(x)为一正值函数而非常数; 2)R-积分定义中先取x1,x2,…,xn-1,再取ξ1,ξ2,…,ξn,此处先取ξ1,ξ2,…,ξn,对每一点ξi,有ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi)),(i=1,2,…,n),假如以上区间组成一[a,b]的覆盖,那么便能取x1,x2,…,xn-1符合以上条件。注意,集合{(ξ-δ(ξ),ξ+δ(ξ));ξ∈[a,b]}形成一开覆盖,根据Heine-Borel有限覆盖定理,肯定能找到一分划D={[u,v];ξ}符合条件ξ-δ(ξ) 例1 令: 则f(x)在[0,1]上是H-可积的。 证明 ∀ε>0,记[0,1]中的有理数为r1,r2,…。令: 取δ(x)精细分划D={[u,v];ξ},有(此处A=0): 式中, ∑1表示各项f(ξ)(v-u)中ξ为有理数时之和。故f(x)为H-可积,且: 注:定义在[0,1]上的Dirichlet函数是R-不可积的[8],但其是H-可积的,可见H-积分也是R-积分的推广。 引理1 (Henstock引理[9]) 若f(x)在[a,b]上H-可积,且有原函数F(x): 则∀ε>0,∃δ(x)>0,使得对[a,b]上的任何δ(x)精细子分划: a≤a1 ξi∈[ai,bi]⊂(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 有: 说明 精细子分划是不要求[a,b]=∪[ai,bi]的精细分划。 证明 由于f(x)在[a,b]上H-可积,故对∀ε>0,在[a,b]上有δ(x)>0,凡δ(x)精细分划所对应的积分和,有: 这样,每个Ji上的δi(x)精细分划与ai,bi,ξi(i=1,2,…,n)构成[a,b]上的δ(x)精细分划,从而: ≤2ε 定理1 若f(x)为[a,b]上N-可积,则f(x)于[a,b]上H-可积。 证明 因f(x)∈N,故∃连续函数F(ξ),有F′(ξ)=f(ξ),其中ξ∈[a,b],从而∀ε>0,∃δ(ξ)>0,当ξ-δ(ξ) |F(v)-F(u)-f(ξ)(v-u)|<ε(v-u) 任作[a,b]的δ(x)精细分划D: a=x0 ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 则有: =ε(b-a) 由ε的任意性得f(x)为H-可积。 定理2 设函数F(x)在[a,b]上连续,且在[a,b]中除去一零测集(测度为0的集)E外,F′(x)=f(x),则f(x)在[a,b]上为H-可积,且: 证明 由假设令E={a1,a2,…}⊂[a,b],∀x∈[a,b]-E,有F′(x)=f(x),故∀ε>0,∃δ(ξ)>0,ξ∈[a,b]-E,∀u,v满足ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))时,恒有: |F(v)-F(u)-f(ξ)(v-u)|<ε(v-u) 又因F(x)在[a,b]上连续,故当ξ=ai时,∃δi>0,使得当u,v满足ai∈[u,v]⊂[ai-δi,ai+δi]时,有: |F(v)-F(u)|<ε·2-i a=x0 ξi∈[xi-1,xi]⊂(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 有: 其中,[u,v]为区间[a,b]上分划D的典型区间;∑分成2项部分和∑1与∑2,∑1取当ξ∈[a,b]-E时的部分和,∑2=∑-∑1。上述不等式的第2项中,当ξ=ai时,因: 故: f(ai)(v-u)<ε·2-i 例2 设: 则: f(x)满足定理2的条件,但f(x)不是L-可积的,而是H-可积的。 非绝对型H-积分推广了L-积分,又包括了N-积分和反常R-积分。Newton-Leibniz公式在非绝对型H-积分理论中占有重要地位,但其证明在相关文献中显得较为复杂,笔者在Henstock引理的基础上给出了该定理的一个简捷证明,改进了相关文献中的证明方法。 [1]李成章.数学分析(上册)[M].第2版.北京:科学出版社,2016:196~201. [2]DonaldLC.MeasureTheory[M].TheWorldBookPublishingCompany,2012:75~78. [3] 王晶昕,王炜,任咏红.实变函数论[M].北京:科学出版社,2016:68~86. [4] 李忠宁.关于R可积函数空间的完备化[J].河西学院学报,2010,26(5):14~18. [5]HenstockR.Lecturesonthetheoryintegration[M].WorldScientific,1988:13~19. [6] 同济大学数学系.高等数学(上册)[M].第7版.北京:高等教育出版社,2014:238~243. [7] 丁传松,李秉彝.广义黎曼积分[M]. 北京:科学出版社,1989:5~8. [8] 何越.狄利克雷函数与黎曼函数的性质[J].河南教育学院学报(自然科学版),2013,22(4):25~27. [9]YeeLP.LanzhouLecturesonHenstockIntegration[M].WorldScientific,1989:15~65. [编辑] 洪云飞 2016-11-15 福建省自然科学基金项目(2015J01585)。 李伟(1962-),男,副教授,现主要从事函数论方面的教学与研究工作。 宋述刚(1961-),男,教授,现主要从事函数论方面的教学与研究工作,2712281782@qq.com。 O171.2 A 1673-1409(2017)01-0040-04 [引著格式]李伟,宋述刚.Henstock积分Newton-Leibniz公式的简捷证明[J].长江大学学报(自科版),2017,14(1):40~43.



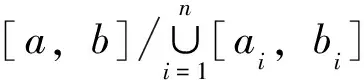
2 主要结论

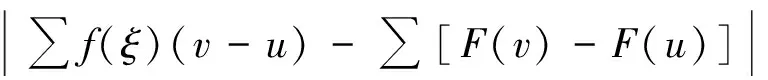
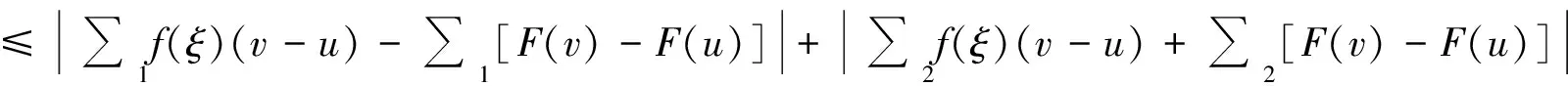
3 结语

