2015年江苏省高考数学卷第19题阅卷感悟

江苏省溧水高级中学(211200) 徐茂炳

2015年江苏省高考数学卷第19题阅卷感悟

江苏省溧水高级中学(211200) 徐茂炳

一、背景分析

笔者参加了2015年江苏高考数学阅卷,试题的解法、评分标准、考生的错误引发了笔者对数学解题教学的一点思考.所阅的是数学卷第19题,阅卷结果如下表：

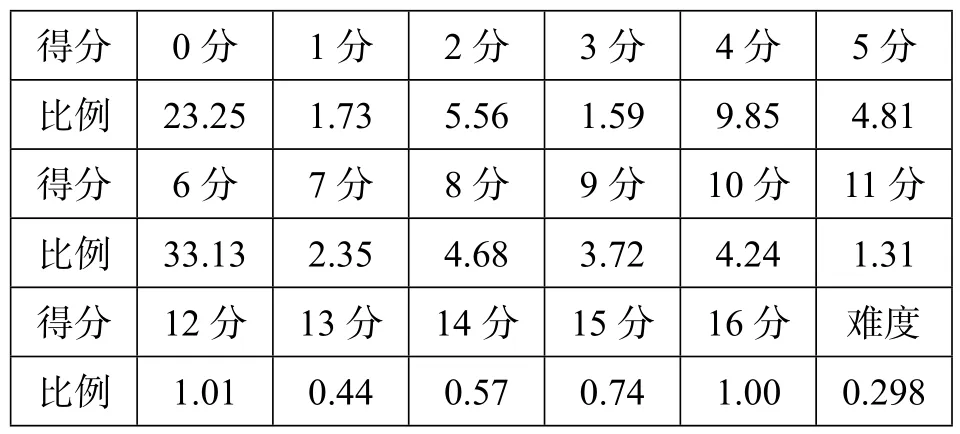
得分_ __0分_ __1分_ __2分_ __3分__ _4分_ __5分比例_ _23.25_ __1.73_ __5.56_ __1.59__ _9.85_ __4.81得分_ __6分_ __7分_ __8分_ __9分__ _10分_ _11分比例_ _33.13_ __2.35_ __4.68_ __3.72__ _4.24_ __1.31得分_ _12分_ _13分_ _14分_ _15分_ _16分_ _难度比例_ __1.01_ __0.44_ __0.57_ __0.74__ _1.00__ _0.298

在阅卷之余,笔者思考面对这样的答题情况,教师该如何教学?由此,我对学生的答题情况进行了分析,对学生所犯的错误进行了归纳,并总结出教学启示“基础牢、审题清、用通法、‘分’点明、计算准、步骤精”,以期为我们的教学提供借鉴和帮助.(本题难度系数0.298)

二、试题回顾

(2015年江苏省高考数学第19题,本小题满分16分)已知函数f(x)=x3+ax2+b(a,b∈R)

(1)试讨论f(x)的单调性;

(2)若b=c-a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是,求c的值.

知识与能力要求 本题主要考查利用导数研究初等函数的单调性、极值及零点问题,第(2)问具有一定的新颖性与挑战性,涉及逆向思维与“恰好成立”问题,考查综合运用数学思想方法分析与解决问题以及代数推理能力.

命题思路及特色 本题以考生熟悉的三次函数为背景,使大多数考生都能入手,考查考生的数学素养和运算求解能力.本题反向提出问题,解决“恰好成立”问题,既要利用“两边夹”思想,先求出c的值,又要代入验证,确保c的值满足“恰好成立”.虽然题面表述简洁,但是思维量较大.

解题思路 (1)利用导数在区间上的正负号,讨论函数在相应区间上的单调性;(2)利用三次函数有三个零点时应具备的特性,结合三次函数有三个零点时a的取值范围,确定c的取值范围;(3)根据所得c的取值范围,讨论三次函数是否确实有三个零点,在保证恰好成立的前提下,最终得到所求c的值.

三、考生出现的错误及其分析

2.第一问考查单调性,单调区间不能用∪连接,f(x)单调递增不交代区间不对(扣2分).但是结论下错了,表格列对了不扣分.所以导数题最好列表;

4.因为评分标准是按步给分,一般一个得分点2分,多一个步骤得2分.因此考试过程中只要时间允许,一定要写到没得写为止,比如一步2分共4分,不少考生认为后面不会做了,所以第二步2分没得到;

5.求导不正确,导数求错或f′(x)=0解出错(常见错误答案) ,平时教学中,一定要重视概念、公式、定理的教学,基本知识是“三基”的根本;

6.审题要认真,准确完整地捕捉题目中的信息是解题的关键,平时教学过程中我们发现很多时候学生会把错误归结到“看错了”.如的解集为当作x的范围,第一问有许多同学将单调性误读为奇偶性(有一人是0分+10分);

7.特殊到一般的思想方法,猜出答案的重要性,只要能得到答案c=1(得4分);

8.有些考生利用变量分离研究交点个数,由x3+ax2+ c -a = 0可知(解不出来).变量分离研究交点个数确实是比较有效的方法,前提是分离后的函数我们一定要能作图,其实就是把一个复杂的图变为两个简单的图研究;

10.函数的零点式可以补充给学生(说清楚即满分) ;

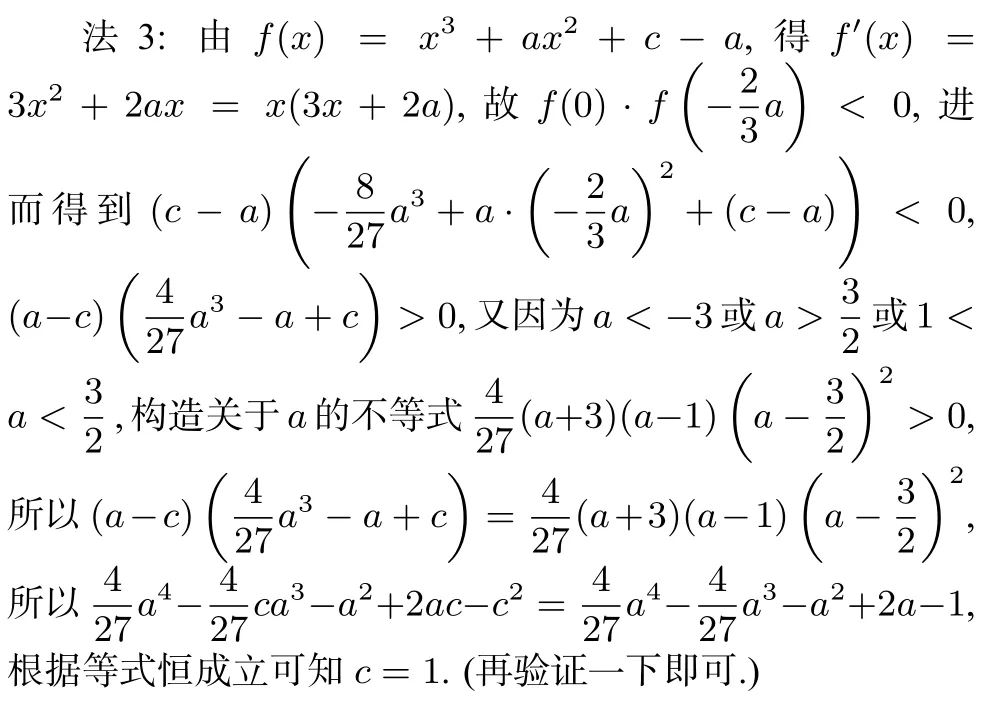
教学过程中有些内容课本进行了淡化或者删除,但是为了知识的完整性和后续学习的需要,我们可以进行适当的补充.如三次函数的零点式、三垂线定理(分析问题)、数量积(投影)、椭圆的第三定义、阿波罗尼斯圆等.

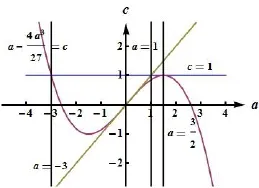
图1

四、复习和教学建议

1.夯实基础是永恒,突出主干知识是根本,理解记忆是保障

在高考卷中基础题和中档题所占比例最重,然而,通过阅卷发现很多学生在基础知识的掌握和基础能力的训练方面非常薄弱,主干知识中的定理条件不清,公式记错等错误比比皆是.所以在教学过程中要夯实基础,突出主干知识落实,狠抓学生的记忆.教师要重视探究概念的形成过程,重视公式定理推导的过程.对重要的概念、公式反复强调,加深学生的记忆和理解.

2.通性通法是主流,淡化技巧是趋势,规范答题是追求

从高考试题中可以明显看出,高考重视对通性通法的考查.现在高考命题的一个原则就是淡化特殊技巧.因此指导学生复习中,不要刻意追求特殊解法,要更多地注重思考题目的“核心”是什么,属于哪类题.阅卷过程中发现很多学生会做不会写,在平时的教学中要帮助学生规范答题,明确题目的通性通法的得分点和解题步骤,要求学生按得分点、步骤书写,严格训练.

3.扎实提升“运算”和“推理”能力

就高考而言,可以说运算准确、合理、迅速是取得好成绩的关键.面对数、代数式的基本运算,能敏锐察觉算式的结构特点,做到心算、估算、假算相结合;至于复杂的运算,则重在“算法”的设计,实际上“运算错误”不仅是技能不过关,更主要的是算法不好.教师要有意识地进行强化训练的同时做到以下几点：一是教师要充分发挥示范、引领、指导的作用,能详细、规范书写解题的推算过程,并对运算细节做必要的解释与说明;二是对让学生上台板演,相互比较“算法”的优劣;三是杜绝计算器的使用;四是对于认为会做的题目而做错了,要求学生通过自己独立、耐心演算得到正确答案.

4.养成良好的解题教学习惯

认真审题是重要的好习惯,有的学生对审题重视不够,匆匆一看急着下笔,无法吃透题目的条件和要求,无法从题目中挖掘隐含条件、启发解题思路.学生的解题习惯很大程度上与教师的解题教学有关.有些教师在例题教学中,学生还没有读完题目就问“你有什么想法?”学生一时答不上来,老师就急着开始讲,久而久之就影响了学生的解题习惯.教师要学会“等待”、“倾诉”,指导学生先写出已知条件,用不同“语言”(文字语言、符号语言、图形语言)表达条件,写出需要求解的具体命题,理清解题思路并标注需要的条件等.