从判断二面角的钝锐说开去
福建省龙海第一中学新校区(363100) 苏艺伟
从判断二面角的钝锐说开去
福建省龙海第一中学新校区(363100) 苏艺伟
在湘教版选修2-1的学习中,学生接触到了利用坐标法求解二面角的余弦值.教材介绍的方法是分别求出两个半平面的法向量,再利用向量夹角公式算出这两个法向量夹角的余弦值,最后结合图形得到所求二面角的余弦值.在最后一步往往需要结合图形对该二面角是钝角还是锐角作出判断.对于较为简单直观的图形还容易判断,如果是较为复杂不明显的图形,学生很难区分出来.那么该如何用数学符号语言给出严谨的判断?除此之外是否可以避开这个难点而直接计算出二面角的余弦值?笔者在长期的教学实践中总结了如下规律.
一、如何判断钝角还是锐角?

图1

图2

图3

图4
如图(1)所示,观察图形可知二面角A-BC-D为钝角;如图(2)所示,观察图形可知二面角A-BC-D为锐角.那么如何用数学符号语言来进行严谨的判断?
作出经过公共棱BC的平面β,使得β⊥面ABC.可以发现图(1)中A和D在β的异侧,图(2)中A和D在β的同侧.也就是说二面角A-BC-D为钝角⇔A和D在β的异侧,二面角A-BC-D为锐角⇔A和D在β的同侧.因此可以借助β来进行判断.
在实际解题中,题目不可能出现β这样的垂面,但是可以自行构造出来,如图(3)所示.步骤如下:
1.建立空间直角坐标系,求出A,B,C的坐标.
2.求出面ABC的法向量
3.以公共棱BC的一个端点如B为起点,构造向量使得求出T点的坐标.此时垂直于面ABC.
4.以直线BT,BC为邻边作出一个平行四边形,该平面必定与面ABC垂直,即为β.
当构造出了垂面β之后,如何借助β来进行判断?

综合上述分析,可以采用如下方法来判断二面角A-BC-D是钝角还是锐角:

例1.2015年安徽高考第19题如图(5)所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(1)略.(2)求二面角E-A1D-B1余弦值.

图5
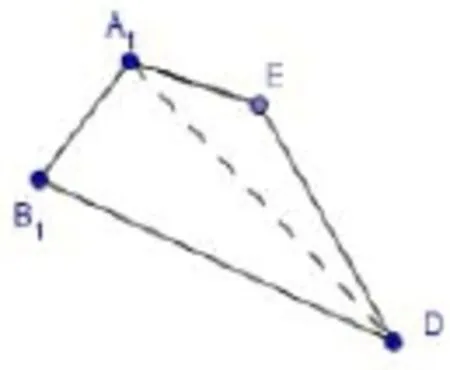
图6


图7
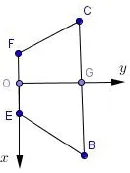
图8
例2.2015年北京高考第17题如图(7)所示,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF//BC,BC=4,EF=2a,∠EBC=∠FCB= 60°,O为EF的中点.(1)略(2)求二面角F-AE-B的余弦值.(3)略.

图9

图10

上述方法是从数学严谨的角度来判断二面角是钝角还是锐角.实际上对于利用坐标法求解二面角的题目,可以绕开这个难点直接求解.
二、利用直线的单向法向量

图11

图12
1.直线关于线外一点的单向法向量.
如图(11)所示,在直线l上取两点A,B,点P为直线外一点.作PC⊥l,垂足为C.则称为直线AB关于点P的单向法向量.

2.如何利用单向法向量求二面角?

上述方法的优点在于避免了根据图形判断二面角是钝角还是锐角.
例3.同例1


例4.同例2

结束语
本文所介绍方法的优点在于能够用严格的数学符号语言代替直观的图形判断,进一步可以避免这个判断上的难点,也就是直接求出二面角的余弦值.本文方法来源于教材又高于教材,能够较好地培养学生的分析能力,运算求解能力,拓展思维.虽然在计算上稍显复杂,但是作为一种课后补充还是可取的.

