略谈不等式成立问题中的函数建构

福建省惠安第三中学(362100) 江志杰

略谈不等式成立问题中的函数建构

福建省惠安第三中学(362100) 江志杰

众所周知,在全国高考或各地高三质检的压轴题中,有关不等式成立问题占据了半壁江山,这类题型最能有效地考查学生的数学思想方法、综合应用能力和学科核心素养,也是一份试卷精华创新之所在.然而在实际问题解决过程中,由于我们缺乏对经典题型进行解法探究与系统归类,导致在该类热点问题上往往出现思维受阻、解答困难的局面,究其原因大都在构造函数方面上出现问题.如何恰当地构造优化的目标函数?如何利用导数工具分析目标函数的性态?探究目标函数的单调性、零点等问题受阻时如何化解?…….为此,笔者就不等式成立问题中函数模型的建构过程略谈一番体会：

一、参变分离原则

不等式中含参数的部分容易“分离”,并且另一端的“无参”函数可求最值时,我们通常采用参变分离法来解决问题.

例1对一切x∈R+,不等式2xlnx≥-x2+ax-3恒成立,求实数a的取值范围.

解析上述不等式中含参数的部分“单一”,参数分离非常容易：a≤x++ 2 l n x ,而对另一端的无参函数g(x)=x++2lnx(x＞0),利用导数知识求其最小值也很常规.一般而言,运用分离参数法必须具备两个基本条件：一是不等式中含参数的部分容易“分离”,二是分离后的无参函数可求最值.

二、通性通法原则

对于研究形如“f(x)＞g(x)”的不等式时,我们通常就是构造左右两端的“差函数”F(x)=f(x)-g(x),分析该目标函数的单调性研究其极值、最值情况.然而在实际的函数导数压轴题中,所构造的“差函数”往往蕴含着参数,这就给目标函数的单调性、极点、零点、最值等性质的研究带来不确定性,需要我们把握分类讨论的依据,罗列所有可能情形逐一分析,方能将目标函数的各种性态研究透彻,进而实现问题的化解!

例2(2015年山东高考理科21)设函数f(x)=ln(x+ 1)+a(x2-x),其中a∈R.

(Ⅰ)讨论函数f(x)极值点的个数,并说明理由;

(ⅠⅠ)若∀x＞0,f(x)≥0成立,求a的取值范围.

例3(2012年全国高考理科21)已知函数f(x)满足

(Ⅰ)求f(x)的解析式及单调区间;

点评由此说明对含参目标函数的单调性进行分析讨论是研究其最值、零点等情况的基础程序,也是解决相应不等式问题的必由之路.因此,我们要充分利用导数工具将各式各样的函数模型淋漓尽致、形象自然地刻画出来!为化解抽象不等式提供具体生动的研究载体!

三、简约可行原则

笔者认为：在建构目标函数模型时,还应注意所构造的函数要进行提炼、简化或变形,否则若因函数结构过于复杂,必然造成求导运算繁琐,难以确定其函数单调性,导致函数性态研究受阻、无法持续.这就需要我们先对所构造的目标函数进行充分“预估、调试、简化”,才能使所构造的目标函数模型优化有效,从而让问题的解决路径得以通畅顺达!

例4(2011年全国高考理科21)已知函数f(x)=曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.

例6(2015年四川高考)已知函数f(x)=-2(x+ a)lnx+x2-2ax-2a2+a,其中a＞0.

(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;

(2)证明：存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在(1,+∞)内有唯一解.

解析(1)略;(2)本题关键证明：存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内的最小值为0(且最小值点唯一).为此需要先确定f(x)的单调性：

点评基于原函数直接求导判断单调性较为困难,我们从原函数结构中分离提炼目标函数,使得利用导数探究函数性态的常规做法持续可行,将不等式问题自然转嫁于研究该目标函数,凸显了化繁为简、化难为易的解题原则.这说明研究函数一定要抓住其“关键所在”,构建函数一定要把握问题的“核心部位”,平常对该类问题的解法要加强反思、不断揣摩、追求优化,才能使目标函数的建构精准到位!

四、搭桥过渡原则

对于某些证明形如“f(x)＞g(x)”的不等式成立时,常规构造“差函数”的做法有时未必奏效,甚至困在“死胡同”.此时我们可以考虑引入中间媒介“h(x)”作过渡,先证明f(x)＞h(x)成立,再证明h(x)＞g(x)成立.“h(x)”可根据f(x),g(x)的图像特征或函数性态来确定,h(x)有时可能是一条“隔离直线”,也可能是个数值,关键视实际问题不断尝试、调整.比如证明不等式ex-lnx＞2成立,我们可以根据函数y=ex和y=lnx的图像走势,以及它们与其相应切线的位置关系,先证明ex＞x+1(x＞0)成立,再证明x+1≥2+lnx即x-1≥lnx成立,便可实现证明.又如：

例7(2014年全国高考理科 21)设函数 f(x)=,曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.

(Ⅰ)求a,b;

(ⅠⅠ)证明f(x)＞1.

例8(2015年北京高考理科18)已知函数f(x)=

点评本题第(ⅠⅠ)小题的设置是个很好的搭桥过渡,无疑为第(ⅠⅠⅠ)小题的分类讨论埋下了伏笔、减轻了分类讨论的力度.倘若没有第(ⅠⅠ)小题作阶梯,直接求第(ⅠⅠⅠ)小题必然显得很棘手!这说明k=2是函数f(x)大于右侧函数的“临界状态”,而我们所要寻找的中间过渡或枢纽往往就在于发现这样的临界状态!

五、设而不求原则

解决不等式成立问题时,经常让我们受困的是所建构的目标函数求导后仍是繁杂的超越函数,无法确定其零点,从而造成目标函数的单调性、极点、极值等也相应无法确定.为此,笔者提出构设导函数的辅助零点,突破导函数“无法求解”这一瓶颈,打通原函数研究的常规思路,巧妙利用导函数零点存在的等量关系进行代换,从而实现导函数零点的“设而不求”.比如前面证明不等式ex-lnx＞2成立,也可从常规通法入手,解析思路如下：

点评本题最值一提的是求出fmin(x)=f(x0)= ex0-lnx0之后,其范围依然未知,但通过导函数f′(x)的对应方程隐藏的等量关系进行替换,将“超越式”转化为“整式”,再利用均值不等式巧妙地使x0的构设达到“设而不求”的效果!

例9若不等式x(1-k)+k+xlnx＞0对任意x＞1均成立,求整数k的最大值.

点评该例充分说明构设导函数零点处理超越函数的综合问题有着广阔的应用空间,其做法极具实效性、典范性!

六、一元归化原则

遇到求解有关二元不等式成立的综合问题时,需要认真分析不等式结构,从中提炼二元函数模型：y=(x1,x2),但如何研究二元函数又是一个挑战,唯有转换为一元函数去解决.事实上,很多二元函数y=(x1,x2)可围绕或x1x2等进行适当的配凑变形,再令其中或t=x1x2等,即可转换成关于t的一元函数y=φ(t)来解决,这是一种常见的化归策略.

例10(2011年辽宁高考理21改编)已知函数f(x)= lnx-ax2+(2-a)x.

(Ⅰ)讨论f(x)的单调性;

(ⅠⅠ)若函数y=f(x)的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明：f′(x0)＜0.

七、执果索因原则

某些不等式(如二元不等式)的证明,并不能象上述直接轻易地构建出目标函数,而是从所要证明的目标开始分析,逐步探求使结论成立的充分条件,在追溯解决问题线索中自然产生构造函数、研究函数的需要,这种函数建构针对性强、目标清晰、规避模式,有利于提升分析问题和解决问题的综合能力.

例11(2016年全国新课标Ⅰ理21改编)已知函数f(x)=(x-2)ex+a(x-1)2(a＞0).

(Ⅰ)求函数f(x)的单调区间和极值;

(ⅠⅠ)设x1,x2是f(x)的两个零点,证明：x1+x2＜2.

解析由f′(x)=(x-1)(ex+2a)可得：f(x)的递增区间为(1,+∞),递减区间为(-∞,1),故其在x=1处取得极小值f(1)=-e.第(Ⅰ)小题的设置让我们获得了函数f(x)的大致轮廓;

第(ⅠⅠ)小题可由第(Ⅰ)小题结果以及函数值的符号、趋势,勾勒出函数f(x)=xe-x的示意图,图中直线x=1是函数f(x)的“类对称轴”,由于“类对称轴”两边增减幅度不同,当f(x1)=f(x2)时,可直观发现：x1+x2＜2,这就是第(ⅠⅠ)小题的问题产生的原始背景.

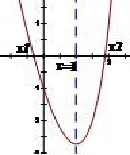
图1

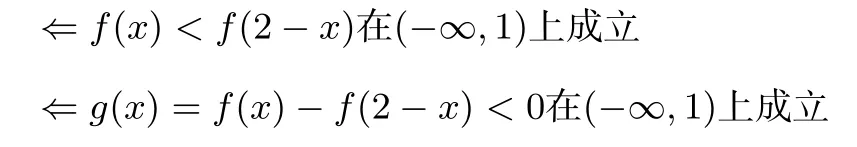
于是解决问题的切入点转为常规的构造函数运用导数知识证明不等式恒成立问题.

例12 若函数f(x)=ex-a(x-1)存在两个零点x1,x2(x1＜x2),求证：x1x2＜x1+x2.

结束语上述典例充分说明：求解有关不等式成立问题终究还是化归为函数问题的探究,目标函数的建构是整个解决问题过程中的关键和主线,合理恰当的函数模型是持续发挥导数功能的基础载体,是有效化解不等式问题的重要依托,也是渗透常见数学思想的上佳素材.函数建模受挫并不可怕,关键在于灵活运用已有的知识储备,寻求问题的变通、解法的突破和思维的创新.