上有思想的复习课

郝雪松

我曾经听了几节数学复习课，课堂上，老师带着学生把这一阶段的知识点一一回顾，然后设计一些相关练习来巩固知识点。表面上看，这些复习课上得面面俱到，四平八稳，但我认为作为复习课应该具有一定的思想和深度。

其实，学生经过一段时间学习的积累，特别是期末复习甚至是毕业前的总复习，对于知识的重新认识就会高于新授课时或单元复习时。因此，教师在复习时，不但要帮助学生梳理知识，使知识系统化，更要帮助学生掌握知识背后的思想，让那些具有生长性的数学思想成为学生后续学习的动力源。

本着这种认识，我精心组织了一节数学复习课《面积与转化》。

课堂片段：

师：小学阶段，我们学习了哪些平面图形？

生回答。

师：关于它们的面积，课前让同学们自己做了整理。谁愿意把整理好的成果跟大家分享呢？

生回答长方形、正方形、平行四边形、三角形、梯形和圆形的面积公式。

师：其他同学有什么补充吗？

生：平行四邊形的面积，是通过转化推导出来的。

师：你能具体说说吗？

生：沿着平行四边形的一条高剪开，把它平移到平行四边形的另一侧，这样就转化成了长方形，长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，因为长方形的面积等于长乘宽，所以得到平行四边形的面积等于底乘高。

师：转化的过程，你记得真清楚。

生：三角形和梯形，它们的面积也是运用转化的思想推导出来的。

生：三角形和梯形的面积，因为是两个完全一样的图形拼成的平行四边形，所以要除以2。

生：圆的面积在推导过程中，是把圆化曲为直，转化成长方形，转化后面积不变，周长变了。

生：平行四边形和圆的面积是通过转化成长方形来研究的，而三角形和梯形的面积是通过转化成平行四边形来研究的。

师：说得真好！看来同学们课前做了认真而充分的准备。现在老师把这些知识点用一幅图呈现给大家。（课件出示）

师：从下往上看，是知识的生长过程，从上往下看，是学习知识的思想——转化。

当研究新图形遇到困难时，往往通过转化成学过的图形来解决，转化这种思想不仅应用于平面图形的研究，数学的很多地方都会需要它，如立体图形（圆柱的体积），计算题、应用题等等，它是数学上一种很重要的学习思想。

对于复习题的选择和使用，应该本着“题尽其用”的原则，做到一题多用，一题多变。因为尽管题目的内容和类型多种多样，但它们都具有思想的一致性和思维的相似性，这样让学生学会举一反三、融会贯通地解决问题，从而达到通过一题解决多题的效果。我为本节复习课设计了以下练习。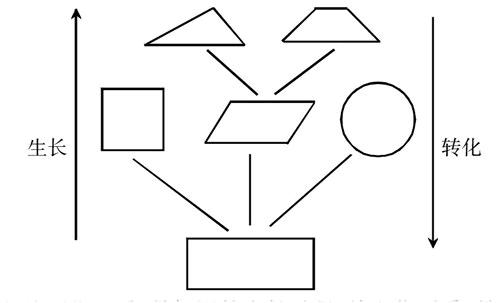

一、填空题

1.一个平行四边形的面积是280平方厘米，与它等底等高的三角形的面积是（ ）平方厘米。

2.一个三角形的高是7分米，底是8分米，和它等底等高的平行四边形的面积是（ ）平方分米。

3.一个三角形和一个平行四边形的面积相等，底也相等，如果三角形的高是10米，那么平行四边形的高是（ ）米；如果平行四边形的高是10米，那么三角形的高是（ ）米。

二、判断题

（1）两个面积相等的三角形可以拼成一个平行四边形。

（ ）

（2）等底等高的两个三角形，面积一定相等。（ ）

（3）梯形的面积等于平行四边形面积的一半。 （ ）

（4）平行四边形的面积等于长方形面积。（ ）

（5）把用木条钉成的长方形拉成一个平行四边形，它的高和面积都与原来相等。（ ）

三、应用题

1.一个梯形上底长6米，下底长9米，高是5米，在这个梯形中画一个最大的长方形，那么这个长方形的面积是多少平方米？

2.将一个圆沿半径剪开，再拼成一个近似的长方形。已知这个长方形的周长是41.4厘米，那么，这个圆的周长和面积各是多少？

3.在一个长5厘米，宽4厘米的长方形内画一个最大的圆。这个圆的周长和面积分别是多少？

四、开放题

在方格纸上画出面积相等的三角形和梯形。

在学生练习之后，我和学生对本节复习课进行了总结。

师：今天的复习课，你有什么新的收获？

生：我们复习了六种平面图形面积公式的推导过程。

生：通过一幅图我知道了这六种图形之间有着密切的联系。

生：我知道在这些图形面积的推导过程中，运用了转化这种数学思想。

生：转化的思想不仅应用于平面图形面积的学习，在其他数学学习中也经常用到。

数学思想是对数学知识和方法的本质认识，是对数学规律的理性把握，学生数学思想的形成要经历从感性认识到感悟理解的过程，复习课应该成为这一过程的桥梁。

参考文献：

[1]陈晓梅.如何上好整理复习课[J].小学青年教师，2005（5）.

[2]过峰艳.小学数学复习课新模式初探[J].现代中小学教育，2003（4）.