基于多个低秩纹理提取的图像校正方法

马金辰，谢世朋，李海波

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于多个低秩纹理提取的图像校正方法

马金辰，谢世朋，李海波

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

低秩纹理是图像处理领域中具有重要几何意义的结构，通过提取低秩纹理可以对畸变或受损图像进行有效校正；但现有的基于低秩纹理提取的图像校正方法只能把感兴趣区域看作一个整体，从而导致许多复杂情况下的校正无法获得理想结果。针对上述问题，对现有算法进行改进，实现感兴趣区域的多个低秩纹理分别提取，用以解决实际应用中的多种畸变和受损图像的恢复问题。对选定区域进行分割，对每个子区域分别进行低秩校正，加强初始化窗口对纹理的适应性，从而优化校正效果。大量实验结果表明，该方法可以有效处理同一感兴趣区域中的多个低秩纹理，在凸平面、多个不兼容区域和复杂纹理等多种情况下仍然可以获得正确的处理结果,且校正效果与原算法相比更加符合人眼视觉特性。

低秩纹理；增广拉格朗日乘数法；图像分割；多分辨率；分支定界

0 引 言

图像校正技术的研究在图像处理领域具有十分重要的应用，如智能交通管理系统中的车牌识别、超市条形码录入等。近年来，基于图像特征点和显著区域提取的图像校正方法受到学者的广泛关注，然而现有的检测对称区域和模型的校正方法，几乎都是通过提取和重组如边缘、角点[1-2]等局部特征实现的。由于特征检测和边缘提取本身就对噪声、遮挡和光照改变等区域图像变化比较敏感，故这种对称性检测方法缺乏鲁棒性和稳定性。另外，由于拍摄角度、噪声等因素对获取图像造成的畸变和干扰会严重影响图像的识别、分析及判断，且人的视觉感知系统具有不变性[3]，所以基于视觉不变性的纹理分析及图像校正方法十分必要。众所周知，现有的广泛使用的不变特征描述(Scale Invariant Feature Transform，SIFT)[4]虽然在很大程度上关于旋转和缩放具有不变性，但是当多幅图像由不同视角获取时，SIFT则无法建立可靠的对应。

现有研究表明，通过消除空间变换(如仿射和投影)，可以从2D图像中提取不变性信息，这些信息对应于3D图像表面的大量规则模式，且可以被近似模型化为“低秩”矩阵。一个具有这种低秩纹理的图像受到特定的空间变换后的纹理矩阵，通常不再具有低秩性。文献[5]中Candes等基于稀疏理论，提出可通过运用先进的凸优化算法来实现矩阵秩的最小化，因此可以从一幅畸变图像中同时恢复低秩纹理及其畸变量。文献[6]中提出一种名为RASL的图像对齐算法，该算法同样应用稀疏低秩恢复模型实现图像的可靠对准，但该算法无法利用图像的空间结构，且需处理多幅图像中的多个空间变换，从而导致算法的复杂度过高，能够解决的问题有限。文献[7]中提出的变换主成分分析方法，结合离散的隐变量，使用期望最大化算法提取主成分和空间变换。但是使用该方法进行图像校正时需要提前预知矩阵的秩，并且只能处理小范围的高斯噪声，这大大限制了其在实际中的应用范围。

Yi Ma等提出名为TILT(Transform Invariant Low-rank Textures)的图像校正方法[8]，该方法直接使用图像(窗口)的原始像素值，而不需要对图像进行任何局部特征的预提取；且对于由干扰、遮挡或杂乱背景所造成的少量误差，具有较强的鲁棒性。文献[9]对该算法进行优化，解决了算法的收敛性问题，并提高了算法处理速度。虽然上述TILT算法可以校正大量近似低秩的纹理(如人脸和印刷文本)，且校正结果较好，但是该算法具有一定的局限性：当选中窗口内包含多个不兼容区域，或各子区域受到的畸变不同时，该算法就无法实现图像的正确校正。

针对上述问题，对TILT算法进行改进，将感兴趣区域分割为多个子区域，从而优化算法的初始化窗口，达到在复杂情况下校正图像的目的。通过实验对比文中算法与原算法的处理效果，结果表明优化后的算法可以成功处理原算法无法解决的部分复杂问题。

1 基于低秩纹理提取的图像校正原理

假设存在一个低秩纹理A(x,y)，从特定角度所观察到的图像D(x,y)是原始低秩纹理函数A(x,y)经过变换后的形式：D(x,y)=A∘τ-1(x,y)=A(τ-1(x,y))。其中，τ为一个R2→R2的旋转变换函数，为方便计算，假设τ既包含旋转变换又包含2D仿射或投影变换。除了空间变换，现实观察到的纹理图像还可能受到噪声或遮挡的影响，或者包含一些背景像素。将这些干扰量模型化：D=A+E。其中，E为误差矩阵。文中仅考虑低秩纹理图像受损部分远小于纹理本身的情况，即E为稀疏矩阵。则从畸变或受损图像中恢复低秩纹理A即解决以下问题：

已知一个畸变和受损的低秩纹理图像：D=(A+E)∘τ-1，恢复低秩纹理A和空间变换τ。

上述表达式可导出如下形式的优化问题：

(1)

优化的目的是求得可能的具有最低秩的纹理A，并使噪声矩阵E尽量稀疏，且E符合由空间变换τ所决定的观察矩阵D。此处，γ>0为权衡误差稀疏度和纹理的秩的加权参数。

事实上，初始问题(1)中秩函数和E的零范数都很难进行优化解决，但最近在稀疏表示和低秩矩阵恢复方面的研究突破已经表明[10-11]，这两个问题都可以用其凸优化方法解决：分别用矩阵A的核范数(Nuclearnorm)‖A‖*来代替rank(A)，用矩阵E的1范数‖E‖1来代替‖E‖0。因此，式(1)可以转化为：

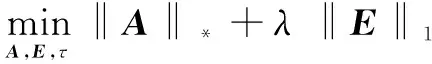
(2)

将约束条件线性化[12]为如下形式：

D∘τ+JΔτ=A+E

(3)

其中，J是雅可比行列式。

则式(1)中的优化问题转化为：

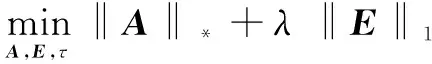
A+E

(4)

上述的线性问题为凸问题，且能够用凸优化的方法高效解决。在解该线性问题时，需要使用迭代的方法在各局部解得最优值(最小值)，并最终求得全局最优值(最小值)。

具体算法总结如下：

算法1：

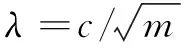
whilenotconvergeddo

步骤(1)：归一化和计算雅阁比矩阵J。

步骤(2)(内循环)：求解线性问题。

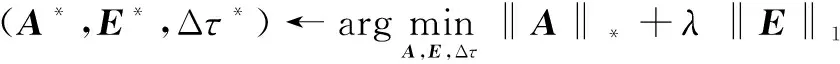
步骤(3)：更新变换：τ←τ+Δτ。

endwhile

输出最优解：A*,E*,Δτ*。

算法1中，计算量最大、最耗时的部分是迭代循环过程的内部循环(步骤(2))，可以使用增广拉格朗日乘子法(ALM)[13]对其进行解决。对于问题(4)，增广拉格朗日方程定义为：

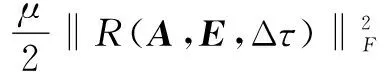
(5)

其中，μ>0,Y为拉格朗日乘数矩阵，且：f(A,E)=‖A‖*+λ‖E‖1,R(A,E,Δτ)=D∘τ+JΔτ-A-E。

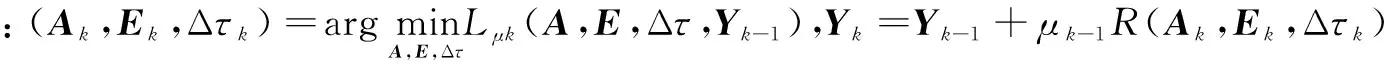
一般情况下，使变量A,E和Δτ同时最小化的计算量十分巨大。因此可采用交替方向法[14]，对A,E和Δτ逐个求最优解：

(6)

式(6)的解可以通过使用收缩算子的方法转化为以下形式：

(7)

2 算法的优化处理

2.1 区域分割

上述TILT算法运用凸优化理论，实现了从畸变和受损图像中快速提取低秩纹理和畸变量。但是，当需要处理的图像区域包含多个不同的低秩纹理时，该方法不再适用。这是由于多个受到不同畸变的低秩纹理组合而得的矩阵，不能再分解为一个低秩矩阵A和稀疏矩阵E的和。当感兴趣区域为多个不兼容区域的组合时，低秩纹理恢复问题转化为：

(8)

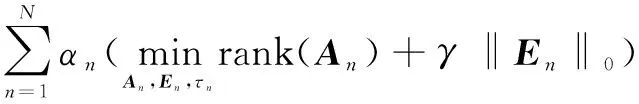
Dn∘τn=An+En

(9)

其中，N为分割后的子区域个数；αn为加权系数，由子区域畸变强度和受损情况决定。

由式(9)可得线性凸问题：

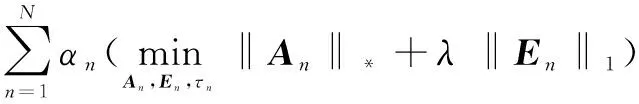
(10)

对于式(10)，直接求解十分困难，可将其转化为：

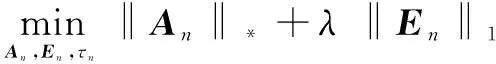
JnΔτn=An+En，n=1,2,…,N

(11)

问题(11)的增广拉格朗日方程为：

Yk=Yk-1+μk-1R(Ak,Ek,Δτk)

(12)

引入交替方向法：

(13)

(14)

为了消除由缩放坐标造成的影响，假设变换前后图像的面积及边长比不变，即：S(τ(Ω))=S(Ω)且L(τ(e1))/L(τ(e2))=L(e1)/L(e2)。该假设对于问题(2)添加了额外的非线性约束条件，与式(3)的方法类似，这些非线性约束条件可转化：

AsΔτn=0

(15)

优化后的算法可总结为算法2的形式。

算法2：

输入:输入图像D∈Rm×n。

(1)whilenotconvergeddo

(2)while1≤n≤Ndo

(4)Jn(Dn∘τn)=max(‖Dn∘τn‖2,‖Dn∘τn‖),E0=0,Δτ0=0,μ0>0,ρ>1,k=0

(5)whilenotconvergeddo

(8)Yk+1=Yk+μk(Dn∘τn+JnΔτk+1-Ak+1-Ek+1)

(9)μk+1=ρμk,k=k+1

(10)endwhile

(11)An=Ak,En=Ek,Δτn=Δτk,τn=τn+Δτn

(12)endwhile

(13)endwhile

(15)输出最优解：

(16)

实验中，令t1=5×10-5,t2=10-7。

算法2通过区域分割，弥补了原算法无法同时处理多个不兼容区域的缺点，可以在更多复杂情况下获得较好的校正结果。

2.2 多分辨率方法

虽然算法2在实际应用中能取得很好的实验效果，但当低秩纹理中存在任意形状的尖锐特征或轮廓时，算法会收敛到一个局部最小点，而无法得到正确解。因此，为了处理大的畸变，可以引入多分辨率方法[15-16]。多分辨率方法是计算机视觉领域一种广泛使用的技术，该方法从输入图像开始，逐渐对图像进行下采样，降低分辨率。可首先通过在最低分辨率的图像上运用算法2进行低秩纹理校正，并用最低分辨率下获得的最优解对高一级分辨率图像进行初始化，以此类推。

事实上，多分辨率方法不仅提高了算法可以处理的变换范围，也极大地优化了算法的运行时间。这是因为，在低分辨率下凸问题能够更快速地求解，并且，由于较高分辨率下的程序得到了更好的初始化，使得迭代至收敛的次数明显减少。

2.3 分支定界方案

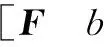
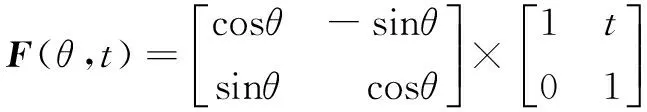
(17)

可将参数空间(旋转和偏斜)分割成多个区域，并对这些区域逐个进行贪婪搜索。首先采用不同的旋转角度初始化并运行算法2，然后选择使价值函数最小的初始值，用这个初始值依次沿着x轴和y轴方向搜寻偏斜参数。使价值函数最小的参数就是分支定界方案的输出值。

对于这样一个分支定界方案，需要考虑其是否具有较高的效率。在多分辨率优化策略中，只需要在最低分辨率水平下使用分支定界，并找到最优解，然后使用这个解来初始化较高分辨率的图像。因为算法2对于较小的矩阵在低分辨率下具有很快的运行速度，所以运行不同初始值的多个过程并不会对整体速度有太大影响。实验结果表明，当采用多分辨率策略时，分支定界方案能使迭代次数进一步减少，虽然每次迭代所需时间略微增加，但总体时间是下降的。

为分析多分辨率方法与分支定界方案对算法的影响，在处理器主频为1.4GHz，软件环境为Windows7的PC机上，对大小为153×68的图像在四种情况下分别处理，实验结果如表1所示。

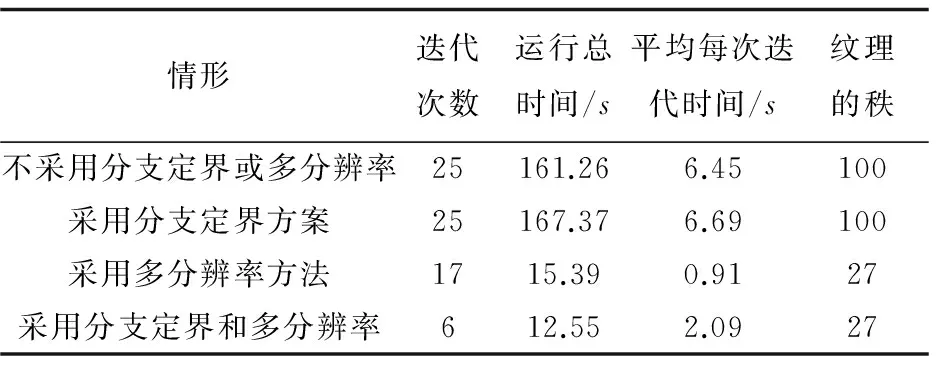
表1 实验结果对比

3 实验结果及分析

本节进行了大量实验，用以验证文中算法的有效性。如图1所示，文中算法可以处理如建筑物表面、标牌、文本和车牌等多种低秩纹理的校正，且校正效果十分理想。

除上述简单情况外，在多种复杂条件下进行实验，并将文中算法与原算法进行对比，实验结果如图2所示。其中第一行为原始图像及输入窗口，中间行为原TILT算法校正结果，最后一行为文中算法校正结果。

图1 算法对多种纹理的处理效果

图2(a)为凸平面的纹理校正，由于试图校正的区域关于图像垂直中轴受到不同程度的投影变换，所以把整个区域看作整体进行低秩校正的方法会导致区域边缘处效果不佳。从图中可以看出，使用区域分割后，校正效果有所改善。

图2(b)、(c)和(d)中，感兴趣区域包含两个相邻的低秩区域，且两区域受到不同程度的畸变。原TILT算法以其部分区域为准对整个窗口进行空间逆变换，这使得另一区域受到了更大程度的畸变。如图所示，文中算法在这种情况下具有非常好的效果。

图2(e)中，输入窗口的图像纹理较复杂(即秩较高)，使用文中算法对窗口进行分割，使初始窗口更加适应纹理方向，可以优化实验结果。

图2(f)中的图像受到的畸变程度过大，原算法只能实现一定程度的校正，效果不理想。如图所示，文中算法的校正效果明显提高。

图2 文中算法与原算法在复杂情况下的对比

4 结束语

针对多低秩纹理图像的校正问题，将图像区域分割与低秩提取算法相结合，提出一种新的更有效的图像校正算法。该算法通过将感兴趣区域分割为多个子区域，优化纹理提取的初始化窗口，并采用多分辨率方法和分支定界方案，提高算法的收敛域和运行速度。实验结果表明，该算法可以解决大量多低秩纹理图像的校正问题，且校正效果更加符合人眼视觉特性。

[1]HeX,LiJ,WeiD,etal.Cannyedgedetectiononavirtualhexagonalimagestructure[C]//Jointconferencesonpervasivecomputing.[s.l.]:IEEE,2009:167-172.

[2]BruceNDB,KornprobstP.Harriscornersintherealworld:aprincipledselectioncriterionforinterestpointsbasedonecologicalstatistics[C]//IEEEconferenceoncomputervision&patternrecognition.[s.l.]:IEEE,2009:2160-2167.

[3] 吴永兴.图像纹理旋转不变性分析[D].天津:天津大学,2007.

[4]LoweDG.Distinctiveimagefeaturesfromscale-invariantkeypoints[J].InternationalJournalofComputerVision,2004,60(2):91-110.

[5]CandesEJ,RechtB.Exactlow-rankmatrixcompletionviaconvexoptimization[C]//46thannualallertonconferenceoncommunication,control,andcomputing.[s.l.]:IEEE,2008:806-812.

[6]PengYigang,GaneshA,WrightJ,etal.RASL:robustalignmentbysparseandlow-rankdecompositionforlinearlycorrelatedimages[J].IEEETransactionsonPatternAnalysis&MachineIntelligence,2011,34(11):2233-2246.

[7]FreyBJ,JojicN.Transformedcomponentanalysis:jointestimationofspatialtransformationsandimagecomponents[C]//ProceedingsoftheseventhIEEEinternationalconferenceoncomputervision.[s.l.]:IEEE,1999:1190-1196.

[8]ZhangZ,GaneshA,LiangX,etal.TILT:transforminvariantlow-ranktextures[J].InternationalJournalofComputerVision,2012,99(1):1-24.

[9] 马 杰,张小美,苑焕朝.基于并行分离增广拉格朗日乘子法的字符矫正[J].光电子·激光,2015,26(6):1170-1178.

[10]ZhaoYQ,YangJ.Hyperspectralimagedenoisingviasparserepresentationandlowrankconstraint[J].IEEETransactionsonGeoscience&RemoteSensing,2014,53(1):296-308.

[11]CandesEJ,TaoT.Thepowerofconvexrelaxation:near-optimalmatrixcompletion[J].IEEETransactionsonInformationTheory,2009,56(5):2053-2080.

[12]BakerS,MatthewsI.Lucas-Kanade20yearson:aunifyingframework:part4[J].InternationalJournalofComputerVision,2004,56(3):221-255.

[13]MaF,NiM,TongW,etal.MatrixcompletionviaextendedlinearizedaugmentedLagrangianmethodofmultipliers[C]//Internationalconferenceoninformativeandcyberneticsforcomputationalsocialsystems.[s.l.]:IEEE,2015:45-49.

[14]LiW,ZhaoL,XuD,etal.Efficientimagecompletionmethodbasedonalternatingdirectiontheory[C]//2013IEEEinternationalconferenceonimageprocessing.[s.l.]:IEEE,2013:700-703.

[15]JoshiA,BhaskarV.Multi-resolutionapproachformedicalimageregistrationusinggeneticalgorithm[C]//Internationalconferenceoncommunicationsandsignalprocessing.[s.l.]:IEEE,2013:612-616.

[16] 李万朋.基于低秩纹理的旋转不变特征提取算法研究[D].秦皇岛:燕山大学,2013.

[17]XieShipeng,LiChunming,LiHaibo,etal.Alevelsetmethodforcuppingartifactcorrectionincone-beamCT[J].MedicalPhysics,2015,42(8):4888-4895.

[18]TanH,ChengB,FengJ,etal.Tensorrecoveryviamulti-linearaugmentedlagrangemultipliermethod[C]//2011sixthinternationalconferenceonimageandgraphics.[s.l.]:IEEE,2011:141-146.

Image Rectification Method Based on Multiple Low-rank Textures Extraction

MA Jin-chen,XIE Shi-peng,LI Hai-bo

(School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Low-rank textures play an important role in image processing fields.By extracting the low-rank textures accurately,the distorted or damaged image can be rectified effectively.However,the existing methods based on texture extraction always rectify the region of interest as a whole,which makes it comes to nothing in many complex cases.Aiming at the above-mentioned problems,an improved rectification algorithm is proposed based on multiple low-rank textures extraction.The new rectification algorithm is able to extract multiple low-rank textures respectively and solve a large number of problems of image renewing for distorted or damaged images in practical application.In order to optimize the experimental results,the selected regions are segmented and each sub-region is rectified respectively which can enhance the adaptability of the initialization window to the texture.Experimental results demonstrate that the proposed method is able to rectify multiple low-rank textures in the same region of interest.In complex circumstances such as convex plane,multiple incompatible regions,complex textures and so on,the ideal processing results can be obtained with it.Further more,the results are more in accord with human vision characteristics,which is a critical evaluation criteria.

low-rank textures;augmented Lagrangian multiplier method;image segmentation;multi-resolution approach;branch-and-bound scheme

2016-04-21

2016-08-11

时间：2017-02-17

国家自然科学基金资助项目(11547155)；江苏省自然科学基金(BK20130883)；南京邮电大学引进人才基金(NY213011，NY214026)

马金辰(1993-)，女，硕士，研究方向为图像处理；谢世朋，副教授，研究方向为图像处理。

http://www.cnki.net/kcms/detail/61.1450.TP.20170217.1628.030.html

TP391.41

A

1673-629X(2017)03-0097-06

10.3969/j.issn.1673-629X.2017.03.020