例谈图形的全等分割

王翠玲

[摘 要] 背景图形不同，分割要求不同，对应的分割方案也不同. 如以正方形为背景，把确定分割线的问题转化为以正方形的中心为中心找成中心对称的点；如在“非对称图形的全等分割”中，把“非对称图形”转化为学生熟知的“对称图形”——矩形，以降低探究难度，破解分割障碍.

[关键词] 全等分割；折线型；曲线型；旋转

全等图形是初中几何的重要内容之一，是学生从单一图形过渡到复杂图形的认知基础，其中全等图形的分割设计是一项有意义、富有挑战的教学活动. 在活动中，教师应首先引导学生分析已知图形——“父图”的特征，抓住“全等图形指的是两个图形能够完全重合”的内涵，根据要求进行全等分割，获得“子图”. 下面结合一些图例，与大家一起分享.

图例赏析

（一）以对称图形为背景

1. 以圆为背景

例1 要在圆形的空地上种植4种不同颜色的花，每种颜色的花集中种植，且所占地面的形状、大小都相同，请画出设计方案（分割线用实线表示）.

“种植4种不同颜色的花，每种颜色的花集中种植，且所占地面的形状、大小都相同”，也就是把圆分割成4个全等的图案. 如图2，根据圆的轴对称性可知互相垂直的两条直径便把圆分割成4个全等的扇形，这是绝大部分学生都可以想到的最基本的设计方法.

这种方法所呈现的分割线是直线，我们称之为“直线型”，该方法很容易被学生理解和接受，但此时学生的思维处于浅层次运作状态.

教师可以再设置以下问题，引导学生探索不同的分割方法：

（1）分割后，每一部分的面积与原来图形面积有何数量关系？

（2）“直線型”中的每一个扇形的圆心角是多少度？你能利用旋转验证“直线型”的合理性吗？

（3）分割线一定是直线吗？折线、曲线行吗？

学生借助问题导航，根据分割要求（把圆分割成4个全等的图案），通过独立分析、尝试画分割线、小组合作交流等方式可以获得不同的分割方法，笔者将其分割方法分为两大类——“折线型”和“曲线型”.

折线型 如图3、图4，巧用旋转画折线.

如图3，以折线0AB为基础分割线，以点O为旋转中心依次旋转90°，每经过一次旋转得到一处分割线（如折线ODC，OFE，OHG）. 从图形直观感知，我们可以看出此时分割的目的已经达成.

对于几何图形问题，我们重视几何直观的同时，也要重视合情说理. 如根据要求“把圆分割成4个全等的图案”，教师可以引导学生从图形构成着手，认识到每一个图形的面积等于圆的面积的1/4，理解“折线型”实质上是在“直线型”的基础上进行割补而已：如将原有（图3）的扇形OCB中“割”去△AOB，又“补”了与之全等的△COD，利用等式性质——以算代证，可知SBAODC=S扇OCB，且整个圆可以看作是由4个具有旋转关系的全等“子图”构成的. （类似的，我们还可以设计图4“法西斯”式的折线图）

曲线型 如图5、图6、图7，巧用旋转画曲线.

“折线型”和“曲线型”是在“直线型”基础上的再创造，是“直线型”的一种“转型”，每一种分割方法都渗透着转化、全等变换等思想. 如以4个全等扇形为基础，以等式的性质为算理，在每一个对应区域顺次剪裁一个全等的图形，使相邻扇形的不同部分组合成新的图形，从而获得四等分全等分割. 殊途同归，学生也可以以基本图形为原型（如图5中的基本图形是），从图形旋转的角度（依次旋转90°）进一步理解分割方案，这对于深化学生对全等图形的认知、拓宽学生的思维，大有裨益.

2. 以正方形为背景

例2 已知正方形ABCD，要求将其分割成两个全等图形.

教师可以设置以下问题串，引导学生思考、探索不同的分割方法：

（1）分割后，每一部分的面积与原来图形的面积有何数量关系？

（2）正方形是轴对称图形吗？是中心对称图形吗？对称中心是什么？

（3）在例1中“把圆分割成4个全等图形”，我们运用了90°的旋转角，而例2要求把正方形分割成两个全等图形，我们能否也从旋转的角度进行思考？旋转角应该是多少度？你有什么分割猜想？

（4）分割线可以是直线吗？折线、曲线行吗？

“如果我们成功地回想一个以前求解过的与我们当前的题目有某些相关的题目，我们就很幸运. 我们应该努力争取并获得这样的幸运. ”教师要善于启发学生迁移、类比相关知识，引导学生积极捕捉“幸运”知识链条. 显然，类比例1的背景图形——圆，例2中的正方形既是轴对称图形也是中心对称图形，其分割方法有可借鉴之处. 幸运的是，通过学生的积极思考、尝试分割，也获得了“直线型”“折线型”和“曲线型”等分割方案.

方法1 “直线型”，这是一种简单易懂的分割方法，如图8、图9、图10，过对称中心的任意一条直线均是符合要求的分割线.

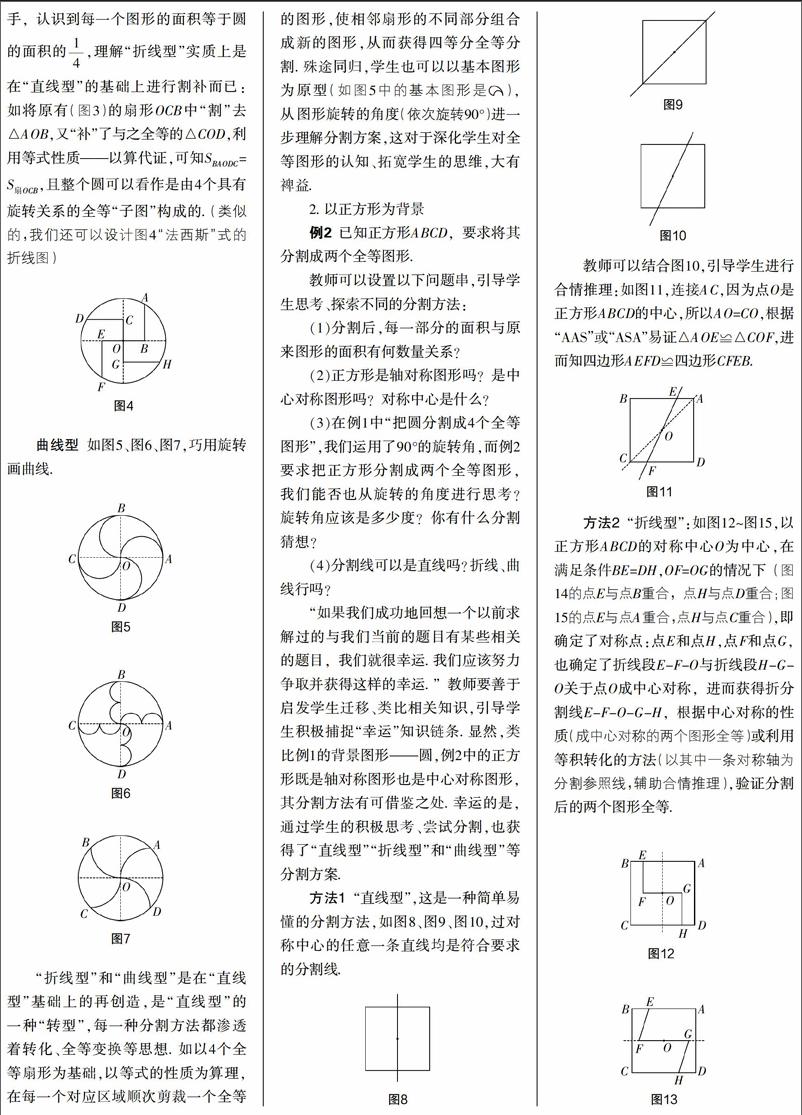
教师可以结合图10，引导学生进行合情推理：如图11，连接AC，因为点O是正方形ABCD的中心，所以AO=CO，根据“AAS”或“ASA”易证△AOE≌△COF，进而知四边形AEFD≌四边形CFEB.

方法2 “折线型”：如图12～图15，以正方形ABCD的对称中心O为中心，在满足条件BE=DH，OF=OG的情况下（图14的点E与点B重合，点H与点D重合；图15的点E与点A重合，点H与点C重合），即确定了对称点：点E和点H，点F和点G，也确定了折线段E-F-O与折线段H-G-O关于点O成中心对称，进而获得折分割线E-F-O-G-H，根据中心对称的性质（成中心对称的两个图形全等）或利用等积转化的方法（以其中一条对称轴为分割参照线，辅助合情推理），验证分割后的两个图形全等.

方法3 “曲线型”，如图16和图17，与“折线型”相似，以中心对称为理论依据（旋转角为180°），在满足相同条件下有规则地画关于中心O对称的弧线. 如图16，直线EF是正方形的对称轴，分别以OE，OF为直径在正方形的对称轴两侧画半圆，这两个半圆关于中心O成中心对称，所获得的两部分为全等图形， 则为分割线. 学生根据已有的推理经验，以正方形的对称轴为辅助线，运用“割补”转化的方法，易证分割后的“子图形”对应全等.？摇

3. 变式：以网格线的对称图形为背景

例3 用不同方法沿网格线把正方形分成两个全等的图形.

其实，分割方法仍然类似，关键是确定对称点、确定对称线段，即抓住对称中心发散线路（如图18，点A，B关于中心O的对称点分别是点D，C，则分割线为A-B-O-C-D）. 与前例不同的是，此题中的关键词是“沿网格线”，则对分割方法加以限制：分割线只能是水平的或竖直的，不能是斜线或曲线（如图18、图19）.

例4 把图20中的网格图形用一条折线沿网格线分割成两个全等图形. 请画出两种不同的分割方案，然后与同伴交流你的发现.

菱形既是轴对称图形，也是中心对称图形. 根据轴对称性，学生容易获得“直线型”分割方案（如圖21，AB是分割线）；根据中心对称性，学生借助已有的活动经验（以菱形的中心O为中心，确定对称点线段，即抓住对称中心发散线路）可以获得不同的分割方法，如图21、图22、图23和图24.

对称图形是初中几何学习的“重头戏”，所以以对称图形为背景研究全等图形应作为全等分割教学的重点，而在非对称图形中探究全等分割，可以培养学生的创新思维.

（二）以非对称图形为背景

例5 在图25中沿网格线把图形分割成两个全等形.

设小正方形的边长为1，与“4×4型（边长为4）”正方形相比，相当于上面的“1×4型（宽为1，长为4）”矩形向右平移了1个单位长度. 根据正方形的轴对称性，教师引导学生猜想：原对称轴经过“1×4型”矩形的部分是不是也应向右平移一个单位长度？

学生通过动手画图，获得图26所示的分割线，并进行操作验证（平移），感受这种通过对比、关联图形而联想到的方法. 对于这种分割方法，教师引导学生换一个角度分析，数学体验也有所不同.

从整体上看，背景图形不具有对称性，而从图形组合的视角进行剖析，它可以看成是由几个矩形组合而成的，而每一个矩形是对称图形！此时便将复杂的非对称图形转化为简单的对称图形，搭建起顺利进行全等分割的“脚手架”.

思路1 背景图形可以看成是由两个矩形构成的：“1×4型”“3×4型”（图27）. 根据两个矩形的对称性，我们分别获得分割线AB，CD，再连接BC，即运用A-B-C-D将该图进行了全等分割，获得与图26一样的分割线. 显然，同一种分割方法，思考角度不同，数学理解不同，学生会滋生不同的知识生长点.

从不同视角分析图形，我们会获得不同的结论，也可以获得不同的方法. 对于该背景图形，我们还可以进行如下分析与分割.

思路2 背景图形可以看成是由3个矩形构成的：“1×4型”“2×4型”“1×4型”.

首先突破分割难点：把两个“1×4型”矩形看作对应部分，沿网格线进行合理分割，再把“2×4型”矩形进行合理等分，并使得分割线完美对接，即把这个图形分割成两个全等图形. 如图28，其中的两个“1×4型”矩形分别被AB，CD分割成1个正方形和3个正方形，“2×4型”被全等分割，则折线A-B-E-C-D即为分割线.

图29中的两个“1×4型”矩形不分割，而是利用折线A-B-C-D-E-F-G将“2×4型”进行分割，并与“1×4型”矩形对应组合，构成倒“F”型的全等图形.

对于以上图形的分割方案的合理性，学生可以运用翻折、平移等方法进行验证和感悟.

教学思考

1. 充分理解图形

美国著名数学家G·波利亚指出“理解题目”的重要性：“如果学生还没有理解题目，就着手计算和画图，那就可能发生最糟的事了. ”所以，拟定全等分割方案的前提是充分理解图形.

（1）立足图形本身性质

全方位的观察已知图形，充分了解图形本身的性质，这是正确设计全等分割的首要条件. 教师应引导学生从图形蕴含的性质出发，根据分割要求不断调整分割线、修正分割线，以获得创意纷呈的分割线和全等图形. 因此，在教学中，教师应重视对几何图形基本条件和性质的教学，为学生搭建好深入探究问题的脚手架.

（2）多角度的辩证分析图形

以前文的“非对称性图形背景”为例，其组成方式不唯一，站在“由两个矩形构成”的视角我们得到图27的方案，站在“由3个矩形构成”的视角我们得到图28、图29的方案. 从不同角度审视图形能获得不同的灵感，绽放不同的思维火花，收获不同的分割方案，这种“多角度分析图形”是形成多元化策略的基础.

背景图形是一个整体，亦是分成的几个全等图形的合体：沿分割线“分”“合”交替，整体可以分为若干全等的个体，个体亦可以合成完整的整体——“多图合一”，即恢复成原来的背景图形. 教师可以利用几何画板操作、演示等手段，引导学生辩证地分析图形，让学生体会图形的“分”与“合”的多种策略，感受图形之间蕴含的辩证思想，理解整体与个体的关系，增强对各种设计方案的感性认识，充分感受几何图形设计之妙.

2. 挖掘关联性知识点

有的学生图感很好，能较快地获得分割线，但对于为什么这样分割，这样分割有什么理论依据，如何验证，由此带来的数学知识还有哪些，却不清楚，此时教师应正确引导和点拨，让学生“知其然，亦知其所以然”，以培养学生严谨的数学品质，并获得丰富的数学体验.

如以上图例中，教师引导学生借助轴对称、中心对称分析图形，链接平移、旋转、翻折等进行操作验证，进一步感受常见的全等变换的应用. 在教学中，教师应“小题大做”，高角度审视原命题，理解题目蕴含的更深层次的知识点，契机设疑、追问，巧妙联系、过渡，融入相关联的知识点或对原命题进行拓展变式.

3. 关注数学思维

（1）多种策略，延展思维的宽度

优秀的教师总是“勤”字当先，从不拘泥于一个视角或一种解法，不以获取答案作为解题终结目标，而是善于引领学生多角度分析问题，努力培养学生勤思考、勤探究的良好学习品质，并不断提高学生的数学素养和解题能力.

在本文图例中，学生在掌握背景图形性质的前提下，从不同角度动手尝试画图，形成不同全等分割方案；学生在探究多种解题策略的同时，积累了分析图形的经验，拓宽了数学思维，有效提高了解题能力和思维水平.

（2）推理验证，培养思维的严谨性

每一种全等分割策略形成之后，教师都应引导学生合情推理，验证方案的正确性和可行性，这有利于培养学生思维的严谨性，并使学生逐步形成理性的、缜密的思维习惯.

4. 渗透数学思想

数学思想是数学的精髓和灵魂. 前文图形的全等分割策略中应渗透转化的思想方法，如例2，我们把确定分割线的问题转化为以正方形的中心为中心找成中心对称的线段，进而转化为找成中心对称的点；如例5，我们引导学生把“非对称图形”转化为学生熟知的“对称图形”——矩形，降低了探究难度，破解了分割障碍. 把复杂的问题转化为简单的问题，把未知问题转化为已知问题，这种转化的思想方法是探究学习的基本策略.

背景图形不同，条件不同，分割要求不同，对应的分割方案不同，教师要引导学生寻求有用的思路：“从不同的方面来考虑问题，强调不同的部分，考察不同的细节，从不同的途径反复考察同一细节，以不同的方式组合这些细节，从不同角度来处理它们”，并由此使学生生成不同的数学思考，积累丰富的活动经验，不断提高解题能力和思维水平.