外形促建构 意义促提升

杨凯明

在乘法的运算律中，乘法分配律是一个重点。学生在学习乘法分配律时，难在对其意义的理解及灵活运用。尽管教学时提供了大量素材和实例作表象支撑，但学生在概括乘法分配律的定义时，总不如概括交换律和结合律那么顺畅和准确。学生对于乘法分配律的认识要达到抽象化和精致化，就需要在学习中有一个不断积蓄的过程，要让乘法分配律不再成为难点，就需要幫助学生建立乘法分配律的不同结构，逐渐建立起意义层面上的理解。教师不能只把目光聚焦在知识的获得上，更重要的是学生学习方法的获得。课堂中要让学生经历“建构等式——猜想规律——验证规律——得出结论——再次猜想”的过程，以直观、具体的形式呈现学习素材，便于学生理解、建模。

一、在感知中形成表象

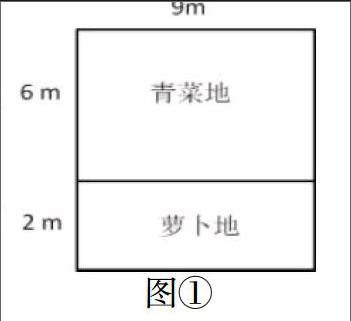
1.课件出示图①菜地。

青菜地长9米，宽6米；萝卜地长9米，宽2米。

（1）你能算出两块菜地的总面积吗？

（2）交流算法，板书两种不同的计算方法。

（6+2）×9=72（平方米） 9×6+9×2=72（平方米）

比较：这两位同学算两块菜地的总面积有什么不同吗？

生：一个是把这两块地拼成一个新的长方形再算它的面积一个是把两块地的面积分别算出后再相加。

师：那有没有相同的地方？

生：得数相同，都表示两块菜地的总面积。

师：说明左边这个算式等于右边这个算式。

板书得到等式：（6+2）×9=6×9+2×9

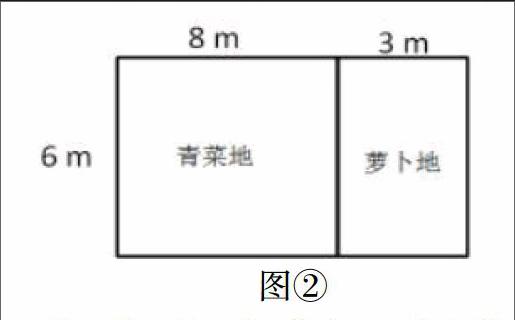
2.课件出示图②和图③两块菜地。

青菜地，长8米，宽6米；萝卜地，长6米，宽3米。

图②

青菜地，长8米，宽5米；萝卜地，长7米，宽6米。

（下转第18页）

（上接第17页）

图③

（1）求出他们各自菜地的总面积。

图②的面积：（8+3）×6=66（平方米） 8×6+6×3=66（平方米）

师：都等于66，看来我们也可以用“=”连接。

板书得到等式：（8+3）×6=8×6+3×6。

（2）思考：为什么图③的两块菜地不能合起来算呢？8×5+7×6

（因为拼不成一个长方形，没有一条共同的边）

（3）提问：图①和图②的菜地总面积可以合起来算的原因是什么？（有一条边相等）

小结：有一条边是共同的，就可以把两块地的面积合着算。

【评析】运算定律的学习对于学生来说是相对抽象的，将长方形的面积计算与乘法分配律的知识融合在一起，从图形出发，数形结合，以计算长方形面积为载体，建构等式，使学生在探究的过程中进一步对这样的等式有深入的了解，明确探究的方向。在学生交流讨论图③不能列出等式原因的过程中，让学生体会乘法分配律中必须有相同因数这一重要的数学本质。

二、在理解中掌握内涵

1.刚才我们写出了几组相等的算式，他们有什么共同的特点？

（6+2）×9=6×9+2×9

（8+3）×6=8×6+3×6

提问：这两种算式相等你认为是偶然的还是必然的？你还能举出这样的例子吗？写一写，并验证一下左右两边是否相等。

2.这样的例子举得完吗？有没有符合这样规律的算式但左右两边不相等？你有其他方法来说明这两种算式必然相等吗？

3.看来这样的例子是写不完的，那谁能写出一个能包含所有这些例子的等式？

4.抽象规律：两个数的和与一个数相乘，可以先把他们与这个数分别相乘，再相加，这就是乘法分配律。

5.（板书：4×7+6×7）谁来结合这个算式说明下我们发现的这个乘法分配律是成立的。（课件出示下图的3个素材）

4个7加上6个7合起来就是10个7，也就是（4+6）×7。

小结：看来，乘法分配律也可以用乘法的意义几个几来解释，而且从右边到左边也是成立的，也就是a×c+b×c=（a+b）×c。

6.回顾旧知，深化学生对乘法分配律的认识。

（1）回顾两位数乘一位数的口算（课件出示）。

（2）回顾长方形周长的计算（课件出示）。

【评析】在学生举出大量等式的基础上引导孩子进行观察猜想，并且从正反两个方面对得出的猜想进行验证，再从乘法的意义解释乘法分配律，掌握其内涵。抽象出结论后，让学生用数学语言表述其规律。在整个教学过程中，学生自主地经历了乘法分配律的探究过程，抽象、概括的能力得到了发展。引导学生回顾乘法和长方形周长的计算，经历演绎推理的思维过程，沟通了新旧知识之间的联系，又使数学思维得到进一步的提升。

三、在练习中发展能力

1.运用规律填空。

（42+35）×2=42×□+35×□

27×12+43×12=（27+□）×□

15×26+15×14=□○（□○□）

2.初步拓展到两个数的差与一个数相乘。

出示：（6-2）×9=□○□○□○□

师：这道算式，刚学的乘法分配律适用吗？你有什么办法来验证？

得出：乘法对加法的分配律可以推广到乘法对减法的分配律。

3.再次拓展到三个数或更多的数的和与一个数相乘。

猜想、验证：如果把乘法分配律中“两个数的和”换成“三个数的和”、“四个数的和”或更多个数的和，结果还会不会不变？

【评析】通过题组的比较和练习，让学生学会根据数据特点，灵活运用乘法分配律，避免生搬硬套，培养思维灵活性。将乘法分配律由“两个数的和”拓展到了“两个数的差”，再提出“多个数的和与一个数相乘”是否适用于乘法分配律的猜想，这是一种很有价值的思考。从已有的结论中通过适当的变换、联想，同样可以形成新的想法，进而形成新的结论，在类比推理中形成新的结论。