声速剖面插值方法在多波束测深中的应用

闫循鹏，卜宪海，刘洪霞，辛明真，阳凡林，2

(1. 山东科技大学 测绘科学与工程学院，山东 青岛266590；2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室，山东 青岛266590)

声速剖面插值方法在多波束测深中的应用

闫循鹏1，卜宪海1，刘洪霞1，辛明真1，阳凡林1，2

(1. 山东科技大学 测绘科学与工程学院，山东 青岛266590；2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室，山东 青岛266590)

声速剖面通常采用站位式测量得到，分布较为稀疏，即使是走航式测量也难以得到足够密集的声速剖面。为此应在现有的声速剖面基础上进行插值以满足各方面的需要。反距离加权插值法、线性插值三角网法和基于经验正交函数的声速剖面反演法是声速剖面插值常用的三种方法，文章讨论了其在多波束测深声速剖面加密中的适用性和插值精度。结果表明，三种声速剖面插值方法均可提高声速改正精度，其中基于经验正交函数的声速剖面反演法插值精度高，适用性好；线性插值三角网法内插精度较高，但外推能力较差；反距离加权插值法算法简单，便于实现。

声速剖面插值；反距离加权插值法；线性插值三角网法；经验正交函数

声速改正是多波束测深数据后处理的关键步骤之一，其所采用的声速剖面的准确性直接影响着波束点归位计算的精度[1-3]。目前国内有关多波束测量的规范对于声速剖面的测量、区域分布和站位密度没有特殊要求[4-5]，通常情况下进行声速改正时采用“最近原则”法，即采用距离测深位置最近的声速剖面。若声速剖面采集站位布设不合理，或在声速变化复杂地区，如大陆架浅水区、河口冲淡区，声速剖面采集具有滞后性，将会引入较大的声速剖面代表性误差，从而影响多波束测深最终成果质量，造成假地形[6]。为此，Cartwright[7]在声速结构变化较快地区采用走航式声速剖面仪来获取较为密集的声速剖面，但此方法通常无法采集到表层和底层声速值。关永贤[8]提出了在多波束数据后处理中利用现有声速剖面采用反距离加权插值法(inverse distance weighting，IDW)进行插值，得到了更为密集的声速剖面。LeBlanc[9]等的研究表明，经验正交函数(empirical orthogonal function，EOF)是描述声速剖面有效的基函数，并利用此函数构建了深海声速场模型。我国学者[10-13]在基于EOF的声速剖面反演法上也取得了一些研究成果，其中部分研究成果已应用于多波束测深声速改正中。声速剖面插值虽在多波束测深数据处理中得到一定的应用，但目前对各种方法的插值精度和适用性分析较少。本文以实测和模拟的声速剖面数据为例，比较分析了反距离加权插值法、线性插值三角网法(triangulation with linear interpolation，TLI)和基于EOF的声速剖面反演法在多波束测深声速剖面加密中的插值精度和适用性，对多波束测深中声速站的布设和声速改正有一定的参考价值。

1 声速误差对多波束测深精度的影响

1.1 表层声速误差对多波束测深的影响

海水表层温度和盐度易受日、风、海流等因素影响，表层声速变化大，若未利用表层声速仪实时采集表层声速，会带来表层声速误差，其对多波束测深的影响主要体现在波束指向角的准确性上，从而影响多波束测深精度。

多波束平面阵换能器预形成波束时需要预知表层声速，例如，当预形成第k个波束时，波束指向角θk与表层声速c0的关系为[14]：

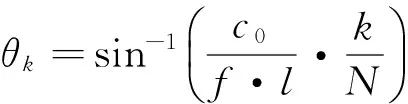
(1)

式中，N为水听器基元个数，k∈(-N/2，N/2)；f为水听器频率；l为基元间隔，通常取l=λ/2；λ为声波波长，且c0=λf。从上式可以看出，当换能器发射频率一定时，预形成的波束指向角只与表层声速c0相关。现取实际表层声速c0=1 500m/s，f=100 kHz，N=57，水深d=100 m的条件下预生成波束指向角，在对表层声速c0分别添加±1、±2、±3m/s的误差后，对实际波束指向角的影响如图1(a)所示，其对多波束测深的影响如图1(b)所示。

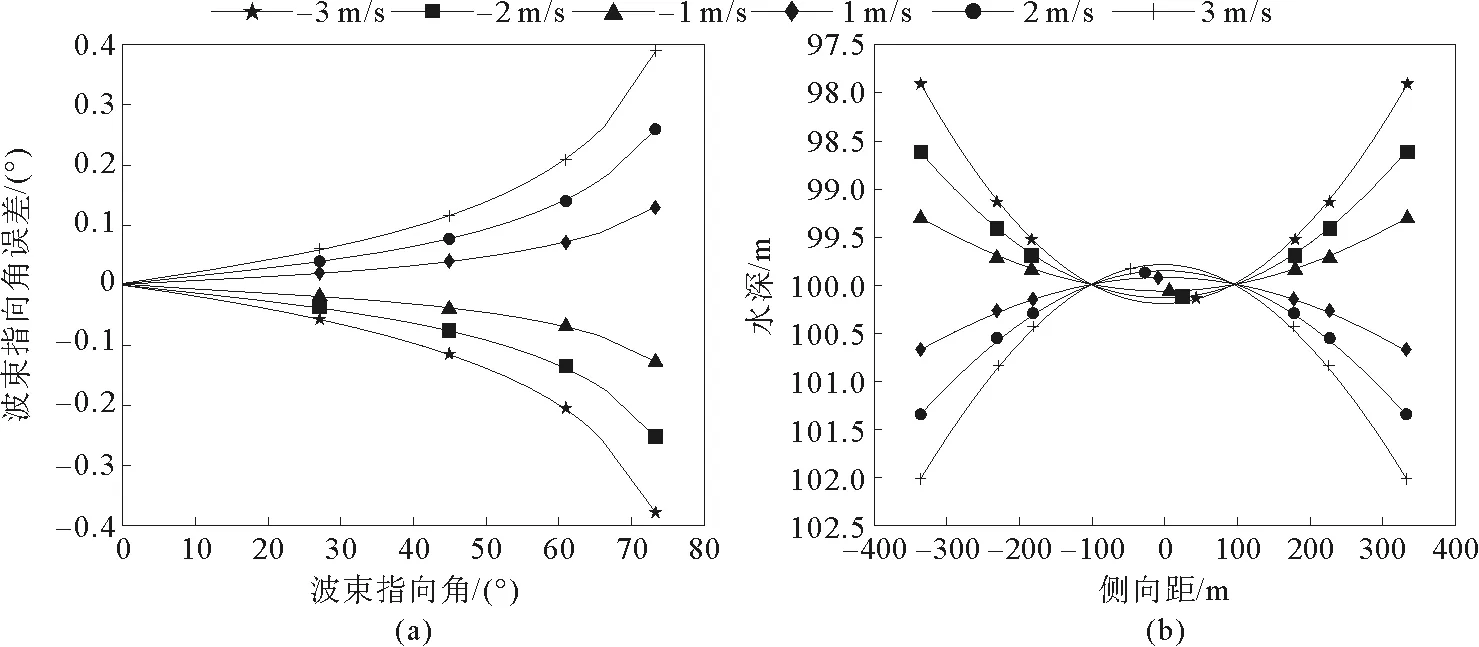
图1 表层声速误差对多波束测深的影响

从图1中可以看出，入射角为0°的中央波束指向角不受表层声速误差的影响，随着波束入射角和表层声速误差的增大，波束指向角误差也逐渐增大，在波束入射角大于60°时，波束指向角误差增大速度加快。当设定的表层声速大于实际表层声速时，波束指向角较原来增大，多波束条带覆盖宽度增加，测得的海底地形整体呈现出“哭脸”状失真，即中央波束附近水深小于实际水深，边缘波束水深大于实际水深；当表层声速小于实际表层声速时，结果相反。此外，在表层声速误差为2m/s、指向角为75°时，波束指向角误差达0.26°，水深误差达1.39m，超过了1%水深的限差，故表层声速误差应限定在1m/s内。

1.2 声速剖面代表性误差对多波束测深的影响

相邻的声速剖面结构具有相似性，但又无明显的规律性，为了研究声速剖面代表性误差对多波束测深的影响，假设相邻声速剖面存在整体偏差，即声速剖面各声速节点加减同样的值，声速梯度保持不变，且不考虑表层声速变化对波束指向角的影响。取一实测的声速剖面，并对声速剖面的各声速节点分别添加±2、±4、±6m/s的误差形成6个新的声速剖面，预设水深d=54 m，结合常梯度声线跟踪算法，对比各声速剖面对同一海底的声速改正结果，如图2所示。

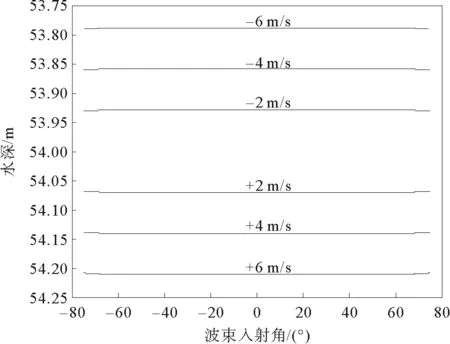
图2 声速剖面代表性误差对多波束测深的影响

由图2可知，当声速剖面整体偏小时，声速改正后的水深减小，边缘波束略向下弯曲；当声速剖面整体偏大时，声速改正后的水深增大，边缘波束略向上弯曲。声速剖面整体偏差越大，水深误差越大，整体偏差6 m/s，水深误差达0.24 m，已接近1%水深限差的一半。

可见，表层声速误差和声速剖面代表性误差均会影响多波束测深精度，且对边缘波束影响更大，故声速剖面个数采集不足或测区海洋环境复杂时应采用合理的插值方法加密声速剖面。

2 声速剖面插值方法

2.1 反距离加权插值法

反距离加权插值法又称为距离反比法，认为被估未知点属性与其周围一定距离内离散的已知点的属性有关，利用这些已知点的数值进行加权运算即可以求取未知点数值，各已知点所给予的权重依据已知点与未知点的距离远近来确定，距离未知点越近的权重越大，即

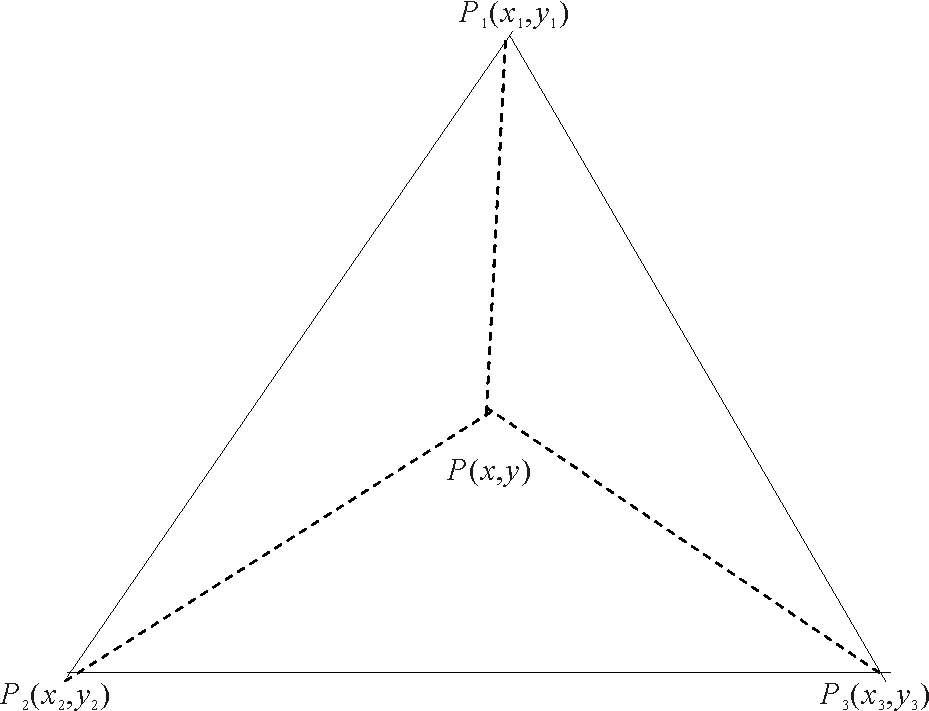
图3 线性插值三角网法示意图

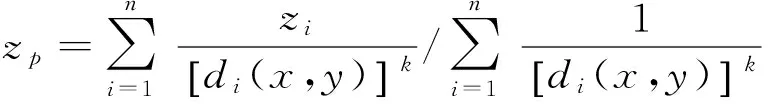
(2)

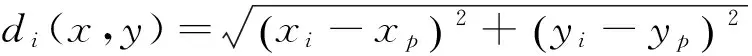
2.2 线性插值三角网法

线性插值三角网法需要将所有站位中相邻的三个点连接成三角形，并且所有三角形的边都不能与其余任意一个三角形相交叉，从而构成一个覆盖整个测区的三网形平面网。三角网中每个三角形内的任意一点P(x,y)均位于该三角形三个顶点确定的平面上，其数值由三个顶点加权运算求取，权系数由点P与三个顶点之间的线性关系确定。如图3所示：

插值函数为：

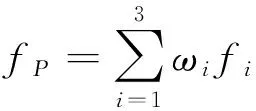
(3)

式中，fi为顶点P(xi,yi)(i= 1,2,3)的已知数值，ωi为相应的权系数：

(4)

由于确定权系数ωi的前提是待估点P位于三角形内部，因此对于三角网外部的点线性插值三角网法不再适用。

2.3 基于EOF的声速剖面反演法

基于EOF的声速剖面反演法是一种对同一测区内具有空间相关性的声速剖面进行特征向量分解，并结合采样数据重构该测区任意一点声速剖面的反演方法。

原始的m个声速剖面数据节点通常是非等深采样，需对每一条声速剖面进行样条插值得到n个垂直分布的等深节点，则内插后的声速剖面矩阵为：

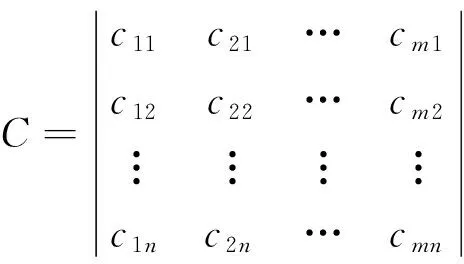
(5)

C的协方差矩阵R：

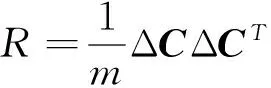
(6)

对协方差矩阵R进行特征分解得到：

RF=DF，

(7)

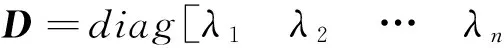
测区内任意一点的声速剖面c(z)可用前k阶EOF表示为：

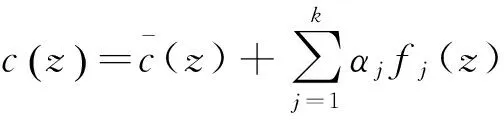
(8)

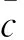
3 实例计算与分析

3.1 三种插值方法插值精度评定

2015年9月在黄海某区域共采集了14个站位的声速剖面，站位分布及三角网法构建的三角网如图4所示，声速剖面结构如图5所示。现选取其中12条声速剖面作为已知数据，2条声速剖面a和b(站位如图4所示)分别用于检核插值算法的内插与外推能力。

从图4和图5中可以看出，此次野外采集的声速剖面站位分布得不是很均匀，声速剖面结构总体相似，但在水深约5 m处存在着声速跃层，呈表层声速变化较大、底层声速稳定变化、个别声速剖面结构与其他声速剖面结构差异略大的态势，有明显的时空分布差异。首先，对原始声速剖面进行等深节点插值处理，再分别利用上述三种方法对检核剖面a和b所在位置进行插值，并将插值结果与实测和最邻近声速剖面对比，如图6所示。

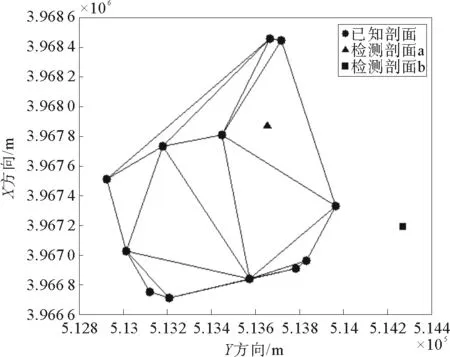
图4 声速剖面站位分布

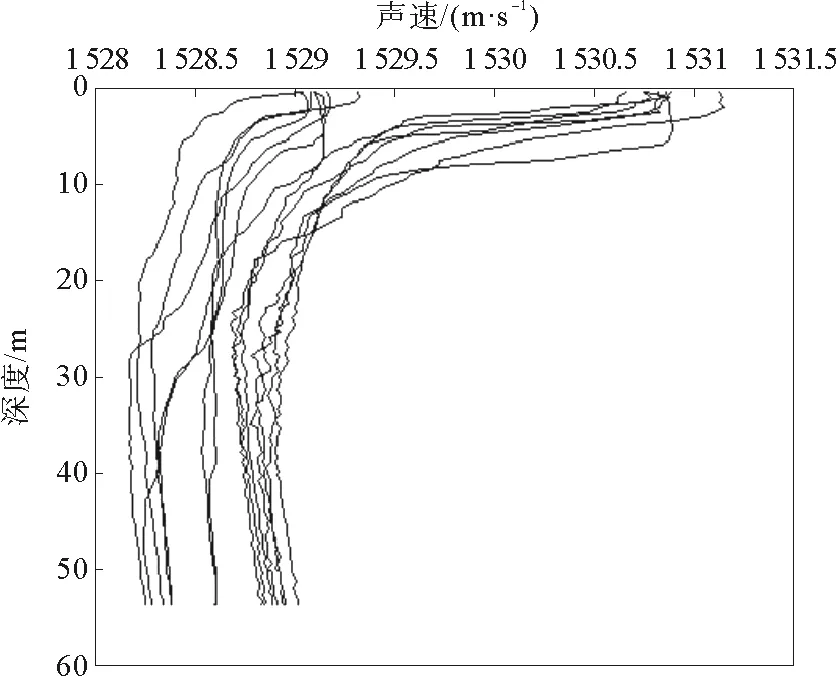
图5 声速剖面样本结构图

图6 实测声速剖面与内插声速剖面对比

数值插值方法的好坏通常通过交叉验证进行评价[15]。交叉验证的主要评定指标有平均误差、均方根误差和标准残差等，其中均方根误差越小，待插点的预测值就越接近于其真实值，即插值方法越好。a和b两站声速剖面插值结果残差统计如表1所示。

表1 残差统计结果

通过上述图6和表1可以发现：

1) 在内插时,即a站位处，三种插值方法的内插精度较采用“最近原则”均有所提高，其中基于EOF的声速剖面反演法各指标数值较小，即插值精度最高，反距离加权插值法和线性插值三角网法次之，插值精度大致相似。

2) 检测剖面b位于构建的三角网外，线性插值三角网法不再适用，退化为“最近原则”法，外推精度大为降低；反距离加权插值法均方根误差最小，精度最高；基于EOF的声速剖面反演法精度虽有所下降，但适用性仍然较好。

3) 将检测剖面a、b插值结果对比可知，若插值处站位距离已知声速站位较远，各插值方法的插值精度均会下降，采用“最近原则”法选取声速剖面进行声速改正时，误差会迅速增大，最大达2.05 m/s。因此，在多波束外业测量中，应根据已有资料尽量满足声速站采样的密度要求。

3.2 三种插值方法对多波束声速改正的影响

为了分析三种插值方法对多波束声速改正的影响，利用同一组多波束回波时间观测序列，分别采用实测和插值得到的声速剖面进行声线跟踪，并以实测声速剖面的声线跟踪结果为基准，计算a、b两站位内插的声速剖面引起的水平位移误差和深度误差，如图7和图8所示。

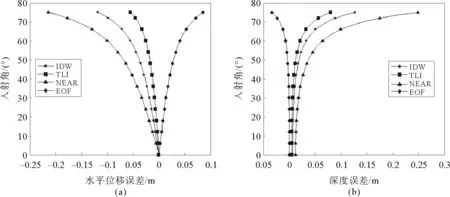
图7 a站位三种声速剖面插值方法对多波束声速改正的影响

图8 b站位三种声速剖面插值方法对多波束声速改正的影响

从图7和图8中可以看出，若采用传统的“最近原则”法选取声速剖面进行声速改正时，随着波束入射角的增大，引起的多波束测深误差也逐渐增加，造成条带边缘处地形上翘或下弯。在波束入射角大于65°时，a、b两站最大测深误差分别达到0.25和0.45 m，后者已接近《海道测量规范》限定的1%水深误差。但在采用声速剖面插值后，声速改正精度得到提高，在波束入射角小于70°时水平位移误差小于0.1 m，水深误差小于0.15 m，满足多波束测量精度要求。

4 结论

本研究通过对常用三种声速剖面插值方法的实现难易程度、插值精度、适用性以及插值后的声速剖面对多波束声速改正的影响进行详细对比分析，得到以下结论：

1) 三种插值方法在一定程度上均可提高多波束声速改正精度；

2) 基于经验正交函数的声速剖面反演法插值精度高，适用性好，使用较少的参数即可表示声速与水深的复杂函数关系，便于声速场的构建；

3) 线性插值三角网法和反距离加权插值法算法简单，便于实现；线性插值三角网法对于三角网内的位置插值精度较反距离加权插值法高，但外推能力较差。

在实际工作中可根据具体情况选用某种插值方法，或综合使用。但值得注意的是，声速剖面插值只是对外业测量不足的一种补救措施，不应过于依赖。

[1]李家彪,郑玉龙,王小波，等.多波束测深及影响精度的主要因素[J]海洋测绘，2001(1)：26-32.

[2]阳凡林,韩李涛,王瑞富,等.多波束声纳水柱影像探测中底层水域目标的研究进展[J].山东科技大学学报(自然科学版),2013,32(6):75-83. YANG Fanlin,HAN Litao,WANG Ruifu,et al.Progress in object detection in middle and bottom-water based on multibeam water column image[J].Journal of Shandong University of Science and Technology(Natural Science),2013,32(6):75-83.

[3]周坚,周青,吕良,等.关于多波束声速剖面改正问题的探讨[J].海洋测绘,2014,34(4):62-65. ZHOU Jian,ZHOU Qing,LÜ Liang,et al.Discussion of multibeam sound velocity profile correction[J].Hydrographic Surveying and Charting,2014,34(4):62-65.

[4]GB 12327-1998.海道测量规范[S].

[5]S-44. IHO standards for hydrographic surveys[S].

[6]GENG X,ZIELINSKI A. New methods for precise acoustic bathymetry[J]. Processing of the Canadian Hydrographic Conference,1998:255-256.

[7]CARTWRIGHT D. Multibeam bathymetric surveys in the Fraser river delta,managing severe acoustic refraction issues[D]. Fredericton:University of New Brunswick,2003.

[8]关永贤,屈小娟.多波束测深中声速剖面的横向加密方法[J].海洋测绘,2009,29(5):54-56. GUAN Yongxian,QU Xiaojuan.The interpolation of sound velocity profile in horizontal plane in multibeam echosounding[J]. Hydrographic Surveying and Charting,2009,29(5):54-56.

[9]LEBLANC L R,MIDDLETON F H. An underwater acoustic sound velocity data model[J].Journal of the Acoustical Society of America,1980,67(6):2055-2062.

[10]沈远海,马远良,屠庆平. 声速剖面的分层经验正交函数表示[J].西北工业大学学报,2000,18(1):90-93. SHEN Yuanhai,MA Yuanliang,TU Qingping.On expression of ocean sound profile by layered empirical orthogonal function(EOF)[J].Journal of Northwestern Polytechnical University,2000,18(1):90-93.

[11]丁继胜,周兴华,唐秋华,等.多波束勘测声速剖面场的EOF表示方法[J].武汉大学学报:信息科学版,2007,32(5):446-449. DING Jisheng,ZHOU Xinghua,TANG Qiuhua,et al.Expression of multibeam echo sounding sound velocity profile with empirical orthogonal functions[J].Geomatics and Information Science of Wuhan University,2007,32(5):446-449.

[12]孙文川,暴景阳,金绍华.声速剖面EOF表示对多波束水深数据的影响研究[J].海洋测绘,2014,34(6):21-24. SUN Wenchuang,BAO Jingyang,JIN Shaohua.Effects of sound speed profiles represented by EOF to multibeam bathymetric data[J].Hydrographic Surveying and Charting,2014,34(6):21-24.

[13]成芳,陈爽,金绍华,等.陆缘深水区声速剖面EOF延拓方法研究[J].海洋测绘,2016,36(2):26-29. CHENG Fang,CHEN Shuang,JIN Shaohua,et al.An expanding method of sound velocity profiles via EOF in marginal deepwater areas[J].Hydrographic Surveying and Charting,2016,36(2):26-29.

[14]朱小辰,肖付民,刘雁春,等.表层声速对多波束测深影响的研究[J].海洋测绘,2007,27(2):23-25. ZHU Xiaochen,XIAO Fumin,LIU Yanchun,et al.Research on the influence of surface sound velocity in multibean echo sounding[J].Hydrographic Surveying and Charting,2007,27(2):23-25.

[15]顾春雷,杨漾,朱志春.几种建立DEM模型插值方法精度的交叉验证[J].测绘与空间地理信息,2011,34(5):99-102. GU Chunlei,YANG Yang,ZHU Zhichung.Accuracy cross-validation of several interpolation methods of DEM[J]. Geomatics & Spatial Information Technology,2011,34(5):99-102.

(责任编辑：高丽华)

Application of Sound Velocity Profile Interpolation Methods in Multibeam Echosounding

YAN Xunpen1,BU Xianhai1,LIU Hongxia1,XIN Mingzhen1,YANG Fanlin1,2

(1.College of Geomatics, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, National Administration of Surveying， Mapping and Geoinformation, Qingdao, Shandong 266590, China)

Because of the few and scattered distribution of sound velocity profile which is usually obtained by station measurement, it is very difficult to obtain sound velosity profile with enough density even by underway measurement. To solve this problem, the existing sound velocity profile were interpolated to meet the needs of sound velocity correction in this paper. The applicability and accuracy of three commonly used methods in sound velocity profile encryption of multibeam echosounding were discussed, namely, the inverse distance weighted interpolation method, triangulation with linear interpolation, and the sound velocity profile inversion method based on the empirical orthogonal function. Results show that all the three methods can improve the sound velocity correction accuracy. The sound velocity profile inversion method based on the empirical orthogonal function has highest accuracy and better applicability. Triangulation with linear interpolation has higher interpolation accuracy but poor extrapolating ability. Inverse distance weighted interpolation method is simple and easy to implement.

sound velocity profile interpolation; inverse distance weighted interpolation method; triangulation with linear interpolation; empirical orthogonal function(EOF)

2016-07-28

国家自然科学基金项目(41376108)；测绘公益性行业科研专项经费资助项目(201512034)；海洋公益性行业科研专项经费资助项目(201305034)

闫循鹏(1990—)，男，山东济宁人，硕士研究生，主要从事海洋测量方面的研究.E-mail:skdyxp@163.com 阳凡林(1974—)，男，湖北荆州人，教授，博士生导师，主要从事海洋测绘及GNSS应用等方面的研究，本文通信作者.E-mail:yang723@163.com

P229

文章编号：1672-3767(2017)02-0027-07