带有积分型边值条件的n阶边值问题正解的存在性和唯一性

武 晨

(江苏联合职业技术学院南京分院，江苏南京 210019)

带有积分型边值条件的n阶边值问题正解的存在性和唯一性

武 晨

(江苏联合职业技术学院南京分院，江苏南京 210019)

本文主要考虑一个如下的n阶边值问题

u(n)(t)+λf(t,u)=0,t∈(0,1).

边值条件为

其中，n≥2,λ为一个正参数。本文通过给出格林函数，利用复合单调算子定理得出上述边值问题的存在性、唯一性结果。

积分型边值条件；复合单调算子；格林函数

1 引言

非线性二阶多点边值问题正解的存在性因其广泛的物理意义引起了众多学者对其进行研究[1-8].孔令军[6]研究了如下更一般的带有积分型边值条件的二阶奇异边值问题：

其中，λ是一个正的参数，作者通过复合单调算子理论得到正解的存在性、唯一性结果.

众所周知，带有积分边界条件的边值问题不仅包含了两点、三点边值问题，而且可以更精确地描述许多重要的物理现象，如热传导、地下水流、化学工程等.对于带有积分型边值条件的二阶或者三阶边值问题已经有了很多结果，但对于带有积分型边值条件的高阶边值问题的研究结果相对较少.受以上文献的启发，笔者研究如下的n阶奇异边值问题：

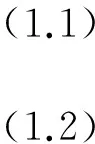
其中，n≥2,λ>0是一个正参数，f:(0,1)×(0,+)→[0,+)是连续函数，ξ(s)和η(s)非减，(1.2)中的积分是Riemann-Stieltjes型积分,非线性项f(t,x)允许在t=0,1和x=0时奇异.边值问题(1.1)(1.2)的正解，是指存在函数u∈C1[0,1]∩Cn(0,1)，使得当t∈(0,1)时有u(t)>0成立，且u(t)满足(1.1)和(1.2).

2 一些定义和引理

这里给出本文中需要用到的一些定义和引理，为了方便起见，定义如下记号：

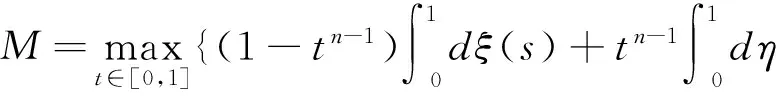
(2.1)

(2.2)

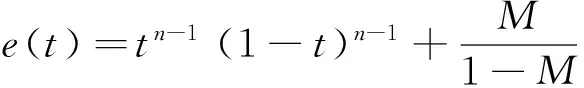
(2.3)

容易验证M≥m≥0.在本文中假设如下条件成立：

(H1)M<1；

(H3)f(t,x)=w(t)(g(x)+h(x))，其中w:(0,1)→[0,+∞)为连续函数，g:[0,+∞)→[0,+∞)为连续非减函数，h:(0,+∞)→[0,+∞)为连续非增函数；

(H4)存在α∈(0,1)，使得g,h满足：

g(kx)≥kαg(x).

(2.4)

h(k-1x)≥kαh(x).

(2.5)

而且当k∈(0,1)，x>0时，更进一步地满足：

(2.6)

对任意固定的λ>0，记常数Cλ>1，使得：

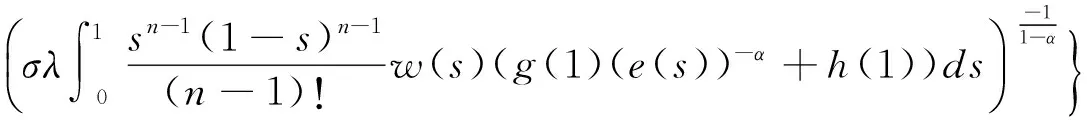
(2.7)

令

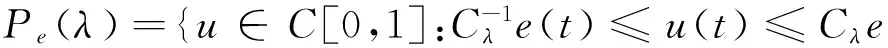
(2.8)

引理2.1[4]对任何y(t)∈C[0,1]，边值问题

有唯一解：

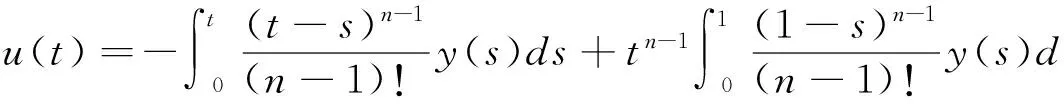
(2.9)

引理2.2[4]边值问题

对应的格林函数为：

(2.10)

且格林函数G(t,s)满足：

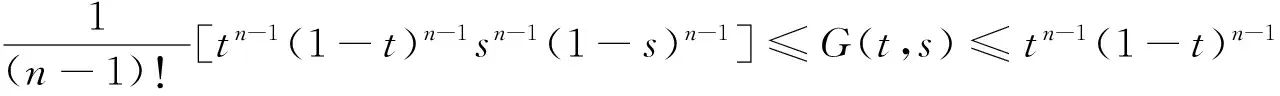
(2.11)

引理2.3 假设g∈L(0,1)，则方程u(n)(t)+g(t)=0,t∈(0,1)，对应边值问题(1.2)有唯一解：

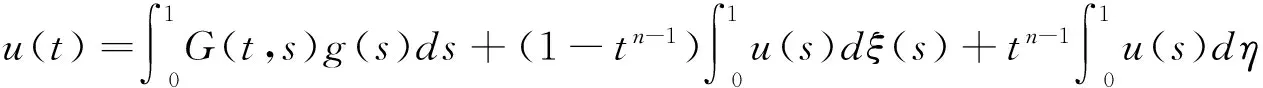
(2.12)

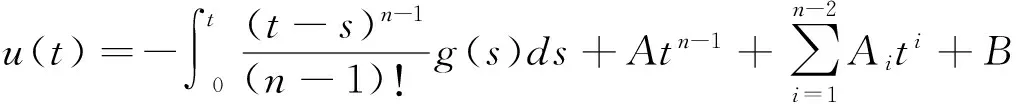
因此，该边值问题的唯一解可以表示为：

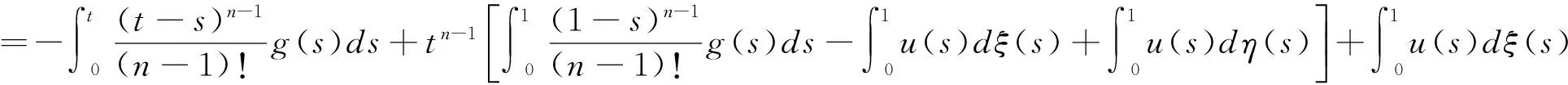
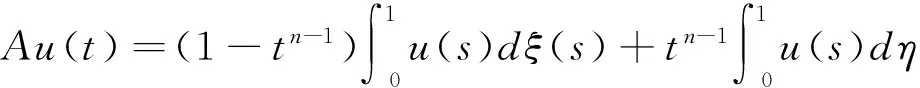
(2.13)

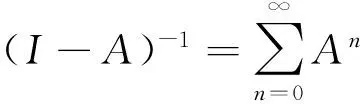
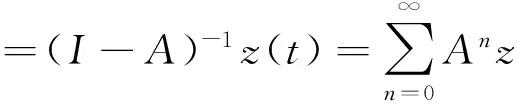
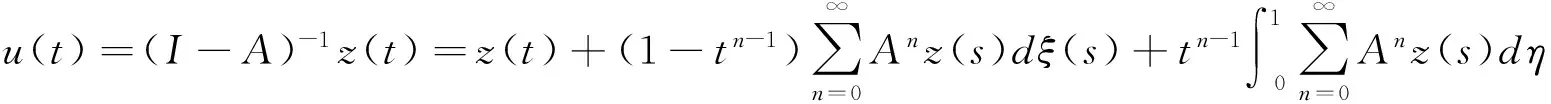
(2.14)

引理2.5 假设(H1)成立，对于u∈X，f(·,u(.))∈L(0,1),u(t)是边值问题(1.1)(1.2)的解,当且仅当u(t)是积分方程(2.14)的解.

为了证明定理，需要如下的复合单调算子的定义和引理.

定义2.1[7]假设T:Pe(λ)×Pe(λ)→Pe(λ)，则T(x,y)对于x是非减的，对于y是非增的，则称T(x,y)是一个复合单调算子，即对于x1,x2,y1,y2∈Pe(λ)，有x1≤x2,y1≥y2⟹T(x1,y1)≤T(x2,y2)，如果对于u∈Pe(λ)有T(u,u)=u成立，称u∈Pe(λ)是算子T的不动点.

引理2.6[7]假设T:Pe(λ)×Pe(λ)→Pe(λ)是一个复合单调算子，且存在α∈(0,1),使得T(ku,k-1v)≥kαT(u,v)，u,v∈Pe(λ)，k∈(0,1)，则T在Pe(λ)中有唯一的不动点.

3 主要结果

定理3.1 假设(H1)～(H4)成立，则对任何λ>0，边值问题(1.1)(1.2)在Pe(λ)中有唯一的正解uλ(t).

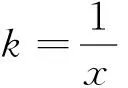
g(x)≤xαg(1),x≥1.

(3.1)

g(k)≥kαg(1),k∈(0,1).

(3.2)

在(2.5)中，分别令x=1，x=k，有：

h(k-1)≥kαh(1),k∈(0,1).

(3.3)

h(k)≤k-αh(1),k∈(0,1).

(3.4)

对任何λ>0，u,v∈Pe(λ)，定义算子T:Pe(λ)×Pe(λ)→X，有：

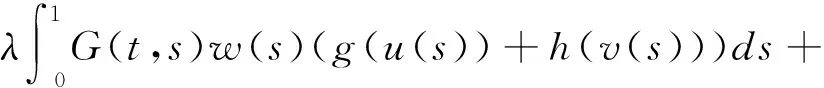
(3.5)

由(H3)中g和h的单调性可知,Tλ是复合单调算子.

接下来将证明T:Pe(λ)×Pe(λ)→Pe(λ).令u,v∈Pe(λ),t∈[0,1]，则由(2.11)(3.5)和引理2.5可知：

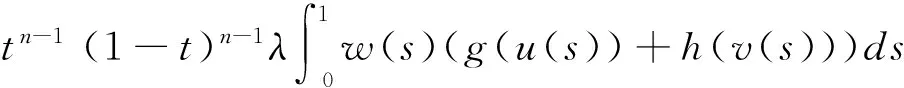
由(2.1)(2.3)可知，

由(3.1)(3.4)可知：

(3.6)

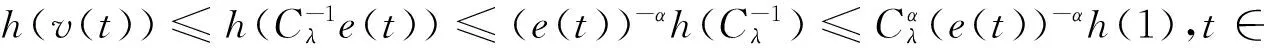
(3.7)

则由(2.7)(3.6)和(3.7)有：

(3.8)

另一方面，由(2.11)(3.5)可知：

(3.9)

对于s∈[0,1]，由(2.1)(2.2)(2.3)可知：

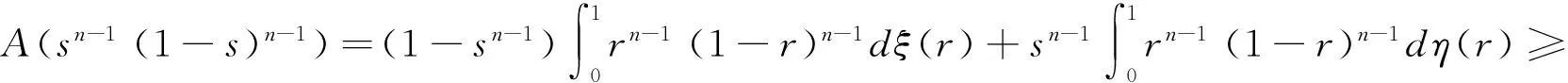
由数学归纳法可知：

An(sn-1(1-s)n-1)≥mn,n=2,3,…,s∈(0,1).

从而由(3.9)可知：

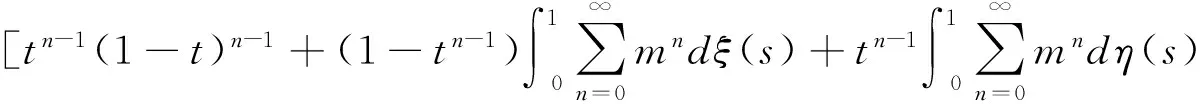
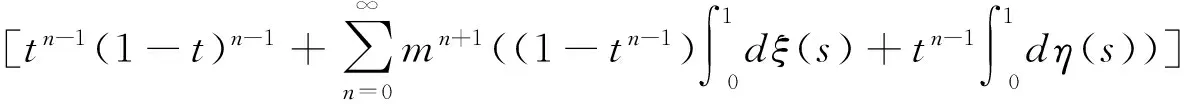
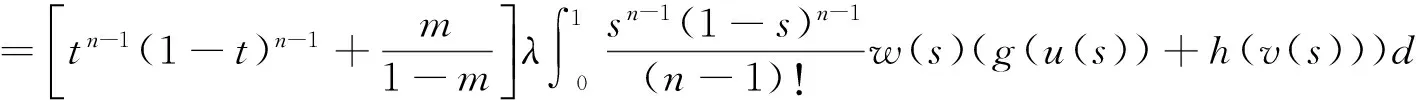
由条件(H2)可知：

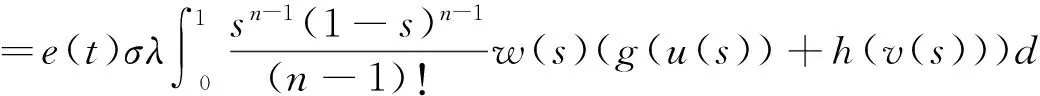
由(2.4)(3.2)和(3.3)，可知：

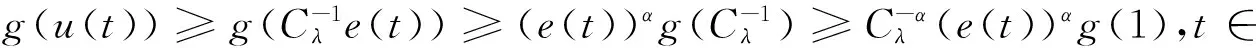
(3.10)

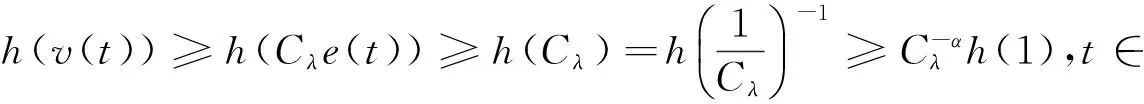
(3.11)

从而

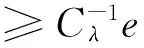
(3.12)

由(3.8)(3.12)可知，T(Pe(λ)×Pe(λ))⊆Pe(λ).

对任何u,v∈Pe(λ),t∈[0,1],k∈(0,1)，由(2.4)(2.5)和(3.5)有：

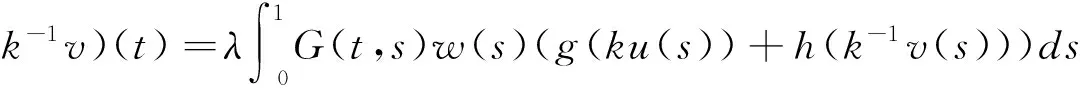
(3.13)

这样，引理2.6中所有条件就都满足了，由引理2.6可知存在唯一的不动点uλ∈Pe(λ)，使得Tλ(uλ,uλ)=uλ，由(H3)(3.6)和(3.7)可知：

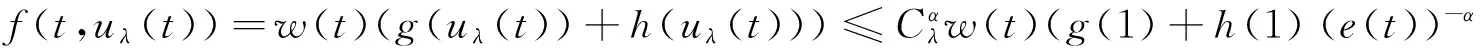
因此，f(·,uλ(.))∈L(0,1),由引理2.5可知，u(t)为边值问题(1.1)(1.2)的唯一解.容易验证uλ(t)>0，t∈(0,1)，即uλ(t)就是边值问题(1.1)(1.2)的唯一正解.

[1]Li Peiluan,Chen Haibo,Zhang Qi.Multiple positive solutions of n-point boundary value problems on the half-line in Banach spaces[J].Commun Nonlinear Simulat,2009(14):2909-2915.

[2]Liang Sihua,Zhang Jihui.Existence of countably many positive solutions of nth-order m-point boundary value problems[J].J.Comut.Appl.Math,2009(224):527-537.

[3]Eloe P W,Ahmad B.Positive solutions of a nonlinear nth-order boundary value problem with nonlocal conditions[J].Appl.Math.Letter,2005(18):521-527.

[4]Ji Yude,Guo Yanping.The existence of countabley many positive solutions for some nonlinear nth-order m-point boundary value problems[J].J.Comut.Appl.Math,2009(232):187-200.

[5]Liang Sihua,Zhang Jihui.The existence of countable many positive solutions for nonlinear singular m-point boundary value problems on the half-line[J].J.Comut.Appl.Math,2008(222):229-243.

[6]Kong Lingju.Second order singular boundary value problems with integral boundary conditions[J].Nonlinear Anal,2010(72):2628-2638.

[7]Zhang Zhitao,Wang Kelei.On fixed point theorems and mixed monotone operators and applications[J].Nonlinear Anal,2009(70):3279-3284.

[8]武晨.带有积分型边值条件的奇异的n阶边值问题无穷多正解的存在性[J].淮北师范大学学报:自然科学版,2015(36): 14-17.

The Existence and Uniqueness of Positive Solution for nth Order Boundary Value Problems With Integral Boundary Conditions

WU Chen

(Branch of Nanjing Jiangsu Union Technical Institute, Nanjing Jiangsu 210019,China)

integral boundary condition; mixed monotone operator; Green’s function

2016-04-19

武 晨(1985- )，男，讲师，硕士，从事微分方程研究。

O175

A

2095-7602(2017)02-0001-07