基于特征模型的高超声速飞行器再入多约束预测控制
张 军,李亚辉,朱晟桢
(1.江苏大学 电气信息工程学院,江苏 镇江 212013;2.中国运载火箭技术研究院,北京 100191)
基于特征模型的高超声速飞行器再入多约束预测控制
张 军1,李亚辉2,朱晟桢1
(1.江苏大学 电气信息工程学院,江苏 镇江 212013;2.中国运载火箭技术研究院,北京 100191)
针对存在输入和输出多约束的高超声速飞行器再入控制问题,提出了一种基于特征模型的鲁棒预测控制方法。对耦合的非线性再入动力学采用低阶线性特征模型简化,设计鲁棒预测控制器保证满足再入控制的多约束。基于特征模型的低阶等价性,将再入动力学的输入输出动态特性用线性时变的特征模型描述,并将三通道姿态耦合和干扰作为广义复合干扰。将灰色理论中累加求和的思想引入到特征模型参数辨识算法中,弱化了再入随机噪声的影响,通过灰色辨识方法在线估计特征模型的时变参数和干扰。设计一种基于线性矩阵不等式(LMI)滚动优化技术的H2/H∞鲁棒预测控制律与基于灰色辨识的补偿器共同构成复合控制器,保证了整个闭环系统的稳定,满足输入和输出约束。数据仿真验证了算法的有效性。
高超声速飞行器;约束;特征模型;鲁棒预测控制;灰色辨识
高超声速飞行器具有响应快速、机动能力强等特点,是未来国防装备的重要发展方向,其中再入控制系统设计最为复杂。在高超声速飞行器的再入过程中,运行环境复杂,飞行器飞行高度和飞行马赫数变化范围大,飞行器的气热特性、气动特性发生剧烈变化,造成再入动力学模型具有快时变、非线性耦合、强干扰等特性[1-2]。传统的PID控制很难使再入系统具有良好的闭环控制性能,这给再入控制器的设计带来了困难和挑战[3-4]。更值得注意的是,高超声速飞行器在再入过程中存在再入过程(动压、过载、热流)、执行结构等约束,导致姿态控制系统存在控制和状态等多约束,即舵机的偏角、气流系角、角速度等,违反了这些约束,再入控制系统性能和稳定性将受到严重的恶化[5-6]。
目前,动态逆控制、变结构控制、神经网络控制等方法提高了再入系统鲁棒性[7-9],但系统的输入和输出约束很少明确考虑。虽然采用高增益控制器的非线性控制和鲁棒控制能保证系统具有良好的闭环性能,却忽略了噪声放大和需要更大控制能力的问题[4],若考虑约束则原有的控制性能和稳定性就会受到破坏,控制律需要重新设计。目前,抗饱和控制方法、输入信号调节方法、预测控制等方法是解决约束控制的主要方法,文献[10]将抗饱和控制和输入参考信号调节2种方法组合起来有效解决输入约束,但是有一定的保守性,只有发生饱和行为时,抗饱和补偿器才执行,影响再入的高精度控制和强机动性能,并且不能处理输出约束。因此,需要在再入控制系统的高性能要求和满足约束之间进行有效折中。
预测控制具有反馈校正、模型预测、滚动优化等特点,能有效处理系统化多约束,逐渐被航天控制所关注[11-12]。文献[13]采用精确反馈线性化将再入非线性模型转化为线性模型,通过滚动优化机制解决再入飞行器的输入和输出约束,但是控制约束转化成非线性约束,计算仍然复杂,并且要求系统模型实时可逆。为了简化计算量,文献[14-15]在高超声速飞行器的上升段、再入段制导中设计了连续时变预测控制器,但没有考虑鲁棒性。预测模型是影响预测控制应用的关键因素,若把原有的多耦合、强非线性再入动力学模型直接作为预测模型,在线计算量很大,不能满足高实时性要求。文献[16]提出的特征模型用低阶线性单入单出时变差分方程来描述高超声速飞行器复杂动力学特性,形式简单,工程运行方便,对象特征模型与实际对象输出是等价的,在工程上得到成功应用。文献[17]设计了基于特征模型的自适应控制系统,采用了黄金分割控制律,分析了闭环系统的稳定性。文献[18]主要考虑飞行器平稳滑翔过程中滚动角保持为零的条件下,基于特征模型设计简化的自适应控制律。但是对于大角度再入机动的情况,偏航和滚动通道强耦合信息和非线性干扰不能简单忽略,再入特征模型需要考虑这一因素。
基于特征模型的低阶等价性,将再入动力学的动态特性用线性时变的特征模型描述,并把三通道姿态耦合和外来干扰作为广义复合干扰,对复杂的再入动力学进行简化建模。利用灰色预测中“累加生成”的优点,重新生成辨识数据,增强了辨识数据的规律性,通过灰色辨识在线估计特征模型的时变参数和干扰。在此基础上,设计H2/H∞混合预测控制指标,基于LMI滚动凸优化获得鲁棒预测控制律,保证了整个闭环系统的稳定,满足系统状态和输入约束。
1 再入飞行器动力学模型和问题描述
忽略地球自转、曲率、风、气动舵面等因素对飞行器动力学的影响,高超声速飞行器再入动力学模型为[4]
(1)
(2)
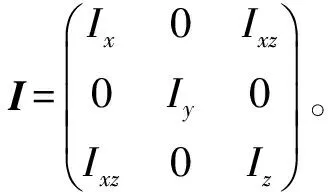
①舵偏角输入饱和约束。
|δa|≤δa,max,|δe|≤δe,max,|δr|≤δr,max。
②输出约束。
|α(k)|≤αmax,该约束保证了再入飞行器具有良好的气动特性和温度分布,降低了防热要求。
|ωx|≤ωx,max,|ωy|≤ωy,max,|ωz|≤ωz,max,角速度约束保证了飞行器的结构和力学安全要求。
再入姿态控制系统的任务是:在满足上述输入和输出约束的情况下,控制系统跟踪制导系统给出的攻角、滚动角指令,控制稳态精度小于0.5°,同时侧滑角保持为0。
2 再入动力学特征模型
再入动力学系统(1)和系统(2)是强非线性、时变、不确定的多变量耦合系统,直接设计控制器比较困难。基于文献[16]系统的特征模型输入输出等价原则,对系统(1)、系统(2)的控制输出α,β,φ求二阶导数,进行等价代换和泰勒级数近似展开,得到输入输出时变的二阶攻角离散模型:
α(k+1)=fα1(k)α(k)+fα2(k)α(k-1)+
g1(k)δα(k)+Δα(k)
fα1+fα2≈1,δα≈δe
(3)
β(k+1)=fβ1(k)β(k)+fβ2(k)β(k-1)+
g2(k)δβ(k)+Δβ(k)
fβ1+fβ2≈1,δβ≈δr
(4)
φ(k+1)=fφ1(k)φ(k)+fφ2(k)α(k-1)+
g3(k)δφ(k)+Δφ
fφ1+fφ2≈1,δφ≈δa
(5)
式中:fα1,fα2,g1为攻角通道的特征模型时变参数;δα,δβ,δφ为三通道的等效控制输入;fβ1,fβ2,g2为侧滑角通道的特征模型时变参数;fφ1,fφ2,g3为滚动角通道的特征模型时变参数。模型(3)~模型(5)是单入单出的时变系统,明显降低了原始再入动力学的复杂性。Δα(k)是攻角通道的广义扰动,包含其他特征通道的动态耦合信息、外部干扰,反映了再入飞行器的三通道强耦合、非线性、时变性,在飞行器大角度机动时该量不能忽略,这是与文献[16-17]的不同之处。定义:
Δα(k)=m11β(k)+m12φ(k)+Δα1(k)
(6)
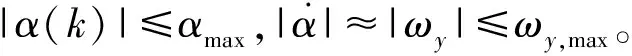
3 再入特征模型的灰色辨识
高超声速飞行器的再入特征模型是时变的单入单出系统,需要线辨识模型参数。而再入状态中含有近似均值为0的白噪声,影响辨识精度。目前,灰色预测的数据累加生成可有效弱化原始序列中随机噪声因素的影响,增强了数据的规律性,这里采用灰色辨识估计特征模型的参数fα1(k),fα2(k),g1(k),m11(k),m12(k),Δα1(k),具体步骤如下[18]。
(7)
进行一次累加生成(式中:m为采样数据数目),得到规律更强的新序列,消除随机噪声的影响,作为辨识的输入数据:
{X1(1),X1(2),…,X1(N)}
(8)式中:N为灰色序列数据数目,N≥n+1。由上述灰色数据定义得到再入动力学特征模型(3)的灰色模型为
(9)
在辨识时间内,建模误差和干扰近似认为
令V=(fα1(k)fα2(k)g1(k)m11m12Δα1)T,
(10)
由灰色模型可得:
(11)
为提高再入特征模型控制的鲁棒性,这里设计前馈补偿控制:
(12)
4 H2/H∞鲁棒预测控制
令Δfα1(k),Δfα2(k),Δg1(k)为特征模型系数辨识误差;Δ为uc(k)补偿Δα(k)后的误差,它们是有界的。此外,由于α(k),δα(k)也是明确的区域约束,因此,参数辨识误差、未建模动态、外界干扰等因素引起的综合扰动也是有界的,这里作为广义扰动,即
d(k)=Δfα1(k)α(k)+Δfα2(k)α(k-1)+
Δg1(k)δα(k)+Δ
灰色辨识补偿后的特征模型为
α(k+1)=fα1α(k)+fα2α(k-1)+g1δα1(k)+d(k)
δα=uc+δα1
(13)
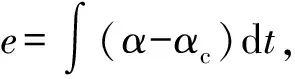
x(k+1)=A(k)x(k)+B(k)δα1(k)+Bdd(k)
(14)
对原有系统(1)的约束进行转化。
①攻角约束转化为系统(14)的输出约束:
|α(k)|=|(0 1 0)x(k)|≤αmax
②攻角变化率和飞行器最大角速度约束转化为系统(14)的输出约束:
(15)
式中:T为控制周期。
③考虑灰色估计补偿器后,新的输入约束:
u=|uc(k)+δα1(k)|≤δe,max
(16)
|δα1(k)|≤min(|δe,max-uc|,|-δe,max-uc|)=umax
(17)
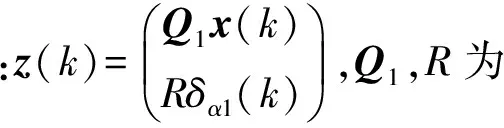
①H∞性能指标。对于任意给定的γ>0,从d(k)到z(k)的传递函数满足:
‖Gzd‖∞≤γ
(18)
②H2性能指标。
(19)
这里采用LMI设计控制器处理输入和输出约束,通过Lyapunov理论保证系统(14)的鲁棒性能和稳定性。基于H2/H∞性能指标提出如下定理。
定理1 设x(k)是系统(14)在采样k时刻的状态测量值,系统采用状态反馈控制律δα1(k+i)=K(k)x(k+i),F(k)=YQ-1,实现闭环系统鲁棒渐近稳定的充分条件是存在变量:b>0,Q>0,满足如下LMI多约束的优化问题:
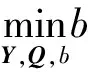
C1=(0 1 0)
证明 选取V(x(k))=xT(k)P(k)x(k),V(x(k+1))=xT(k+1)P(k)x(k+1),定义x(k+i)表示基于x(k)测量在k+i时刻的预测状态,δα1(k+i)是k时刻第i步预测控制,则控制系统的二次稳定需要满足:
(20)
由灰色辨识的收敛稳定性知道,补偿d(k)趋近于0,存在:
γ2dT(k+i)d(k+i)-zT(k+i)z(k+i)<0。
当M(k)<0时,V(x(k+i+1))-V(x(k+i))<0,当i=∞时,V(x(k+i))趋近于0,将式(20)左右两边从i=0到i=∞相加,得到:
(21)
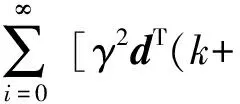
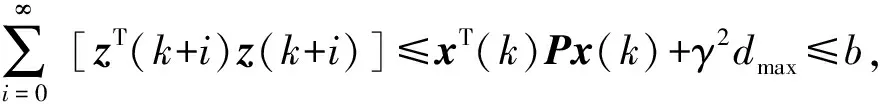
其中,M(k)<0是实现设计目标的充要条件。
(22)
利用Schur补性质,式(22)可以写成下面的矩阵不等式:
(23)
令Q=bP-1,K=YQ-1,对式(23)分别左乘、右乘diag{b1/2P-1,b1/2I,b1/2I,b1/2I,b1/2I},得到如下不等式:
(24)
H2性能指标式(19)等价如下LMI:
(25)
1)输出约束分析。
由M(k)<0,因此V(x(k+i+1))≤V(x(k+i)),推导zT(k)Q-1z(k)≤1 是不变集。
(26)
因为‖y(k+i|k)‖2≤ymax,所以
(27)
等价如下不等式:
(28)
因此,攻角约束转化为
(29)
角速度约束转化为
(30)
2)输入约束分析。
灰色前馈补偿后的舵偏角约束为
(31)
令K=YQ-1,则δα1=Kx=YQ-1x,不等式(31)可以写成如下的形式:
(32)
利用Schur补性质,式(32)等效如下的不等式:
(33)
3)算法实现。
本文提出的算法如下:
①基于实时的输入和输出数据,利用灰色辨识攻角通道的特征模型参数fα1,fα2,g1,m11,m12,Δα1(k)等;
②利用灰色辨识结果,设计补偿器uc补偿三通耦合运动信息、未建模信息和干扰Δα1(k);
③计算鲁棒预测控制律δα1=Kx,将总的控制u=δα1+uc施加到再入飞行器上;
④重复前面过程 ①。
其他通道控制算法与此类似。
5 仿真研究
针对某面对称的高超声速飞行器确定的飞行状态(αβφ)=(1000)(单位:(°)),获得相应的特征模型参数范围,设飞行器的高度为40 km,Ma=10,则其气动系数的范围如下[4]:
kxx∈[-0.358 5,-1.434 1],
kxz∈[-0.010 1,-0.015 2],
kyy∈[-0.106 0,-0.294 5],
kzx∈[-0.012 7,-0.050 6],
kzz∈[-0.025 3,-0.038 0],
kxa∈[40.590 9,34.339 5],
kxr∈[3.181 9,3.172 9],
kye∈[25.322 5,22.790 2],
kza∈[2.719 6,2.284 5],
kzr∈[4.536 3,4.133 8]。
假设飞行器姿态角速度的最大值为|ωx|max=|ωy|max=|ωz|max=1.047 rad/s,输入控制量最大值为30°,采样时间为0.01 s。
攻角控制通道:
α(k+1)=fα1α(k)+fα2α(k-1)+g1δα(k)+Δα,
fα1∈[1.996 8,2.003 2],
fα2∈[-1.003 2,-0.996 8],
g1∈[2.275 4×10-3,2.536 3×10-3]。
侧滑角控制通道:
β(k+1)=fβ1β(k)+fβ2β(k-1)+g2δβ(k)+Δβ,
fβ1∈[1.996 5,2.003 5],
fβ2∈[-1.003 5,-0.996 5],
g2∈[3.376 0×10-4,4.057 7×10-4]。
滚动角控制通道:
φ(k+1)=fφ1φ(k)+fφ2α(k-1)+g3δφ(k)+Δφ
fφ1∈[1.982 3,2.018 1],
fφ2∈[-1.018 1,-0.982 3],
g3∈[3.305 5×10-3,4.195 7×10-3]。
控制系统的要求为侧滑角保持在0°附近,攻角跟踪精度小于0.5°。
1)有时变扰动特征模型的攻角跟踪。
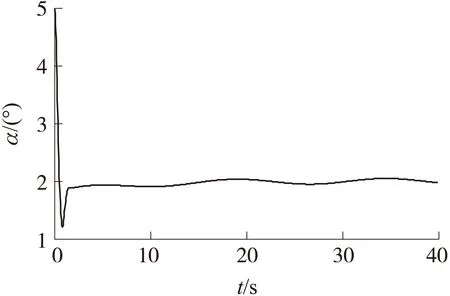
图1 时变干扰下的攻角跟踪曲线
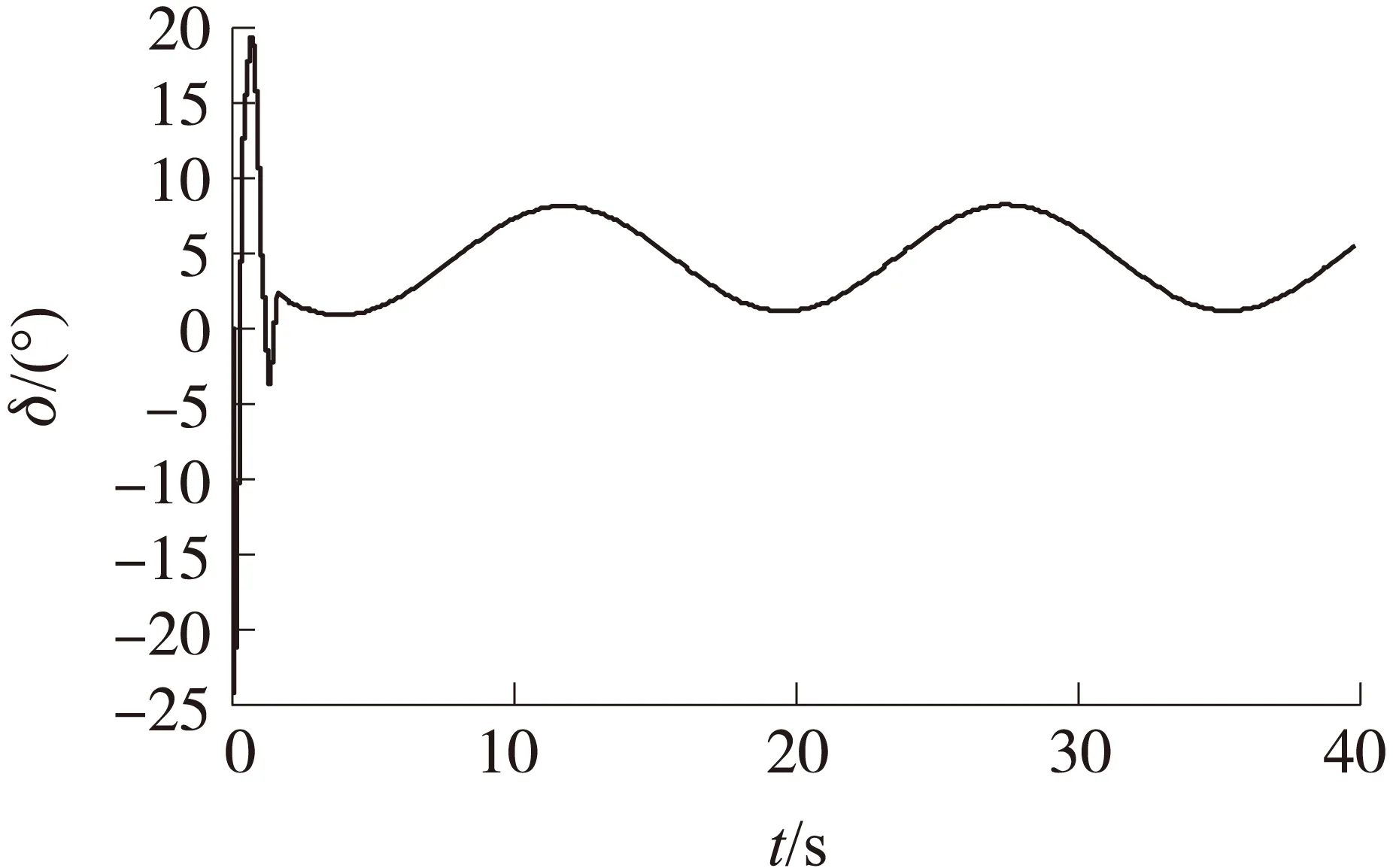
图2 时变干扰下的控制舵角曲线
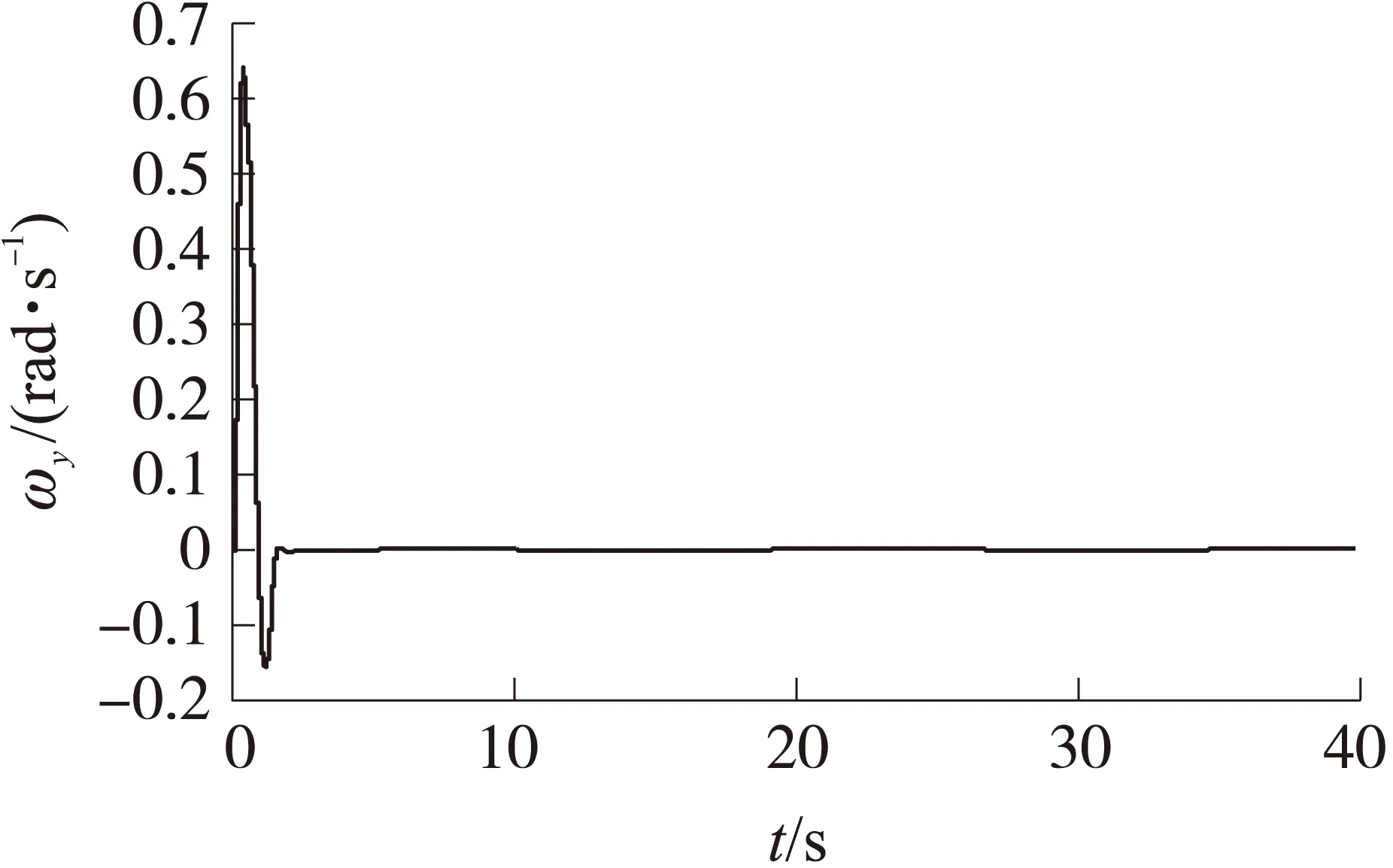
图3 时变干扰下的角速度曲线
2)随机噪声和时变扰动下的攻角跟踪。
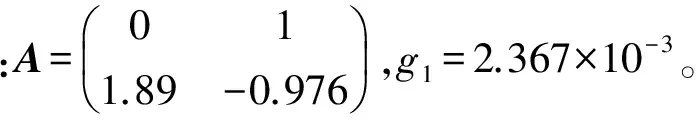
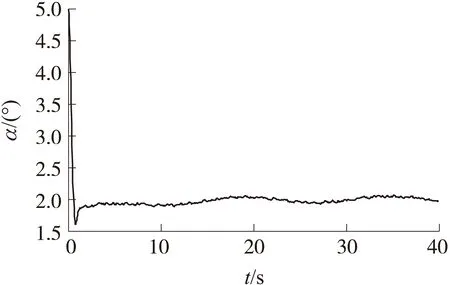
图4 随机噪声和时变扰动下的攻角跟踪曲线

图5 随机噪声和时变扰动下的控制舵角曲线
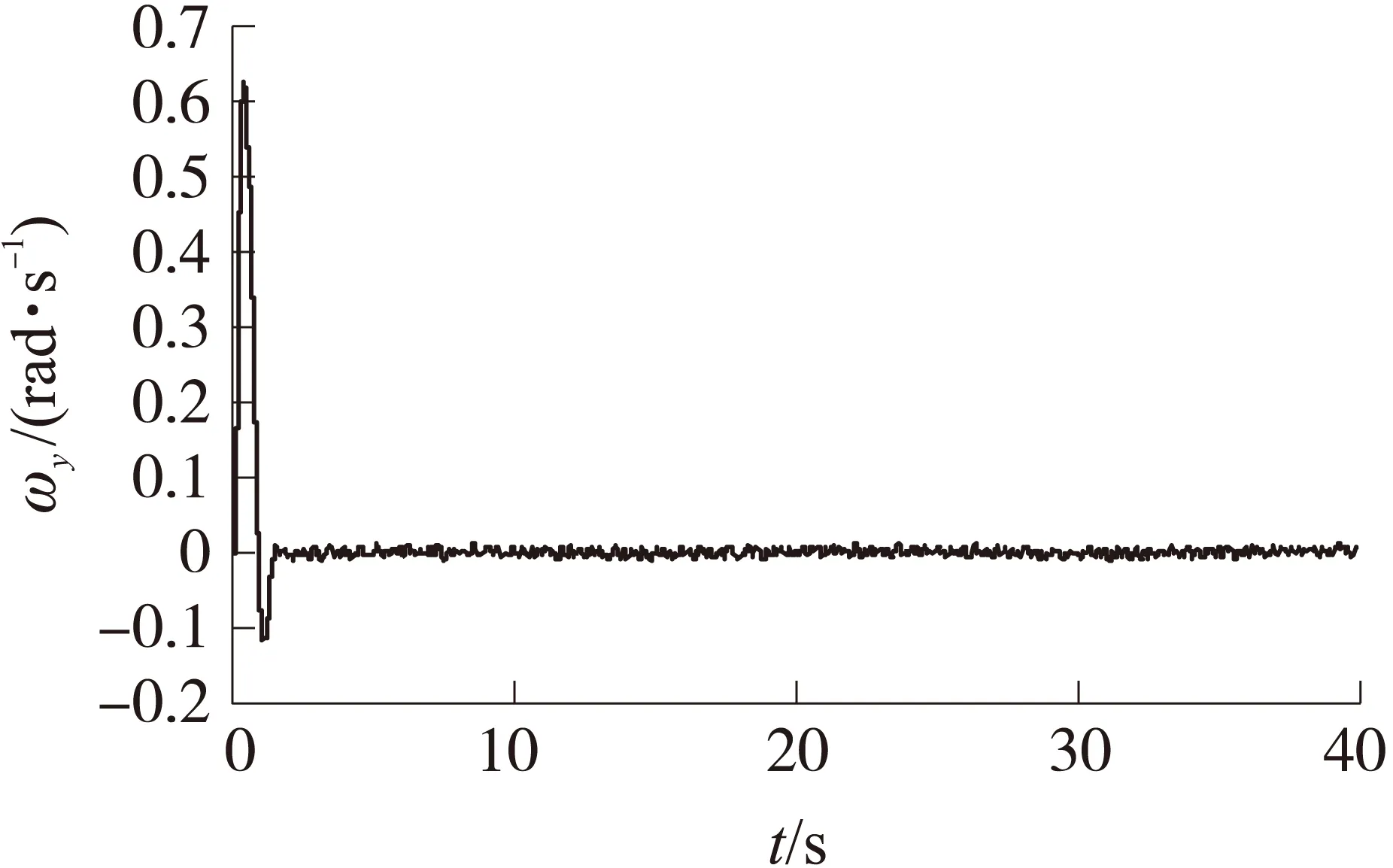
图6 随机噪声和时变扰动下的角速度曲线
6 结论
针对有输入和输出约束的非线性再入飞行器动力学模型,基于特征模型设计稳定的鲁棒预测控制律。采用时变的特征模型描述再入动力学模型,把三通道姿态耦合和外来干扰作为广义复合干扰,对复杂的再入动力学进行简化建模,并通过灰色辨识估计特征模型的时变参数;基于LMI滚动凸优化设计H2/H∞鲁棒预测控制律,保证了整个闭环系统的鲁棒稳定,满足系统的输入和输出多约束,通过数值仿真验证了本文算法的有效性。
[1] HARPOLD J.Shuttle entry guidance[J].Journal of the Astronautical Sciences,1979,28(3):239-268.
[2] LU P.Entry guidance:a unified method[J].Journal of Guidance,Control,and Dynamics,2014,37(3):713-728.
[3] WU H,MENG B.Review of the control research of hypersonic vehicle[J].Advances In Mechanics,2009,39(6):756-765.
[4] ZHANG Z,HU J.Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller[J].Science China:Information Sciences,2012,55(10):2 243-2 256.
[5] SHEN Z J,LU P.On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):111-121.
[6] LU P.Regulation about time-varying trajectories:precision entry guidance illustrated[J].Journal of Guidance,Control,and Dynamics,1999,22(6):784-790.
[7] XU B,SUN F,LIU H,REN J.Adaptive kriging controller design for hypersonic flight vehicle via back-stepping[J].IET Control Theory and Applications,2012,4(6):487-497.
[8] CHARLES E H,YURI B S.Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1 315-1 328.
[9] YURI B S,CHARLES E H.Reusable launch vehicle control in multiple-time scale sliding modes[J].Journal of Guidance,Control,and Dynamics,2000,23(6):1 013-1 020.
[10] ALICIA Z,ANDREA S.Combined reference governor and anti-windup design for constrained hypersonic vehicles models[C]//AIAA Guidance,Navigation,and Control Conference.New York:AIAA,2009:6 283-6 289.
[11] CHIRISTOPHER P,MORGAN B,ILYA K.Model predictive control guidance with extended command governor inner-loop flight control for hypersonic vehicles[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.New York:AIAA,2013:5 028-5 048.
[12] ZHANG J,SUN T R.Disturbance observer-based sliding manifold predictive control for reentry hypersonic vehicles with multi-constraint[J].Journal of Aerospace Engineering,2016,230(3):485-495.
[13] VAN W R.Combined feedback linearization and constrained model predictive control for entry flight[J].Journal of Guidance,Control,and Dynamics,2006,29(2):427-434.
[14] BRINDA V,DASGUPTA S.Guidance law for an air-breathing launch vehicle using predictive control concept[J].Journal of Guiance,Control,and Dynamics,2006,29(6):1 460-1464.
[15] WU H X,HU J,XIE Y C.Characteristic model-based all-coefficient adaptive control method and its applications[J].IEEE Transactions on Systems,Man,and Cybernetics-Prat C:Applications and Reviews,2007,37(2):213-221.
[16] XU L J.The hypersonic vehicle control based on the all-channel-coupled characteristic model[J].Aerospace Control and Application,2012,38(4):12-18.
[17] GONG Y L,WU H X.Characteristic model-based adaptive attitude control for hypersonic vehicle[J].Journal of Astronautics,2010,31(9):2 122-2 128.
[18] LIU L,CHEN R W.Modeling algorithm using accumulated generating operation and weighted product[J].System Engineering and Electronics,2010,32(5):976-979.
[19] PATIENCE E,ORUKPE I M.Model predictive control based on mixedH2/H∞control approach[C]//Proceedings of the 2007 American Control Conference.New York:IEEE,2007:11-13.
Predictive Control Based on Characteristic Model for Reentry Hypersonic Vehicle With Multiple Constraints
ZHANG Jun1,LI Ya-hui2,ZHU Sheng-zhen1
(1.Electrical and Information Engineering College,Jiangsu University,Zhenjiang 212013,China; 2.China Academy of Launch Vehicle Technology,Beijing 100191,China)
In order to study the reentry control problem of hypersonic vehicle with multiple constraints,a novel robust predictive-control-method was proposed based on the characteristic model.The low-order linear characteristic model was adopted to simplify the coupled nonlinear reentry dynamics,and the robust-predictive-controller was designed to satisfy the multiple constraints in the reentry control.Based on the low-order equivalence of characteristic model,the input and output dynamic-characteristic of the reentry dynamics was modeled by linear time-varying model,and the three-channel coupling and external disturbance were considered as a generalized composite disturbance.The accumulative sum idea in the grey theory was introduced into the parameter identification of characteristic model,and the effect of random noise factor was reduced,and the regularity of identification data was strengthened.The time-varying parameters and the disturbance were on-line estimated based on grey identification.The mixedH2/H∞robust predictive control-law was proposed by linear matrix inequality(LMI)receding horizon optimization technique,and the compensator of grey identification was feedforward compensated.The closed-loop system is stable,which satisfies the input and state constraints.The validity of the algorithm was verified by simulation results.
hypersonic vehicle;constraints;characteristic model;robust predictive control;gray identification
2016-08-19
国家自然科学基金项目(51379044;51405303;61503158)
张军(1972- ),男,副教授,博士,研究方向为飞行器控制,预测控制。E-mail:jzhang@ujs.edu.cn。
V249
A
1004-499X(2017)01-0001-08

