巧用对应思想 妙解计数问题

王荣峰

众所周知，学好数学离不开解题，而解题的一个核心思想就是将遇到的问题合理地转化为我们已经熟悉的问题，而对应就是实现这种转化的重要策略之一，下面就如何利用对应思想解计数问题加以盘点，以期能对大家解题能力的提升有所帮助.

1先分步再对应

评注该题并不复杂，可将所有“理想配集”逐个写出而获解，但不如借助分步计数原理先计算出自由元素2，4，6分配方式的种数再进行对应来解决更显简单.

2先分类再对应

例2从集合M=1，2，3，4，…，20中任取4个不同的元素，使这4个数构成等差数列，则不同的等差数列共有（ ）个.

A.57B.114C.171D.228

评注该题也可通过分类找规律的方法来解决，但将集合M按照被3除的余数分成三类，再巧妙进行对应，过程更简洁，当集合M中元素个数较多时，更看出该方法的优越性！

3先构建再对应

评注对于x1=0，通过在xii≤2≤10上加1可实现非负整数解到正整数解的转化，这为构建“隔板”这种模型创造了条件，再利用对应完成该题就是顺理成章的事了.

4先对应再对应

例4如图2所示的阴影部分由方格纸上3个小方格组成，我们称这样的图案为“L”形（每次旋转90°仍为L形图案），那么在由6×8个小方格组成的方格纸上可以画出不同位置的L形图案的个数是（）.

A.35B.48C.140D.980

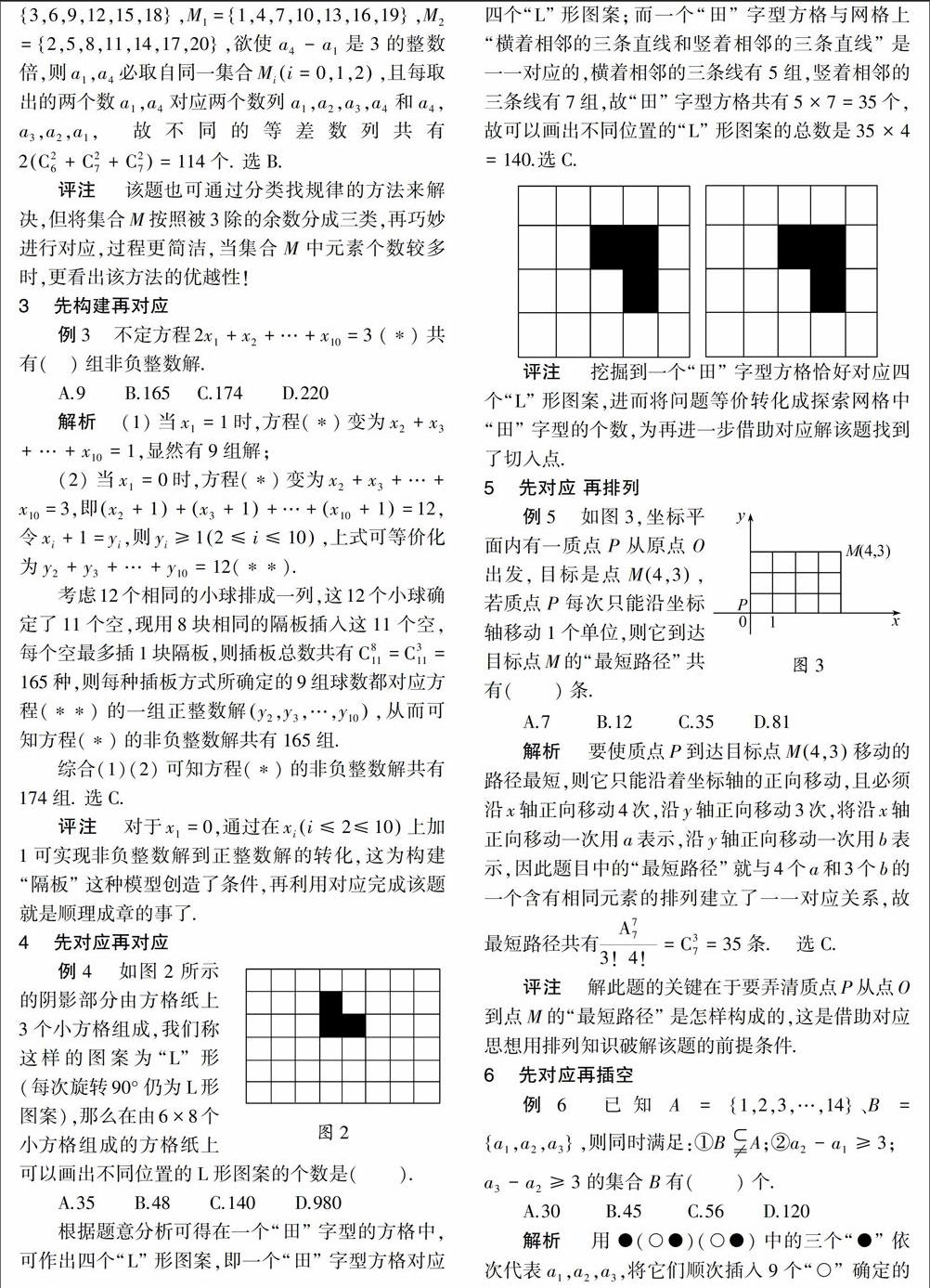
根据题意分析可得在一个“田”字型的方格中，可作出四个“L”形图案，即一个“田”字型方格对应四个“L”形图案；而一个“田”字型方格与网格上“横着相邻的三条直线和竖着相邻的三条直线”是一一对应的，横着相邻的三条线有5组，竖着相邻的三条线有7组，故“田”字型方格共有5×7=35个， 故可以画出不同位置的“L”形图案的总数是35×4=140.选C.

评注挖掘到一个“田”字型方格恰好对应四个“L”形图案，进而将问题等价转化成探索网格中“田”字型的个数，为再进一步借助对应解该题找到了切入点.

5先对应 再排列

例5如图3，坐标平面内有一质点P从原点O出发，目标是点M4，3，若质点P每次只能沿坐标轴移动1个单位，则它到达目标点M的“最短路径”共有（）条.

A.7 B.12 C.35D.81

评注解此题的关键在于要弄清质点P从点O到点M的“最短路径”是怎样构成的，这是借助对应思想用排列知识破解该题的前提条件.

6先对应再插空

评注该题难度较大，可以应用我们熟悉的“隔板法”来求解，但不如上述先对应，再插空，最后再排序独辟蹊径，解题过程令人耳目一新.

7先对应再选取

评注解该题的关键点是用0，1，2，…，r-1逐个加到ai1≤i≤r上，进而实现从“可重组合”到“无重复组合”的一一对应，为只需从集合B中选取r个元素就可巧妙解决该题做了重要铺垫！

“对应”作为一种数学思想和方法，在处理较难的计数问题中有着十分广泛的应用，用该方法解题的关键在于构造對应关系，但却没有通法可寻，只有平时勤于积累，善于总结，才能依据具体问题的特征进行分析，进而建模转化、合理对应，使问题顺利获解！